大展弦比太阳能无人机横航向姿态控制研究

王博,张贺,高正红

(1.西北工业大学 航空学院,陕西 西安 710072;2.航空工业第一飞机设计研究院,陕西 西安 710089)

太阳能无人机是近年来研究的新型飞行器。它通过太阳能电池板把光能转换成电能,以电机驱动螺旋桨提供动力,可连续留空飞行数月乃至数年之久。近10年来,太阳能无人机的飞行高度、续航时间等记录不断被刷新[1]。2018年7月,“Zephyr-S”无人机创造了26天不间断巡航的新记录[2]。高空巡航、低速、节能环保等特点[3-4]使太阳能无人机受到了美国、英国、瑞士、以色列等国家的强烈关注。较为著名的此类飞行器有:Helios、Aquila、Zephyr系列等[1]。国内方面,早在20世纪90年代,北京航空航天大学、南京航空航天大学、西北工业大学等高校就展开了太阳能无人机的持续探索。2002年,“绿色先锋”中国太阳能无人机探索研制计划启动[5]。2017年6月,由中国航天科技集团公司第十一研究院自主研发的新型彩虹太阳能无人机,在西北某地完成了20 km以上的临近空间飞行[6-7]。2019年西工大“魅影”太阳能无人机实现了27.6 h的连续飞行[8]。太阳能无人机的发展过程并不是一帆风顺。前期,由于对这类飞机的特性认识不足,研制过程中遭遇过多起飞行事故。Helios在2003年的燃料电池性能验证飞行时遭遇紊流,引发了严重的俯仰振荡而坠毁[9-10]。Aquila太阳能无人机在遇到强风时控制品质降低,被吹离航道,导致自动驾驶仪控制器强行压低俯仰姿态,并在飞机降落时加速,最终致使着陆失败[11]。

为追求高升阻比,增长留空时间,太阳能无人机采用大展弦比机翼、超低结构面密度设计来提高气动效率、能量效率。典型低速机翼的展弦比大于25,翼载约为常规飞机的1/10～1/4[12-13]。虽然翼展很大,但其质量和转动惯量较小。特殊的气动布局设计和质量特性,使其飞行动力学特性明显不同于常规飞机[14]。李锋等[15]分析了横航向气动特性,指出太阳能无人机交叉动导数较大,偏航阻尼导数较小。Ye等[16]建立了考虑风扰动的横航向线化动力学模型。张旺旺等[17]分析了3种翼型及2种布局形式的太阳能无人机的气动特性。

根据不同太阳能无人机的布局特点,有2类横航向姿态控制方法:基于副翼的控制策略和基于方向舵-发动机差动的控制策略。后者主要是解决较大动压下有可能出现的副翼反效问题。吴滔等[18]基于比例-积分-微分(PID)控制理论设计了协调转弯和平飞转弯2种控制方法。赵维娜等[19]基于PID的控制架构,采用伪逆法将控制效能分配到差动螺旋桨实现了横航向的姿态控制。马振宇等[20]针对全翼布局,采用线性自抗扰控制理论(LADRC),以方向舵和螺旋桨差动为控制输出,分别设计了滚转角控制器和偏航角控制器。

超大展弦比太阳能无人机飞行速度低、滚转阻尼导数大、偏航阻尼导数小,机翼上反变形直接影响气动特性,同时还存在空间运动耦合效应明显等问题。因此设计的横航向控制系统必须具有较好的鲁棒性。本文以30 m级翼展的太阳能无人机为研究对象,对比其与常规布局飞机的横航向气动特性差异,分析了横航向稳定性以及机翼变形对特征根的影响。采用基于Lyapunov判据的自适应反步法,设计了具有较强鲁棒性、适用于超大展弦比太阳能无人机的横航向姿态控制器。

1 飞机布局及气动特性分析

1.1 气动特性分析

太阳能无人机气动布局如图1所示,采用上单翼和H型尾翼。机翼中间段为大展弦比平直翼,外翼段采用梯形设计,具有6°上反角。整个机翼采用同一种翼型。翼展接近30 m,翼下挂载4个短舱。机身由流线型机头、四边形截面前机身、三角形截面中机身和后机身组成。

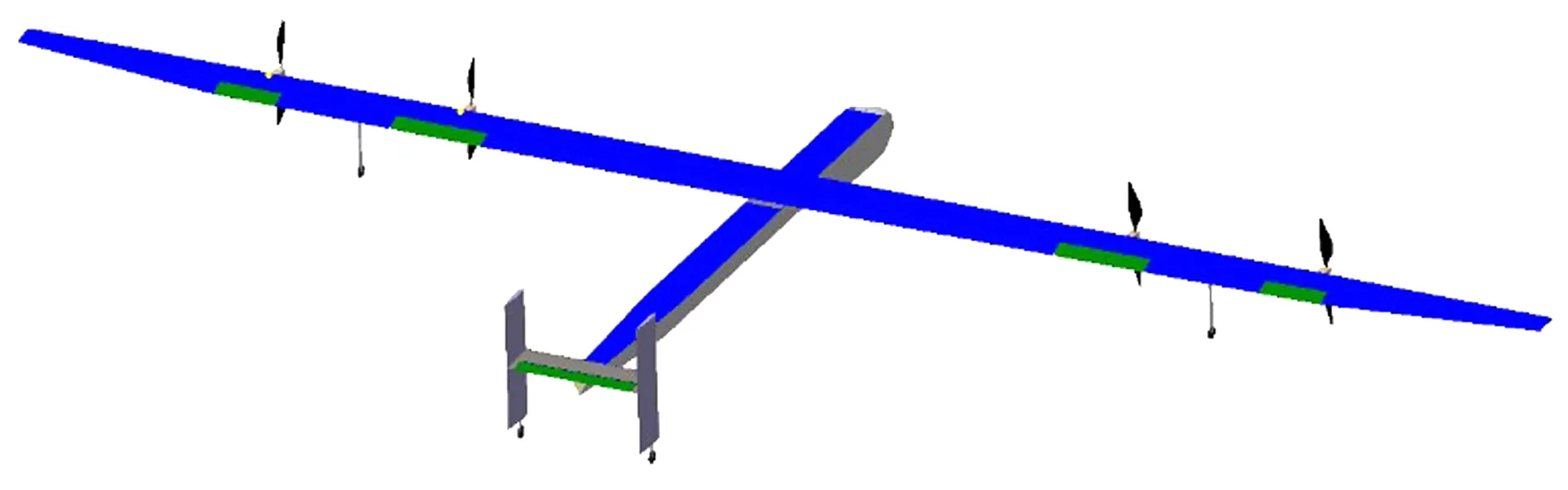
图1 太阳能无人机气动布局

采用CFD软件计算了0°迎角时,滚转力矩系数、偏航力矩系数和横向力系数随侧滑角的变化曲线,如图2～4所示。由图可以看出,在0°～15°的侧滑角范围内Cl-β,Cn-β和Cy-β均保持良好的线性关系。航向静稳定导数Cnβ为0.001 5。横向静稳定导数Clβ为-0.001 7。这表明该气动布局具有良好的横航向静稳定性。

按质量划分,30 m级太阳能无人机属于“轻小类”飞机(Ⅰ类)。但机翼作为重要气动部件,其尺寸又接近大型“轰运类”飞机(Ⅲ类)。为了不失一般性,表1分别列举了太阳能无人机、常规Ⅰ类飞机和Ⅲ类飞机的横航向气动导数。通过对比可以看出,太阳能无人机横向力系数对侧滑角的导数CYβ,航向静稳定导数Cnβ与Ⅰ类飞机接近,但仅是Ⅲ类飞机的1/2。滚转阻尼导数Clp和滚转角速率引起的交叉动导数Cnp均大于Ⅰ类和Ⅲ类飞机。偏航角速率引起的交叉动导数Clr是Ⅰ类飞机的2倍,与Ⅲ类飞机接近。偏航阻尼导数Cnr是Ⅰ类飞机的1/4～1/3。

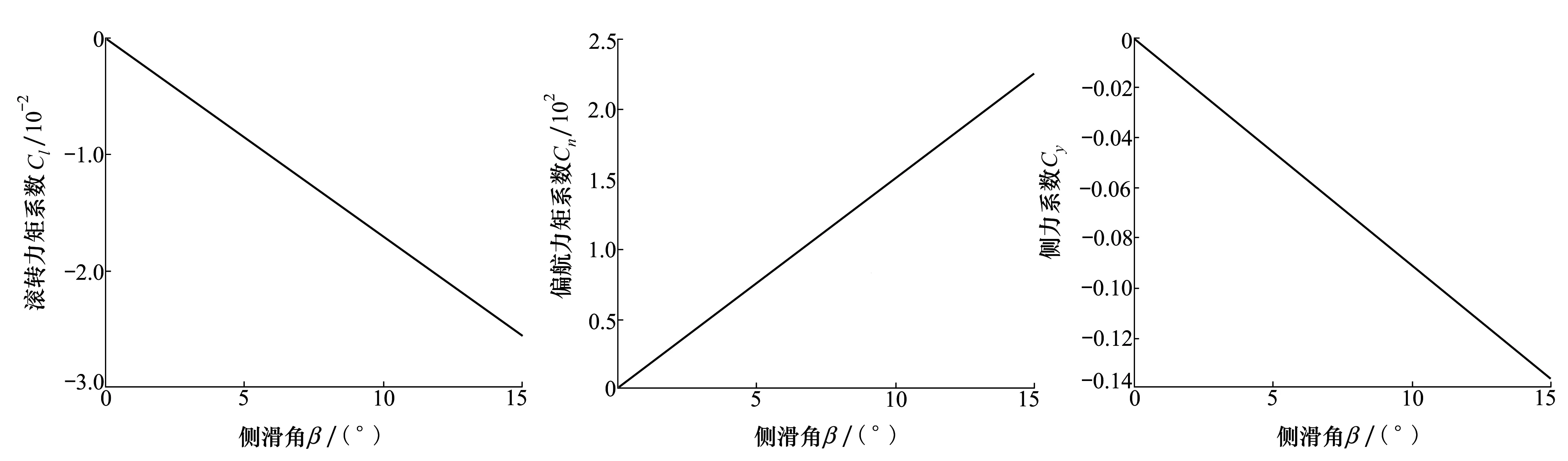
图2 滚转力矩系数 图3 偏航力矩系数图4 横向力系数

太阳能无人机特殊的横航向气动特性是由其气动布局决定的。外翼安装角以及机翼上反变形,导致了较强的横向静稳定性。超大的机翼展长,导致滚转阻尼导数较大。飞机垂尾力臂相对较短,尾容量小,使得航向静稳定导数和偏航阻尼导数较小,航向动稳定性稍差,需要在控制律设计时增加角速率反馈,改善阻尼特性。

表1 横航向气动导数对比

1.2 动力学导数对比分析

表2 飞机惯量对比 kg·m2

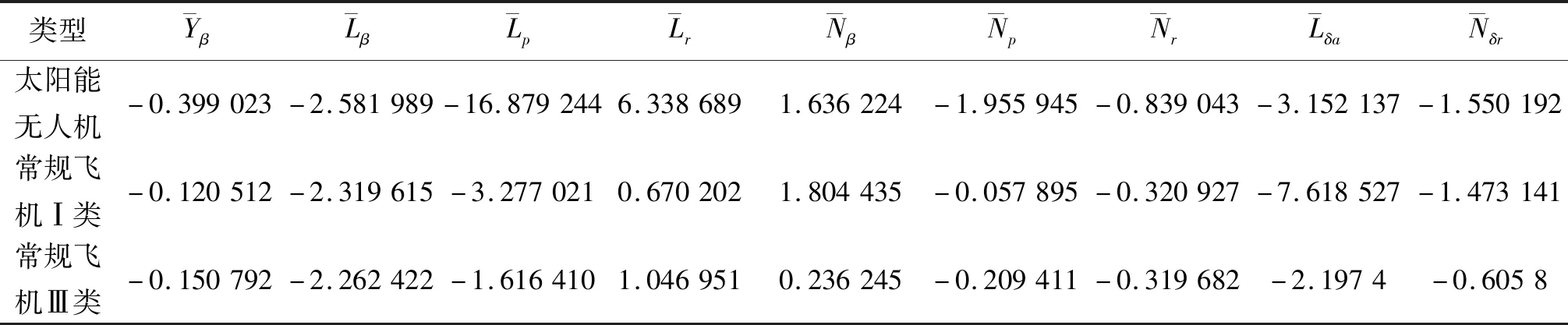
表3 飞机动力学导数对比 rad-1

1.3 机翼上反变形的影响分析

由于太阳能无人机的翼展和面积较大,加之结构刚度弱,容易受到大气扰动或机动过载的影响,产生较大的弹性变形。Britt等[21]在风洞试验中发现柔性机翼的最大变形可达翼展的50%。静强度分析表明,30 m级翼展的太阳能无人机在低空巡航状态,翼尖变形位移为1.2 m。当承受限制载荷时,翼尖的最大变形位移可达3.6 m。相对于未变形状态几何差异较大,如图5所示。与之对应的是上反角变化,平飞时飞机上反角约为7.2°,在极限载荷情况下飞机上反角变为19.8°。

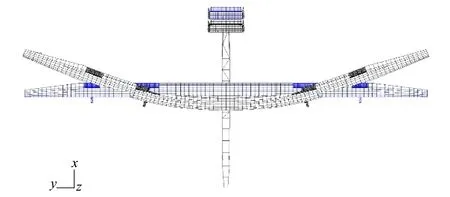
图5 太阳能无人机机翼变形

上反角的变化会对太阳能无人机的横向特性产生较大影响。考虑右侧滑的情况，来流速度矢量V分解为迎面气流分速度Vx=Vcosβ和横向气流分速度Vy=Vsinβ。再将横向气流分速度Vy沿翼面和垂直于翼面的方向分解。垂直于翼面的分速度为

Vn=±Vsinβsinφ

(1)

式中，φ为上反角。在右侧,Vn向上为正值,导致右半翼迎角增加,变化量为

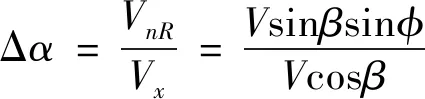
(2)

单侧机翼升力增加引起的滚转力矩系数可表示为

(3)

由(3)式可见,正侧滑产生负的滚转力矩,且与飞机的上反角φ成正比[22]。按照公式(3)估算,在承受极限载荷情况下,太阳能无人机上反角的增大将引起横向静稳定性力矩系数增大约3倍。与之相关的滚转模态、荷兰滚模态以及螺旋模态特征根都将发生较大变化。同时,产生同样滚转角速率所需的副翼偏度将增大。

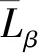
(4)

2 横航向运动特性分析

2.1 模态特性

为了评估太阳能无人机的横航向模态特性和受上反角以及惯量变化的影响,分别计算特征根随速度和机翼上反角的变化。考虑到该类飞机的速度范围很窄,选择的计算条件为:高度3 000 m,速度在12～20 m/s(当量空速)的范围内变化。机翼上反角变化范围为从平飞变形到最大过载变形。假设机翼的上反角变化与翼尖变形位移为线性关系。图6显示了特征根随速度以及机翼上反角变化的趋势。随着速度的增大,荷兰滚模态的频率增加,阻尼减小。滚转模态与螺旋模态的特征根则向左平面移动。荷兰滚模态的特征根随上反角变化的趋势与随速度变化的趋势一致,但移动较快。

图6 横航向根轨迹变化

由图6可以看出,太阳能无人机具有较大的滚转模态和荷兰滚模态特征根。其横航向模态响应较快,满足一级品质,但螺旋模态不稳定。根据经典理论,保留特征方程中的线性项和常数项,得到螺旋模态特征根的近似估算公式。

(5)

一般情况下分母大于零,所以(5)式的正负由分子决定，故螺旋模态的稳定条件为

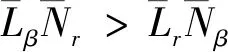
(6)

2.2 姿态安全边界

(7)

由于飞机运动是复杂的空间运动,副翼是否能够稳定飞机的滚转,不仅与操纵舵效相关,还受空间姿态影响。根据欧拉角的形成过程,存在(8)式运动学关系

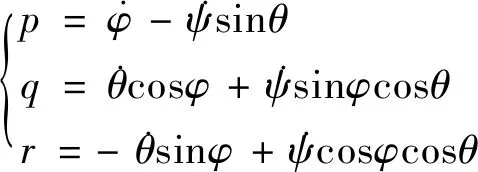
(8)

式中,p,q,r分别是滚转角速率、俯仰角速率和偏航角速率;φ,θ,ψ分别是滚转角,俯仰角和偏航角。

(9)

求解公式(9)可以得到不同速度条件下,稳定转弯过程中,滚转角与俯仰角的对应关系

(10)

将副翼最大偏度以及气动数据代入(10)式,可获得不同速度条件下,受副翼效率限制的滚转姿态安全边界,如图7所示。

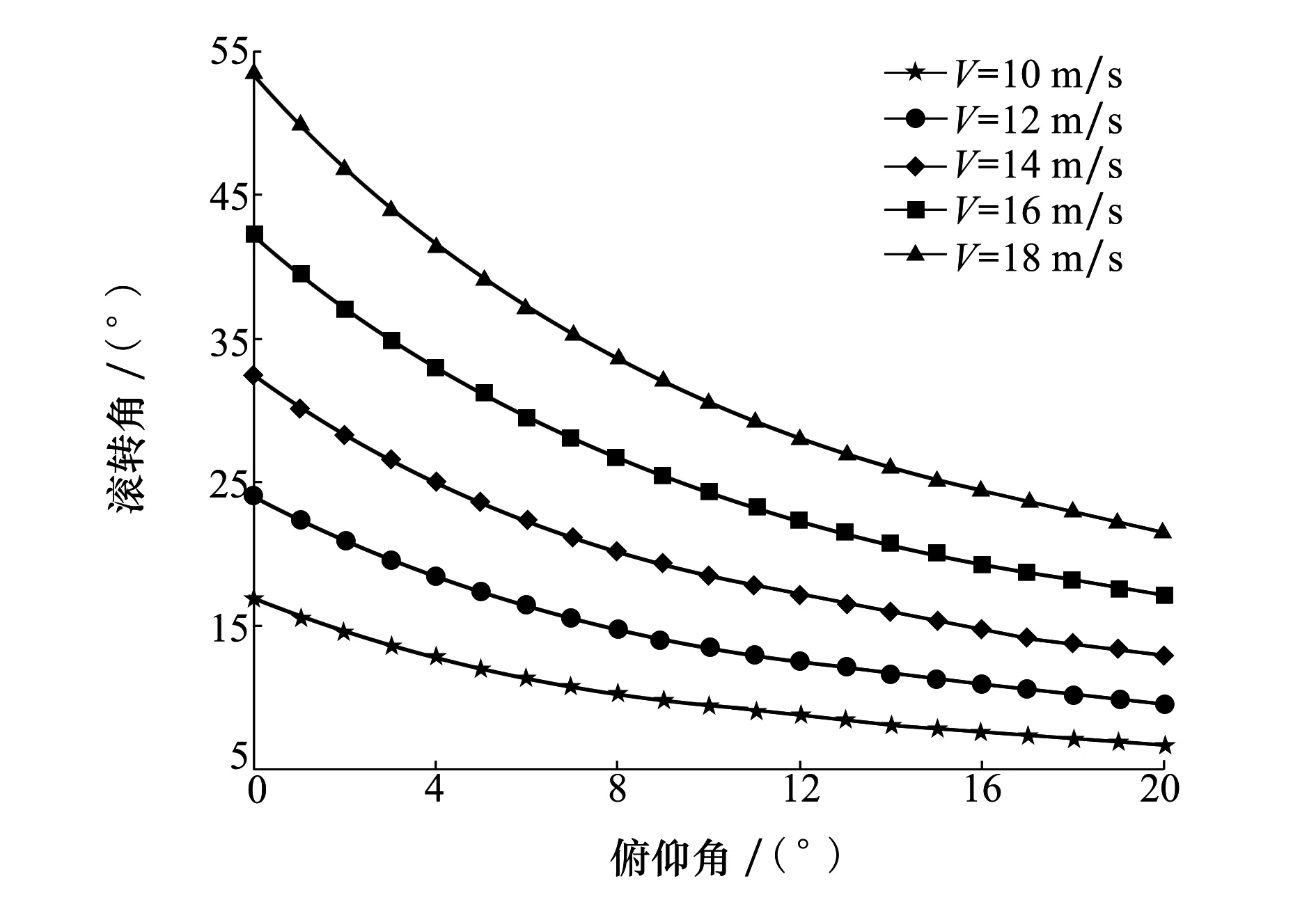
图7 姿态角限制包线

随着俯仰角的增大,滚转姿态安全边界逐渐减小。随着速度的增大,滚转姿态安全边界逐渐增大。对于常规飞机,稳定运动基本不受姿态影响,设计姿态保护功能是为了防止飞行员出现空间迷失或无意识地进入危险状态。但对于太阳能无人机,姿态会影响运动稳定。当飞机处于姿态限制边界时,飞机改平困难。表现为飞机的滚转不跟随指令。飞机超出姿态边界时,会导致飞机的滚转角持续增大。图8仿真了飞机配平在2°俯仰角,受到10°初始滚转扰动后的响应过程。初始时,由于螺旋模态不稳定,滚转角持续增大。在第3 s时,滚转角达到15°,偏航角速率达到8°/s。此时已超过安全姿态包线。反向满偏副翼后虽然减缓了滚转角的增长趋势,但仍不能阻止飞机的持续滚转。因此,应严格限制太阳能无人机的滚转姿态和偏航角速率。

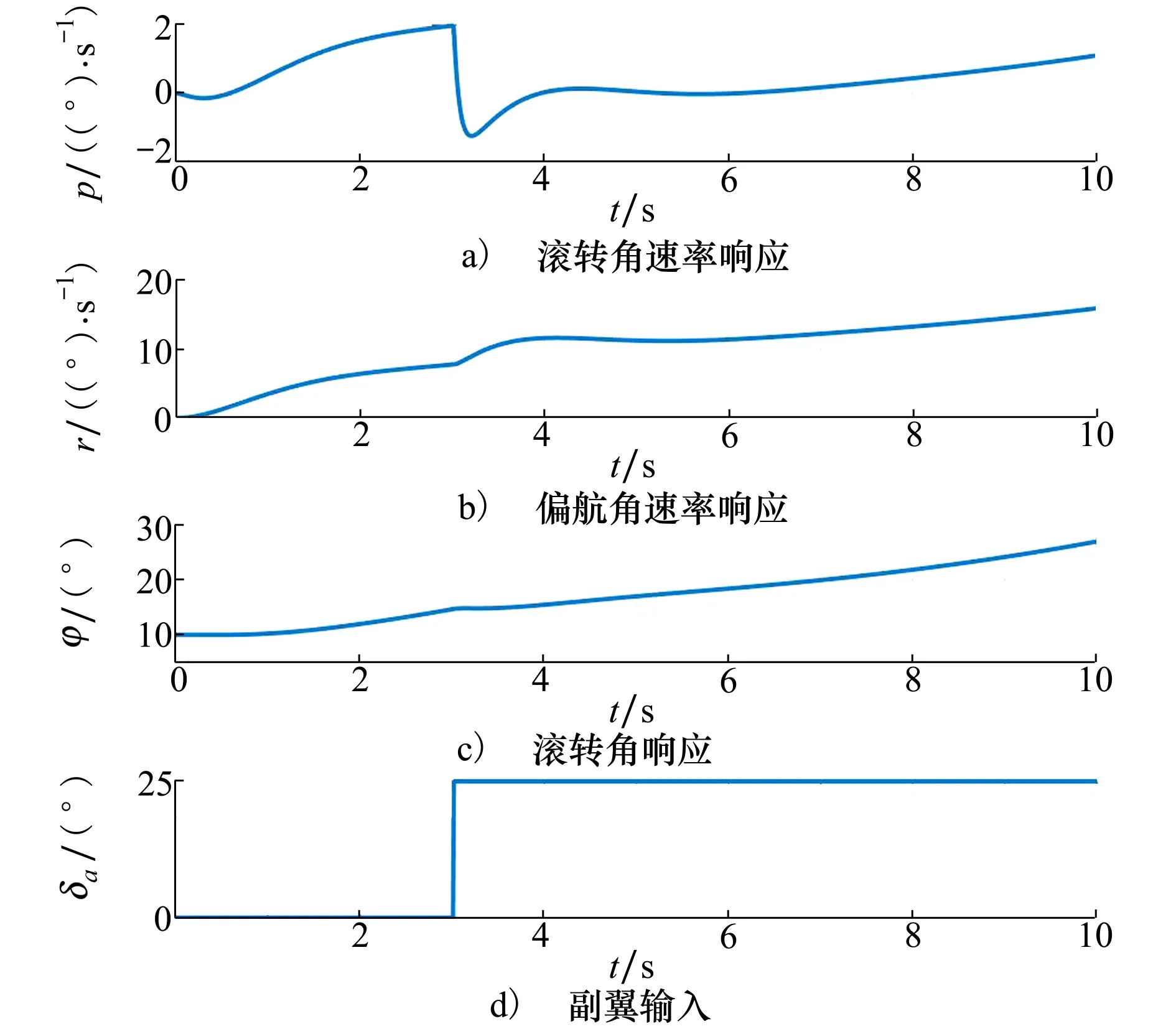
图8 滚转角发散仿真

3 自适应反步法控制律设计

传统无人机控制一般采用PID方法,姿态控制作为外环,角速率控制作为内环,如公式(11)所示。其中,ay是侧向加速度,用于改善荷兰滚频率,W(s)是高通滤波器,用于滤出偏航角速率高频信号增加荷兰滚阻尼。

(11)

(11)式的控制结构忽略了耦合项的影响,这会导致滚转姿态控制产生较大的超调和稳态误差,如图9所示。这对于稳定性受姿态影响较大的太阳能无人机来说,存在安全风险。尤其在遭遇紊流时,容易超出姿态安全边界。针对太阳能无人机需要在小姿态包线范围内缓慢精确控制的要求,本文提出利用自适应反步法设计横航向控制律。

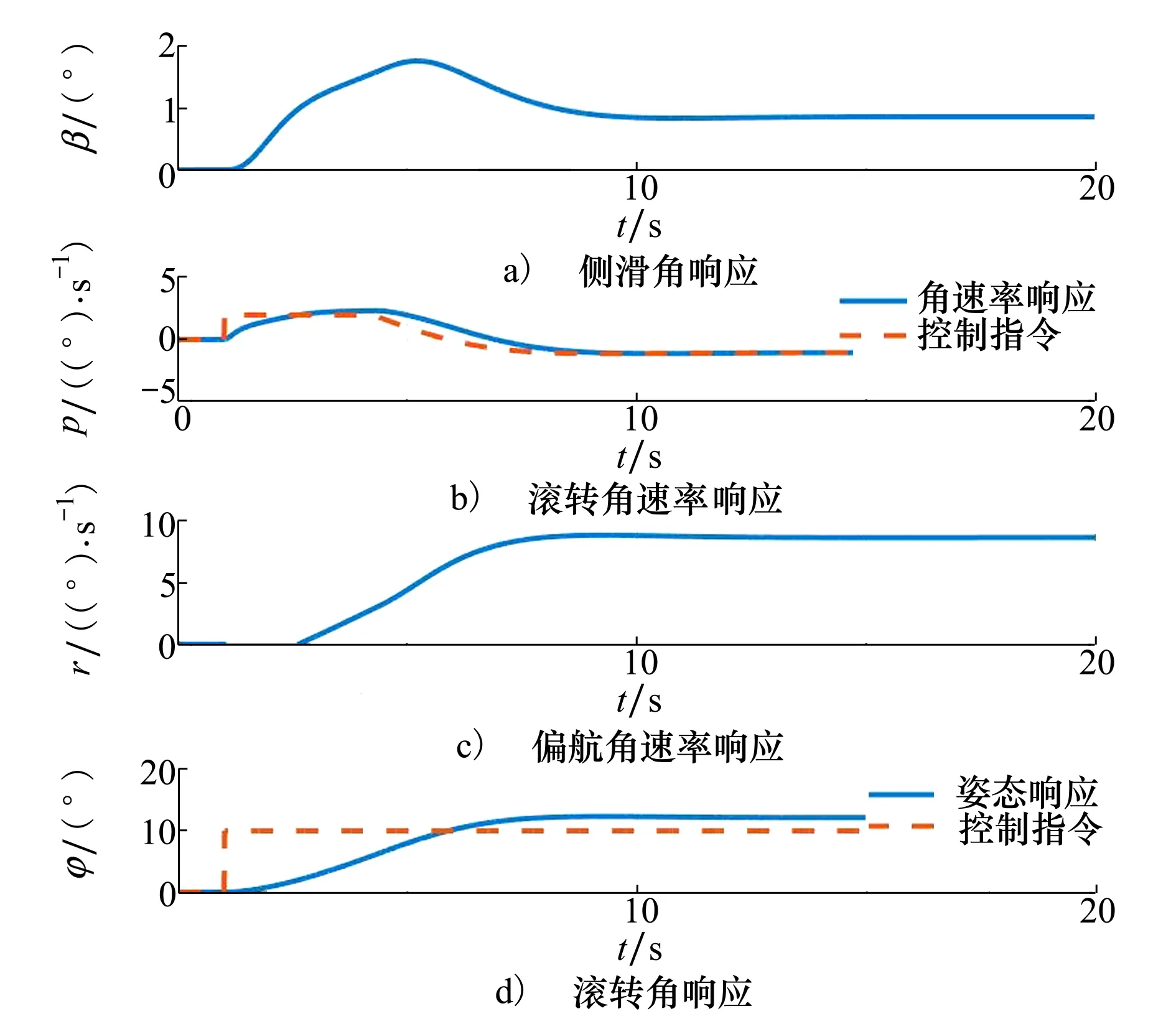
图9 滚转角PID控制稳态误差

自适应反步法是基于Lyapunov直接法获得的控制结构,具有结构简单、适应性广和鲁棒性强的特点[23-26]。具体来说,引入“时标分离”理论,根据被控状态响应的快慢进行分类,然后分别控制。响应快的设置为“快回路”,响应慢的设置为“慢回路”。太阳能无人机的滚转角、侧滑角相对于滚转角速率、偏航角速率为慢变量。同时,侧滑角对横航向特性有重要影响,转弯过程中侧滑不能太大。因此选取φref,βref作为外环控制变量。选取滚转角速率pref和偏航角速率rref作为内环控制变量。自适应反步法控制律设计过程如下。

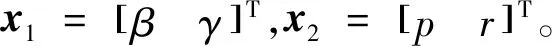
整理形成方便使用反步方法的严格反馈形式

(12)

式中:fβφ,gβφ,fpr,gpr为非线性方程系数。

根据公式(12)定义Lyapunov函数V1

(13)

两边求导,并整理得

(14)

为了满足Lyapunov稳定条件,定义矩阵元素均为正值的对角阵k1,k2,使得

(15)

解得控制律为

(16)

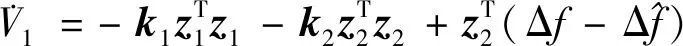
(17)

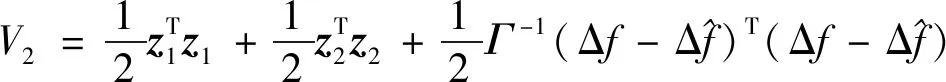
(18)

假设建模误差Δf不随时间变化,对公式(18)两边求导得

(19)

将公式(16)～(17)代入可得

(20)

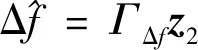
(21)

根据公式(16)和(21)设计的太阳能无人机自适应反步法控制律结构如图10所示。外环采用φref,βref角度控制,经反步法解算形成滚转角速率、偏航角速率虚拟控制量pref,rref。在内环角速率控制反步法解算中引入自适应律(21),并形成最终副翼和方向舵指令。

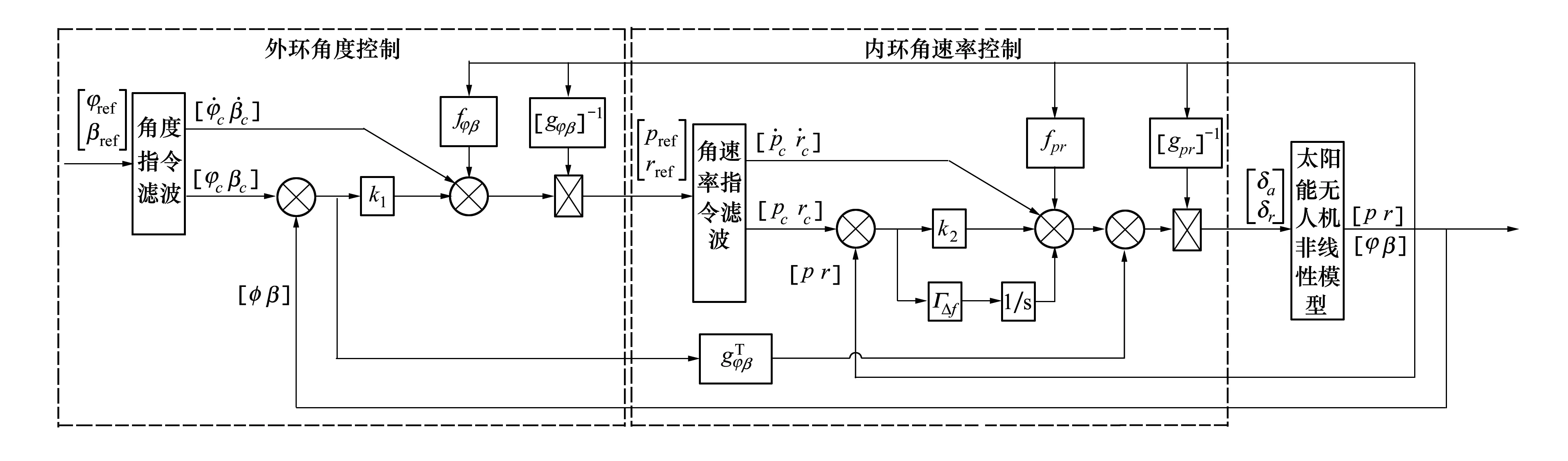
图10 自适应反步法控制律

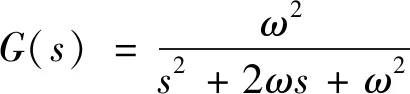
(22)

4 试验验证

4.1 仿真验证

采用无人机六自由度非线性数学模型,对基于自适应反步法的横航向姿态控制律进行仿真验证。首先将飞机配平在飞行高度3 000 m,速度16 m/s的巡航状态,输入阶跃的滚转角控制指令和零度侧滑角指令。进一步,为了验证自适应反步法的鲁棒性,根据上反角的变化将飞机横向静稳定导数Clβ增大2.7倍,将惯性矩Ixx增大约1.4倍,再次进行仿真,并将结果与PID方法的控制效果进行对比。

仿真结果如图11～12所示。通过对比分析可以看出,如果不考虑机翼上反变形影响,自适应反步法与PID方法均能达到较好的控制效果,实现了对滚转角指令的精确跟踪。最大滚转角速率和偏航角速率约为2°/s。但自适应反步法改变了侧滑角的响应形态,减小了侧滑振荡。当在飞机模型中引入上反角变化影响后,控制效果差异明显。自适应反步法仍能实现对滚转角的精确控制,稳态误差为零,且各个状态量的动态响应过程与刚体飞机响应基本一致。受横向静稳定性系数增大影响,仅滚转角速率响应过程稍微变缓。在PID控制中,滚转角响应上升时间由3.15 s增加到4.53 s,出现了明显的超调,超调量为15.6%。同时滚转角速率、偏航角速率响应振荡明显。因此,自适应反步法更能适应模型的气动特性变化,具有更强的鲁棒性。

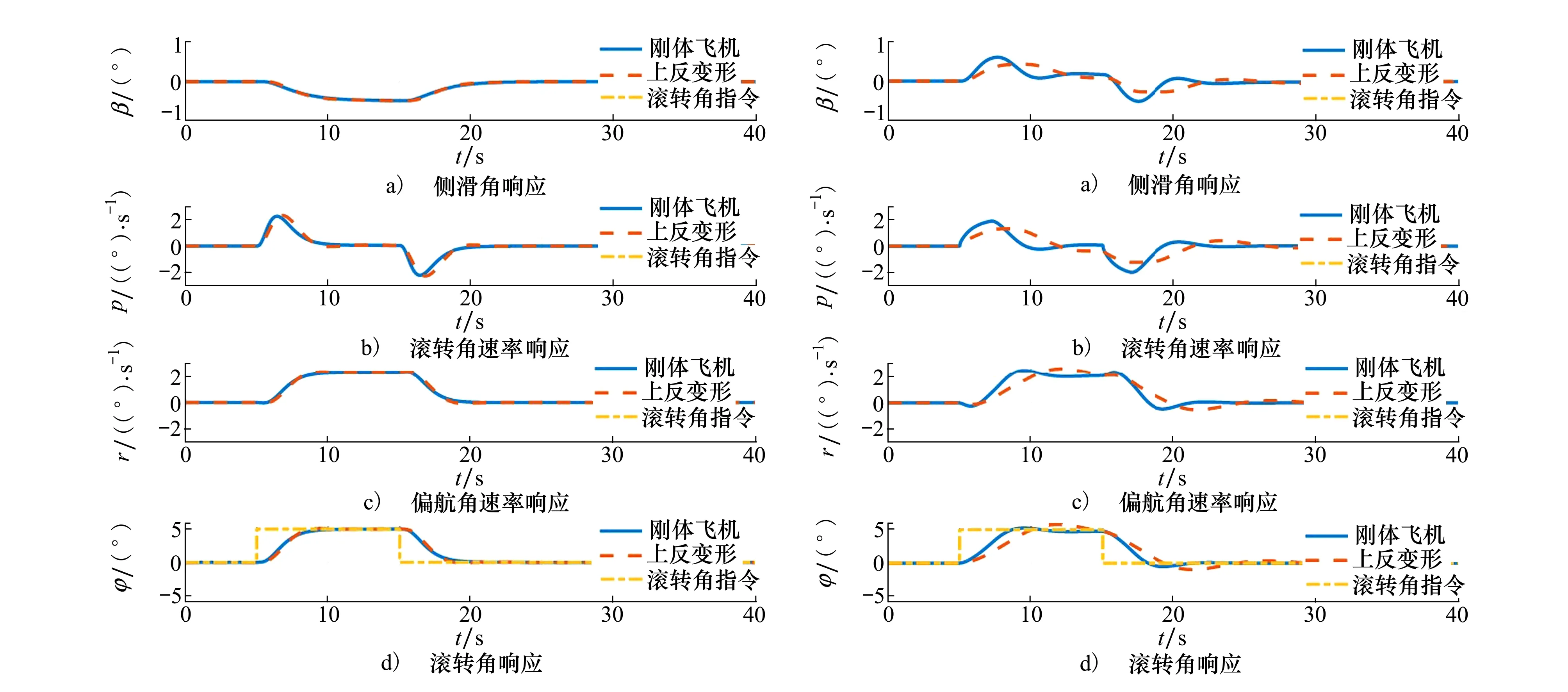
图11 自适应反步法控制响应 图12 PID控制响应

4.2 飞行试验验证

飞行试验中,飞机质量为218 kg,重心位置为35.5%平均气动弦长(MAC)。飞控系统采用自研成熟飞控计算机,包含核心板与扩展底板两大部分。组合导航采用MEMS组合惯导。大气数据系统选用AH型号空速管,用于测量空速、动压和静压。

根据太阳能无人机的飞行性能和姿态限制特性,设计的试验飞行航路如图13所示。飞机起飞离地后,初始爬升到100 m,改平后水平转过90°转换到下一段航路。在直线段爬升到巡航高度500 m，此时目标速度为16 m/s。着陆时,飞机首先在直线段从巡航高度500 m降低到进场高度100 m,并逐渐降速到15 m/s。水平转弯后进入进场航路点,然后保持0.5 m/s的下滑率稳定下滑。当判断飞机对准跑道且离地高度小于5 m时,目标下滑率改为0.2 m/s直至接地。为保证飞行过程中姿态不超限制包线,限制最大滚转角指令不超过5°,对应的航路转弯半径大于200 m。

图14～15是整个巡航阶段,俯仰姿态和滚转姿态的跟踪响应曲线。对姿态指令的跟踪控制精度在0.1°～0.2°的范围内。图16截取了飞行过程中1 600时刻到2 800时刻,约1 200 s的飞行试验数据。在这个时间段内,飞机存在较大的俯仰机动,俯仰角在-1°～4°的范围内变化,机翼上反角会随之发生变化,影响气动特性。但是,滚转角始终保持对指令良好的跟踪效果,未发生偏离现象。因此,飞行试验验证了自适应反步法能够实现较好的滚转姿态控制。

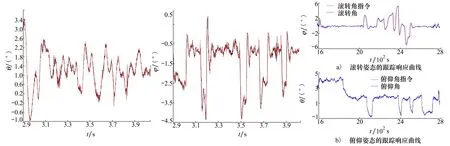
图14 俯仰姿态飞行试验数据 图15 滚转姿态飞行试验数据 图16 俯仰机动时的滚转姿态控制

5 结 论

针对大展弦比太阳能无人机的横航向稳定控制问题,本文具体对比分析了横航向气动特性和机翼变形的影响。通过根轨迹分析,揭示了飞机模态特性随机翼变形的变化规律。建立水平转弯平衡方程,计算了飞机的安全姿态限制边界。

针对太阳能无人机的气动特性、特征根受上反变形影响较大以及姿态限制等问题,本文提出了利用自适应反步法实现滚转角姿态的精确控制。基于此方法设计的控制律架构,不仅具有较好的速率和姿态控制精度,还具有较强的鲁棒性,在横向静稳定系数增大2.7倍,惯性矩Ixx增大约1.4倍的情况下,依然可以实现良好的跟踪控制。