一种基于最优集成随机森林的小样本数据特征提取方法

张维,张浩晨

(西北工业大学 机电学院,陕西 西安 710072)

在特征选择算法的研究中,随机森林(random forest,RF)算法[1]在构建决策树的过程中基于不纯度降低方法(mean decrease impurity)给特征进行排序。基于随机森林的RVS特征选择算法[2]，利用给特征加入噪声后的袋外数据(out of bag data)预测准确率与原始袋外数据预测准确率之差，描述特征重要性度量值，因其能够有效去除冗余信息、处理时间短且效率高，成为特征选择的主流方法[3]。以上2种传统的随机森林特征选择法在处理数据量充足且分布均衡的数据时特征提取效果良好，但是在处理小样本数据时由于训练样本少，构建决策树分类时极易出现过拟合[4]，导致计算特征重要性度量值时不稳定且精度低，降低了特征提取的有效性。

采用随机森林对高维小样本数据进行特征提取的难点主要在于样本量缺乏以及决策树的稳定性差、精度低。徐少成等[5]提出了基于随机森林的加权特征选择算法，采用单棵决策树的权重与特征重要性度量值加权平均得到最终的特征重要性度量值，提升了随机森林特征提取的精度，但是该方法在处理小样本数据时不能有效提升决策树集合的稳定性[6]。Khan等[7]总结了最优树集合思想(optimal tree ensemble)，认为随机森林中单株树的预测精度对最终分类有极大影响，提出了一种基于个体准确性和多样性的决策树选择方法，提升了随机森林分类的精度以及稳定性，该方法应用于小样本数据特征提取中可大大提升决策树集合的稳定性，但是该方法并未考虑小样本所带来的过拟合和特征提取精度低问题[8]。本文结合小样本数据在特征提取过程中出现的难点，提出了OTE-GWRFFS算法，结合生成式对抗网络(GAN)生成相似数据[9]，并采用改进的非局部均值去噪算法[10]修正生成数据的分布误差，利用基于权重的最优树算法计算特征的重要性度量值，提高了小样本数据特征提取的精度、稳定性以及有效性。

1 OTE-GWRFFS算法

随机森林在对高维小样本数据进行分类过程中，存在因样本量的缺乏导致训练深度不够以及过拟合现象。而利用袋外数据进行特征重要性度量值计算时，又有可信度低以及特征排序稳定性差问题。针对小样本数据在特征提取过程出现的问题，本文提出了一种基于最优集成随机森林的小样本数据特征提取方法(OTE-GWRFFS算法)。OTE-GWRFFS算法的流程如图1所示。

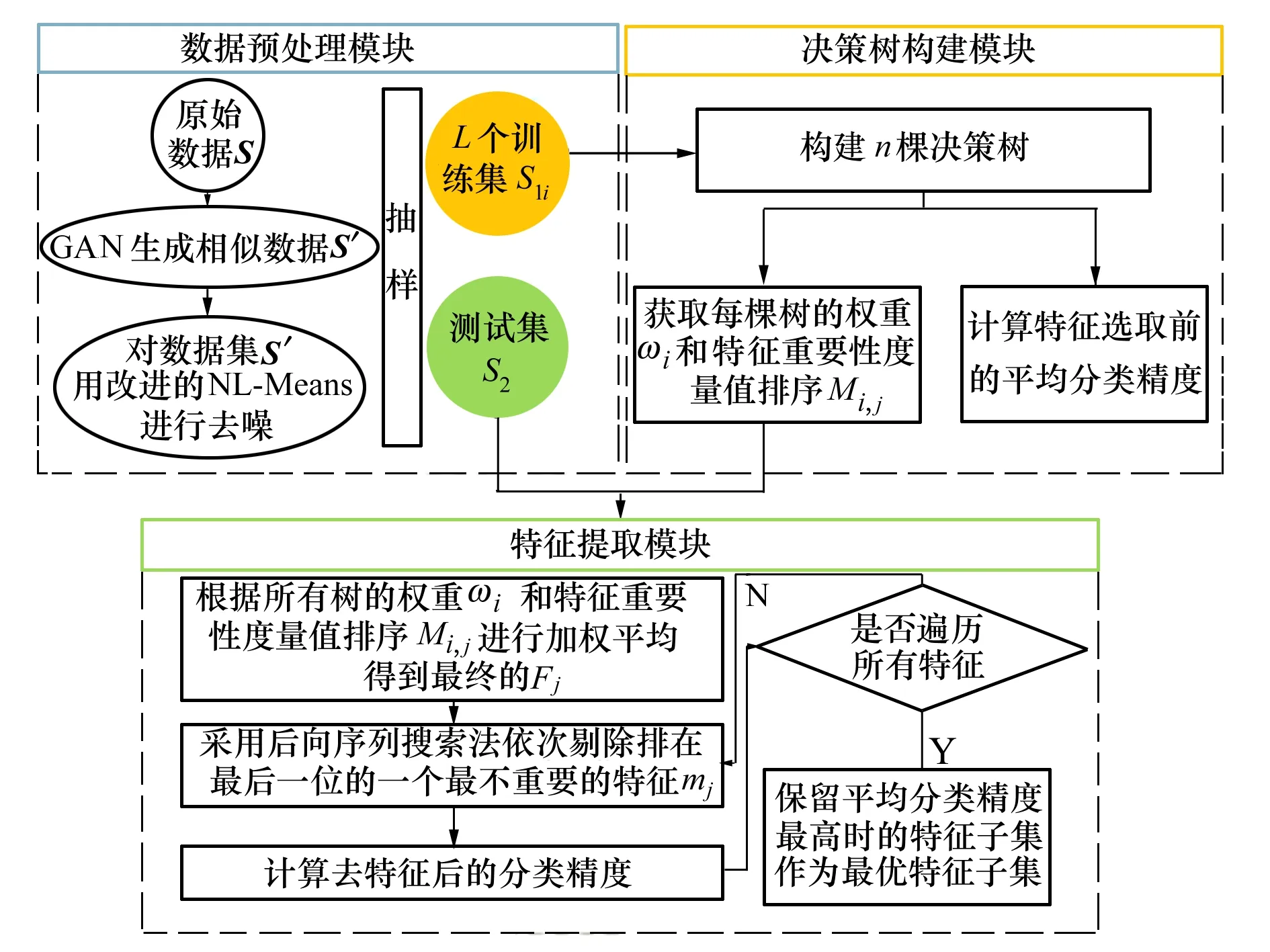
图1 OTE-GWRFFS算法流程图

1.1 OTE-GWRFFS算法流程

OTE-GWRFFS算法的具体步骤如下所示。

输入：原始数据集S：包括样本数N和样本特征A=(A1,A2,A3,…,AM)

构建的随机森林的决策树个数n

输出：样本特征Aj的最终特征重要性度量值Fj

算法：

step1 初始化原始数据集S，设置构建随机森林的决策树个数n

step2 利用GAN算法对原始数据集进行数据增强，得到生成数据集S′

step3 利用改进的NL-Means对生成数据集S′进行个别离群点的拟合得到数据集S″

step4 采用bagging抽样，构成L个训练数据集S1i(i=1,2,…,L)，一个测试数据集S2，每个训练数据集中有N′个样本数据，m个样本特征

step5 对数据集S1i进行决策树的构建

step6 for (i=1 ton)

计算所有决策树的精度Ai

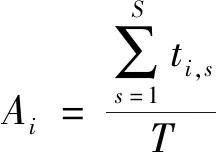
(1)

式中：Ai为第i棵决策树的分类精度；T为测试集样本数量；ti,s为第i棵决策树对测试样本的分类与样本真实分类相同的样本数目

将所有树的Ai按照由大到小排序

for(i=1 Ton)

逐次去除后n′棵树并计算最终的分类精度A

if (A减小)

break

step7 for(i=1 ton-n′)

计算决策树的权重ωi

(2)

式中：ωi代表第i棵树的权重；ti,e代表第i棵决策树对测试样本的分类与随机森林所有树对测试样本的分类相同的样本数目；T代表测试集的样本数量。

计算第i棵决策树中第j特征的重要性度量值Mi,j

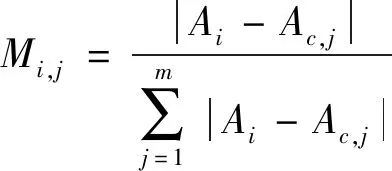
(3)

式中，Ac,j定义为给测试集中第j个特征加入高斯噪声后的平均分类精度。

step8 最终的特征重要性度量值Fj

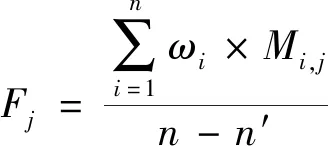
(4)

在计算完特征重要性度量值后，需要摒弃重要程度不高的特征，即采用后向搜索法，逐一去除重要程度靠后的特征并计算去除该特征后的平均分类精度，保留剩余最优特征子集的评判标准即去除该特征及排名低于该特征的其他特征后的平均分类精度达到最高。

1.2 时间复杂度分析

本文所提出的OTE-GWRFFS算法中基分类器选择CART算法。假设本算法中训练数据集的特征维数为M，训练样本个数为N，随机森林在构建CART树的过程中，从N个训练样本中利用bagging抽取N′个训练样本，从M个特征中随机选择m个特征计算信息增益，并且对树的生长不进行剪枝。在本实验中，采用序列后向选择策略进行最优树的选择需要循环(n-p)次，特征选择需要循环(m-p)次(p由数据集特征数决定，一般不少于5个)，根据排序后的特征集合生成新的训练数据集需要进行(m-p)次计算，每次计算时间为常数，故本算法总的时间复杂度可以近似表示为

由(5)式可见，OTE-GWRFFS算法的时间复杂度与特征维数m呈近似平方关系，与训练数据集样本个数N′呈近似立方关系，对于高维小样本数据，运算时间是可以接受的，算法具有较好的扩展性。

2 小样本数据扩充

数据量小在特征选择过程中是影响特征排序精度以及稳定性的主要原因，从算法层面改进超参数设定的方法始终存在局限性[11]，从数据层面通过数据增强技术扩充数据解决数据量小的问题，是提高特征选择精度以及稳定性的一种有效方法。本文依据表格数据与图像之间的等价性利用GAN对小样本数据集进行数据扩充。由于生成的数据在反归一化过程中会因小程度的偏差最终反映出较大的偏离，本文采用基于表格数据的非局部均值算法(NLM)对生成数据进行修正，提高生成数据与原始数据之间的分布相似性。数据生成模型如图2所示。

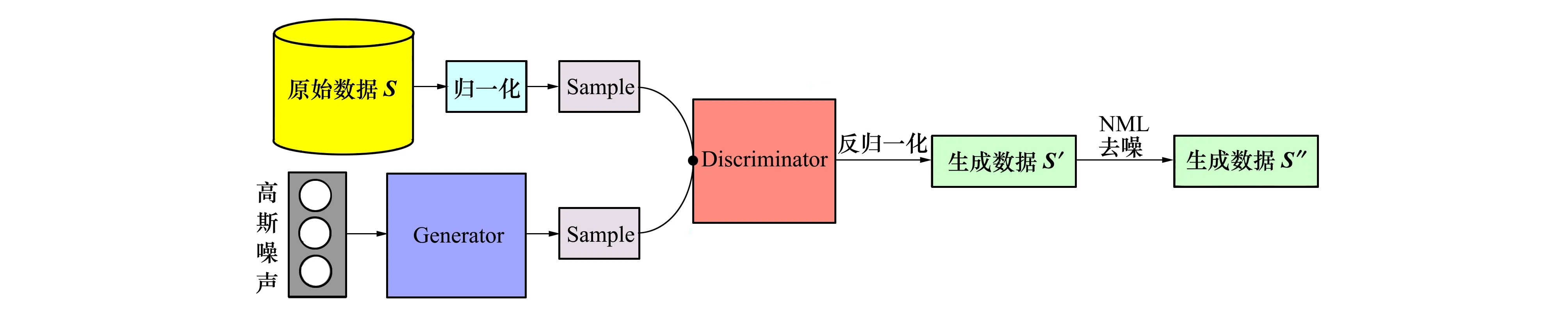
图2 数据生成模型图

1) 数据生成

任意高斯噪声序列通过生成器将原低维向量投影成为与原始数据维度一致的高维向量，通过判别器将归一化后的原始数据S与生成的高维向量进行分布相似性判断，经过不断训练生成器和判别器，最终可以生成分布相似的数据，再经反归一化得到生成数据S′。

2) 数据分布修正

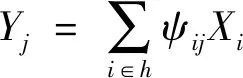
(6)

式中

该数据生成模型通过提升生成数据S′和原始数据S的数据分布相似性解决了表格数据生成的偏离问题，同时数据量的扩增也避免了过拟合现象，提升了特征排序精度以及稳定性。

3 基于权重的最优树集合

在生成对抗网络的小样本数据扩充后，扩充样本与原始数据集有着一定的偏离性，不能真实地还原原始数据集的特征分布，因此在训练随机森林的过程中，某些决策树在随机分配训练数据集时被分到过多的生成数据，导致在测试数据集中分类效果极差[12]，影响了特征重要性度量值的准确度，为了避免该问题的出现，本文采用集合高精度以及高多样性基分类器的方法，将训练好的基分类器按照分类精度排序并选取精度高的分类器作为最优决策树集合，可以在不影响决策树多样性的前提下降低不同类型模型的归纳偏差。

1) 分类错误率

为了挑选出分类性能最优的树，每棵树对测试集的分类错误率(分类精度)按(1)式计算。

根据所计算出每棵树的分类错误率(分类精度)将所有树的Ai按照由大到小排序，按照后向搜索法逐次选取前n′棵树并计算最终的平均分类精度A，选取终止条件为最终平均分类精度A呈现下降趋势且基分类器数量有集成决策意义即可。

2) 特征重要性度量

在得到最优树集合后，对决策树给予不同权重再次综合评估特征重要性度量值。原始数据集S通过bagging抽样后会获得L个训练样本集S1i(i=1,2,…,L)和一个样本数为T的测试集S2，这n个训练样本集可以产生n棵决策树，根据决策树的预测结果可以获得一个T×(n+2)的矩阵，如表1所示。

表1 n=7，T=5的决策矩阵

表1中第i棵决策树的可信度(权重)可由(9)式得到

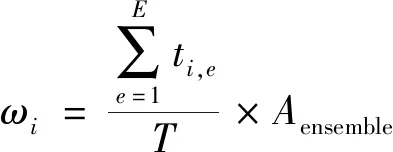
(9)

式中：ti,e代表第i棵树中对T个测试样本的分类结果和决策结果中一致的数量，Aensemble表示集成预测的准确率，即决策结果与原始分类的相符程度。由于每棵决策树的Aensemble值都是一样的，是否考虑Aensemble的作用对排序结果没有影响，在计算权重时加入这个因素，其目的是尽量缩小各决策树间权重的相对差距。

4 实验验证

为验证本OTE-GWRFFS算法在高维小样本数据集上的有效性，在UCI数据集中挑选了5个具有代表性的小样本数据集。对于每个数据集，都首先利用GAN进行样本扩充，样本扩充的原则即保证原始数据集的分布特征，样本扩充量不能超过原始数据集的样本数，保证了在bagging抽样时训练集有足够充分的原始样本。表2列出了这些数据集名称、特征以及数据扩充结果。

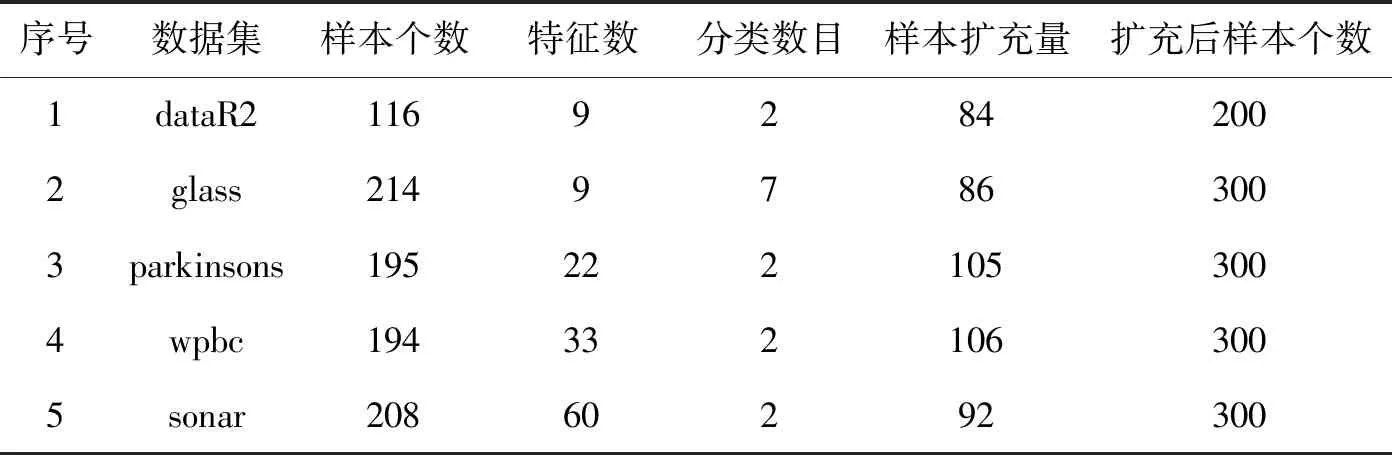
表2 UCI中小样本实验数据汇总

为了验证最优树集合算法(OTE)的有效性，图3展示了5个数据集在后向搜索法过程中摒弃分类精度低的决策树后对测试集的分类精度。可以看出每个数据集在选择最优树过程中都有一个精度峰值，此峰值所对应的决策树量即最优树数量，表明最优树集合算法(OTE)可以有效选择出分类精度最高的树。

图3 最优树集分类精度图

表3列出了所用数据集在利用RFFS、WRFFS以及OTE-GWRFFS算法进行特征选择后得到的特征子集个数，选择依据为各算法对特征重要性度量值进行排序并采用后向搜索法选择后分类精度达到最高时的特征子集个数。经过特征子集个数的筛选，RFFS、WRFFS以及OTE-GWRFFS算法的维数平均下降率分别为25.68%,25.04%和34.20%。

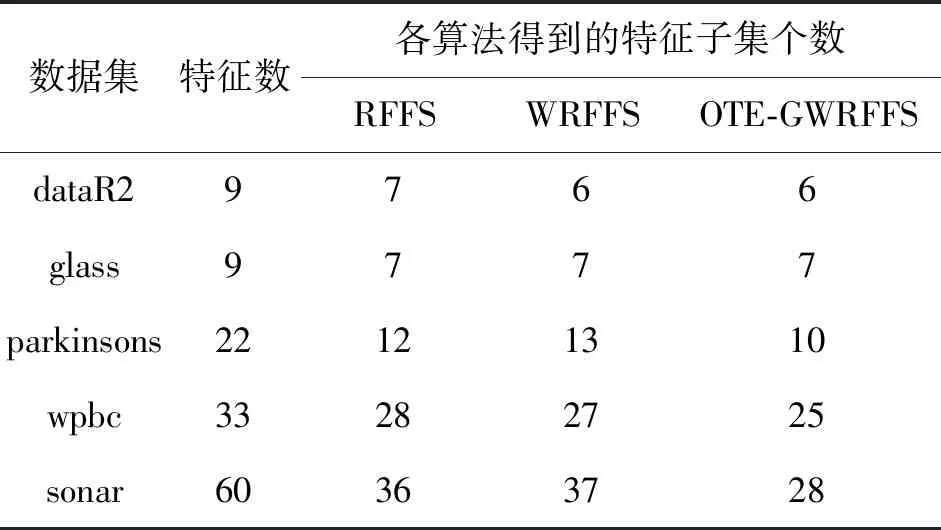
表3 各算法特征选择结果

表4给出了所有数据集在进行特征选择前的分类精度，以及利用RFFS、WRFFS和OTE-GWRFFS算法进行特征选择后，再次对特征选择后的数据集进行分类，经过对比，RFFS、WRFFS以及OTE-GWRFFS算法的分类精度平均提升率分别为7.91%,9.42%和13.39%。

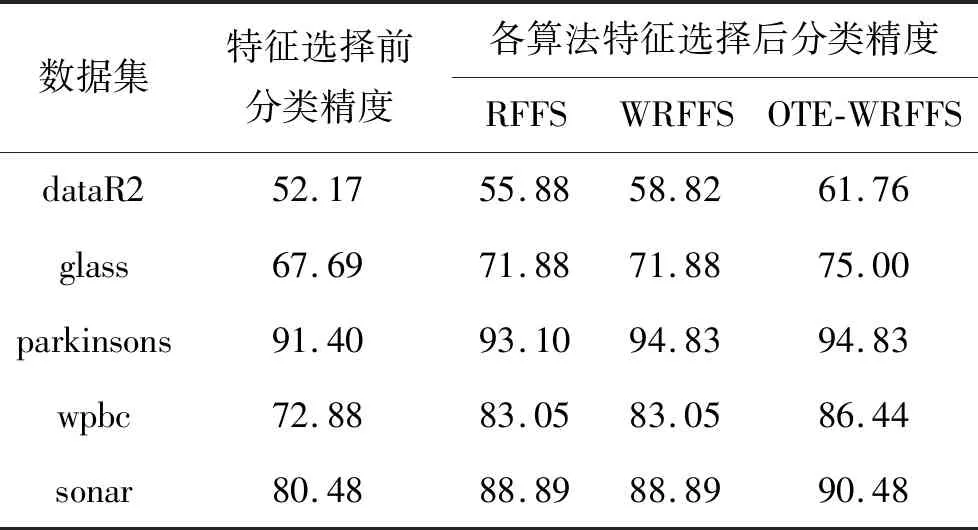
表4 各算法特征选择前后分类精度对比 %

表5给出了所有数据集在未进行特征提取前以及经过各算法特征提取后的F1-score值。

为了清楚表达本算法在特征提取方面优于RFFS、WRFFS算法，图4展示了3种算法在特征提取过程中随着特征数的降低，其分类精度的变化曲线。

表5 各算法特征选择前后的F1-score值

图4 降维精度对比图

表6给出了数据扩充算法前后的最优特征子集数和分类精度对比，经数据扩充后算法的维数平均筛除提升率为9.16%,分类精度平均提升率为6.96%，验证最优树集合算法对小样本数据扩充的有效性。

表6 数据扩充前后OTE算法的特征选择精度对比

根据对表3的特征选择结果和表4的特征选择前后分类精度对比以及表5计算的分类F1-score值可知，本算法在基于相同的数据集进行特征选择后维数的平均下降率为34.20%，而RFFS以及WRFFS算法的维数平均下降率大约仅有25%，且经过本算法特征降维后再次分类的F1-score值达到最高。可以证明本文算法相比于RFFS以及WRFFS算法有较大提升。表4展示了删除冗余特征后本算法再次进行分类，分类精度提升率达到13.39%，而RFFS以及WRFFS算法的分类精度提升率大约仅有8%，同时在特征提取后进行再次分类的F1-score值有明显提升，说明本算法能够最大程度地对特征进行降维处理，能够更有效地删除冗余特征，并且特征选择精度更高。表6用数据扩充前后的分类精度作为对比，可以看出在用于验证的数据集中，数据扩充对维数平均筛除提升率约为9.16%，分类精度的提升率大约在6.96%，可以证明数据扩充在处理小样本数据时有效地提升了特征选择的精度以及稳定性。

结合实验结果，在特征选择的维数平均下降率以及在分类精度方面，本算法都比其他2种算法更有效、精度更高。由于选取的数据具有广泛的代表性，所以说本算法在特征选择上具有更强的适用性。且本算法在针对于极小样本数据集时也具有有效性，可以完全避免过拟合现象且特征提取效果良好。

5 结 论

高维小样本数据的特征降维极容易出现特征排序不稳定，经常会将关键特征作为不重要特征处理，大大影响了降维的精度，不利于后续数据挖掘工作。本文基于小样本的降维问题，提出了基于最优集成随机森林的小样本数据特征提取方法OTE-GWRFFS。建立数据增强模型，在数据扩充的基础上，采用改进的NL-Means去噪法以及最优树集合OTE思想改善数据扩增过程中出现的数据偏差性质，通过给予最优树集合以不同权重再次提升每棵决策树的重要性度量的可靠性。实验表明OTE-GWRFFS算法可以避免随机森林过拟合问题，提升了特征排序的稳定性及精度，在经过特征选择后，随机森林分类精度明显提升。