百页轮柔性抛光力与法向位移关系模型研究

张军锋,史耀耀,蔺小军,吴晓君

(1.西安建筑科技大学 机电工程学院,陕西 西安 710055;2.西北工业大学 航空发动机高性能制造工业和信息化部重点实验室,陕西 西安 710072)

目前国内复杂薄壁曲面构件(如航空发动机整体叶盘)的精密成形加工，大多采用球头铣刀与多坐标数控点切触、行切铣削工艺，表面完整性无法满足设计要求。实验研究表明，五轴数控+弹性磨具(如百页轮)的柔性抛光工艺是提高复杂薄壁曲面构件表面质量的有效方法之一。尽管弹性磨具的弹性变形可使磨具和复杂曲面实现良好接触，有效减小抛光力变化及加工振动对抛光表面质量的影响，但也导致抛光力处于动态变化状态。抛光加工的特点之一是只设定抛光力而不设定与磨削深度相对应的磨削用量参数[1]，其值通过磨具与工件的法向位移来调控。因此，建立百页轮柔性抛光力与法向位移的关系模型对抛光力、材料去除率和表面完整性的控制具有重要意义。

目前，关于柔性抛光力的建模学者们开展了一定研究，而针对抛光力及法向位移(磨具-工件法向变形量)的研究较少。Tang等[2]将磨削力分解为切屑力与划擦力，依据剪切应力、应力变化率以及磨削热对切屑的影响建立了切屑力模型，基于磨削参数对摩擦因数影响规律分析建立了划擦力模型，最终得到了磨削力数学模型。Feng等[3]基于Archard摩擦学方程和具体工艺参数导出接触区域内平面和曲面抛光的压力分布模型，并通过抛光实验进行验证。Xian等[4]假定磨具与工件的接触应力符合三角函数和二次分布，利用曲面积分方法建立了2种抛光力模型，并通过抛光实验进行验证。史永杰[5]基于固体表面的接触理论及模型，在假设研抛头表面磨粒高度服从高斯分布的基础上，建立了法向位移与研抛力关系的理论模型，进而得到了力-位-姿耦合模型。黄智等[6]利用有限元方法得出砂带与工件之间的压痕及实际接触面积，结合单位面积砂带磨粒磨削TC4数值模型仿真出磨削力，根据相关数据算出待定参数，最后结合有效磨削面积预测砂带磨削力。淮文博等[7]通过正交试验和极差法确定了影响抛光力的主要参数并利用正交试验得出了砂布轮柔性抛光力的经验预测模型。

上述研究为复杂曲面柔性抛光的实际应用提供了参考，本文在其基础上，基于弹塑性接触理论进行单颗磨粒作用时抛光力及工件变形量研究，然后结合百页轮表面磨粒分布函数建立了抛光力与法向位移关系模型，最后通过数值仿真和抛光实验对所建立关系模型的正确性进行验证。

1 百页轮表面磨粒分布函数

百页轮是将砂带页片粘结固定在塑料芯轴上形成的一种涂附磨具，其磨料、磨粒大小和直径尺寸选择自由度大，且外形还可根据需要进行修整。百页轮抛光具有柔性和可达性好、表面质量高和冷态抛光等特点，非常适合抛光发动机整体叶盘等开敞性差的复杂曲面构件(见图1)。由于百页轮表面磨粒分布高低不齐(见图2)，为了方便研究，考虑到静电植砂特点及砂带页片的结构特性[8]，本文将百页轮等效成如图1所示的3层结构：中间层为具有良好弹性的基体，基体表面为单层磨料且分布均匀，基体内侧是刚性较好的塑料芯轴。

据此可得百页轮表面磨粒的凸出高度近似符合正态分布[9-10](见图3)，其分布函数如(1)式所示。从(1)式可知，磨粒凸出高度的分布规律与磨粒的平均大小及分布有关。

图1 百页轮结构及应用 图2 百页轮表面磨粒分布图3 百页轮表面磨粒凸出示意图

(1)

式中:z为磨粒凸出高度;σ为凸出高度标准差。

由图3可知,接触区同时切削的磨粒数量与工件表面和参考平面的距离z0有关。只有z>z0时,磨粒与工件表面才开始接触,即二者之间的切入深度或变形量为δmw=z-z0。假定每个磨粒都垂直于基体、尖端向外且只有一个有效磨刃,则有效磨刃数就等于表面磨粒。同时假定磨粒间的平均间距等于磨粒平均直径dm。由此可得百页轮表面单位面积内参与接触的磨粒数(静态有效磨刃数)Ns为

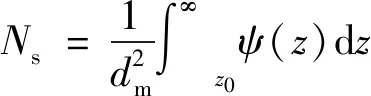
(2)

式中，dm为磨粒大小均值。

进而可得单位时间内经过接触区的动态有效磨刃数Nd为[11]

(3)

式中:Vs为线速度；n为主轴转速;D为百页轮直径;b为百页轮和工件的接触宽度,平面抛光时为百页轮宽度。

2 抛光力与法向位移关系模型

2.1 法向位移变化过程

在百页轮基体、磨粒和工件三者接触作用过程中,假设百页轮表面磨粒没有磨损或脱落,基体和工件通过磨粒进行抛光力的承担和传递。在抛光力作用下,开始时磨粒切入工件的深度很小,其表面仅产生弹性变形;当抛光力逐渐增大,工件表面开始产生塑性变形,随着抛光力持续增大,磨粒切入深度不断增加,最终实现工件材料的切除。由于力作用的相互性以及百页轮基体的良好弹性,忽略百页轮基体的塑性变形,仅考虑其弹性变形。

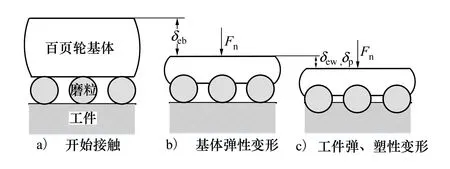
图4 抛光过程法向位移的变化

综上可知,法向位移包含两部分:百页轮基体的弹性变形量δeb,工件的弹、塑性变形量δew,δp。本文先进行单颗磨粒和工件的接触作用过程研究,然后进行抛光力和法向位移的关系模型研究。为方便分析,做如下假设:

1) 百页轮表面磨粒均为球形;

2) 由于磨粒硬度远大于工件硬度,故而忽略磨粒变形对法向位移的影响;

3) 不考虑磨粒的磨损或脱落、环境温度和湿度等变化的影响。

2.2 抛光力与法向位移关系模型建立

2.2.1 单颗磨粒作用时的抛光力与法向位移

磨粒和工件开始接触作用时,由于抛光力Fgne较小,工件仅产生弹性变形,如图5所示。根据Hertz弹性接触理论[12]可知,抛光力Fgne和弹性变形量δew的表达式如(4)式所示。

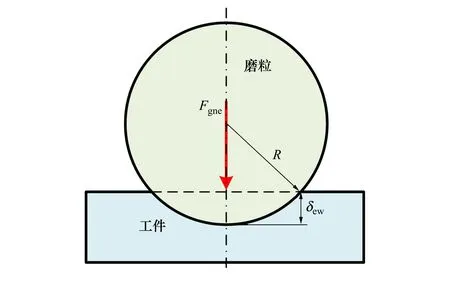
图5 单颗磨粒与工件的接触作用

(4)

式中:R为磨粒半径;Emw为磨粒与工件的等效弹性模量;Em,Ew分别为磨粒、工件材料的弹性模量;νm,νw分别为磨粒、工件材料的泊松比。

随着抛光力进一步增大,磨粒和工件之间的接触变形由弹性变形逐渐转变为塑性变形。相关研究表明,磨粒与工件之间弹-塑性变形的临界条件如(5)式所示[13]。

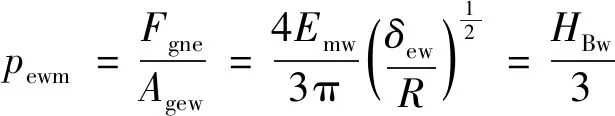
(5)

式中:pewm为磨粒和工件之间的平均抛光压力;HBw为工件材料的布氏硬度。

由此可得,磨粒与工件之间由弹性变形向塑性变形转变的临界变形量如(6)式所示。即当磨粒与工件之间的变形量δmw<δ0时,二者之间只产生弹性变形,此时磨粒-工件变形量和工件的弹性变形量大小相同,即δmw=δew。

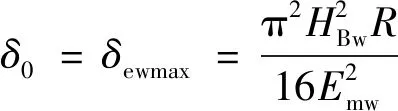
(6)

研究表明,磨粒与工件发生完全塑性变形的临界变形量为δc=110δ0[14]。当δmw≥δc时,磨粒与工件之间发生完全塑性变形,二者之间的平均抛光压力ppm为一个恒值,其大小等于工件材料的布氏硬度,即ppm=HBw。由此可得,完全塑性变形阶段抛光力Fgnp的计算公式如(7)式所示[15]。此时,磨粒-工件变形量δmw等于工件的塑性变形量δp,即δmw=δp。

Fgnp=AgpHBw=2πRHBwδp

(7)

式中，δp为塑性变形量。

当δ0≤δmw<δc时,工件弹性变形和塑性变形并存,磨粒与工件间的接触面积Aep和平均抛光压力pepm分别如(8)和(9)式所示[16]。

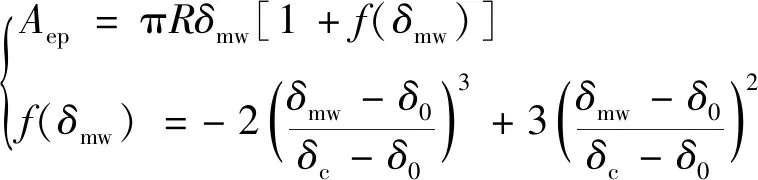
(8)

(9)

式中,kmp为平均抛光压力系数,本文取kmp=1/3。

由此可得,弹塑性变形阶段抛光力Fgnep的表达式如(10)式所示。此时,磨粒-工件变形量为弹、塑性变形量之和,即δmw=δew+δp。

Fgnep=Aeppepm=πRHBwKδδmw[1+f(δmw)]

(10)

2.2.2 抛光力与法向位移关系模型

由于百页轮表面磨粒的凸出高度差异,不同磨粒抛光作用不同。凸出磨粒完成工件表面材料的切削,作用过程历经弹性、弹塑性和完全塑性变形3个阶段并产生切屑。凸出高度较低或较钝的磨粒耕犁工件,作用过程历经弹性和弹塑性变形2个阶段或上述3个阶段(无切屑产生)。而磨钝或相对凹下的磨粒只是与工件表面产生滑擦,仅产生弹性变形。考虑到接触区所有参与接触的磨粒对抛光力均有贡献,抛光力的计算公式为

(4)提高产品的可设计性。CFRP性能多样，其物理性能、化学性能、力学性能均可以通过合理选择原材料的种类、配比、加工方法、纤维含量和铺层方式进行设计。由于树脂基体材料种类很多，其选材设计的自由度很大，这是传统的各向同性材料(比如钢、铝)所不具备的。另外，CFRP可以实现一体化制造，其制品是由材料和结构同时完成，即通过合理的模具设计，把不同厚度的零件、凸起部分、筋和棱等全部一体成型。整体成型同时还能提高结构的完整性、气密性和保温性，以及提高车辆舒适度。

Fn=∑(Fgne+Fgnep+Fgnp)

(11)

将(3)、(4)、(7)和(10)式代入(11)式可得接触区总的抛光力，如(12)式所示。由(12)式可知,抛光力大小和同时参与切削的磨粒数量、磨粒切入工件深度(z-z0)、主轴转速、磨粒大小等有关。

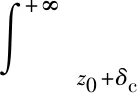
(12)

考虑到百页轮表面磨粒的受力平衡,根据Hertz接触理论可得百页轮的弹性变形量δeb为

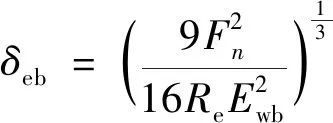
(13)

综上可知,磨具和工件之间总法向位移δt为

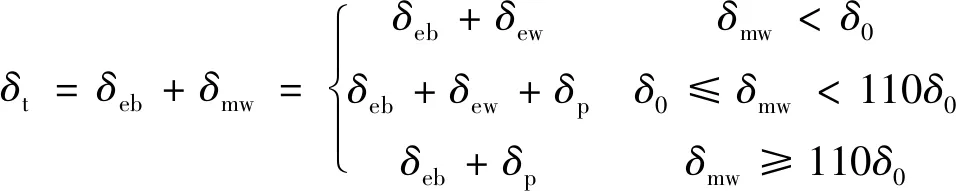
(14)

2.3 抛光力与法向位移关系模型仿真分析

以采用粒度240#(dm为56.5 μm)的棕刚玉磨粒的百页轮(直径16 mm,宽度12 mm)进行TC4平板试件抛光为例进行抛光力与法向位移的仿真分析,主轴转速为7 500 r/min,其余仿真参数如表1所示。

表1 相关仿真参数[17]

从图6可知,无论是单颗磨粒单独作用,还是接触区所有磨粒共同作用,抛光力均随磨粒半径的增大而增大(也即随粒度S的减小而增大),并且塑性变形阶段抛光力远大于弹塑性阶段和弹性变形阶段的抛光力。另外,图6b)中当R在28～58 μm范围内时,Fn的变化曲线有一个凸峰,造成这一结果的原因是:当R=32 μm(S=220#),38.25 μm(S=180#),45 μm(S=150#)时,磨粒大小标准差σ快速增大并在R=58 μm(S=120#)时回归正常。由此可见,σ对抛光力Fn的变化有直接影响,由于σ越大说明磨粒的等高性越差,可见磨粒等高性越好,抛光力变化也越平稳。

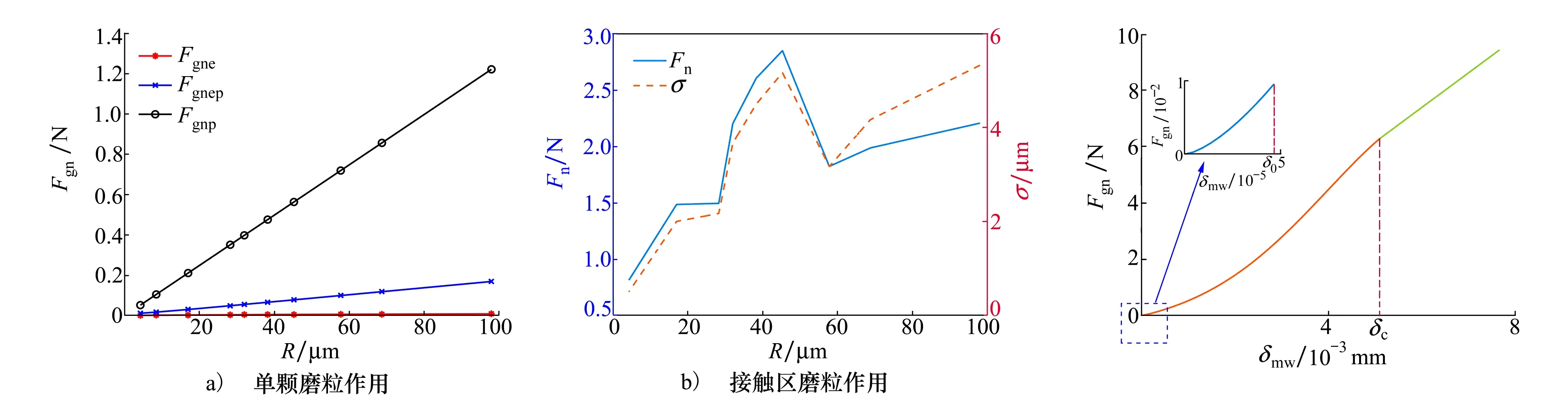
图6 磨粒半径R对抛光力的影响图7 抛光力随法向位移的变化

从图7可知,磨粒与工件的接触作用过程中,抛光力Fgn随着磨粒-工件变形量δmw的增大而增大。其中,在塑性变形阶段(δmw>δc),二者之间为线性关系,并且在整个接触作用过程,弹性变形量远小于塑性变形量,即δewmax=δ0≪δp,由此可得δmw≈δp,同时结合(7)式，(14)式可简化为(15)式,也即百页轮和工件间的总法向位移可以用百页轮的弹性变形量和工件的塑性变形量之和来代替。

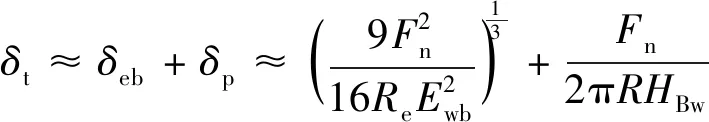
(15)

从图8可知,当抛光力从小到大变化时,总法向位移和磨具变形量也从小增大,并且增大趋势逐渐趋缓,变化曲线近似为抛物线,同时工件塑性变形量远小于磨具的弹性变形量和总法向位移,而法向位移与工件弹性变形量大小十分接近。故而,(15)式可进一步简化为(16)式,即可用百页轮的弹性变形量来代替百页轮和工件的总法向位移,这也为实际抛光过程中通过调节百页轮变形量来进行抛光力控制提供了有效的依据和支撑。

(16)

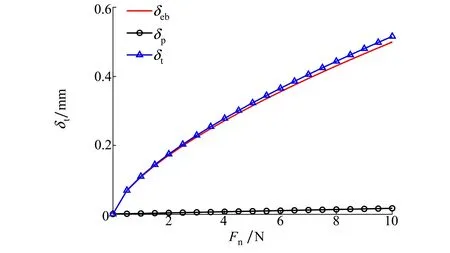
图8 法向位移随抛光力的变化

(17)

图9 抛光力随法向位移的变化

3 模型验证

3.1 百页轮弹性变形量范围

通过抛光实验发现，当百页轮变形量较大也即抛光力较大时，容易引起加工颤振。因此，有必要确定百页轮变形量δ的最大范围。百页轮变形量范围研究实验在作者所在团队研制的五轴联动数控抛光机床上进行，如图10所示。

图10 百页轮变形量范围确定实验

TC4平板试件下装有压力传感器并和显示仪相连，用来读取抛光力数值。抛光时将主轴旋转到水平方向(与试件表面平行)，然后沿Z轴方向移动主轴来调整法向位移。假设百页轮和工件刚接触时法向位移为Z0(百页轮变形量为0)，调节后的Z轴坐标为Z1，则ΔZ=Z1-Z0即为百页轮的变形量。由于机床Z轴平均运动误差为3.852 μm，故可以保证法向位移精度。百页轮粒度为240#，直径16 mm，实验主轴转速分别为4 500,6 000和7 500 r/min，磨粒材质为棕刚玉，变形量范围为0～2 mm。实验过程中，分别测量不同百页轮变形量情况下抛光力的最大值和最小值，将抛光力的最大-最小值之差ΔFn作为抛光力的跳动量，实验结果如图11所示。

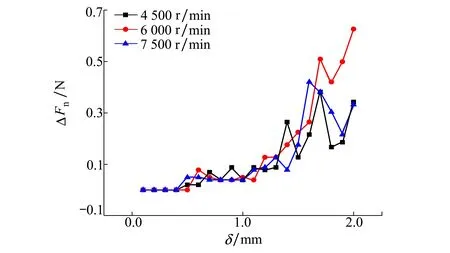
图11 不同转速时抛光力的波动

从图11可知，当百页轮变形量δ≤0.5 mm时，抛光力最大-最小值之差几乎为零，抛光力相对比较稳定；当0.5<δ≤1.3 mm时，抛光力存在少量波动；而当δ>1.3 mm时，主轴颤振较大，抛光力波动量比较大。因此，当百页轮初始直径为16 mm时，百页轮的变形范围为δ≤1.3 mm。

3.2 抛光力与法向位移模型验证

为了验证磨粒粒度(半径)和法向位移对抛光力的影响，选用3种不同的百页轮粒度，分别为：120#(R=57.75 μm)，240#(R=28.25 μm)，400#(R=8.5 μm)。

为了提高验证结果的可靠性，选用3种不同的主轴转速，具体为4 500,6 000和7 500 r/min。

当百页轮与工件刚接触时，抛光力与法向位移均为0，百页轮变形量同样通过Z向移动主轴来调节，增量为0.1 mm，百页轮变形量范围为δ≤1.3 mm。记录不同粒度和法向位移所对应的抛光力，将抛光力最大值和最小值的平均值作为抛光力的检测结果。实验验证结果如图12～13所示。

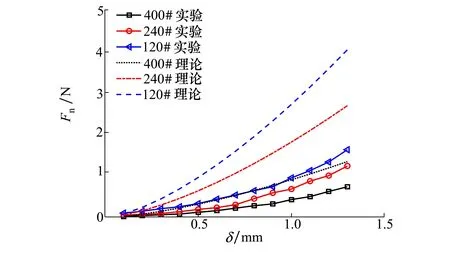
图12 实验结果和理论结果对比

图13 粒度和接触位移对抛光力的影响(n=7 500 r/min)

从图12可知，不同主轴转速时，抛光力均随百页轮变形量的增大而增大，且实验曲线和理论曲线变化趋势一致。图12中实验结果小于理论结果，原因在于模型推导过程中存在一定的假设和近似。另外，图12中n=4 500和6 000 r/min的曲线存在一定交叉，可能的原因是测量误差，但并不影响相关结论的获得。

从图13可知，抛光力随百页轮粒度的减小而增大，由于磨粒粒度和磨粒直径一一对应且呈反比,即抛光力随着磨粒半径增大而增大,和2.3节仿真结果相一致。从图13还可知，抛光力随法向位移(百页轮变形量)的增大而增大，并且增大趋势逐渐增快，同时变化曲线近似为二次分布(图中虚线)，亦与2.3节仿真结果相符合。从而证明本文所建抛光力和法向位移关系模型的正确性。

另外，实验结果在磨粒半径从28到58 μm变化时，抛光力没有出现突变，和仿真结果不一致。原因在于：磨粒标准差一定程度上反映的是磨具表面磨粒分布的等高性，而百页轮的结构特性提高了磨粒的等高性，具体体现在2个方面：①百页轮的砂带页片上的磨粒通常采用静电植砂方式，其表面磨粒分布均匀且锋刃性好；②百页轮基体柔性良好，抛光时少量突出的磨刃被压向砂带页片的粘接剂和基材，进一步提高了同时参与切削作用磨刃的等高性，这也体现了百页轮抛光的优越性。

4 结 论

1) 基于弹塑性接触理论分析单颗磨粒作用时抛光力与工件变形量，结合百页轮表面磨粒分布函数建立了抛光力和法向位移的关系模型，并通过数值仿真和实验验证了所建模型的正确性。

2) 百页轮柔性抛光过程中的法向位移主要表现为百页轮的弹性变形，抛光力随着法向位移的增大而增大，且二者之间变化近似符合抛物线分布；磨粒粒度是影响抛光力的重要参数，抛光力随着磨粒粒度的增大而减小。

3) 本文所建抛光力和法向位移的关系模型不仅为百页轮柔性抛光力及表面完整性控制提供了理论支持，而且可为其他光整加工表面完整性的控制提供方法借鉴。