基于凸多面体碰撞检测的虚拟砂轮建模研究

2022-01-27徐秀玲于天彪

中国机械工程 2022年2期

陈豪赵继徐秀玲于天彪

东北大学机械工程与自动化学院，沈阳，110819

0 引言

磨削是精密制造的关键技术之一，被广泛应用于精密零件的加工制造。虽然磨削加工具有较长的历史，但由于磨削过程比较复杂，磨削机理至今仍然是精密加工的研究热点之一[1]。在计算机技术高速发展的今天，仿真技术通常被应用于磨削机理的研究以及加工参数的优化，其中，虚拟砂轮建模是磨削过程仿真的基础。虚拟砂轮建模的研究，有利于磨削表面质量的预测，对磨削技术的改进提高具有重要的意义。

目前，虚拟砂轮建模的方法主要有三类。第一类是利用检测设备对实际砂轮表面进行检测，根据砂轮表面的三维数据进行重构。XIE等[2]对砂轮表面形貌进行测量并提出砂轮表面评价方法，线性拟合砂轮表面形貌，并对其进行了量化。第二类是利用高斯随机粗糙表面去模拟实际的砂轮表面，认为模拟的随机粗糙表面上的凸峰为磨粒。SALISBURY等[3]利用二维傅里叶变换对三维砂轮表面结构进行研究，建立了适用于磨削过程仿真的砂轮表面模型。第三类是基于磨粒模型构建虚拟砂轮，即将磨粒模型按照一定规律排布到虚拟砂轮表面。CHEN等[4]先将磨粒阵列排布在三维空间中，然后给予磨粒随机位移，生成具有随机磨粒位置的虚拟砂轮。

在磨削研究中，常用的磨粒模型有球形、圆锥、圆台以及凸多面体。在第三类砂轮建模方法的相关研究中，基于凸多面体模型建模占有较大比重。凸多面体有四面体、六面体、八面体等简单的几何图形[5-7]，也有复杂的随机凸多面体[8-11]。随着计算机技术的快速发展，近年来采用凸多面体建模的虚拟砂轮研究日益增多。LI等[8]通过立方体与八面体相交的方法，生成具有金刚石磨粒特征的随机凸多面体磨粒。PELLEGRIN等[9]模仿磨粒在磨损过程中顶点和边缘位置先磨损的现象，采用随机截去空间凸多面体顶角的方法生成了随机凸多面体磨粒模型。宿崇等[10]通过球的随机切平面切割空间立方体的方法生成了随机多面体磨粒模型。邓朝晖等[11]采用基于球坐标的随机点产生空间平面切分实体的方法生成随机磨粒。

利用磨粒模型生成虚拟砂轮，关键是将磨粒排布在砂轮表面，在此过程中会涉及磨粒之间的干涉问题。少数研究为了简化模型，不考虑磨粒之间的干涉[6，12]，多数研究为了得到更具实际砂轮表面特征的虚拟砂轮，考虑了磨粒的干涉问题。对磨粒干涉问题的处理方法主要有两类：一类是限制磨粒的移动范围，使磨粒的移动范围不重叠；另一类是对磨粒进行碰撞检测，以避免磨粒之间出现干涉，大部分的磨粒干涉问题研究采用该处理方法。目前，虚拟磨粒干涉检测基本采用包围球碰撞检测方法[4，13-14]。

对于凸多面体，采用包围球碰撞检测磨粒干涉时存在包围球相互接触但磨粒间距过大的情况，这一现象影响了磨粒的空间位置分布，导致虚拟砂轮表面与实际砂轮表面存在一定的偏差。为解决该问题，本文提出一种基于凸多面体碰撞检测的虚拟砂轮建模方法，并与包围球碰撞检测方法进行对比分析，验证本方法的优越性。

1 随机磨粒模型

1.1 磨粒的生成

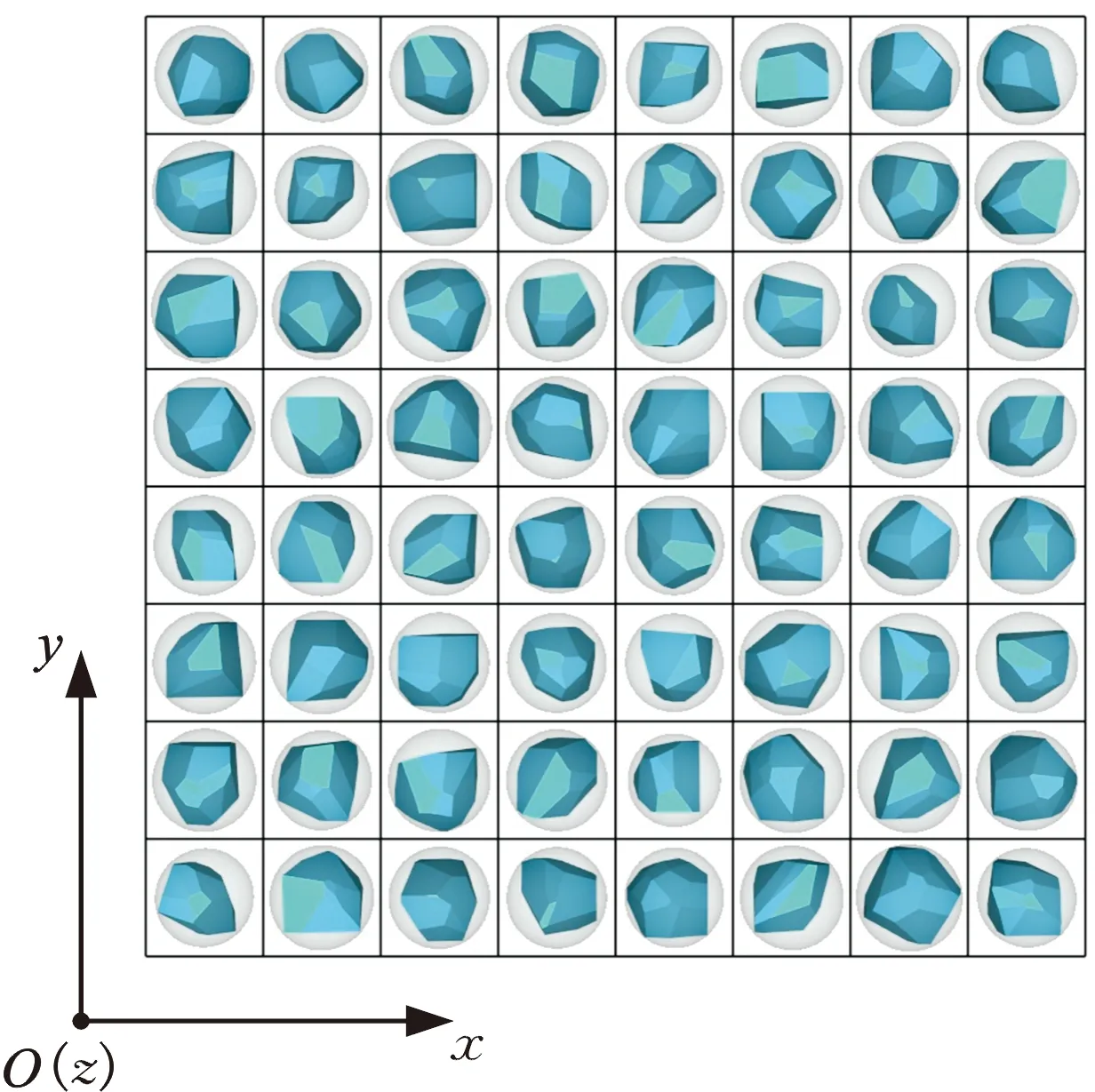
目前的磨粒形状除了球形、圆锥形之外，大多数为凸多面体，如四面体、六面体、八面体以及随机凸多面体等。造成磨削过程复杂的原因之一就是磨粒的随机性，砂轮表面有成千上万颗磨粒，这些磨粒在形状、大小、姿态上都各不相同。为更具一般性，本文采用文献[10]的随机凸多面体磨粒模型，该模型是利用球的随机切平面对立方体进行切割生成的。该模型的实现原理如图1所示，具体生成步骤如下：①建立棱长为l的立方体；②以立方体质心为球心，建立半径为r的球体；③在球体表面随机选取一点，以此点作球体的切平面对立方体进行切分，保留球心一侧的实体，去除另一侧实体；④重复步骤③，直至达到预设的切分次数。最终生成的磨粒为不规则的凸多面体，具有形状随机性。

图1 随机凸多面体磨粒模型示意图Fig.1 Random convex polyhedron abrasive model

1.2 磨粒的当量直径

在传统的磨削研究中，人们习惯将磨粒看作球形，因此经典的磨削理论采用磨粒直径表示磨粒大小，但由于凸多面体磨粒不是球形，并没有直径这一参数，故采用当量直径来表征磨粒大小。本文采用最小包围球(minimum enclosing ball，MEB)的直径作为凸多面体磨粒模型的当量直径，如图2所示。磨粒的最小包围球是能够包含磨粒的最小球体，具有唯一性。最小包围球一般应用于碰撞检测，可以粗略判断磨粒干涉情况。

图2 磨粒的最小包围球Fig.2 Minimum enclosing ball of abrasive grain

1.3 磨粒大小修正

通常采用粒度来划分磨粒直径大小。对于某一粒度的磨粒，其磨粒直径分布区间由筛选磨粒的筛网决定。磨粒先通过网孔较大的筛网，将大于该筛网孔径dmax的磨粒筛除。然后通过网孔较小的筛网，将小于该筛网孔径dmin的磨粒筛除，留下磨粒的尺寸范围为[dmin，dmax]。相关研究表明，磨粒的直径大小服从正态分布[15]，如图3所示。本文假设磨粒的直径服从正态分布，其概率密度函数如下：

(1)

(2)

式中，d为磨粒直径；μ、σ分别为磨粒直径的均值和标准差。

图3 磨粒直径分布的概率密度函数Fig.3 Probability density function of abrasive grain diameter distribution

根据正态分布的3σ原则，随机变量的值基本集中在[μ-3σ，μ+3σ]，认为μ-3σ和μ+3σ分别是随机变量取值的下限和上限，因此，磨粒直径的最大值、最小值、均值和标准差之间存在以下关系：

(3)

则磨粒直径的标准差为

σ=(dmax-dmin)/6

(4)

根据磨粒的直径分布，将1.1节的磨粒模型进行缩放变换，使磨粒模型的直径符合实际的磨粒大小。假设点(x，y，z)是磨粒模型上的点，则经过缩放变换后的坐标为

(5)

式中，d0为缩放前的磨粒模型直径。

2 砂轮模型

2.1 砂轮的磨粒率

因为磨削时主要是砂轮表层的磨粒参与切削，因此本文只建立单层磨粒的砂轮模型。首先，将砂轮的圆周面展开，建立坐标系Oxyz；然后，参考文献[4]中的方法，将磨粒按照等距离排布，使相邻磨粒球心的间隔为L，如图4a所示。这相当于将磨粒放入棱长为L的立方体中，并使磨粒的球心与立方体质心重合，如图4b所示。立方体体积与砂轮模型的磨粒率有如下关系：

V=Vg/Vcube

(6)

式中，V为磨粒率，即磨粒在磨具中占有的体积百分数；Vg为所有磨粒的总体积；Vcube为所有立方体的总体积。

(a) 磨粒阵列排布

超硬砂轮一般用浓度号表示磨粒的相对体积分数，可以根据浓度号的定义来换算出超硬砂轮的磨粒率。对于普通砂轮，磨粒率可按下面公式进行计算[16]：

V=2(31-S)/100

(7)

式中，S为砂轮的组织号。

凸多面体体积的计算比较复杂，本文采用最小包围球体积估算磨粒体积，虚拟砂轮中所有磨粒的体积计算公式如下：

(8)

式中，dk为第k个磨粒的直径；n为磨粒总数。

立方体个数与磨粒总数一致，所有立方体的总体积计算公式如下：

Vcube=nL3

(9)

将式(8)和式(9)代入式(6)，求解得到立方体棱长为

(10)

2.2 磨粒的随机位置

磨粒突出高度是非常重要的参数，它关系到磨削表面的形貌。有研究认为，磨粒突出高度服从正态分布，其均值和标准差分别如下[17]：

(11)

实际上，磨粒突出高度的取值范围存在上下限。本文假设磨粒突出高度的取值范围为(μh-cσh，μh+cσh)，其中，c为系数，决定了突出高度的上下限。

给予磨粒z轴方向上的随机位移使磨粒突出高度符合正态分布，移动后第(i，j)颗磨粒球心的z轴坐标为

(12)

在保持磨粒突出高度不变的情况下，给予磨粒一个Oxy平面上的随机移动，使磨粒的空间位置具有随机性。移动后磨粒球心的x、y轴坐标如下：

(13)

2.3 磨粒的碰撞检测

在真实的砂轮表面，磨粒之间并不存在干涉，因此需要对磨粒进行碰撞检测。传统的虚拟砂轮建模通常采用包围球碰撞检测方法，该方法要求任意两颗磨粒之间的中心距离大于或等于两颗磨粒的半径之和，即需满足如下关系：

(14)

对于凸多面体，采用包围球碰撞检测会存在较大的误差，如图5所示，当两磨粒的最小包围球接触时，两磨粒并未接触，磨粒间存在较大的间隙，而在真实的砂轮中，经常出现磨粒相互接触的情况，此时磨粒间隙小于磨粒的半径之和，所以用包围球检测方法检测凸多面体磨粒干涉已不适用。为使虚拟砂轮更加接近真实砂轮，本文采用凸多面体碰撞检测方法检测磨粒干涉状况。

凸多面体是由一系列平面包围形成的三维几何体，它所占的空间可用下式表示：

(15)

式中，(Ai，Bi，Ci)为磨粒第i个面的法向量，方向指向磨粒外部；(xi，yi，zi)为磨粒第i个面上的一点；m为磨粒的总面数。

(a) 包围球接触

式(15)中每个不等式表示的是以凸多面体某个面所在的平面划分的半空间区域。对于三维空间中的一点(x，y，z)，若满足式(15)，则该点位于凸多面体内部。因此，当检测两个磨粒是否干涉时，利用式(15)判断一颗磨粒上是否存在一点位于另一颗磨粒的内部，若存在这样的点，则两磨粒相互干涉，反之则不干涉。

2.4 虚拟砂轮模型生成

在磨粒排布时，对磨粒进行碰撞检测，若存在干涉，则重新给予磨粒随机位移直到磨粒之间不存在干涉为止。至此，得到砂轮表面展开时的磨粒坐标。最后，将磨粒坐标变换到砂轮的圆周面上，即得到最终的虚拟砂轮，其坐标变换为

(16)

式中，R为砂轮的半径。

虚拟砂轮生成流程如图6所示。生成虚拟砂轮主要分两个步骤：第一步是生成磨粒模型，第二步是磨粒排布。碰撞检测方法直接影响着虚拟砂轮的最终表面，是磨粒排布的关键步骤。

图6 虚拟砂轮生成流程图Fig.6 Flow chart of virtual grinding wheel generation

图7a所示为根据本文方法生成的虚拟砂轮。为便于观察磨粒干涉情况，对砂轮表面进行局部放大，如图7b所示，可以看到，磨粒位置具有随机性，相邻磨粒之间的间距较小，部分磨粒重叠，疑似干涉。为分析重叠磨粒是否干涉，对疑似磨粒干涉的区域进行再次放大，并调整到适当的视角，如图7c～图7e所示，可以看到磨粒之间仍存在极小的间隙，因此可认为磨粒之间并不干涉。这说明在图7b中，因为视角的原因，导致磨粒部分重叠在一起，实际上磨粒并未干涉。综上，凸多面体碰撞检测方法可以用于虚拟砂轮的建模。

3 对比分析

3.1 不同碰撞检测方法对磨粒位置分布的影响

本文提出的虚拟砂轮建模方法与传统的虚拟砂轮建模方法相比，主要区别为，本文方法采用凸多面体碰撞检测方法进行磨粒的干涉检测。本文对基于凸多面体碰撞检测方法和基于包围球碰撞检测方法生成的虚拟砂轮表面进行比较。虚拟砂轮的参数如下：磨粒尺寸150～180 μm；磨粒率20%～60%。

表1所列为基于两种碰撞检测方法在不同磨粒率下的虚拟砂轮表面。在20%磨粒率下，基于包围球碰撞检测(以下称为“原始方法”)的虚拟砂轮表面磨粒分布均匀，磨粒间距较大。而基于凸多面体碰撞检测(以下称为“改进方法”)的虚拟砂轮表面，磨粒的位置更具随机性，相邻磨粒间距更小，并且出现较大的磨粒间隙区。随着磨粒率的增大，单位面积上的磨粒数量增加，此时，原始方法的虚拟砂轮表面磨粒位置的随机性逐渐减小，当磨粒率达到40%时，其磨粒基本呈直线排布。这是因为当磨粒率较高时，磨粒间距L减小，若基于包围球进行碰撞检测，则留给磨粒随机移动的空间非常有限，因此磨粒呈直线排布。反观改进方法的虚拟砂轮表面，当磨粒率为40%时，磨粒位置仍具有很好的随机性。

实际上，砂轮具有较高的磨粒率，组织号为0时，砂轮的磨粒率高达62%。当磨粒直径都相等时，原始方法最高能生成磨粒率为52.4%的虚拟砂轮，此时磨粒直径与立方体边长相等，磨粒只能规则阵列排布，不具备磨粒位置的随机性，与实际砂轮表面不符。实际上，磨粒直径不可能都相等，因此原始方法生成的砂轮磨粒率要小于52.4%，无法达到较小组织号砂轮的磨粒率要求。如表1所示，包围球碰撞检测无法生成磨粒率为50%和60%的虚拟砂轮。而凸多面体碰撞检测允许包围球之间部分重叠，能生成更高磨粒率的砂轮。经仿真试验，该方法可以生成62%磨粒率的虚拟砂轮，即可以模拟最小组织号的砂轮。因此，凸多面体碰撞检测方法比包围球碰撞检测方法更适合虚拟砂轮建模。

表1 基于不同碰撞检测方法生成的虚拟砂轮表面对比

针对每一颗磨粒，计算与之相邻最近磨粒之间的中心距离，即该磨粒最小中心间距，统计结果如图8所示。可以看到，改进方法中最小磨粒中心间距的均值小于原始方法中最小磨粒中心间距的均值。这说明在改进方法下，磨粒的随机移动范围更大，能够形成更小的磨粒间距。当磨粒率增大时，两种方法的均值和标准差都减小，这是因为随着磨粒率的增大，磨粒的平均间距减小，导致磨粒可随机移动的范围减小。当磨粒率为40%时，原始方法的标准差很小，这说明磨粒间距的变化范围小，因此，在原始方法下磨粒近似呈直线排布。而此时，改进方法的标准差是原始方法标准差的2.6倍，说明改进方法的磨粒位置分布更加随机。

(a) 磨粒率为20% (b) 磨粒率为30% (c) 磨粒率为40%图8 磨粒最小中心间距统计Fig.8 Minimum distance of abrasive grain centers

3.2 虚拟砂轮表面与真实砂轮表面对比

根据本文方法生成虚拟砂轮表面，并与真实砂轮表面进行比较。虚拟砂轮的参数为：磨粒尺寸150～180 μm；磨粒率50%。

(a) 虚拟砂轮表面

图9为虚拟砂轮表面与实际砂轮表面对比图。图9a为虚拟砂轮表面图，图中相邻磨粒间距小，存在面积较大的磨粒间隙区(图中虚线包围区域)。该间隙区是由于磨粒随机移动之后产生的无规则的无磨粒区。图9b所示为真实砂轮表面，同样可以看到相邻磨粒间距小，也存在较大的无规则间隙区，这与虚拟砂轮的表面特征一致，说明基于凸多面体碰撞检测方法生成的虚拟砂轮表面与真实砂轮表面具有很高的相似性。

综上所述，基于凸多面体碰撞检测方法的虚拟砂轮表面具有真实砂轮的表面特征。