两尺度Duffing 系统的动力吸振器减振研究1)

万洪林 * 李向红 * 2) 申永军 ** 王艳丽

* (石家庄铁道大学数理系,石家庄 050043)

† (石家庄铁道大学机械工程学院,石家庄 050043)

** (石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043)

引言

破坏性的振动往往会导致机器本身性能、可靠性降低和产生噪声污染等问题,振动系统附加动力吸振器是常见的减振方式之一.动力吸振器(dynamic vibration absorber,DVA)是一种通过与系统耦合进而吸收主系统振动能量,抑制其大幅振动的装置[1].1909 年由Frahm[2]提出了无阻尼动力吸振器,其特点是只针对窄带频率有效.基于此,Ormondroyd 等[3]提出加入阻尼元件设计了经典的Voigt 式动力吸振器,相较无阻尼动力吸振器其减振效果更好,适用范围更大.Ren[4]设计了一种新型的接地式动力吸振器,进一步提高了吸振器的减振效果.随后,一些学者又对动力吸振器展开了一系列的改进与提高.徐振邦等[5]研制了一种随外部激励频率变化调节吸振器几何参数进而改变其固有频率的机械式频率可调吸振器.作者团队在Voigt 型动力吸振器的基础上进行了部分改进,如彭海波等[6]设计了一种附加接地负刚度的新型动力吸振器模型;隋鹏等[7]设计了一种含惯容和接地刚度的新模型.相较于传统模型的减振效果,新型吸振器的减振效果更好,同时还拓宽了减振频带.

参数激励存在于许多工程领域中,其非线性动力学和振动控制问题受到很多学者的关注.丁虎[8]分别通过两种数值方法研究了两种经典边界条件下轴向变速黏弹性梁参激振动的稳定性问题.顾伟等[9]研究了预变形变转速叶片在参数激励下的非线性动力学特性.马磊等[10]研究了船舶受参数激励导致的大幅度横摇运动问题,提出加入减摇鳍控制器来降低参数激励对系统的危害.路一鸣[11]研究了受参数激励的超长斜拉索振动特性及耦合黏滞阻尼器后的控制效果.Yang 等[12]提出调整旋转柔性盘系统所受参数激励位置相位角来抑制其横向振动的方法.

作为一个经典的非线性模型,Duffing 型振子的振动控制问题被广泛研究.Wang 等[13]研究了将动力吸振器应用到经典Duffing 型旋翼与甲板耦合系统中,并得出吸振器的最优放置位置.Taghipour 等[14]研究了Duffing 型Jeffcott 转子系统耦合动力吸振器减振问题.Bronkhorst 等[15]将含有黏弹性元件的动力吸振器耦合到Duffing 系统来抑制系统振动.刘彬等[16]向轧机辊系的Duffing 型模型中加入吸振器,可以有效抑制轧机辊系垂直振动.Yabuno[17]提出向受参数激励的Duffing 系统中加入线性反馈和非线性反馈来抑制系统主共振影响.Li 等[18]向固有频率与参数激励频率为1:1 的混沌Duffing 系统中加入高斯白噪声相位来抑制系统混沌.

目前各领域研究的大多是共振情形下的振动控制问题.事实上,实际工程系统常常会受到不同频率干扰的外界因素影响.当激励频率与系统固有频率存在量级差异时,系统变为了多尺度系统,此类系统存在复杂的振动,比如一直处于激发态的大幅高频振动、也有激发态和沉寂态共存的簇发振动(也称为混合模式振动)[19].例如,Simo 等[20]研究了受正弦低频激励的Duffing 振子与刚性梁耦合的机电设备中不同参数下表现出的簇发现象.文献[21-22]研究了周期激励下多尺度水轮机系统表现出的簇发特性.Zhang 等[23]研究了低频外部激励下准零刚度隔振器系统表现出的簇发振动现象.针对系统表现出的复杂簇发振动模式,早期的研究方法主要侧重于实验、数值模拟等方法.直到Rinze 等[24]将快慢动力学分析方法引入簇发现象的分析中.Izhikevich[25]将分岔理论引入簇发现象产生的机理研究中,相关学者才对一系列不同尺度系统的簇发现象与机理展开研究.陆启韶等[26-27]利用快慢分析法对多尺度神经元系统表现出的同步簇放电振荡进行研究,并揭示其转迁机制.文献[28-30]分别对具有多频、高维、非线性等特点的多尺度模型进行分析,结合快慢分析法对其表现出的簇发现象及其产生机理展开了一系列研究.Li 等 [31]研究带有慢参数激励的单自由度Duffing 系统,发现了一种新型的周期混沌运动,此类运动具有明显大幅张弛振动行为.Birkoben等[32]研究了原混沌蔡氏电路加入忆阻器的簇发现象,这种振动模式是轨线经过慢流形上的Hopf 分岔点发生大幅振荡组成的.

目前,针对具有多尺度耦合系统的研究大多集中在簇发振动现象与机理分析.然而,此类系统中存在的振动往往不仅有大幅振动,而且也存在高频振动,这些振动对系统的破坏作用不容忽视,因而深入研究多尺度耦合系统的振动控制问题是非常必要的.本文将考虑低频参数激励下Duffing 系统耦合吸振器的减振问题,基于快慢分析法和数值计算方法,重点探讨耦合吸振器后整个系统的分岔机制、减振效果与机理、快慢效应与减振的密切关系等.

1 系统方程与稳定性分析

1.1 系统方程

具有参数周期激励的Duffing 系统为

耦合吸振器后的动力学模型为

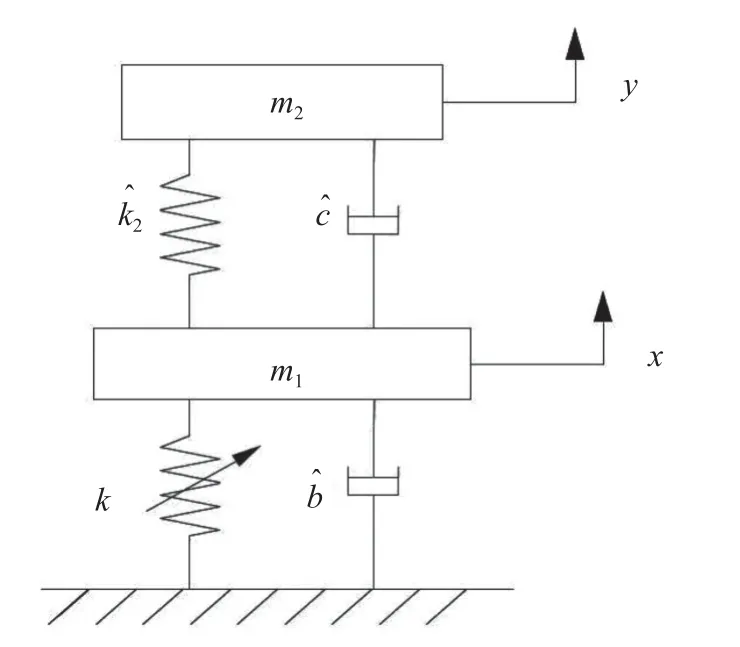
当参激频率较小即 ω1≪ 1 时(1 为系统参数取值的最大量级),参数激励量级相较于其他参数量级取值很小时,参数激励为系统的慢过程,系统(3)和系统(4)为两尺度耦合非自治系统.

为了深入研究参数激励部分对系统的影响规律,依据参考文献[30],令F=k1cos(ω1t).在固有频率振动周期 ψ 内,取t在[t0,t0+ψ] 内变化,则F在内变化,由于 ω1很小导致F t0与非常接近,因此在时间段 ψ内,F可以近似看作常数,相应的非自治系统转化为自治系统.

式(3)和式(4)变为如下式(5)与式(6)

其中,x1和x2是主系统位移和速度

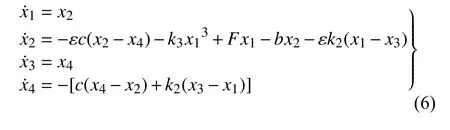
其中,x1和x2是主系统位移和速度,x3和x4是吸振器位移和速度.

显然系统(5)和系统(6)形式上为典型的自治系统,同时与非自治系统(3)与系统(4)的振动密切相关.这是因为系统(3) 与系统(4) 的参数激励项k1cos(ω1t)在[ −k1,k1] 内周期性变化,对应其自治系统(5)和系统(6)中,表示F有参数范围 [ −k1,k1].F的变化将可能导致自治系统(5)与系统(6)的稳定性发生变化或者产生分岔行为,而自治系统稳定性变化和分岔行为,将对非自治系统(3)与系统(4)的振动行为产生较大影响.具体的说如果自治系统(5) 与系统(6) 在以上参数范围内具有稳定(不稳定)平衡点,则非自治系统(3)与系统(4)的振动具有明显的收敛(发散)趋势.如果自治系统中的F在[−k1,k1]上有分岔行为,往往导致非自治系统(3)与系统(4)的振动轨线发生改变.另一方面,激励频率ω1的大小决定参数F的变化速度.该变化过程越慢,自治系统的稳定性和分岔影响非自治系统的振动行为越明显.另外F周期性的变化,会使得自治系统对非自治系统的影响周而复始的发生.因此研究自治系统中F为分岔参数时系统的动力学,对深入研究整个非自治系统的振动行为具有重要意义.

1.2 稳定性与分岔分析

下面考虑平衡点稳定性,其派生线性系统的特征值方程为

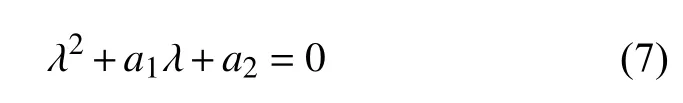
在点 (0,0) 的特征系数为

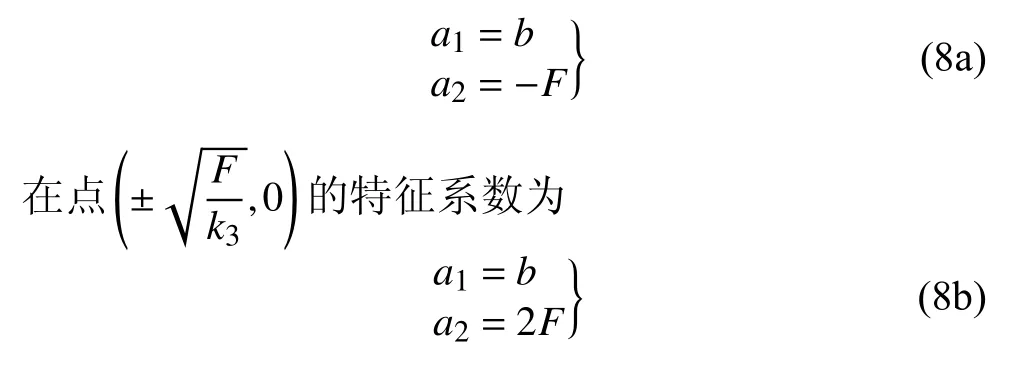
在不同平衡点处的特征值如下

其中

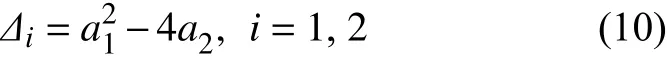
虽然平衡点不同,但影响特征值实部的均为参数b和F.当a1≥0,∆1<0,∆2<0 时,两个平衡点的特征值为一对实部非正的共轭复数,平衡点稳定.a1<0,平衡点不稳定.

取定参数b=0 时,系统(5)分岔图如图2 所示,其中F=0 时,系统产生叉形分岔,实线为稳定平衡点,虚线是不稳定平衡点.

图1 耦合线性吸振器的Duffing 系统Fig.1 Duffing system coupled with linear vibration absorber

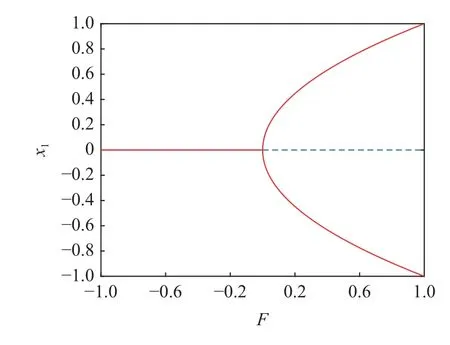
图2 系统(5)关于 F 的分岔图Fig.2 The bifurcation diagram of system (5) with respect to F

其派生线性系统的特征方程为

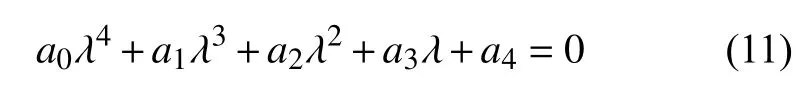
在 (0,0,0,0) 的特征方程系数为

在平衡点特征值实部的表达式形式为

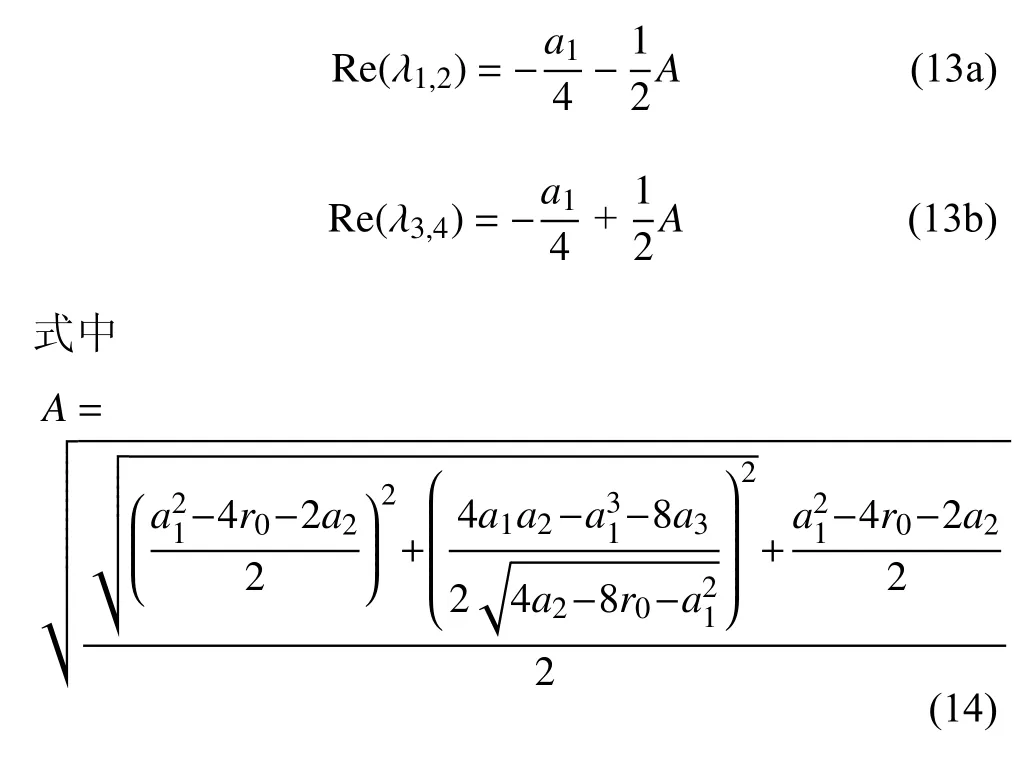
其中,r0取值见附录1.

由特征值实部的表达式可以发现,特征值实部与系统(5)的参数b,F和系统(6)的参数c,k2和 ε有关.当参数满足 α1≥0,α2≥0,∆1<0,∆2<0 时,平衡点的特征值实部均小于0 时,平衡点稳定.当参数满足 α1<0 或 α2<0 时,平衡点不稳定.

取定 参数c=0.4,k1=1,k2=1.5,k3=1,ε=0.1,ω1=0.01,b=0,给出系统(6)分岔图如图3 所示,其中F=0 时,系统产生叉形分岔,实线为稳定平衡点,虚线是不稳定平衡点.虽然叉形分岔与未加吸振器的自治系统一样,但是平衡点的稳定性具有明显不同,并在下文中详细阐述.

图3 系统(6)关于 F 的分岔图Fig.3 The bifurcation diagram of system (6) with respect to F.

2 减振效果与机理分析

下面研究在相同参数c=0.4,k1=1,k2=1.5,k3=1,ε=0.1,ω1=0.01,b=0下,系统(3) 和系统(4)不同的动力学行为,从而得到耦合吸振器后的减振效果,并给出系统减振机理解释.

2.1 减振效果

图4(a)为系统(3)位移时间历程图,此时系统处于大幅高频振动的发散状态,即系统一直呈激发态振动,并且轨线振幅趋于增大.图4(b)是耦合吸振器后系统(4)的位移时间历程图,发现加入吸振器之后,系统的高频振动大幅降低,出现小幅高频的激发态与沉寂态相结合的混合振动模式,即簇发振动.图5(a)为系统(3)相图,图5(b)为耦合吸振器后系统(4)的相图.从相图中很明显看出,加入吸振器后,主系统位移振幅降低近50%,速度振幅大幅降低,由2 衰减到0.1.

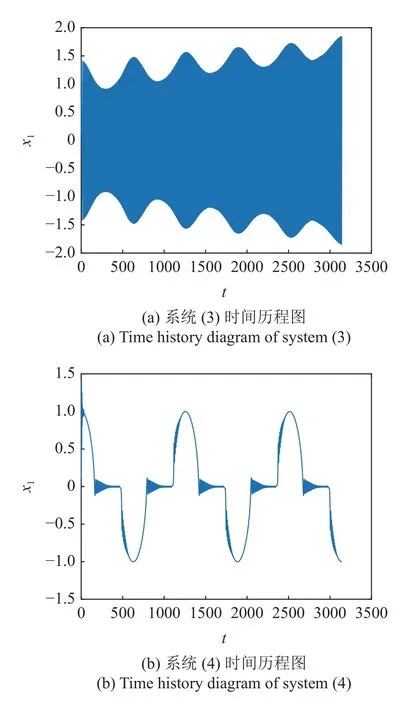
图4 位移时间历程图Fig.4 Displacement time history diagram

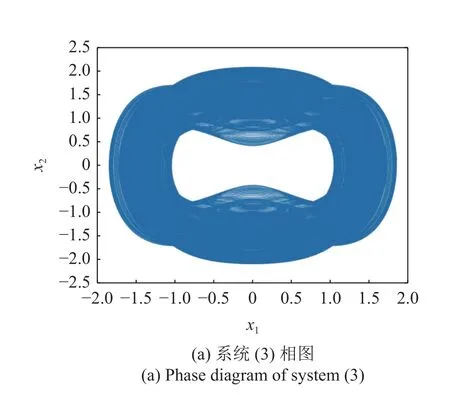
图5 相图Fig.5 Phase diagram

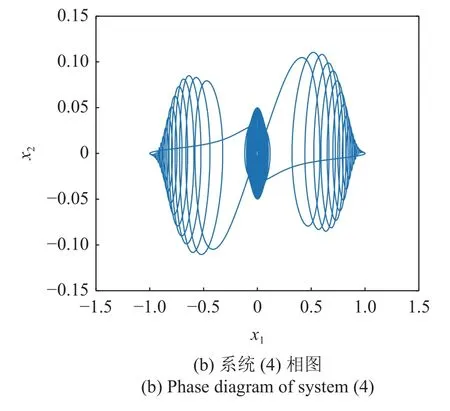
图5 相图(续)Fig.5 Phase diagram (continued)

2.2 减振机理分析

事实上,自治系统平衡点的稳定性对相应非自治系统振动模式的影响是非常明显的.耦合吸振器之后,系统平衡点的稳定性变化,是减振的重要原因.下面给出系统(5)与系统(6)平衡点稳定的变化,导致系统(3)与系统(4)振动的变化,从而达到减振效果的机理分析.平衡点特征值实部最大值随F的变化如下图6 和图7 所示.红色虚线代表原始系统特征值实部,黑色虚线代表耦合吸振器系统的特征值实部.

图6 (0,0) 与 (0,0,0,0) 特征值实部最大值Fig.6 The maximum real part of the eigenvalues of (0,0) and (0,0,0,0)

当F<0 时,(0,0) 平衡点特 征值为一对实部为0 的共轭纯虚根,平衡点类型为中心.加入吸振器之后,(0,0,0,0) 平衡点特征值为两对共轭复根,特征值实部最大值小于0,平衡点类型为渐进稳定的焦点,这使得系统(4)的轨线明显的被平衡点吸引,因而振动幅值降低.

F>0时,平衡点特征值为一对实部为0 的共轭虚根,平衡点类型为中心.加入吸振器之后,平衡点特征值为两对共轭复数,特征值实部最大值小于0,为渐进稳定的焦点,如图7所示.耦合吸振器后的系统(6)特征值绝对值远远大于耦合前系统(5),导致系统(4)轨线被平衡点强烈吸引,从而振动幅值大大低于原系统(3).

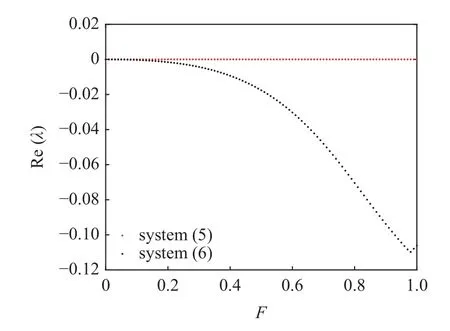
图7 与 特征值实部最大值Fig.7 The maximum real part of the eigenvalues of and

总之,耦合吸振器后,中心平衡点演变为渐进稳定的焦点.导致系统(3)的发散运动变为系统(4)的周期运动,同时位移振动幅度和速度大小都有显著减小,从而主系统大幅高频的发散振动得到抑制.这一机理将在后面的分析中详细展示.

2.3 焦点式簇发产生机理

为了深入理解上述减振机理,并清楚展示自治系统(6)稳定性与分岔是如何影响非自治系统(4)的振动行为,采用快慢分析和转换相图进行详细阐述.转换相图指的是系统(3)与系统(4)状态变量随慢变参激过程量变化而变化的过程,如图8 所示,状态变量x1随慢变过程F=cos(0.01t) 变化的相图.随着时间的增加,F在 [ −1,1] 之间缓慢周期性变化进而调控变量x1的运动.

快慢分析,即将慢变量F作为自治系统的调节参数,并给出自治系统的单参数分岔图,即图3 所示的x1与F的分岔图.将状态变量x1与慢变量F的转换相图图8 和分岔图图3 叠加得到图9(a).下面将图9(a)分成两部分,一部分是如图9(b)所示的随F增加,状态变量x1的变化情况;另一部分是图9(c)中随F减小状态变量x1的变化情况,图中的箭头表示轨线运动的方向.通过观察叠加图中的现象,来揭示系统中振荡产生的动力学机理.

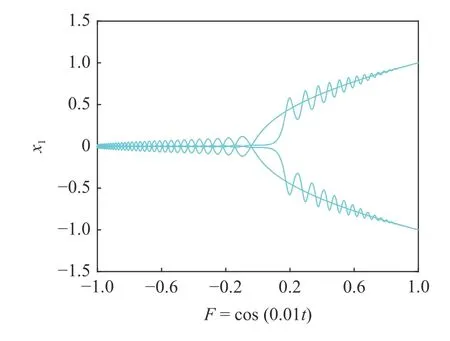
图8 系统(4)转换相图Fig.8 Transformed phase portrait of system (4)

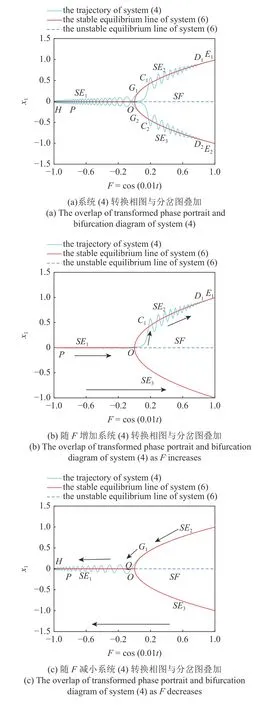
图9 簇发现象的产生机理Fig.9 Generation mechanism of bursting phenomenon.

现在详细描述一个周期的运动情况,假设轨线从P点出发,加入吸振器后的系统(4)轨线受到其相应自治系统(6)稳定平衡线的吸引,将沿着稳定的平衡线SE1向右平稳运动,当轨线经过点O时系统(6)发生叉形分岔,系统(4)轨线受到稳定平衡线的吸引后跳跃到平衡线SE2上的点C1.因为SE2上的点是稳定焦点,所以轨线将围绕SE2产生较大幅值的振动形成激发态.在持续受到稳定平衡点的吸引下,振幅逐渐减小直到在D1点时与平衡线近似重合,激发态消失.当慢变量F=cos(0.01t) 到最大值E1(F=1)后向左折返,然后沿着稳定平衡线向左运动,系统一直处于沉寂态.轨线运动到G1点时由于叉形分岔临界点点O,又由于稳定平衡线SE1的吸引,使得轨线到达点Q,表现为围绕SE1振荡的激发态且振幅逐渐减小,当慢变量F=cos(0.01t) 达到最小值(F=−1)后向右运动,并逐渐与平衡线重合进入沉寂态,运动到点P后完成一个周期的运动,下一个周期将沿着平衡线SE3做类似的运动.因为激发态和沉寂态与平衡线上的稳定焦点密切相关,所以这个过程也称为点-点型簇发.

下面给出未加入吸振器时的振动分析.图10 是系统(3)转换相图与平衡线的叠加图,图10(a)是F增大方向,图10(b)是F减小方向.可以看出,系统(3)轨线在围绕SE1-SE2-SE3振荡的过程中,由于系统(5)的SE1-SE2-SE3平衡线上的点都是中心,对轨线的吸引力很弱,导致整个系统(3)处在高频大幅振动的激发振动状态.

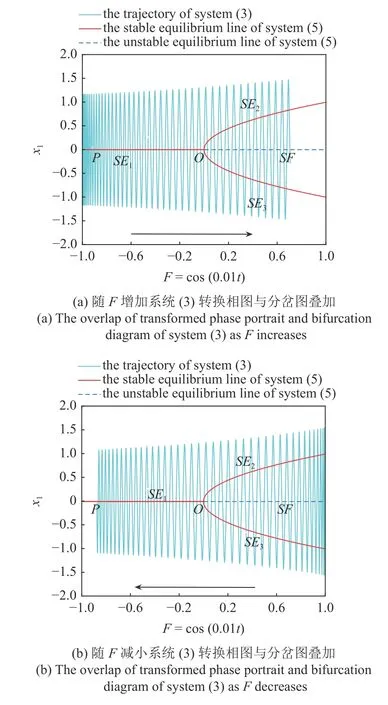
图10 系统(3)转换相图与分岔图叠加Fig.10 The overlap of transformed phase portrait and bifurcation diagram of system (3)

加入吸振器自治系统平衡线类型发生改变,渐进稳定的平衡线SE1-SE2-SE3吸引性明显增强,导致非自治系统轨线的运动发生变化,进而系统振动幅值得到抑制.另一方面,叉形分岔使得自治系统多个稳定吸引子共存,导致非自治系统轨线在不同稳定吸引子之间跳跃.由此可见,当参数激励项为缓慢过程时,其自治系统的动力学行为,对激励系统的振动具有明显的控制调节作用.

3 参数激励对吸振器减振的影响

当参数激励在一定范围内发生变化后,加入的线性吸振器能否对系统(3)仍有减振效果需要进一步探讨.因此,本节分析了当参数激励幅值k1和频率ω1发生变化后,加入的吸振器对系统(3)的减振效果.

3.1 参数激励幅值 k1

参数c,k2,k3,ε,ω1和b与第2 节取值相同.改变激励幅值k1,讨论当系统(3)受到幅值逐渐增大的参数激励时,吸振器对系统(3)振动的抑制效果.

图11 和图12 分别为参数激励幅值k1取0.1 和10 时,系统加吸振器前后的位移时间历程.图11(a)展示了系统(3)以大幅高频的形式振动,并且有缓慢的发散趋势.图11(b)为耦合吸振器后主系统位移的振动,系统的大幅高频振动逐渐演变为振幅收窄的振动,主系统振幅下降20%左右,主系统发散振动得到抑制.当激励幅值取为10,从图12(a)中可以看出系统以大幅高频模式振动,处于明显的发散状态.图12(b)可以看出,加入吸振器后系统呈现微幅高频和大幅低频的混合模式振动,发散状态得到明显抑制,振幅下降60%左右,此时吸振器的减振效果非常明显.从以上发现吸振器可以很好的抑制随着参数激励幅值增大导致的大幅振动.

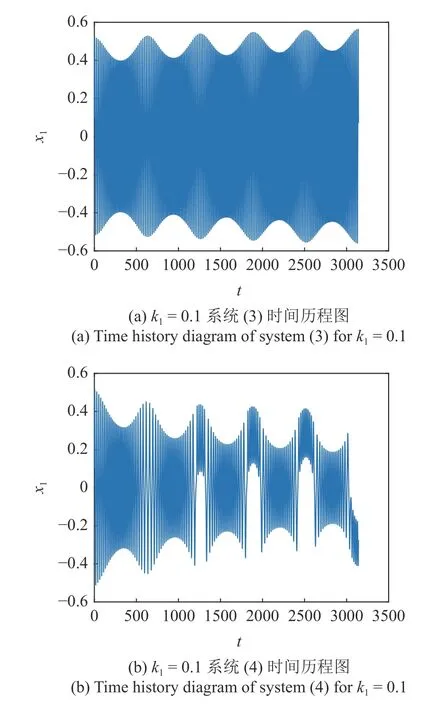
图11 参数激励幅值 k1=0.1 位移时间历程图Fig.11 Displacement time history diagram for parameter excitation amplitude k1=0.1

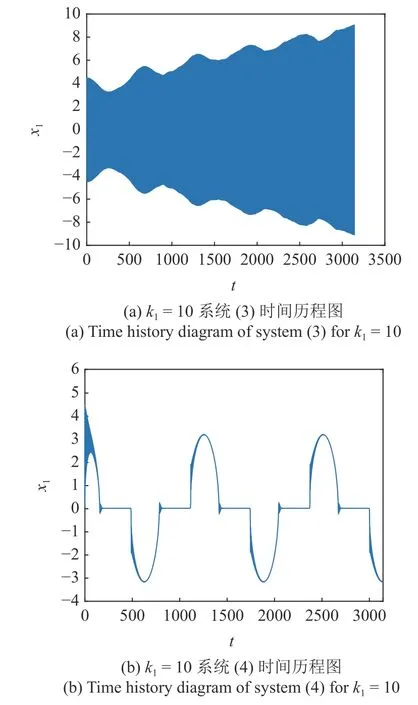
图12 参数激励幅值 k1=10 位移时间历程图Fig.12 Displacement time history diagram for parameter excitation amplitude k1=10

另一方面,从图4(a)与图12(a)对比可以看出,未加入吸振器的系统振动处于高频大幅振动状态,此时整个系统一直处于激发态,没有沉寂态.加入吸振器后系统呈现小幅激发态与沉寂态交替出现的张弛振动(簇发振动),从而达到减振效果.由此可见由单一振动模式向混合振动模式转变是减振的一种表现形式.

自治系统的稳定吸引子对非自治系统轨线的调控范围 [ −k1,k1] 显然与参数激励幅值k1有关.图13(a)和图13(b)分别为参数激励幅值k1取0.1 和10 时,非自治系统(4)转换相图与自治系统(6)分岔图的叠加.尽管红色平衡线上的点均为渐进稳定的焦点,但对轨线的收敛效果却有很大的差异.其原因是当激励幅值k1取0.1 时,非自治系统(4)轨线受自治系统(6) 的平衡线上渐进稳定焦点的吸引范围在[−0.1,0.1] 之间;当激励幅值k1取10 时吸引范围增大为 [ −10,10].非自治系统(4)轨线受自治系统(6)稳定平衡线吸引的调控范围增大,导致其大幅振动的轨线有足够的范围收敛到渐进稳定的平衡线上,因而响应幅值明显降低,吸振器的减振效果也更加明显.

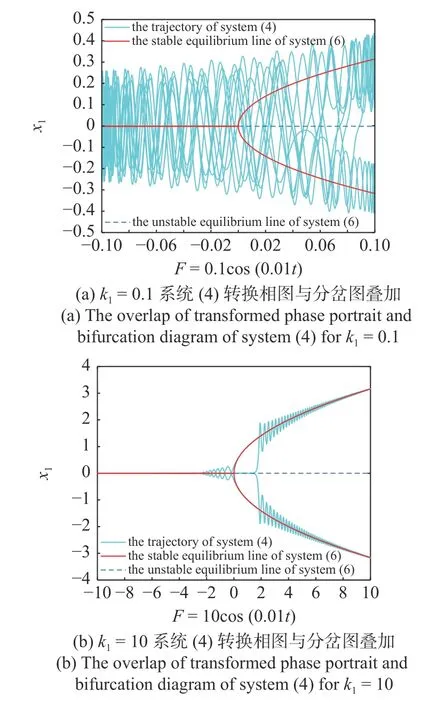
图13 系统(4)转换相图与分岔图叠加Fig.13 The overlap of transformed phase portrait and bifurcation diagram of system (4)

3.2 参数激励频率 ω1

参数c,k2,ε,k1,k3和b与第2 节取值相同.改变参数激励频率 ω1,讨论系统(3)受到不同频率的参数激励时,吸振器对系统(3)的减振效果.

给出 ω1分别取0.02 和0.1 时加入吸振器前后系统(3)与系统(4)时间历程图的叠加图,如图14(a)和图14(b) 所示.可以发现,当参数激励频率 ω1从0.02 增大到0.1 时,系统(3)的轨线均呈发散的趋势,但是系统(4)的轨线均呈周期性簇发振动,且幅值明显小于系统(3)的幅值.说明在较大的参激频率范围内,线性吸振器都可以有效的抑制主系统的振动.

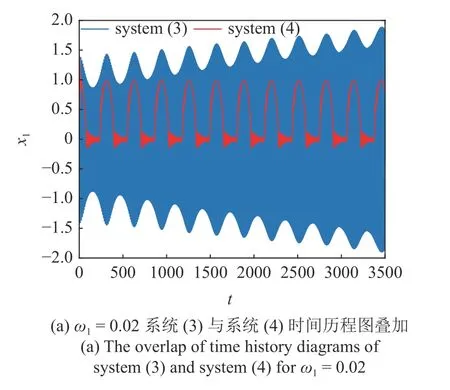
图14 系统(3)与系统(4)时间历程图叠加Fig.14 The overlap of time history diagrams of system (3) and system (4)

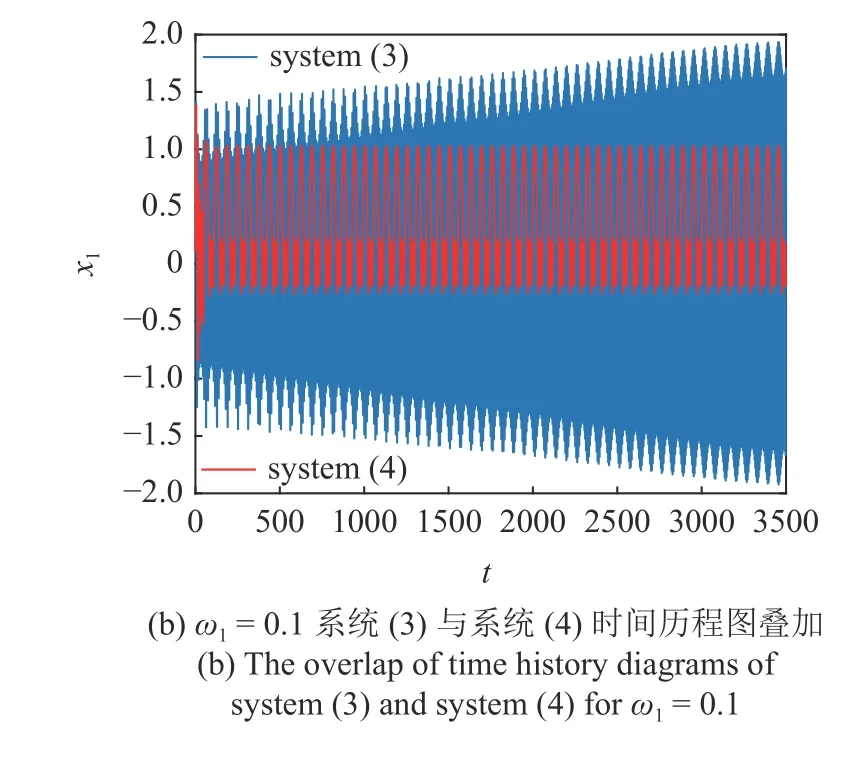
图14 系统(3)与系统(4)时间历程图叠加(续)Fig.14 The overlap of time history diagrams of system (3) and system (4) (continued)

4 结论

本文研究了线性吸振器对低频参激下两尺度耦合Duffing 系统的振动控制.发现主系统的大幅高频发散振动,在耦合吸振器后出现了典型的激发态和沉寂态耦合的混合簇发振动(混合振动),且振动幅值明显降低.因而得出单一高频振动模式向混合振动模式转变,是系统振动抑制的一种表现形式.基于自治系统与非自治系统动力学行为的相关性,结合快慢分析给出了减振机理解释.通过比较耦合吸振器前后系统的稳定性、时间历程图、相图和特征值实部情况发现主系统响应呈现出围绕中心大幅高频的发散振动,在耦合线性吸振器后,转变为围绕渐进稳定的焦点的张弛振动,主系统的振动在很大程度上得到抑制.其中自治系统平衡点稳定性增强是非自治系统减振的重要原因之一.另一方面,虽然耦合吸振器前后系统均发生叉形分岔,自治系统多个吸引子共存,但由于吸振器的加入,自治系统平衡线对非自治系统轨线的吸引性增强,轨线在不同吸引子之间的跳跃次数减少,是减振的另一个重要原因.研究还发现,参数激励幅值越大,吸振器的减振效果越好.在较大的参数激励频率范围内,线性吸振器对系统振动都有明显抑制效果.

附录

根据费拉里公式,系统(6)的特征方程(11)等价于