临近空间大气密度时空扰动规律及建模研究

曾丹丹 万田 李帅辉

(中国科学院力学研究所高温气体动力学国家重点实验室,北京 100190)

(中国科学院大学工程科学学院,北京 100049)

引言

临近空间通常是指20～120 km 高度范围的大气空间,该区域是高超声速飞行的重要区域.大气密度是飞行器空气动力分析的输入参数,研究大气密度及其变化规律对临近空间开发利用和临近空间飞行器能源动力的优化设计具有重要意义.

常用的大气探测手段有气球[1-2]、地基雷达[3-5]、探空火箭[6]和卫星观测[7-9]等.不同探测方法具有不同的时空覆盖特性;相对低空大气,临近空间高层大气探测难度较高,探测手段较少.随着多种卫星遥感探测技术,如掩星探测技术[10-11]和临边辐射测量技术的发展[12],卫星观测逐渐成为获取全球尺度大气参数的有效途径.2001 年12 月7 日,美国NASA 发射的TIMED 卫星上搭载的SABER 探测器,通过临边测量15 μm 波段和4.3 μm 波段的 CO2红外热辐射,可以反演获得大气温度及密度廓线,首次实现了平流层至低热层(14～108 km)大气密度的全球连续测量.

通过探测大气特性参数,掌握并预测大气特性参数分布及其变化规律是大气研究中的重要课题.在多年积累的数据基础上,目前已形成便于使用的经验模型,常用的如美国标准大气USSA-76 模型[13]和NRLMSISE-00 模型[14-16]等.USSA-76 模型代表了中等太阳活动期间,中纬度地区由地面到1000 km高度范围的大气平均状况.NRLMSISE-00 模型[15]是美国海军研究实验室 2000 年发布的大气经验模型,主要基于卫星和地基雷达的观测数据.NRLMSISE-00 模型考虑了时空、太阳辐射及湍流输运等因素对温度剖面的影响,在温度基础上获得密度.与USSA-76 模型相比,NRLMSISE-00 模型考虑了时空扰动的影响,具有更高的预测精度.然而,使用NRLMSISE-00 模型时需要知道太阳活动及地磁活动指数,这两个参数具有一定的不可预测性,增加了NRLMSISE-00模型工程应用的难度.随着探测数据的进一步积累,人们发现常用经验模型与实测数据之间存在较大偏差,尤其是高层大气[17-21].如在对低纬度大气环境的219 次掩星扫描测量中发现[19],在70～110 km 范围内,测量得到的平均密度可比NRLMSISE-00 模型低50%.文献[22]综述了热层大气密度模型的修正研究,但是对临近空间大气模型的修正研究则相对较少.文献[23]以TIMED/SABER 数据为基准,对NRLMSISE-00 模型预测的密度进行线性修正.文献[24]则参考TIMED/SABER 数据,对临近空间大气温度廓线进行了建模研究.本文将基于TIMED/SABER 的密度数据,首先评估太阳活动和地磁活动对临近空间大气密度的影响幅度;其次,结合工程应用特点,重点研究临近空间大气密度随时空因素如纬度、地方时和季节的变化规律,对扰动模式和扰动幅度进行全面的分析.在此基础上,根据测量数据对临近空间大气密度的时空变化特性开展建模研究,以期提高经验模型对大气密度的预测精度,满足高超声速航天器能源动力设计的精细化要求.

1 数据来源和分析方法

1.1 数据来源

TIMED 卫星轨道高度约625 km,轨道倾角为74.1°,轨道周期约1.6 h,轨道沿纬圈缓慢进动,每天进动约12 min.SABER 探测仪每天探测剖面约1400 个.本文采用SABER V2.0 版本密度数据,该版本考虑了70 km 以上大气非平衡辐射特征.SABER的直接探测量为大气红外辐射亮度,而辐射亮度与辐射气体分子数密度及温度有关,因此可通过辐射亮度反演得到辐射活跃分子的数密度及大气温度.SABER 数据采用了两种方法反演获得大气温度.第一种方法利用WACCM 模型获得大气中的CO2体积分数,在此基础上,利用CO2的15 μm 波段辐射亮度数据获得大气温度;第二种方法利用CO2的15 μm和4.3 μm 辐射波段辐射数据反演得到CO2体积分数及大气温度.在70～110 km 高度,白天温度数据为两种方法反演的温度平均值;其他情况,温度数据由第一种方法获得.在温度基础上,通过气体状态方程,即可得到大气密度.根据文献结果[25],SABER V2.0 的温度数据总误差在80 km 为2.3 K,90 km 的总误差为5.4 K,100 km 总误差为8.4 K.忽略压强误差,根据理想气体状态方程,可知密度的相对误差等于温度的相对误差,即密度的相对误差在100 km 约为5%.有较多文献对比了SABER 温度剖面与其他测量方法如落球[26]、掩星[9,27]和地面雷达[28-30]的温度数据结果.如,15～55 km 范围内,SABER 数据与COSMIC 掩星数据,相对偏差小于3 K[9];中间层中部,SABER 温度与瑞利散射雷达测量数据低2 K[30].因其高测量精度和时空覆盖范围上的优势,SABER 数据被广泛用于研究平流层至低热层大气运动的能量交换和动力学过程[31-35].

本文采用的SABER 密度数据高度范围为14～108 km,纬度范围为主半球的82°到副半球的54°,每60～ 63 天交换一次主副半球.垂直分辨率为2 km,水平分辨率为400 km.本文分析了从2002 年1 月到2021 年5 月的所有数据.

1.2 分析方法

根据温度垂直结构,地球大气层可自下至上分为对流层、平流层、中间层、热层.对流层顶高度大约为10～15 km 之间,平流层顶高度一般为45～55 km 之间,中间层高度一般在80～90 km 之间.因此,14～108 km 大气包含平流层、中间层、低热层,该范围内大气密度受下边界对流层,上边界热层,以及外部能量输入如地面辐射、太阳辐射和太阳风的影响.部分参数本身具有确定性,如地球自转和公转引起的地方时、日期、纬度和高度因素.另一些参数则具有相当的不确定性,如太阳辐射能量的强弱、太阳风的强弱、对流层湍流运动的输运等.太阳活动整体上以11 年为周期,高度越高,太阳活动对密度影响越大.表1 对比了80～ 100 km 高度太阳活动对全球平均密度的影响.2002 和2008 年分别对应太阳活动强、弱的年份,F10.7 指数的全年平均值分别为180 和69.表中全球密度数据为本文统计结果.从表1 可以看出,80,90,100 km 高度,全球平均密度在太阳活动弱年比太阳活动强年分别小4.88%,7.31%,12.9%.根据后文分析结果可知,相对其他因素如纬度等,太阳活动对本文高度范围内的大气密度影响相对较小.引起密度扰动的时空因素包括纬度、经度、地方时、日期.密度随经度的变化体现了行星波的影响[36-37].随着长时间发展,行星波的影响具有较大不确定性,因此本文的密度时空变化规律研究仅考虑纬度、日期和地方时因素.

表1 80,90,100 km 高度,太阳活动强(2002)、弱(2008)年份的密度Table 1 At altitudes 80,90,100 km,the global mean density for years with higher solar activity (2002) and lower solar activity (2008)

假设密度 ρ 是高度z、纬度 ϕ、地方时t和日期d的函数,即 ρ=ρ(z,ϕ,t,d).本文中 ρ (z,ϕ,t,d) 是高度z上,ϕ ±5◦,t±1 h,d±5 范围内所有密度数据的平均值,即

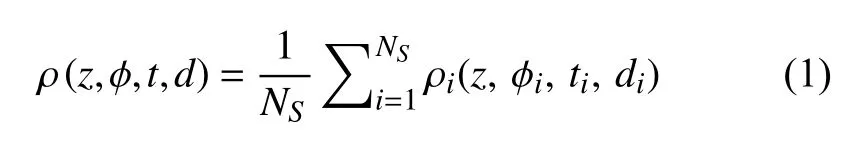
式中,ρi是满足 | ϕi−ϕ|≤5◦,|ti−t|≤1 h ,|di−d|≤5 条件的第i个密度数据,NS为满足该条件的样本总数.为避免样本数过少造成的不确定性,删除样本数少于10 的格点.样本数大于10 的格点有4666 个,这些格点的平均样本数为2111.作者对比了样本数下限为10 和50 的时空扰动规律,结果显示两者差别很小.

为简明起见,下文书写在不引起岐义时省略自变量z,如 ρ (ϕ,t,d) 默认指特定高度的密度.密度随维度“a”的变化用 ρa表示,在维度“b”上的平均则用 〈·〉b表示,“a”和“b”可以是一维或多维空间.特定高度的全球平均密度

密度随纬度的变化关系可写成

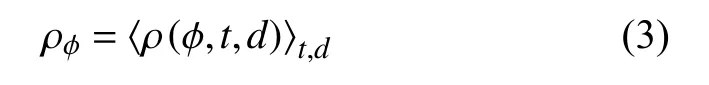
随地方时及纬度的变化

依此类推,可得到密度随其他一维或二维参数的变化.考虑到地球的球形特征,纬度平均特指权重为cosϕ 的加权平均.密度随“a”的变化幅度用标准差 σa衡量,例如,纬度引起的变化幅度由以下公式计算

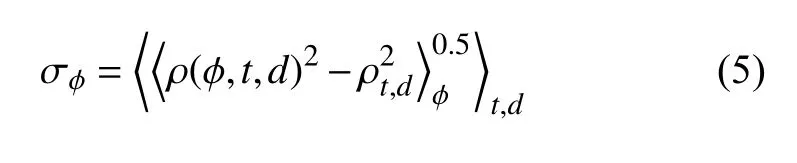
σa可用于衡量不同因素对密度影响的重要性.

2 时空扰动规律

图1(a)～图1(c)依次显示了纬度、地方时和日期对密度影响的基本规律.从图1(a)中可以看出,除75～90 km 范围以外,纬度越低密度越大;75～90 km 高度,极地平均密度最大,低纬度次之,中纬度密度最小.图1(b)显示低于60 km 时,昼夜变化对密度影响较小;高于60 km 时,密度在7:00 附近达极小值,13:00 附近达极大值.从图1(c) 可以看出,低于90 km 时,全球平均密度在 6 月和12 月,即太阳直射南北回归线时达极大值;高于90 km 时,全天南海北密度在 6～7 月达极小值,此时,地球处于远日点附近.为进一步研究太阳辐射对地球大气密度的影响规律,图2(a) 和图2(b) 分别显示了70 km 和100 km 高度,不同纬度,大气密度随日期的变化规律.100 km 高度,同一日期的密度有较好的南北半球对称性,南北半球平均密度均在近日点附近达最大值;70 km 高度,南北半球随日期的变化存在半年的相位差,密度均在自身半球的夏至日达最大值,在自身半球的冬至日达最小值.结合图1(c)说明日地关系对地球大气密度的影响体现在两方面,即太阳直射纬度和日地距离.夏季半球的太阳辐照强度大于冬季半球,近日点全球接收的太阳辐射能量大于远日点.不同高度下南北半球密度以及全球平均密度随日期变化的差异,可能与不同高度下大气环流及能量传输方式有关.

图1 卫星观测的14～108 km (a) 纬度、(b) 地方时和(c) 日期对大气密度的影响规律Fig.1 Variations of atmospheric density with (a) latitude,(b) local time and (c) date observed by satellite at altitudes from 14 to 108 km

图2 高度(a) 70 km 和(b) 100 km,(ϕ,d)平面内的大气密度变化规律Fig.2 Variations of atmospheric density with ϕ and d at altitudes of(a) 70 km and (b)100 km

为定量比较纬度、日期和地方时对密度影响的重要性,图3 显示了纬度、日期和地方时引起的密度扰动幅度随高度的变化.扰动幅度与统计平均获得 ρ(ϕ,t,d) 时选择的 ϕ,t,d区间宽度有关.区间越小,变化幅度计算值越大.当区间小于密度扰动的最小尺度时,计算幅度值趋于收敛.本文使用的区间大小如前文1.2 节所述.从图3 中可以看出在14～108 km范围内,对密度扰动的影响,纬度 >日期 >地方时.地方时引起的密度扰动均方值在40 km 高度以下区域小于1%,较小的密度变化幅度与图1(b) 所示结果一致.高于40 km 时,地方时引起的密度扰动幅度随高度单调增加.纬度和日期引起的扰动幅度在78 km附近达最大值;密度扰动幅度在22 km 和92 km 附近达局部极小值.

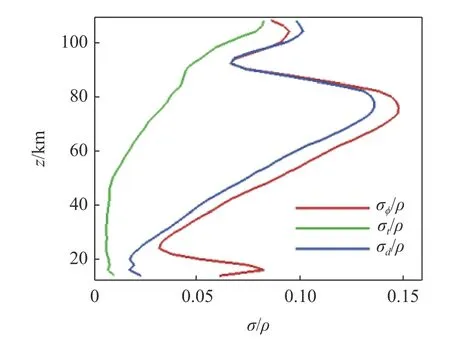
图3 纬度、日期、地方引起的密度扰动幅度随高度的变化规律Fig.3 Profiles of variation amplitudes caused by latitude,local time and date

3 临近空间大气密度时空扰动模型

本节将基于卫星测量数据统计得到的 ρ (z,ϕ,t,d),研究方便易用且精度更高的大气密度模型.一般地,密度可写成平均量和扰动量的形式,即 ρ(z,ϕ,t,d)=ρ(z)[1+Ω(z,ϕ,t,d)].其中,ρ (z) 是高度z处的平均密度,Ω(z,ϕ,d,t)是扰动函数.

为与卫星测量数据区分,将本文大气密度模型描述的密度和扰动函数添加上标“m”以示区分.图4中红色实线显示了卫星测量的平均密度随高度的变化.根据平均密度随高度的变化特征,本文将 ρ (z) 拟合成以下关系式

本文模型以及USSA-76 描述的平均密度相对卫星测量值的偏差如图4 所示.可以看出,卫星测量值相对USSA-76 的密度在22 km 以下偏大,22 km以上偏小,相对偏差在108 km 处达最大值29%;本文模型的平均密度与测量值相对偏差处于(−3.2%,2.9%),说明模型中平均密度表达式可较好地描述测量结果.

图4 卫星测量平均大气密度及其与USSA-76、本文模型的相对偏差Fig.4 Profiles of averaged atmospheric density observed by satellite and its relative deviation from USSA-76 and present model

根据大气密度的变化特征,假设密度扰动函数具有以下形式

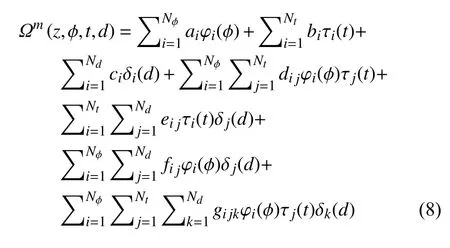
式中,Nϕ,N t,N d是常数;ai,bi,ci,d ij,e ij,fij,gijk均是z的函数,φi(ϕ) , τi(t) , δi(d) 分别是关于纬度、地方时和日期的函数.

以往模型如USSA-76,NRLMSISE–00 模型均是通过建立温度剖面模型,结合静力平衡方程得到密度分布,而本文则直接以密度为物理量建立模型.USSA-76 模型通过平均温度剖面,获得密度平均随高度的变化曲线[13].MSIS 系列模型如MSIS-86,NRLMSISE–00 在平均温度剖面基础上,引入了中间层顶高度、温度、扩散−混合过渡区等随地方时、日期、太阳活动和地磁活动的变化规律,对不同高度下的变化特性缺乏详细的考虑[14-15].从图1 可以看出,大气密度随纬度、日期、地方时的变化幅度及相位均与高度强相关,而本文中的时空扰动模型描述的扰动幅度与相位均是高度的函数,因此时空扰动模型对不同高度段范围内的密度变化规律理应具备更好的描述.

扰动函数 φi(ϕ),τi(t),δi(d) 应满足守恒条件,即

根据图2 和图3 显示的密度变化规律,可假设扰动函数

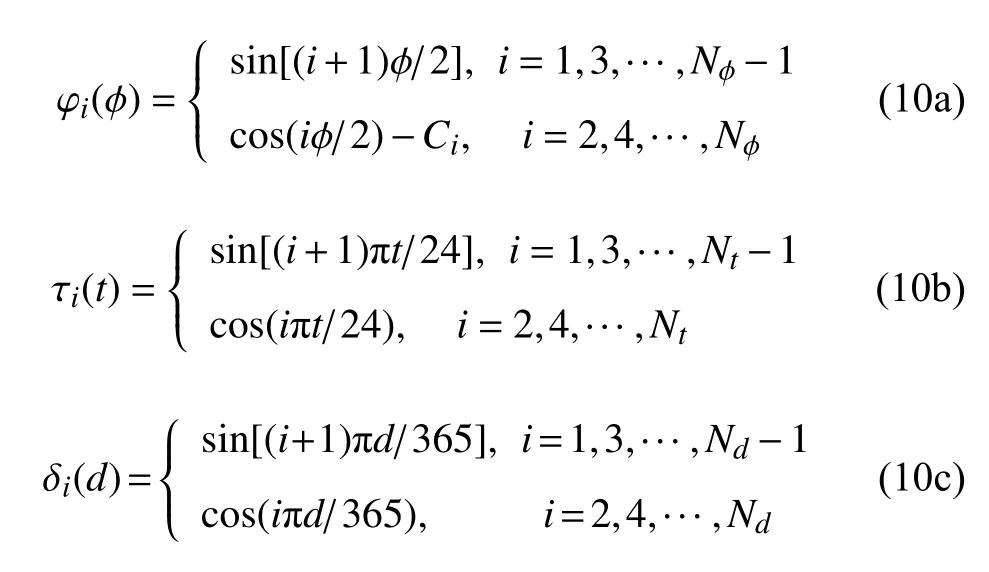
式中,Ci是为了满足式(9a) 的常数,例如C2=π/4 ,C4=1/3.

为体现密度变化的主要特征,本文设Nϕ=4 ,Nt=6,N d=6 ,即着重描述密度随纬度的变化规律,昼夜变化引起的周日、半周日及1/3 周日的变化规律,日期变化引起的周年、半周年及1/3 周年变化的变化规律.进一步,通过数据拟合可得到特定高度的ai,bi,ci,d ij,e ij,fij,g ijk.

图5 显示了卫星测量值的扰动量随高度的变化规律.图6(a)显示了 Ω −Ωm随高度的变化.Ω 与 Ωm的偏差越小,说明模型对密度测量值的还原度越高.Ω−Ωm的值99%处于 (−0.2,0.2).对比图5 中 Ω 为68.3% 和99%的分布范围,可以看出 Ω −Ωm的幅度明显小于 Ω.图6(b)显示了 (ϕ,t,d) 空间内 Ω −Ωm的均方根随高度的变化.在研究的高度范围内,Ω−Ωm的均方根小于0.07.Ω −Ωm的均方根在21 km 和91 km 附近达局部极小值,分别为0.012 和0.043;82 km 左右达局部极大值0.052.

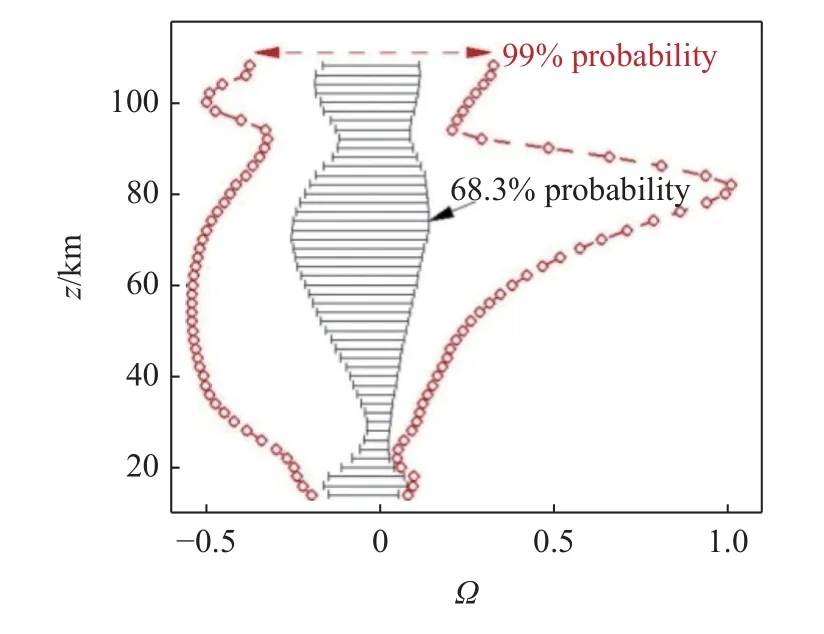
图5 14～108 km 高度下,卫星测量的密度时空扰动项的特征分布范围Fig.5 Range of temporal-spatial fluctuations of density observed by satellite at altitudes of 14～108 km

图6 时空扰动测量值与模型值之差在高度14～108 km 内的变化.(a)均值及特征分布范围和(b)均方根Fig.6 Difference of temporal-spatial fluctuations of density between observed values and modeled values at altitudes of 14-108 km.(a) Mean value and range (b) root of mean square

图7 显示了模型中纬度、日期和地方时引起的密度扰动与高度的关系,对比图1 可以进一步看出,本文模型可反映不同高度下密度时空扰动的主要特性.

图7 本文模型描述的(a) 纬度、(b) 地方时和(c) 日期对大气密度的影响在高度14～108 km 内的变化Fig.7 Variations of atmospheric density with (a) latitude,(b) local time and (c) date calculated by present model at altitudes from 14 to 108 km

为进一步分析对比模型与密度测量结果,图8给出了80,90,100 km 高度,NRLMSISE-00,USSA-76 和时空扰动模型与SABER 观测数据随纬度的分布.从图中可以看出,USSA-76 模型在90,100 km 高度明显高于SABER 测量数据的平均值,与图4 所示结果一致.时空扰动模型描述的密度数值点的分散性弱于测量结果,这是因为时空扰动模型考虑的是大气密度随时空变化规律的平均效果.图8 中显示,时空扰动模型能较好地描述密度的时空分布特征.

图8 (a) 80 km,(b) 90 km,(c) 100 km 高度下,SABER 数据与三种模型预测结果对比.红点: SABER,绿点: NRLMSISE-00 模型,蓝点: 时空扰动模型,黑线: USSA-76 模型Fig.8 Comparison of three atmospheric density models and observed data at altitudes (a) 80,(b) 90,(c) 100 km.Red symbol: SABER,green symbol: NRLMSISE-00,blue symbol: temporal-spatial variation model,black line: USSA-76

4 置信区间

本文模型仅考虑确定性因素即纬度、地方时、日期对密度扰动的影响.实际大气还受到随机性因素如湍流输运、地磁活动、太阳活动的影响.本节将采用文献[38]中的误差带和置信度方法来评估对比3 种典型的大气模型即USSA-76,NRLMSISE-00和时空扰动模型.假设样本总数为N,给定误差带ε,若满足

样本数为M,则置信度

式中,ρm和 ρ 分别是模型预测值和观测值.

表2 给出了密度变化较大的3 个典型高度即80,90,100 km 高度,不同误差带要求下3 种模型对比SABER 数据的置信度.从表中可以看出,本文模型的置信度在不同高度均明显高于USSA-76,NRLMSISE-00 模型.高度 80 km,误差带 ± 30%时,USSA-76,NRLMSISE-00 模型的置信度分别为66.1%,88.6%,而时空模型的置信度可达99.0%.90 km 高度,误差带 ±30%时,USSA-76,NRLMSISE-00 模型的置信度分别为68.3%,76.5%,而本文模型的置信度可达98.7%.100 km 高度,误差带 ±30% 时,USSA-76,NRLMSISE-00 模型的置信度分别为73.0%,75.4%,而时空扰动模型的置信度可达93.2%.

表2 高度80,90,100 km,3 种大气模型,不同误差带要求下,对比SABER 数据的置信度Table 2 Altitudes 80,90,100 km,under different error bands,confidence coefficients of the three atmospheric models compared to SABER data

在不同误差带下,本文模型相比经典模型均有较高的置信度,说明形如式(8)的时空扰动模型能很好地描述大气密度的时空扰动特性.与其他模型相比,时空扰动模型不仅考虑了密度随不同因素的变化规律,还考虑了不同因素之间的相互耦合作用.随着探测技术的发展和数据积累,可进一步优化模型参数,提高模型的预测精度.

5 结论

本文利用卫星测量数据,研究了14～108 km 高度范围的大气密度随纬度、地方时、日期的变化规律.在研究的高度范围内,日期和纬度对密度的影响大于地方时的影响.在40 km 以下,地方时引起的密度扰动平均小于1%,高于40 km 时,地方时引起的密度变化幅度随高度线性递增.纬度和日期引起的密度变化幅度在78 km 附近达最大值.纬度对密度的影响可分为两个区域,即75～90 km 高度区域和其他区域.在75～90 km 高度,极区平均密度最大,中纬度平均密度最低;其他高度,低纬度平均密度最大,极区平均密度最小.日期对密度的影响由太阳直射纬度和日地距离有关,低于90 km 时,由日期引起的直射纬度的变化影响较大,高于90 km 时,由日期引起的日地距离变化影响较大.

根据密度变化规律,本文提出了大气密度的时空扰动模型,考虑了密度随纬度、地方时和日期的变化特征.与以往经验模型相比,时空扰动模型能更好地描述不同高度下密度随纬度、地方时和日期的变化规律.相较USSA-76 和NRLMSISE-00 模型,在相同误差带下,时空扰动模型的置信度明显更高.误差带为 ±30% 时,时空扰动模型在80,90,100 km高度的置信度达99.0%,98.7%,93.2%,说明模型能很好地反映密度的时空变化规律.

本文研究增加了对临近空间大气密度及其时空扰动规律的认识,文中建模方法合理,模型结果对临近空间高超声速飞行器动力设计有参考意义.

致谢

本文使用的TIMED/SABER 数据来自美国TIMED计划数据中心(MDC)科学数据系统 (SDS)中SABER数据发布网页http://saber.gats-inc.com.