多层平行裂隙型多孔介质通道内流体流动传热特性1)
2022-12-18李琪王兆宇胡鹏飞
李琪 王兆宇 胡鹏飞
(东北电力大学能源与动力工程学院,吉林省吉林市 132012)
引言
含裂隙多孔介质是地层常见的地质结构.多孔介质中裂隙的存在直接影响地层内流体的运动阻力及换热程度,研究含裂隙多孔介质内的流动传热现象对石油或天然气开采,地热能利用,核废料处理等有重要意义.
有关全部填充多孔介质通道内的流动和传热研究如下.Nield 等[1]基于Brinkman 模型以及局部热平衡模型,在考虑轴向传导和黏性耗散的条件下,分析了全部填充多孔介质平行板通道内的对流传热特性.Hooman[2]基于Brinkman-Forchheimer 模型,讨论了完全填充多孔介质通道内流体的速度渐进解及数值解.Li 等[3]基于局部热平衡模型,采用有限体积法,研究了上下壁面施加不同热通量时,通道内两相流动和传热的瞬时变化.Al-Farhany 等[4]基于Forchheimer-Brinkman-extended Darcy 模型,对全部填充可变孔隙度的稳态共轭双扩散自然对流和传热进行了数值研究.Dehghan 等[5]基于Brinkman-Darcy 模型以及局部热平衡模型,在考虑速度滑移和温度跃变的前提下,数值研究了全部填充多孔介质通道内的对流−传导−辐射复合传热,得出速度滑移系数变化对努塞尔数的影响要低于温度跃变系数变化对努塞尔数的影响.Celli 等[6]基于局部热非平衡模型,分析了通过全部填充多孔介质通道的强制对流热边界层问题.Vadasz[7]通过局部热非平衡模型,研究了在垂直多孔介质层中两侧壁施加不同热条件情况下的自然对流特点.Alomar 等[8]基于局部热非平衡模型,采用有限体积法对全部填充多孔介质通道内的两相流动及其相变过程进行了数值模拟.Parhizi等[9]基于局部热非平衡模型,且假设毕渥数在通道内是变化的前提下,数值分析了全部填充多孔介质通道中流固两相传热特性.Abbasbandy 等[10]给出了多孔介质采用Brinkman-Forchheimer 求解对流问题时的隐式精确解.Hashemi 等[11]采用Brinkmanextended Darcy 模型结合壁面速度滑移和温度跳跃边界条件,讨论了全部填充多孔介质微形通道内的强化传热特性.
对于两侧或底部填充多孔介质的单裂隙通道内的流动传热研究如下.Lisboa 等[12]基于积分变换法以及Brinkman-Darcy 模型对两侧填充多孔介质中的饱和流动进行了探讨.Torabi 等[13]基于Brinkman-Darcy 模型和局部热非平衡模型,对考虑内热源的两侧填充多孔介质通道内的传热和熵产进行了数值讨论.Li 等[14-15]也基于Brinkman-Darcy 模型和局部热非平衡模型,研究了采用应力跳跃界面条件及不同热界面条件时两侧填充多孔介质通道内的流动换热特性.Ucar 等[16]基于Brinkman-Darcy 模型以及局部热平衡模型,对底部填充的单裂隙多孔介质通道内的强制对流传热进行了数值研究,得出多孔介质厚度对速度分布影响较大,当多孔介质区厚度增加时,自由流体区速度增加,且当文中定义的热导率为1 时,努塞尔数为最大值.Kuznetsov 等[17]也研究了底部填充多孔介质平行板通道内强制对流,讨论了带有界面处滑移速度条件下的流动传热特性.李琪等[18]基于Brinkman-extended Darcy 模型,在考虑界面应力跳跃条件下获得了底部填充多孔介质非对称通道内流体流动特性解析解.之后又基于局部热非平衡模型求解了两侧填充多孔介质通道内温度场及努塞尔数解析解[19].Satyamurty 等[20]得出,恒壁温条件下底部填充多孔介质平行板通道内的换热强度最佳为达西数1.0 × 10−3且空心率0.8 时的情况.
对于中间填充多孔介质的双裂隙多孔介质通道内的流动传热研究如下.Mahmoudi 等[21]基于Brinkman-Darcy 模型以及局部热非平衡模型,分析了壁面施加恒定热流的中间填充多孔介质通道内的强制对流.Yang 等[22]在界面处应用速度滑移条件以及不同热边界条件,讨论了局部热非平衡模型下中间填充多孔介质内的流动传热特性.得出了不同种条件下两相温度的解析表达式以及努塞尔数.此外,还讨论了局部热平衡模型的有效性.Cekmer 等[23]理论研究了在平行通道中间插有多孔介质平板内的对流传热特性.讨论了不同达西数、热导率和多孔介质填充厚度下的速度和温度分布.Mahmoudi 等[24]采用Darcy-Brinkman-Forchheimer 模型以及局部热非平衡模型,对中间填充多孔介质通道内的流体展开了传热传质研究,确定了多孔介质强化传热的最佳厚度.Teamah 等[25]基于Darcy-Brinkman-Forchheimer 模型以及局部热平衡模型,数值研究了中心处插入圆柱多孔介质材料及圆环多孔介质材料管道内的流动传热问题.
此外,Choo 等[26]将多孔介质分为两个孔隙区域分别为大孔隙和微孔,并给出稳定有限元法来耦合双重孔隙介质中的固相形变和流体扩散.Torabi 等[27]通过有限体积法,从孔隙尺度对流体绕流多孔介质方形截面和圆形截面内的流动传热进行了讨论.Kundu 等[28]通过改变多孔介质的颗粒直径以及多孔介质的渗透率等,对单相流体流过不同类型多孔介质时的流动状态进行了实验研究及数值模拟.Suzuki 等[29]应用相互作用连续法讨论了裂隙与基质之间的相互作用.Berrone 等[30]基于离散裂隙和基质模型,在多孔介质中的流动符合达西定律的条件下,提出了一种可以在裂隙型多孔介质中进行流动模拟的方法.Baragh 等[31]实验研究了通道内不同排列方式多孔介质的对流换热.Kačur 等[32]数值研究了非饱和−饱和多孔介质内的热质传递特性.Morales 等[33]对饱和多孔介质及狭窄自由通道界面处的流体交换和应力平衡的极限问题进行了研究.孟旭辉等[34]基于格子波尔兹曼数值方法讨论了流体流经多孔介质通道时流相与固相间的动量交换过程并提出一种高效的动量交换法来计算流固作用力.侯晓萍等[35]采用复合单元法建立了模拟裂隙多孔介质变饱和流动的数值模型,讨论了裂隙与多孔介质之间的相互作用.并在此基础上获得了局部热非平衡条件下的温度场.
综上所述,含裂隙多孔介质内的流动传热现象一直受到研究者的广泛关注.对于离散无规则多裂隙多孔介质内的流动传热复杂且较多是数值模拟研究并忽略界面效应,无规则裂隙较难总结其规律.而采用解析解法并考虑界面条件所研究的规则裂隙,几何模型多数为中间填充多孔介质的两层平行裂隙型多孔介质通道及底部或两侧填充多孔介质的单层平行裂隙型多孔介质通道,鲜有采用解析解的方法研究多层平行裂隙型多孔介质通道内即填充多孔介质通道内含有多层数量的平行裂隙层情况下流体的流动传热特性.本文基于局部热平衡模型以及Brinkman-extended Darcy 模型,并结合界面应力跳跃条件,对多层规则平行裂隙型多孔介质通道内的流动传热特性进行理论分析.首先以两侧填充多孔介质的单层平行裂隙为基础,用来验证解析结果的正确性,之后扩展成多平行裂隙层通道结构,并对不同裂隙层数下通道内各区域的速度场、温度场以及努塞尔数进行理论求解,最终获得包括裂隙层数、裂隙总高度等参数对通道内对流换热的影响规律,以了解含裂隙多孔介质地质结构中裂隙的存在对地层内流体速度、运动阻力及换热程度的影响.
1 物理数学模型
如图1 所示,本文所研究的模型是在填充多孔介质的平行板通道内添加一层或多层平行裂隙,将其变为多界面平行裂隙型多孔介质通道.通道内的多孔介质层都具有相同属性,包括渗透率、孔隙率、热导率等.图1(a)所示为中间单层平行裂隙多孔介质通道,此时通道内裂隙层数n=1,设通道总高度为2h0,裂隙层总高度为2hf,则空心率S=2hf/(2h0).进一步地,维持单裂隙总高度不变,将其拆分为n个相同高度裂隙层,并将n个裂隙层均匀插入到通道内,即如图1(b)~图1(e)所示通道内裂隙层数n=2,3,4,5.此外,如图1 所示,为了区分不同位置裂隙层及多孔介质层表达式,取j为自由流体区位置序号,取k为多孔介质区位置序号,其中,当n=1 时,j=k=1;当n=2 时,j=1,k=1,2;当n=3 时,j=k=1,2;当n=4 时,j=1,2,k=1,2,3;当n=5 时,j=k=1,2,3.假设Sn(n=1,2,3,4,5)为通道中心线到各层裂隙界面的高度,则S与Sn的关系如表1 所示.假设流经此通道的流体为压力驱动的不可压缩层流且充分发展,通道上、下平板均受非渗透性固体壁面边界限制且均施加以均匀的热流密度qw(W·m−2),忽略多孔介质内流固两相温差,不考虑自然对流和辐射换热.

表1 空心率S 与Sn 的关系Table 1 The relationship between hollow ratio S and Sn
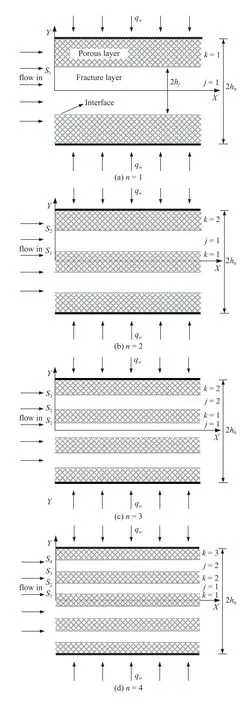

图1 多层平行裂隙型多孔介质通道结构Fig.1 Porous channel structure with multilayer parallel fractures
假定平行通道内流体运动状态为水平压力梯度dp/dx驱动的充分发展层流状态,则多孔介质层和裂隙层运动方程[14,19]分别为

式中,μeff为多孔介质层的有效动力黏度(kg·m−1·s−1),μf为流体的动力黏度(kg·m−1·s−1),up为多孔层的流体速度(m·s−1),其中下标“p”表示多孔介质层,uf为裂隙层的流体速度(m·s−1),其中下标“f”表示裂隙层,k为多孔介质渗透率(m2),多孔介质流体运动方程采用Brinkman-extended Darcy 模型如式1(a)所示.壁面处边界条件为

多孔介质层与裂隙层交界面处引入应力跳跃界面条件,如下所示[36-37]
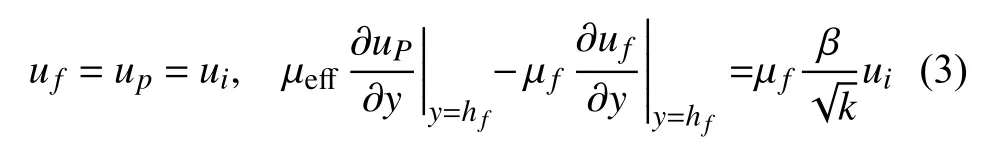
式中,β为界面应力跃变系数,ui为流体在界面处的流速(m·s−1),但需注意多裂隙时不同界面处的界面速度并不相同.
中心线处流体运动边界条件

多孔介质层和裂隙层内能量方程分别为[14,19]

壁面处热边界条件为

多孔介质层与裂隙层交界处的热边界条件为

中心线处热边界条件

式中,kf为通道内自由流体区内流体的导热系数(W·m−1·K−1),kef和kes分别为多孔介质层内流体有效导热系数和固相有效导热系数(W·m−1·K−1),tw为壁面处的温度(K),ti为界面处的温度(K).
2 解析解
2.1 速度分布
为简化计算,研究一般性规律,引入以下无量纲变量

其中,本文将多孔介质的有效动力黏度μeff取μeff=μf/ε,则M=1/ε[18],把式(9)的无量纲化参数代入式(1)~式(4),得到多平行裂隙各区域速度场分布
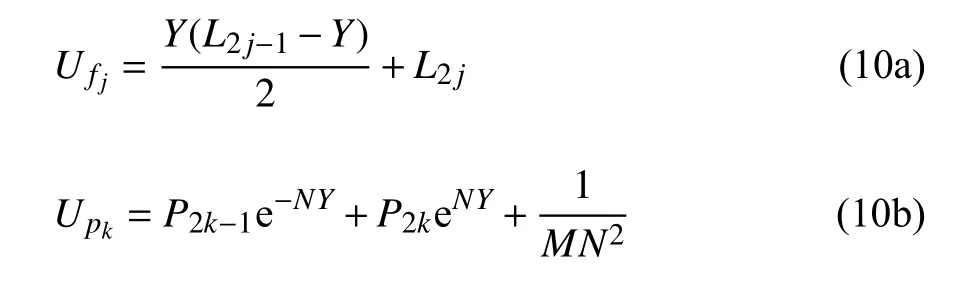
其中,附录中附表1 为裂隙层速度场系数Lj表达式,附表2 为多孔介质层速度场系数Pk表达式,且各速度分布系数中包含的各界面速度根据界面应力跃变条件即式(3)获得.
2.2 温度分布
将式(9)的无量纲化参数代入式(5)~式(8)得到多层平行裂隙型多孔介质通道内各区域温度场分布

单裂隙(n=1)

双裂隙(n=2)
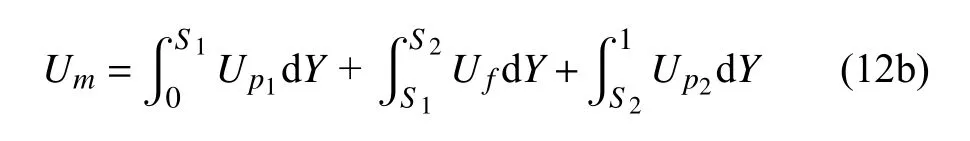
三裂隙(n=3)
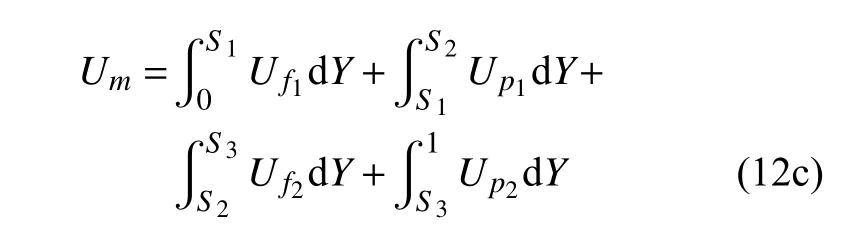
四裂隙(n=4)

五裂隙(n=5)

2.3 f,Re 以及Nu 表达式
部分填充多孔介质通道摩擦系数的计算公式为[21]

式(13)也反映了通道内流体压降大小.
部分填充多孔介质通道内努塞尔数的计算公式为[38]

其中hx是对流传热系数

将式(9)代入式(15)和式(16),可得Nu的无量纲表达形式为
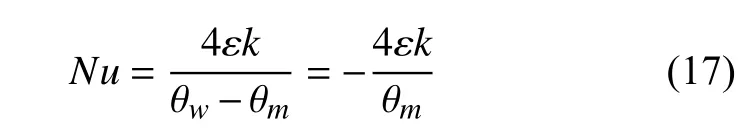
其中θm为通道平均温度.对于不同裂隙而言,其表达式如下
单裂隙(n=1)

双裂隙(n=2)

三裂隙(n=3)
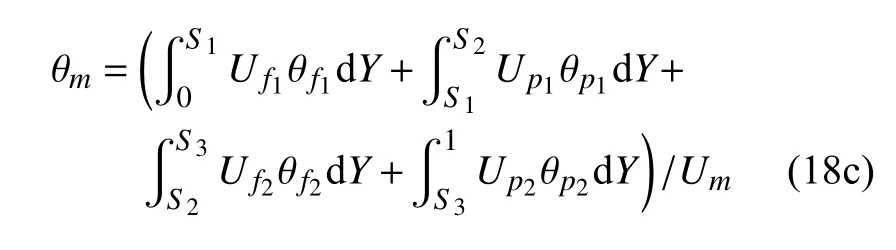
四裂隙(n=4)
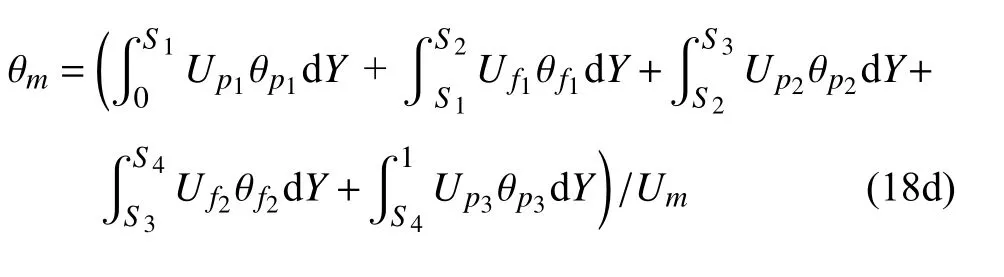
五裂隙(n=5)
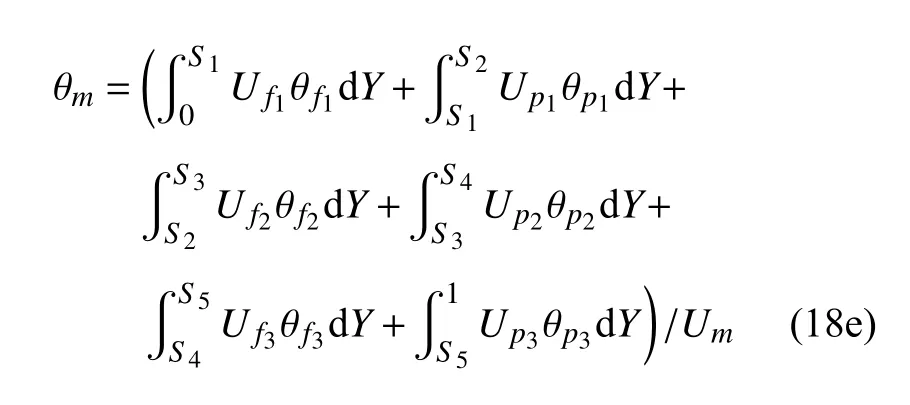
将所得流场精确解式(10)、温度场精确解式(11)以及附表1~附表4 代入式(12)~式(17),可以得到不同裂隙数下摩擦系数和努塞尔数解析解.由于各裂隙层数下所得f,Re和Nu解析解太复杂,故不在论文中展示.

附表 1 裂隙层速度场系数Lj 表达式Table 1 Coefficient expressions Lj of velocity field in fracture layers
3 结果与讨论
3.1 结果验证
将本文的计算结果与文献[14]在相同工况下计算结果进行对比,文献[14]所研究的是通道两侧填充多孔介质即中间为单裂隙的部分填充多孔介质通道.发现在Da=1.0 × 10−3,ε=0.9,β=0,K=10 时,本文计算的解析解结果与文献[14]得到的解析解结果一致,计算结果对比如图2 所示,证明了本文计算结果的正确性.

图2 本文计算结果与文献[14]结果比较Fig.2 Comparison of the calculation results of this paper with the results of Ref.[14]
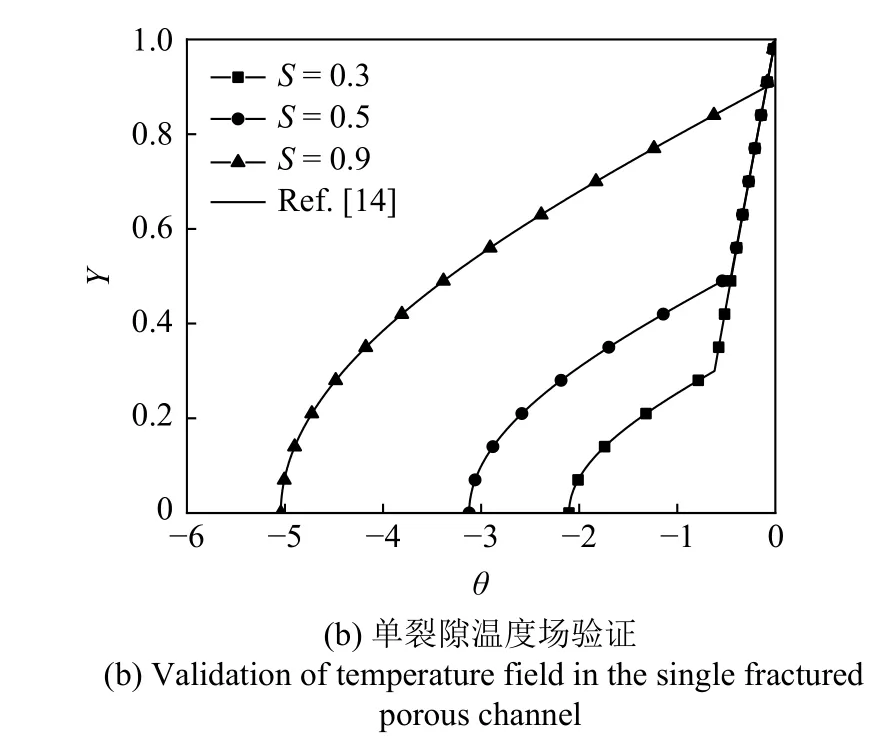
图2 本文计算结果与文献[14]结果比较(续)Fig.2 Comparison of the calculation results of this paper with the results of Ref.[14] (continued)
3.2 不同参数对速度场、压降的影响
图3 所示为ε=0.9,β=0,S=0.5 时,不同裂隙层数n、达西数Da下,通道各区域速度场分布.由图可以看出,当Da=1.0 × 10−3时,随着裂隙层数n的增加,裂隙层内流体的最大速度在逐渐减小,而多孔介质层内的流体速度逐渐增大,说明当插入多孔介质层数越多时,整个通道内流体速度变化范围在逐渐减小,会使流速变化在通道内更加均匀.当Da=1.0 × 10−5时,如图3(b) 所示,由于达西数Da较小,意味着多孔介质渗透性较弱,各裂隙层内和各个多孔介质层内的速度大小范围变化都不大.流体在各个多孔介质层内的速度非常小,且出现不随Y变化的速度称为达西速度UDarcy,此达西速度因裂隙层数的变化而变化,不受各裂隙层下多孔介质层位置变化的影响,即n=1,2,3,4,5 时,裂隙层数一定情况下各多孔介质层内的达西速度相同,分别为UDarcy=2.354 48 × 10−4,9.233 98 × 10−4,2.04 × 10−3,3.55 × 10−3,5.44 × 10−3,发现随着裂隙层数的增加,多孔介质层内的达西速度是逐渐增大的.此时,由于多孔介质层内渗透率的降低且接近不渗透壁面,各裂隙层内流体最大速度基本相同.

图3 裂隙层数对速度场的影响Fig.3 Effect of the number of fracture layers on velocity distribution
图4 所示为当S=0.5,Da=1.0 × 10−3时,不同裂隙层数下,孔隙率ɛ对速度分布的影响.由图可以看出,Da=1.0 × 10−3确定情况下,孔隙率越小交界处的速度变化越剧烈,在裂隙层与多孔介质层交界处会出现陡峭的速度梯度,如ɛ=0.1 时,这是因为流体流过通道时内部的孔隙率突然变化剧烈引起的,而孔隙率越大多孔介质越接近自由流体区,其内部速度分布就越接近抛物线,如ε=0.9 时.在各裂隙层数下,改变孔隙率对裂隙区内及近壁面处多孔介质区内的流体速度分布影响较小,而孔隙率对非近壁面多孔介质区内的流体速度分布的影响则会随裂隙层数n的增加而变化明显,其内的流体最小速度会随裂隙层数n的增大或孔隙率的减小而增大.
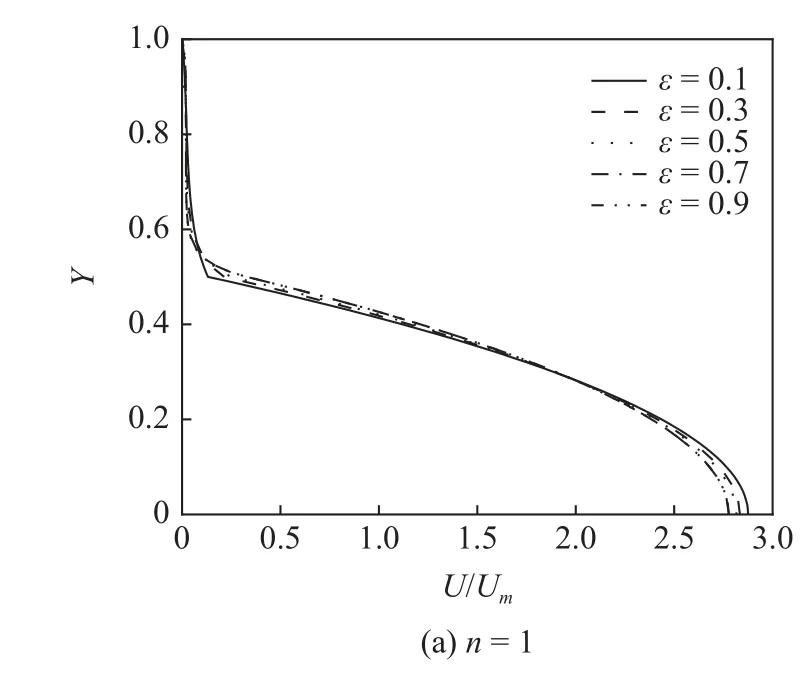
图4 孔隙率对速度分布的影响Fig.4 Effect of porosity on velocity distribution
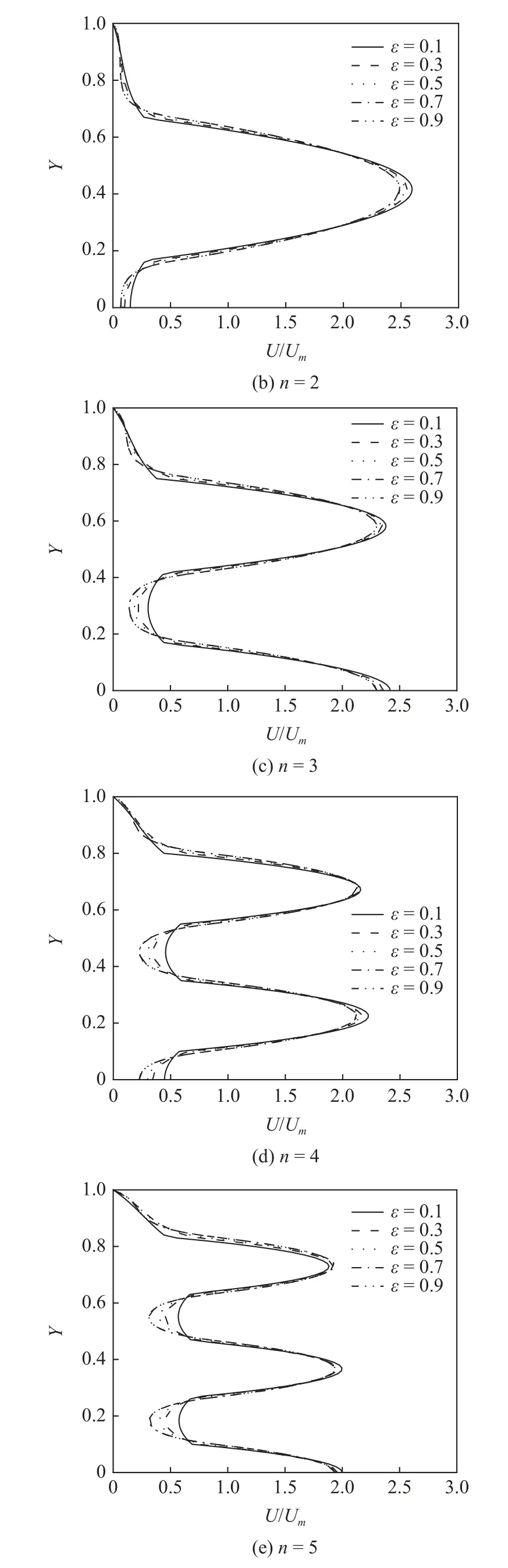
图4 孔隙率对速度分布的影响(续)Fig.4 Effect of porosity on velocity distribution (continued)
图5 所示为ε=0.9,β=0,Da=1.0 × 10−3时,不同裂隙层数n,空心率S对速度分布的影响.由图5(a)可以看出,在各空心率S下即总裂隙高度不变时,当裂隙层数增加时,裂隙层内的流体最大速度会减小且减小的程度逐渐降低,而多孔介质区内流体的速度有所增加,即通道内的流速分布变化范围变小,使流速变化在通道内更加均匀.相同的现象在图5(b)~图5(d)也可以看出,且都与图3(a)的结论一致,所不同的是图5(a)中多孔介质区内的速度近似均匀,而由于拆分裂隙层数n的增多或总裂隙高度S的减小都会使多孔介质区域内速度均匀性下降.此外,对比图5(a)~图5(d)S=0.1,0.3,0.7,0.9 及图3(a)S=0.5 可以明显看出,当n=1 单裂隙时,减小空心率S会增大裂隙层内流体最大速度,而使多孔介质层内的流体速度更均匀,这是因为减小S意味着多孔介质填充增多,大部分流体会流至无阻的裂隙区而剩余流体则会在多孔介质区内受固相阻碍而使流体速度更加混合均匀;当n>1 时,在确定了多层裂隙层数下,减小空心率也会使多孔介质层内的速度更加均匀,而裂隙层内的流体最大速度则会先增大后减小.造成裂隙层内流体最大速度随S降低先增大的原因与n=1 时的情况相同,而之后裂隙层内的最大速度又减小则是因为当空心率降低到一定程度时,由于将单裂隙拆分成多裂隙,多层裂隙通道内各裂隙层的高度变为多个更窄通道的裂隙层,致使裂隙层内不能再容纳较多流体而使部分流体流向多孔介质层内,因此又导致裂隙层的最大速度后续的减小.另外还可以看出,在空心率较大时,裂隙层数对通道内最大速度的影响程度变小,如在S=0.9 时,这是因为在空心率较大时,多孔介质层的总高度较低,以至于分层后由于高度较小所以对各裂隙层内的最大速度影响也不大,使通道内速度变化范围相对较小较集中.总之,多裂隙层内各区域的速度分布受空心率和裂隙层数的共同影响.

图5 空心率对速度分布的影响Fig.5 Influence of hollow ratio on velocity distribution
图6 所示为ε=0.9,β=0 时,不同裂隙层n,达西数Da下压降随空心率的变化.由图6(a)中Da=1.0 × 10−3可以看出裂隙层数一定时,压降均随空心率的增加而单调递减,且可以看出压降在空心率较小时比较敏感,特别在S=0 时即流体通过完全填充多孔介质通道时的压降远高于部分填充多孔介质通道.相比于图6(a),图6(b)为较小Da情况,显然,Da=1.0 × 10−5情况下的压降要高于Da=1.0 × 10−3情况,在S=0 时高出了两个数量级,随后随着S→1 又趋于一致,均为f · Re→24,与无多孔介质填充通道内的结果相同.在小Da下,空心率较小时的压降随S变化更为敏感.由图6(a)和图6(b)还可以看出,裂隙层数的增加会减弱空心率对压降的影响,增加裂隙层数会使相同空心率下通道的压降升高,且升高程度会随裂隙层数的增加而降低.

图6 不同裂隙层数和达西数下压降随空心率变化Fig.6 Variation of pressure drop with hollow ratio under different fracture layer numbers and Darcy numbers
3.3 不同参数对温度场影响
图7 所示为Da=1.0 × 10−3,β=0,ε=0.9,K=10 时,不同空心率下,裂隙层数n对温度分布的影响.由图7 看出,S一定时,单裂隙情况下的温度分布与多裂隙情况差别较大,且单裂隙通道中心处的最低温度要低于多裂隙情形.图7(a)中S=0.1 时,多裂隙通道内温度分布呈现“阶梯式”.近壁面处多孔介质层内温度变化近似线性,发现近壁面处多孔介质区内温度变化由于受恒热流边界的影响其变化范围较其他位置处多孔介质层内的温度变化范围要大,且多孔介质层的位置越靠近通道中心,其内流体的温度变化就会越小越均匀.裂隙层虽然较窄,但其内的温度变化率要明显大于多孔介质层内的温度变化率.在空心率保持不变的前提下,增加裂隙层数会导致多孔介质层增加,由于多孔介质层具有良好的换热特性,其均匀插入通道会使通道内的温度分布更加均匀.随着S的增加,如图7(b)~图7(e),由于裂隙高度的增加,多孔介质高度的减少,整个通道内的“阶梯式”温度分布方式逐渐减弱,裂隙层内的温度变化范围随S增大而增大,多裂隙情况下的温度分布曲线随S的增大而逐渐趋于一致,特别是S=0.9 的情况下,多裂隙层下的温度分布曲线几乎重合.


图7 在Da=1.0 × 10−3,K=10 时,不同空心率下裂隙层数对温度分布的影响Fig.7 Influence of the number of fracture layers on the temperature distribution under different hollow ratios at Da=1.0 × 10−3,K=10
图8 给出的是S=0.5,ε=0.9,β=0,Da=1.0 ×10−3时,不同热导率之比即多孔介质固相有效热导率与流相有效热导率之比K下,裂隙层数对多层平行裂隙型多孔介质通道内流体温度分布的影响.由图8可以看出,在K较小时(K=0.1),没有出现“阶梯式”温度分布,裂隙层与多孔介质层以及界面处温度曲线连接光滑,界面位置不明显,整个通道沿Y方向流体温度变化很小,且在n>1 时不同裂隙层数下各区域流体温度分布均近似相同,所以此时可以忽略裂隙层数对温度的影响.当K=1 时,在多裂隙情况下可以看出界面位置,裂隙层与多孔介质层内的温度曲线特征开始变的不同,“阶梯式”温度分布出现但不明显,整个通道沿Y方向流体温度变化也较小.当热导率K继续增大时(K=10,30),可以看出裂隙层与多孔介质层内的温度曲线开始变的明显不同,多孔介质层内温度变化较小,裂隙层内温度变化较大,“阶梯式”温度分布明显.因此,增大K使裂隙层数对通道内温度的影响增大,只是随着裂隙层数的不断增加,裂隙层数对温度的影响会减弱,整个通道沿Y方向温度变化随K的增加而增大.

图8 不同热导率之比时,裂隙层数对温度分布的影响Fig.8 Influence of the number of fracture layers on the temperature distribution under different thermal conductivity ratios
3.4 不同参数对Nu 的影响
图9 所示为ε=0.9,β=0,S=0.5 时,不同裂隙层数和Da下,Nu与热导率之比K的关系.由图9(a)可以看出Da=1.0 × 10−3时,裂隙层数n一定的情况下,当K较小时,Nu几乎不随K的变化而变化,持续增大K时,Nu会随K的增加而明显增大,而当K增大到一定程度时,K对Nu的影响则又保持平缓,继续增大K则对Nu的影响很小.即在1

图9 Nusselt 数与热导率之间的关系Fig.9 Relationship between the Nusselt number and the thermal conductivity ratio
上图仅是给出了S=0.5 时不同裂隙层数下的Nu随K的变化.为了进一步明确其余空心率下的Nu变化规律,给出了图10.图10 所示为ε=0.9,β=0,Da=1.0 × 10−3时,不同裂隙层数n,不同热导率之比K下Nu与空心率S的关系.由图可以看出,随着K的增加,单裂隙和多裂隙通道的换热效果都增强.对于图10(a),在n=1 单裂隙时,Nu随着S先减小后增加,且在S=0.2 左右存在临界空心率使得Nu最小;当n>1 多裂隙情况时,Nu随着S先减小后增大再减小,但Nu整体变化范围不大,且在S=0.88 附近出现一个交点使得不同裂隙层数下Nu不变.因此,单层裂隙下Nu对S的变化相较于多层裂隙下的情况更加敏感,变化范围更大,且出现最小Nu使通道换热效果最弱,而多裂隙通道内裂隙层数及空心率的变化对Nu的影响均较小.

图10 Nusselt 数与空心率的关系Fig.10 Relationship between the Nusselt number and the hollow rate
图10(b)中K=1 时单裂隙情况下Nu随S变化趋势与K=0.1 时相同,都是先减小后增加,只是后续增加程度不明显,而多裂隙时Nu随S增加而逐渐减小,与K=0.1 随S变化不大的情况不同,空心率S的变化对Nu作用明显,而裂隙层数对Nu的影响仍较小.当继续增加K时,如图10(c)和图10(d)可以看出,无论单裂隙还是多裂隙通道内,其Nu随着S增大均单调递减,且在S较小(S<0.2)时下降越陡峭,即Nu的变化在空心率较小时更为敏感,相反在空心率增大时,Nu受S的变化影响相对较小,这种现象在较大K下更为明显.此外,由图10 还可以看出K一定时,多裂隙与单裂隙下的Nu曲线有所区别,但不同多裂隙下的Nu随S的变化曲线却相差不大,特别是较大K时多裂隙下的Nu随S的变化曲线几乎重合,即n>1 时多裂隙情况下,通道内插入不同裂隙层数时的传热强度相差不大,裂隙层数的增加对Nu随S变化的影响很小.此外,当K=0.1 和1 时,多裂隙层的传热效果要优于单裂隙情况,而当K=10 和30 时可以明显看出在S=0.1 附近多层裂隙之间存在Nu相同的交点,且当K继续增加时,交点会向S较大的方向移动,即在热导率之比较大时,存在某一临界S使得在该空心率下各裂隙层下的Nu(包括单裂隙情况)相同,而在此临界S值之前,单裂隙的换热效果要好于多裂隙情况,在此临界S之后,则多裂隙下的通道换热效果要优于单裂隙情况.
4 结论
本文采用局部热平衡法对多层平行裂隙型多孔介质通道内流体流动换热问题进行研究.获得了考虑裂隙层与多孔介质层界面处应力跳跃情况下,不同平行裂隙层数下多孔介质填充通道内的速度场、温度场、摩擦系数(压降)及努塞尔数解析解.并进一步分析了达西数Da、热导率之比K、裂隙层数n、空心率S等对各层域的速度场、温度分布及换热强度的影响,得到以下结论.
(1)Da较小时,多孔介质层内渗透率接近不渗透壁面,各裂隙层内流体最大速度基本相同,而多孔介质层内会出现不随Y变化的达西速度,且此达西速度会随裂隙层数的增加而增大,但却不受各裂隙层下多孔介质层位置变化的影响.Da较大时,随裂隙层数n的增加,裂隙层内流体最大速度逐渐减小,而多孔介质层内流体速度逐渐增大,说明当插入多孔介质层数越多时,整个通道内流体速度变化范围越小,会使通道内流速分布更加均匀.
(2)压降在低空心率下更为敏感.当空心率S一定时,增加裂隙层数会使通道内压降升高,但升高程度会随裂隙层数的增加而降低,另外裂隙层数的增加会减弱空心率对压降的影响.
(3)单裂隙通道内的温度分布与多裂隙通道内温度分布差别较大,且单裂隙通道中心处的最低温度要低于多裂隙情形,但无论是单裂隙还是多裂隙通道其整个通道沿Y方向温度变化都随K的增大或S的增大而增大.增大K或减小S会使多裂隙通道内出现“阶梯式”温度分布;相反地,减小K或增大S会减弱“阶梯式”温度分布,且多裂隙情况下的温度分布曲线会在较小K或较大S时趋于一致,此时可以忽略裂隙层数对温度分布的影响.
(4)多裂隙与单裂隙下的Nu随S的变化曲线有所区别,但多裂隙情况下,通道内插入不同裂隙层数时的传热强度却相差不大.当K较小时(K=0.1,1) 多裂隙层下通道内的传热效果要优于单裂隙情况,且单裂隙会存在临界S使换热效果最弱;而当K较大时(K=10,30),存在临界S值使各裂隙层数通道内的换热效果均相同,仅在此临界S值之后,多裂隙层通道内的传热效果要优于单裂隙情况,Nu值对较小S更为敏感.
附录



