高超声速高焓边界层稳定性与转捩研究进展1)

陈贤亮 符松

(清华大学航天航空学院,北京 100084)

引言

边界层由层流向湍流的转捩问题在空气动力学基础理论中占有重要地位[1].随着高速、尤其是高超声速飞行器的发展,转捩问题对工程应用的重要性也逐渐体现,甚至成为制约飞行器发展的瓶颈问题[2-4].具体来说,流动转捩对飞行器的气动力和气动热均有重要影响,湍流态时边界层的壁面摩阻与热流可达到层流态时的四倍以上[5],因此对转捩的精确预测与有效控制对飞行减阻和热防护结构设计有决定性影响.然而转捩问题具有高度的复杂性,其以非线性为突出特征并且对众多因素(来流条件、边界条件、壁面几何、气体特性等)敏感[6].正因为其重要性和复杂性,国际上高度重视边界层转捩研究,美国国防科学委员会将边界层转捩问题列为高超声速飞行器设计领域与超燃冲压发动机技术并列的最具挑战性的基础科学难题[7].

进一步地,随着飞行马赫数的不断提高与空域的不断拓展,飞行器的来流会同时具有高马赫数、高焓与高雷诺数的特征(见图1,空速域范围大致为50 km 以下和10 马赫以上),这使得高超声速高焓流动转捩成为新兴的重要科学问题.这里的高焓流动与一般的低焓流动有重要不同,在于来流极高的焓值导致强激波后与边界层内达到数千甚至上万度的高温.高温下空气发生多种热和化学过程,导致了传统的量热完全气体(calorically perfect gas,CPG)假设失效,并甚至出现烧蚀、辐射等一系列复杂物理过程.这些效应被称为高温气体效应1传统上也被称为“真实气体效应(real-gas effects)”,但该名词易与“真实气体”一词混淆,后者是指需要考虑分子间作用力的气体(如范德华方程),而高超声速高焓流动中一般不需考虑气体的分子间作用力.(high-tempera-ture effects)[8].目前,对高超声速高焓流动的研究已成为具有鲜明学科特色和重大需求背景的空气动力学的前沿学科[9-10],而其中的流动转捩问题尤其具有多学科交叉耦合的特征,涉及湍流、物理化学、电磁学等不同学科[11].但目前边界层流动转捩与高温气体效应的耦合作用机理尚不明晰,开展高超声速高焓边界层流动失稳与转捩研究是对转捩基础理论的重要补充,同时也对高速飞行器设计有重要的指导意义.

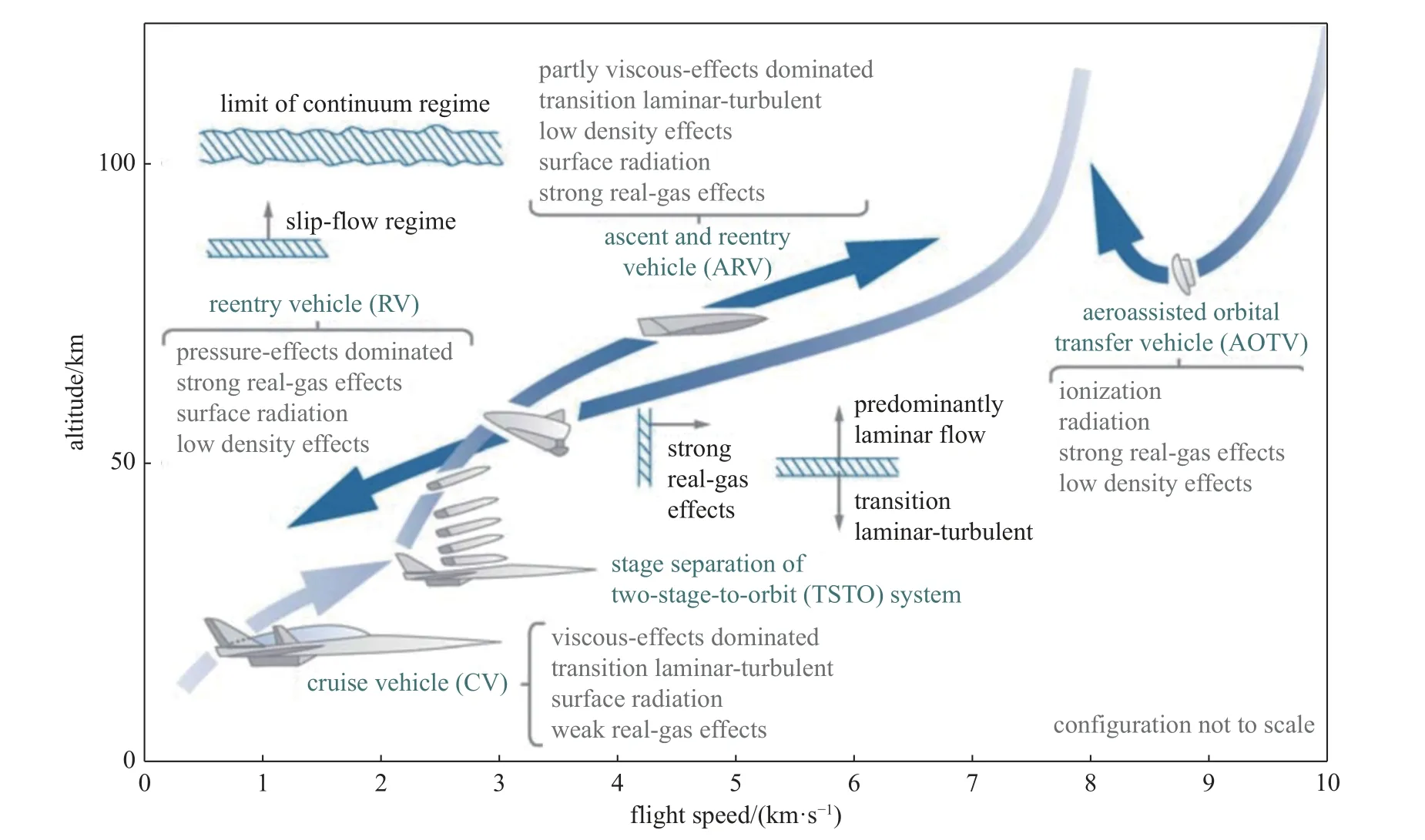
图1 各种飞行器的典型轨迹以及需要考虑的物理问题[2]Fig.1 Typical vehicle trajectories and the physics concerned with [2]

众所周知,转捩是从层流失稳开始的,并涉及感受性、模态增长、非模态增长、非线性作用以至breakdown 等多个过程[12-15].典型飞行器外形的不同流动区域内存在的不稳定性主要有五种: 前缘不稳定性(驻点线模态)[16-17]、流向不稳定性(第一模态和Mack 模态等)[18]、离心不稳定性(主要是Görtler模态)[19-20]、横流不稳定性(横流模态)[21-22]和剪切层不稳定性(多由粗糙单元、台阶等结构引起)[23-24].流向和离心不稳定性一般主导准二维边界层转捩,如小攻角来流的板和锥边界层,而前缘和横流不稳定性多主导三维边界层转捩.目前研究转捩的数值方法主要有三大类,第一类是流动稳定性分析方法,基于层流求解扰动方程,常用的有线性稳定性理论(linear stability theory,LST)[25]、抛物化扰动方程(parabolized stability equations,PSE)[26]、二次失稳理论(secondary instability theory,SIT)[27]、全局稳定性理论[28]等,由此可利用eN方法等进行转捩预测[29-30].第二类是转捩模式理论,通过对转捩过程建模在NS 方程中加入模式方程进行计算,典型代表有k-ω-γ三方程模式[31]、γ-Reθ四方程模式[32]、kL-k-ω三方程模式[33],以及与混合方法结合的RANS-LES-Tr 模式[34]等.第三类是直接数值模拟(direct numerical simulation,DNS)方法[35],即直接求解非定常NS 方程,所需引入的假设最少,而计算代价也最大.将这三种方法以及实验手段有机结合,则既可以研究转捩机理,也可以进行转捩建模,进而实现对飞行器的转捩预测.

已有较多的综述文献介绍了高超声速边界层转捩的研究进展[13,36-40],本文重点介绍高超声速高焓边界层失稳与转捩中出现的新物理与新现象.按照转捩涉及的物理过程划分,目前对高焓边界层层流计算和模态稳定性的研究较多,将在第1 和第2 节中做分别介绍,而针对其他阶段的研究相对较少,相关研究进展见第3 节.第4 节对全文进行总结,并对后续研究提出展望.

1 高温气体物理模型与流场计算

本节首先介绍高温气体物理模型,然后介绍目前针对高焓边界层的相关数值计算与实验手段.

1.1 高温气体效应

一般认为当飞行空域在平流层(高度10～50 km)内时,连续介质模型和NS 方程都是有效的[11].当来流为亚声速或超声速时,流动温度变化一般较小,空气组分不会发生化学反应,分子内能组成也仅为平动能和转动能(后者在50 K 以上时即被完全激发),空气满足量热完全气体假设.随着来流马赫数的不断升高,量热完全气体模型预估的激波后和边界层内的温度都以近马赫数平方的量级快速增长,例如在10 和15 马赫时正激波后温度已达到波前的约20 和45 倍.如此高温下空气组分会经历如图2所示的多种热力学和化学过程.这些热化学过程使得量热完全气体假设失效,并给流动带来重要影响,主要体现在以下几个方面[41-42]:

图2 标准大气压下平衡态空气发生不同热化学过程的温度范围[8,41,43]Fig.2 Temperature ranges of typical thermochemical processes under standard atmosphere [8,41,43]

(1) 分子振动能和电子能的激发,以及化学分解和电离反应都会大幅降低流场温度,进而减小激波层和边界层的厚度.这些效应会影响局部气动力、气动热以及边界层转捩过程,最终影响飞行器的整体气动特性.

(2) 近壁面的高温气体,尤其是氧原子会与壁面材料反应引起烧蚀.烧蚀一方面引起壁面质量射流,另一方面因为质量损失改变壁面形状,形成类似粗糙单元的结构.这些效应尤其影响壁面热流.

(3) 电离反应使得流动介质中存在离子和电子,因而需要考虑电磁效应以及等离子体层的影响.

1.2 热化学平衡与非平衡

为描述高温气体的性质,学者们最先建立的是热化学平衡态(thermochemical equilibrium,TCE)模型,即认为分子的内能分量和化学反应的各组分均符合统计热力学的平衡态分布[8],此时气体状态方程写为

其中p,ρ,T分别为压力、密度和温度,可见压力仍由当地密度和温度唯一确定,只是无法给出统一的解析关系式.将式(1)加入NS 方程后即可使方程封闭,继而求解出处于热化学平衡态的高焓流场.为方便应用,学者们给出了一系列描述平衡态空气热力学和输运性质的拟合式[44-46].图3 给出了正激波后平衡态空气的温度随波前速度的变化,当来流速度超过2 km/s(6～ 7 马赫)时平衡态空气的结果开始偏离量热完全气体,当来流速度为6 km/s (19～ 20 马赫)时两者温差已达到一万度.此外,高度越高则热化学过程的影响越大,因为来流密度和压力的降低促进了化学反应的发生.

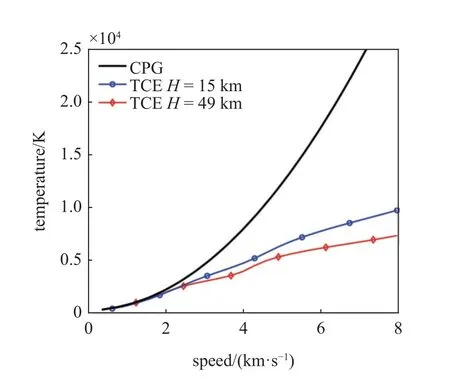
图3 不同高度H 处正激波后温度随波前速度的变化[47]Fig.3 Temperature behind a normal shock with varying pre-shock velocity and altitude [47]

实际上,当热化学过程被引入到流动中时,还需要考察其特征时间尺度 τv和 τc与流动时间尺度 τf的量级关系,来判断平衡态空气假设是否适用,对应的无量纲达姆科勒(Damköhler)数定义为

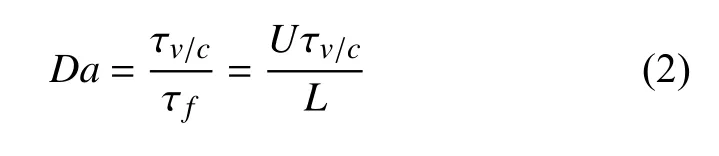
其中L和U是流动特征长度和速度.若Da≫1,则可认为热化学过程来不及发生,流动处于热化学冻结(TC frozen,TCF)态,例如量热完全气体流动;若Da≪1,则热化学过程几乎瞬时完成,流动处于热化学平衡态;若两个时间尺度相当,则流动与热化学过程强耦合,流动处于热化学非平衡(TC non-equilibr-ium,TCNE)态.高超声速流动的速度在千米每秒的量级,若物体几何为米的量级,则 τf在毫秒量级.为评估 τv/c,需建立模型来描述分子内能的能量松弛和有限速率的化学反应过程.以目前的一个常用模型为例,给出O2在不同温度和密度下的 τv/c如图4 所示[48],可见 τv/c跨越了从秒到微秒的量级,且总体趋势为温度越高、密度越大则 τv/c越小.同时,τv与τc可有量级上的差距,所以热和化学过程的状态也可能不同,例如在某些区域流动可能处于热平衡、化学非平衡态.除了O2外,N2等其他组分也有各自不同的 τv/c,所以综合来看,在相当大的温度和密度范围内,流动中均有热或化学过程处于非平衡态.实际上,正如Candler[42]所总结的,典型高超声速高焓流动中流体在激波后、近壁面等速度梯度较大的区域常经历快速的压缩和膨胀,因此很少能有场景可将全场均假设为热化学平衡流进行求解,而须使用非平衡模型.此外,由式(2)知热化学非平衡流动还具有尺度效应,即速度相同时几何尺度越小则流动越趋向热化学冻结态,这也会影响缩比实验的参数设置.

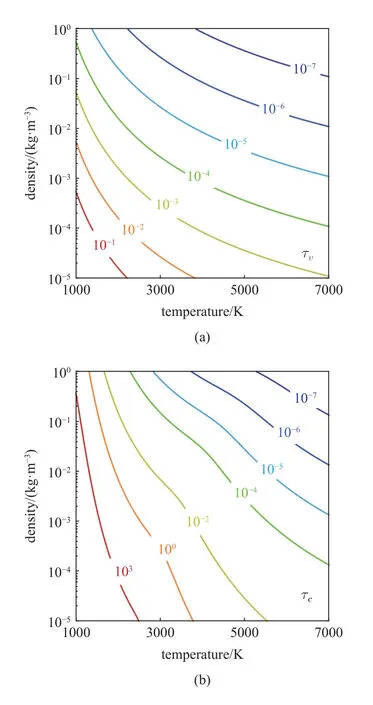
图4 氧气有限速率的(a)振动能松弛和(b)化学分解的特征时间(τ v/c,单位s)[48]Fig.4 Time scales of oxygen of (a) vibrational energy relaxation and(b) chemical dissociation (τ v/c in second) [48]

1.3 热化学非平衡流动方程

热化学非平衡流的求解在物理模型和数值方法上都比平衡流的复杂很多.物理模型上,一方面需要对内能分量松弛和化学反应的速率计算进行建模,这涉及到统计热物理、物理化学等其他学科,另一方面需要考虑有限速率热化学过程与流动的强耦合.目前的主流方法是在NS 方程组中增加振动能、电子能的能量分量守恒和组分质量守恒方程[49-50],来描述不同能量分量和组分质量的产生、对流和扩散等过程.此时分子内能和组分分数等都无法由当地变量唯一确定,而与上下游流场有关.在数值方法上,控制方程组中存在的多个时间尺度会增加方程的数值刚性,带来计算鲁棒性和计算效率方面的问题.相关计算方法方面的研究进展将在第1.4 节中更多介绍.

以下简要介绍热化学非平衡流动模拟中目前主流的以及新兴出现的物理模型.在方程数目上,每一个组分均需要一个组分质量守恒方程.对空气,根据温度范围的不同,常用的组分模型有五组分(N2,O2,NO,N 和O)[51]、七组分(增加NO+和e−)[52]和十一组分模型(增加其他四组分的离子)[50].对火星大气和烧蚀过程等则还需考虑含碳和硅元素的组分[53-54].当组分过多时,也可对组分方程做解耦处理以提高计算效率[55].组分因化学反应的产生和消耗的速率可由化学反应动力学给出,目前应用广泛的模型主要基于Park 等[56-58]在20 世纪80 至90 年代的工作.

对热力学非平衡过程,目前主流的是使用多温度模型,每个温度对应一个独立的内能分量及能量守恒方程.最简化的是Park[59]的双温度模型,即认为分子平动和转动能相平衡、用温度T来计算,而分子振动和电子能相平衡、用温度T ve来计算,这所依据的是不同分量间能量传递的快慢关系.进一步地,可引入更多的独立温度变量来描述不同能量分量间的非平衡关系,例如引入第三个温度来表示电子能的非平衡过程,以及为每个组分的振动能各引入一个振动温度等[60].实际上,以上温度与内能分量的对应关系隐含假设了粒子围绕能态处于准静态分布,而最完整的描述需要将每个内能分量的每个能级均作为一个独立组分变量进行求解,即应用所谓的“态−态(state to state)”方法[61].然而这种方法的计算代价也是巨大的,例如O2和N2就各有47 和68 个独立振动能级,而CO2的独立变量更是可多达1224 个[62].目前这种方法应用到多维流动时计算量仍较大,而且一些简单验证算例显示当介质为空气时,多温度模型也能给出基本相符的结果[63-64].此外,振动非平衡还会与化学反应有耦合效应,已被激发振动能的分子更容易发生分解反应.为表征这种耦合效应,Park[65]引入了一种用T和T ve加权的平均温度来计算分解反应的正向速率,该模型目前的使用较为广泛.近期,势能面和准经典轨迹等方法也被应用到能量松弛和振动非平衡与化学反应耦合效应的研究中[66-67],有望能为热化学非平衡流动计算提供更准确的物理模型.

以空气五组分加双温度模型为例,给出热化学非平衡流动的控制方程组(3),分别如下:连续性方程

其中u=[u,v,w]T是速度,H,E和ev是比总焓、比总内能和比振动能,hs是组分焓,Y s=ρs/ρ 是组分质量分数,R是气体常数;Q t−v和是振动能和化学组分的产生源项.τ是黏性应力张量,qtr和qv是由T和振动温度T v的梯度引起的导热通量,ds是由Ys的梯度引起的质量扩散通量;动量、热量和质量的扩散对应的输运系数分别为黏性系数、热传导系数和质量扩散系数.对相关物理模型的详细描述可参见Gupta等[50]的综述.此外,高焓流场计算还需要有对混合物的热力学与输运参数的拟合[68-69]以及对壁面催化效应的模化[70]等.

1.4 流场求解方法

目前求解高焓流动方程的数值方法已得到较多研究,但在计算模型、数值格式和数据可信度等方面还有很多工作需要开展[71].学者们已发展出多款可模拟高焓流动的计算软件,包括美国宇航局(NASA)的LAURA[72]、GASP[73]和VULCAN 软件[74],以及国内空气动力研究与发展中心(CARDC) 的AERO-PH 和风雷(PHengLEI)软件[75]等.依据对激波的处理方式不同,求解NS 方程可分为激波捕捉法和激波装配法两类.第一类的激波捕捉法通过构造特定的空间离散格式并应用限制器来自动捕捉流场中的间断,适用于求解复杂流动.学者们拓展了多个基于有限体积框架的二阶格式用于热化学非平衡流的计算,包括常规矢通量分裂、AUFS、系数矩阵分裂、Roe 和AUSM 系列等格式[76-79].应用至流动转捩计算时,还需要进一步发展高阶格式,因为一方面对DNS 计算,高阶格式可降低数值耗散和色散,从而更准确地捕捉流场的多尺度时空结构;另一方面对LST 和PSE 等需要高精度基本流的方法,高阶格式可降低所需的网格量,并可避免高马赫流动时物理量二阶导数的数值振荡.针对热化学非平衡流,Wang 等[80]拓展了五阶WENO 格式,Marxen 等[81]发展了六阶紧致差分格式,葛明明等[82]拓展了高阶WCNS 格式,Di Renzo 等[83]开发了使用六阶TENO 格式的HTR 求解器.

第二类是激波装配法,开创性的工作由Moretti等[84]完成,并进一步发展为边界激波装配法和浮动激波装配法两类.图5 是边界激波装配法的示意图,计算域的远场边界始终固定在激波处,边界条件则由Rankine-Hugoniot (R-H)关系确定,从而计算域内部光滑无间断,可应用一致高阶格式进行空间离散,而不需使用限制器.可用的高阶离散格式有谱方法[85]、线性格式[86]和伪谱法[87]等.所以激波捕捉法中存在的激波附近格式降阶和激波后数值振荡等问题可被有效避免,这使得激波装配法在计算简单细长体或钝体外形绕流时具有独特优势[35].此外,激波装配法易于处理扰动与激波的相互作用,因为此相互作用被转化为了一种扰动的边界条件,这对于激波层很薄的高焓流动转捩计算来说尤其重要.此类边界激波装配法也被Prakash 等[88]拓展至了热化学非平衡流动.但与此同时,激波装配法中动网格的使用不可避免,且需额外增加方程来描述激波运动,这些算法的复杂性影响了方程求解的收敛性.针对于此,Chen 等[89]利用广义最小残差(GMRES)和线松弛算法建立了隐式时间推进格式,有效提高了定常层流计算的收敛速度.

图5 边界激波装配法示意图Fig.5 Illustration of the boundary shock-fitting method

当流场中的激波系较为复杂时,边界激波装配法在网格拓扑和计算域分区上存在困难,此时可使用浮动激波装配法.该方法不再需要将激波作为计算域边界,可使用单一计算域处理多个激波或接触间断,域内激波在计算网格上滑动,而激波两侧的物理量仍由R-H 关系确定.浮动激波装配法配合非结构网格在计算复杂流动时取得了很好的效果[90-91].装配法中激波被视为理想间断,这一假设在来流高度较高时由于分子自由程的增加而可能失效.为此可使用如下计算式来预估激波厚度[92]

其中R e∞是单位雷诺数,γ是比热比.取γ=1.4,画出不同来流高度和马赫数下 ∆ 的等值线分布如图6 所示,实际应用时可将 ∆ 与网格尺寸进行对比以判断激波装配法的适用性.

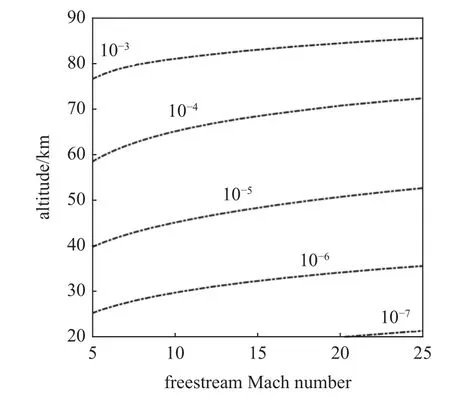
图6 式(4)给出的 ∆ 的等值线Fig.6 Contours of ∆ (unit in meter) from Eq.(4)

激波捕捉和激波装配法都是时间推进解法,需全场联立迭代求解,计算成本较高.对边界层流动,物理量的壁面法向梯度远大于流向,可利用边界层方程的抛物性设计流向推进解法来快速获得边界层剖面,这在边界层稳定性分析中应用相当广泛.目前常用的空间推进法主要有边界层非相似性解法和抛物化NS (PNS)方程法两种.边界层非相似性解法利用Mangler-Levy-Lees 相似性变换[93]进行求解.与量热完全气体时的边界层相似性解不同,由于非平衡源项的存在,即使对平板、尖锥等简单外形,热化学非平衡边界层也不存在相似性解.但是相似性变换消去了边界层方程在原点的奇异性,从而能够流向推进求解[94].边界层非相似性解法仅适用于特定简单外形,且忽略了前缘激波的影响.对于更一般的边界层流动,可利用PNS 方法[95],即对定常NS 方程做抛物化后,基于给定的入口条件推进求解下游流动.当来流马赫数较高时,前缘激波与边界层的黏性干扰会影响空间推进解法的适用性,需要结合算例参数做具体验证[8].

1.5 地面与飞行试验

实验研究主要分为地面高焓风洞实验和飞行试验两类.高焓风洞的典型代表有美国的超高速激波风洞(T5)[96]、国家高能激波风洞(LENS)[97]、德国DLR 高焓激波风洞(HEG)[98]、日本高焓激波风洞(HIEST)[99]及国内中科院力学所的JF 系列风洞[100]和CARDC 的FD 系列风洞[101]等.各种风洞设备的技术原理有所不同,在来流总压总焓、稳定实验时长等参数方面也各有所长[10],其中目前在复现全速域飞行条件方面较为成功的是美国的LENS 系列风洞.LENS 设备是加热轻气体驱动的高焓激波风洞,其中最新的LENS-XX 在以氢气为介质时来流总焓可达到20 MJ/kg (单位雷诺数107m−1时) 至90 MJ/kg (104m−1时),最高来流马赫数超过25,而稳定实验时长在毫秒量级[102].目前LENS 风洞已被成功应用到X43,X51 和HIFiRE 等多种高超声速飞行器的缩比甚至全尺寸试验中[103],也被广泛用于开展高温气体效应、激波/边界层干扰、壁面催化效应和计算程序验证等研究[104-105].

除了地面实验,目前也开展了一些关注高焓边界层的飞行试验,如Reentry-F 再入试验[106]、S-N 再入试验[107]、HIFiRE 项目[108],以及国内CARDC等单位组织的系列飞行试验[109].Tu 等[109]近期综述了与高超声速边界层转捩相关的飞行试验的研究进展,第2.1 节将对相关试验结果做更多介绍.总体来看,先进的高焓气体试验技术是研究高超声速高焓流动非常重要的手段,不过目前仍一定程度上存在实验成本高昂、气动环境恶劣、测量精度受限等问题.

1.6 热化学过程对层流边界层的影响

为方便后续对高焓边界层失稳与转捩特性的讨论,以下以10 马赫的绝热平板边界层[110]为例,来展示热化学过程对边界层剖面的影响.更复杂流动中高温气体效应的影响可参见综述文献[11,43,71].利用边界层方程解法求解方程组(3),给出10 马赫平板边界层中热化学冻结、非平衡和平衡态下的层流剖面如图7 所示,其中冻结和平衡态分别代表了非平衡态在热化学过程极慢和极快时的两个极限状态.由温度剖面,热化学冻结时的壁面温度是平衡态时的近两倍,两者相差近3000 K.而热化学非平衡时的壁温介于两者之间,且表明当地尚未达到振动平衡态(上划线表示基本流物理量);氧气组分剖面也呈现出相同趋势.不同流态时流向速度剖面形状类似,差异主要在边界层厚度,热化学冻结、非平衡和平衡时边界层厚度依次降低,平衡态时名义厚度相较冻结态时减小了24%.

图7 10 马赫绝热平板边界层算例中(a)流向速度,(b)温度和振动温度和(c)氧气质量分数的剖面(R eδ=2000)Fig.7 (a) Streamwise velocity,(b) temperature and vibrational temperature and (c) oxygen mass fraction profiles in a Mach-10 adiabatic flat-plate boundary layer flow

在本算例中,热化学冻结和平衡的边界层沿流向是自相似的,但非平衡边界层沿流向持续变化.画出三种流态中壁面的温度和氧气质量分数沿流向的分布如图8 所示.可见在R ex=0 处,不考虑前缘激波的影响时,热化学非平衡边界层的剖面与冻结时相同,而后向下游发展,振动能被逐渐激发、化学反应逐渐发生,流动趋向于热化学平衡态.为了刻画流动的非平衡程度,引入如式(2)定义的基本流的达姆科勒数写为

图8 壁面物理量随流向的变化: (a)温度和振动温度和(b)氧气质量分数.虚线标注的流向位置对应于图7Fig.8 Distributions of (a) temperature and vibrational temperature,and(b) oxygen mass fraction at the wall.The dotted lines correspond to the location in Fig.7

2 高焓边界层模态稳定性分析

模态稳定性是转捩问题中研究得最早、也是理论最成熟的.目前高焓边界层中针对流向不稳定性的研究最多,而其他类型的不稳定性受到的关注相对较少.同时,现有研究主要考虑空气内发生的热化学过程,而较少考虑壁面催化、壁面烧蚀等的影响.以下分别进行介绍.

2.1 计算方法及实验对比

1991 年,Malik 等[110]最早建立了含有热化学平衡态模型的LST 方法,计算了10 和15 马赫的平板边界层算例.后续Stuckert 等[111]、Bertolotti[112]和Hudson 等[113]相继在LST 中引入了热和化学的非平衡模型.此外,Chang 等[114]最早发展了用于化学非平衡流的线性PSE (LPSE)方法,Ma 等[115]利用DNS 计算了热化学非平衡边界层的扰动模态增长.回顾图1,在流动转捩重要的区域电离反应的影响一般较小,因此目前大多数高焓边界层转捩计算中只考虑振动能和组分分解反应的影响.近期,Miró Miró等[116]以火星大气为背景,将电离反应模型引入了LST,计算了来流马赫数高达45 的楔体边界层算例,该算例中电离反应对主导的第二模态有显著影响.值得说明的是,以上方法均是考虑了热化学过程与扰动的强耦合,即同样推导了振动能(及电子能)和组分方程的扰动形式,扰动方程组的基本变量数与方程组(3)中基本流方程的变量数相同.

在实验方面,1994 年,He 等[117]在T4 风洞中测量了高焓平板边界层的转捩雷诺数R etr,来流在6 马赫左右而最高总温达到9100 K.他们发现随着来流焓值的提高,高温热化学过程与壁面冷却一样都降低了R etr,即促进了转捩.Germain 等[118](以及Adam 等[119])在T5 风洞中以6 马赫左右的来流实验了四种气体: He、N2、空气和CO2,这四种气体发生热化学过程的临界温度依次降低.实验He 时(最大Ma∞达到11.9)R etr几乎不随来流总焓变化,而实验CO2时R etr随总焓快速升高,显示出热化学过程推迟了转捩.Johnson 等[120]利用热化学非平衡假设的LST 重复出了该实验中的转捩变化趋势,并确认主导模态仍是第二模态.

利用LST 和LPSE 方法,美国明尼苏达大学的Candler 团队开发了以PSE-Chem 求解器为核心的STABL 软件,用于高焓边界层的模态失稳分析与eN方法转捩预测[121-122].有类似功能的软件还有NASA 的LASTRAC[123]和比利时冯卡门研究所(VKI)的VESTA[124]等.天津大学罗纪生和曹伟团队也开发了高焓边界层的LST 和LPSE 的计算程序,并重点研究了热化学平衡态边界层的稳定性特性[125-127].利用这些软件可开展与高焓流动实验结果的对比,进而验证计算模型并得到转捩起点处的N值.例如Malik[128]用化学非平衡模型分析了Reentry-F 和S-N 再入飞行试验数据,两组算例的来流马赫数均超过了20,计算发现转捩由第二模态主导,转捩N值为9.5～ 11.2.对其中的Reentry-F 算例,化学非平衡效应对第二模态有激发效果,使得转捩起点由流向4.4 m 提前到了3.1 m.针对高焓风洞转捩实验的结果,学者们也开展了大量的线性稳定性分析,所用风洞数据来自包括T5[129],LENS[130],HIEST[131],VKI-Longshot[132]等,结果显示稳定性计算获得的第二模态的主导频率和增长率等都与实验数据基本相符,关联得到的转捩N值在5～ 8 左右.

2.2 第三模态与超声速模态

在高焓边界层的流向不稳定性中,有两个模态的作用更加重要,一个是第三模态,一个是超声速模态.图9 给出了来流20 马赫、半顶角为7°的热化学非平衡钝锥边界层算例的中性曲线[133],可见在相比第二模态更下游和更高频的区域出现了不稳定的第三模态,这是高马赫数边界层的重要特征[18].第三模态和第二模态均属于Mack 模态,且均源于快模态与慢模态的同步过程[134].该算例给定的壁温远低于绝热壁温,因而第一模态受到抑制而第二与第三模态均受到激发,第三模态的最大增长率约为第二模态的一半.最不稳定的第一模态是三维的,而第二与第三模态的增长率随着周向波数的增加均下降.虽然第三模态有较大的增长率,但该算例中的N值包络仍主要由第二模态贡献.

图9 扰动增长率等值线: (a)轴对称(零周向波数)模态和(b)三维模态,算例为来流20 马赫的热化学非平衡钝锥边界层[133]Fig.9 Growth rate contours of (a) axisymmetric and (b) 3D modes in a Mach-20 TCNE blunt-cone boundary layer[133]

除了Mack 模态以外,近年来在第二模态下游区域出现的不稳定的超声速模态引起了学者们的广泛关注.所谓超声速模态,是依据扰动的相对马赫数Mar做的划分,三维和二维(展向波数β=0)扰动的Mar分别写为[18]

在量热完全气体边界层中,超声速模态一般是稳定的,但在极低壁温条件下也可能变为不稳定[135].在高焓边界层中,由于热防护的需要,设置的壁温一般远低于绝热壁温,同时高温热化学过程进一步降低了边界层温度,所以不稳定超声速模态更为广泛地出现,在热化学平衡[111]和非平衡[114]算例中均有报道.Bitter 等[121]基于风洞条件(来流5 马赫、静温1500 K),计算了300 K 极冷壁的振动非平衡平板边界层,发现第二模态下游出现的不稳定超声速模态扩大了不稳定频率区间.Knisely 等[136]利用DNS 研究了热化学非平衡圆锥边界层中的超声速模态,并重点关注了壁温的影响.Han 等[137]通过分析远场均匀流的色散关系,提出了一种基于扰动群速度方向的新的扰动远场边界条件,继而发现超声速模态实际有两类,一类向远场辐射,另一类向壁面传播,并发现了超声速模态形成的两种方式.Chen 等[138]利用LPSE 研究了热化学非平衡效应、壁温和频率等对超声速模态演化的影响.

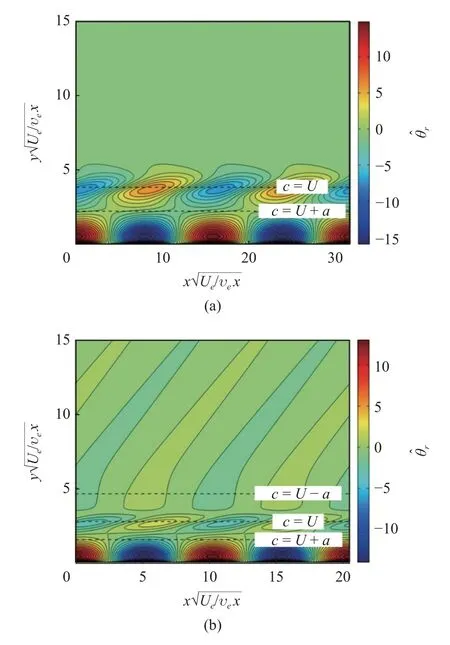
图10 (a)亚声速和(b)超声速模态的温度扰动等值线,算例为5 马赫振动非平衡平板边界层[121]Fig.10 Temperature disturbance contours of (a) subsonic and(b) supersonic modes in a Mach-5 vibrational non-equilibrium flat-plate boundary layer [121]

总体来看,在以上算例中,不稳定超声速模态虽然受到冷壁条件和热化学过程的激发,但增长率仍较低,N值包络仍由第二模态主导.相比之下,Mortensen[139]利用LST 和DNS 发现增加钝锥的钝度对超声速模态有强烈的激发效果.在他计算的来流20 马赫、高度26 km 的热化学非平衡钝锥算例中,当球头半径增加到35.6 mm 时,超声速模态的增长率超过了第二模态(见图11),使得基于eN方法预测的转捩起点向上游移动了0.8 m;当钝度进一步增加时,超声速模态均为主导模态.总体上看,目前对第三模态和超声速模态的研究还不够充分,其在转捩中的具体作用还有待进一步研究.

图11 大钝度圆锥边界层中失稳模态的增长率特征[139]Fig.11 Disturbance growth rate behaviors in the cone-boundary-layer case with large nose bluntness[139]

2.3 热化学过程对第二模态的影响规律

早期不同学者得到的热化学过程对第二模态的影响规律似有相互矛盾之处,例如Bertolotti[112]的结论为振动非平衡对第二模态有较大激发作用,而Hudson 等[113]的结果表明振动非平衡对第二模态有稳定作用.实际上,这很大程度上是因为不同学者使用的高温气体模型有区别,包括不同的热力学系数、输运参数、化学反应系数和能量松弛模型等.为此,后续学者们在两个方向开展了大量工作,第一是通过控制变量法区分出各类模型的影响,第二是进行理论推导以寻找关键影响参数.

在第一个方向,即气体物理模型的影响方面,Lyttle 等[140]研究了不同的组分焓拟合式、输运参数模型和化学反应速率等对第二模态的影响,算例是13.5 马赫的钝锥绕流.他们的结果表明不同组分焓拟合式的影响很小,而输运参数模型的影响最大.Franko[141]和Miró Miró等[142]也得到了相同的结论,并且发现使用不同的输运参数模型时转捩位置(基于eN方法)的偏差最大分别可达50%和38%,该偏差甚至大于非平衡和平衡态边界层间的差别;化学反应速率模型有一定影响,而质量扩散和反应平衡常数模型的影响很小.

在第二个方向,学者们通过系列工作基本理清了热化学过程对第二模态的影响.以下仍基于第1.6 节中的10 马赫的绝热平板边界层算例进行说明.图12 给出了基于图7 的基本流的热化学冻结、非平衡和平衡态下扰动的模态增长率随频率的变化.可见三种流态下均是第二模态有最大的增长率,且在高频时存在不稳定的第三模态.不同流态边界层的增长率和相速度曲线之间有明显区别.从热化学冻结到非平衡态,第二模态的最大增长率和对应频率均有增加,这与量热完全气体边界层中降低壁温引起的趋势相同[111],因为非平衡效应同样降低了边界层温度和厚度.从非平衡到平衡态,尽管边界层温度和厚度继续降低,但增长率曲线的变化趋势却有不同: 第二模态的最大增长率稍有增加,而频率反而小于非平衡态时.以上不单调的变化规律说明仅考虑基本流的变化无法给出完整的规律解释.

图12 10 马赫绝热平板边界层中二维模态的(a)增长率和(b)相速度随圆频率的变化(R eδ=2000)Fig.12 (a) Growth rate and (b) phase velocity of the 2D mode in a Mach-10 adiabatic flat-plate boundary layer

实际上,除了由层流变化引起的失稳特性的改变外,扰动传播时也会引起新的热化学过程,该过程通过非平衡源项的扰动项同样影响扰动特性[120].声学经典理论显示在均匀自由流中,扰动引起的非平衡过程产生两个影响[143],对吸热过程(冻结声速大于平衡声速)会降低扰动传播的声速和耗散声波的幅值,对放热过程则作用相反;基于无量纲数 ω τv/c,同样可对扰动也做冻结、非平衡和平衡态的区分.若流动中存在多个不同的 τv/c,则可利用Fujii 等[144]发展的框架做数值求解,以得到不同频率扰动的声速和声波幅值耗散率.以图7 中壁面附近的流动参数为例(温度3000 K、密度0.003 7 kg/m3),画出压力扰动幅值的耗散率随扰动频率的变化如图13 所示.可见耗散率最大时对应的频率为0.011 kHz,与图12 中第二和第三模态的频率范围相差超过三个量级,所以在第二和第三模态频率范围内耗散率已降至千分之一左右,扰动已进入热化学冻结态的范围,幅值耗散的影响很小.此外,当温度越高,则热化学非平衡扰动区域越向高频方向移动.

图13 自由来流中热化学非平衡扰动的幅值衰减速率,第二和第三模态的频率范围取自图12Fig.13 Amplitude dissipation rate of disturbance in the uniform free-stream;the frequency ranges of the second and third modes are from Fig.12

将以上均匀自由流中的结论应用至边界层的扰动分析.首先,无黏扰动方程分析显示声速和相对马赫数同样是热化学非平衡和平衡边界层的Mack 模态的关键参数[145].扰动非平衡过程在不改变基本流的情况下降低了声速,使得第二模态更不稳定且对应频率下降,而扰动幅值的耗散引起增长率的下降[48].进一步地,Bitter[146]基于无量纲数 ω τv/c,通过与边界层厚度相关联,得到边界层中扰动的达姆科勒数为

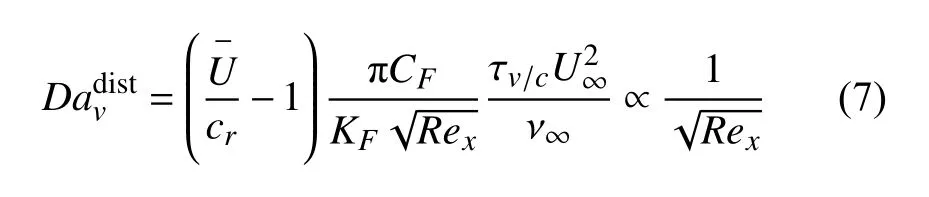
其中,C F和K F是关联系数,衡量了扰动的非平衡程度.与式(5)相比,沿流向下降得更慢,因此一个重要的结论为扰动相比基本流更趋向于热化学冻结态.这一结论由图14 展示得更清晰: 在基本流的非平衡区,扰动可能仍处于冻结态;当基本流已达到平衡时,扰动可能仍为非平衡.对前一种情况,基于非平衡的基本流使用量热完全气体的稳定性分析求解器也能给出基本相符的结果[120-121],这样的弱耦合解法能够提高稳定性分析的计算效率.对后一种情况,由于扰动处于非平衡态,弱耦合解法的结果会有较大偏差.此外,图14 也表明假设“基本流为非平衡态,而扰动为平衡态”是不符合物理过程的.

图14 振动非平衡边界层中层流(基本流)和扰动的达姆科勒数的量级变化示意图[146]Fig.14 Illustration of the distribution of the mean-flow and disturbance Damköhler numbers in a vibrational non-equilibrium boundary layer [146]

由上述讨论,总结热化学非平衡效应对第二模态的影响如表1 所示,最终的影响效果是两个作用的叠加.由此,图12 中从热化学冻结态向平衡态的变化趋势可以被解释[48]: 一方面,边界层温度和厚度下降引起第二模态的增长率变大、对应频率升高;另一方面,由于非平衡源项的扰动项,扰动传播的声速降低,引起第二模态的增长率升高、对应频率降低.两个作用叠加后,热化学平衡边界层的第二模态相比冻结态时更不稳定,但频率可能相接近,因为两个作用对频率的影响是相反的.

表1 热化学非平衡效应对第二模态的影响汇总Table 1 Summary of the influences of TCNE effects on the second mode

对给定算例,计算表1 中的关键参数可判断两个作用的影响程度.综合来看,高超声速边界层中第二模态失稳的典型频率一般在100 kHz 的量级,五组分空气模型中此频率的扰动在较大密度和温度范围内均接近热化学冻结态(见图13),因此作用二的影响一般较小,而作用一占主导,即热化学非平衡效应主要是通过修正基本流剖面来影响边界层的模态稳定性,使得第二模态更不稳定、频率升高.Chen等[147]进一步从扰动能量输运机制的角度开展了分析,指出热化学非平衡与量热完全气体边界层中第二模态增长率的差异主要源于基本流法向梯度引起的产生项.

需要特别指出,CO2的热化学特征时间比空气的低若干数量级,因此若混合物中含有较大比例的CO2,例如计算物面烧蚀或火星大气层,则作用二可能有很大影响[112,148],与作用一叠加后仍可使得第二模态更稳定,此时需重新评估D advist.此外,Miró Miró等[116]发现电离过程对层流的改变同样使得第二模态更不稳定,但引起的作用二有很大的稳定效果,两者叠加后仍使得第二模态增长率降低.

2.4 壁面效应与转捩控制

目前大多数高焓边界层转捩计算的壁面边界为“理想”边界,既不考虑壁面对流体反应的催化作用,也不考虑壁面烧蚀过程.目前已有一些描述壁面−气体相互作用、界面非均相反应和烧蚀效应的计算模型[149],但对这些壁面反应如何影响转捩的研究总体上还较少.Klentzman 等[150]研究了壁面催化效应对模态稳定性的影响,发现壁面催化对第二模态有一定的稳定作用.Mortensen 等[151-152]将壁面烧蚀反应引入LST 的框架,计算了热化学非平衡的十一组分模型(空气五组分加上含碳元素的组分),其中壁面质量引射引起了类似壁面吹气的效果.该16 马赫的钝锥边界层算例中模态失稳仍由第二模态主导,并且他们发现壁面吹气对第二模态有激发效果,而含碳组分的产生则有轻微的稳定效果.后续Miró Miró等[153]进一步开展了参数化研究,区分出了烧蚀诱导的质量引射效应、烧蚀和辐射诱导的壁面冷却效应、含碳组分分解、壁面反应等过程对第二模态增长率和N值的影响,发现前两个效应的影响很小,而空气组分的振动松弛过程影响最大.李瑾等[154]系统研究了质量引射速度幅值、引射区域宽度、中心位置、组合以及体积流量等因素对第二模态的影响,总结了相关影响规律.

高焓边界层的转捩控制研究也逐步得到开展.热化学过程使得以CO2为介质的流动中的第二模态更稳定,由此Leyva 等[155]利用实验和数值手段发现向流动中注入CO2可推迟转捩;当CO2的体积分数达到40%时,转捩雷诺数增加了超过一倍.Johnson等[156]还研究了壁面吹吸的影响,Wang[157]发现使用壁面多孔敷层同样能使得热化学非平衡边界层中的第二模态更稳定.在此方向,粗糙单元、波纹壁、局部加热/冷却等一些经典的转捩控制手段[158-159]在高焓边界层的应用研究还有待开展.

2.5 三维边界层稳定性

三维边界层中的转捩机理相比二维时更加复杂,且其对于实现对飞行器构型的转捩预测有至关重要的意义.总体上看,目前对高焓三维边界层稳定性的研究还较少,近期针对横流模态和粗糙单元后的尾迹流失稳有一些研究进展.2018 年,Kline 等[123]使用LST 计算了一个13 马赫来流的后掠翼边界层算例,并发现绝热壁面条件下化学非平衡效应对定常横流涡的线性增长有稳定作用.与之相对应,近期Chen 等[160]计算了16 马赫的后掠抛物体边界层算例,发现热化学非平衡效应使得横流模态更不稳定,并解释了横流马赫数是其中的关键参数.他们还进一步利用二次失稳理论计算了饱和定常横流涡(见图15)的二次失稳,发现量热完全气体算例中最不稳定的二次失稳模态是位于上洗区的传统的I 型(z)模态,而热化学非平衡算例的结果则不同,最不稳定的模态位于横流涡的下洗区.

图15 16 马赫的热化学非平衡后掠抛物体边界层中定常横流涡的演化[160]Fig.15 Evolution of the stationary cross-flow vortices in a Mach-16 TCNE swept-parabola boundary layer [160]

2017 年,Stemmer 等[161-162]考虑化学非平衡利用DNS 计算了含有长方体型粗糙单元的流动,并计算了尾迹流的失稳模态.他们发现奇模态是尾迹流的主导模态,并通过与量热完全气体和化学平衡算例的比较,发现化学非平衡效应对模态增长率有明显影响,在计算中应当被考虑.Di Giovanni 等[163]进一步用DNS 计算了来流20 马赫的半球形几何上的粗糙单元流动,并分析了尾迹流中的y和z等失稳模态,结果显示热化学非平衡效应有显著影响而需要被考虑.近期,Demange 等[164]发展了考虑热化学平衡模型的全局稳定性方法,分析了射流的全局失稳模态,发现热化学平衡算例中预测的失稳模态增长率显著更高,且振荡频率等流动特征有明显不同.在此方向,对离心和前缘等不稳定性[165-166]的研究还有待深入开展.

3 感受性、瞬态增长与非线性作用

3.1 感受性

边界层转捩的结果严重依赖于外界扰动,感受性研究便是要找出自由来流扰动与边界层内激发的不稳定波之间的定量对应关系,即给出边界层内扰动演化的初值[12,167].均匀自由来流的扰动一般能表达成涡波、熵波和声波(包括快声波和慢声波)这三种基本扰动的组合,感受性研究也一般针对这三种基本扰动展开.Ma[168]基于10 马赫平板边界层算例,研究了热化学非平衡效应对第二模态感受性的影响.他们在自由来流中分别施加这三种基本扰动,发现热化学非平衡流中扰动激发第二模态的过程均与量热完全气体时基本相同(包括扰动与激波的相互作用、模态同步与演化等),而感受性系数更大,即当来流扰动幅值相同时激发出的第二模态幅值更大;这样的激发作用被归因于热化学非平衡引起的壁面冷却效应.后续Klentzman 等[150]以及Edwards等[169]也研究了化学非平衡平板边界层的感受性,均关注第二模态.相比之下,其他模态的感受性特性仍有待系统性研究.

3.2 瞬态增长

瞬态增长是一种由线性机制主导的非模态增长,存在于多条实际转捩路径中[14];其数学上是源于控制方程中线性算子特征值的非正交性.Franko 等[170]计算了化学平衡态边界层的最优瞬态增长,发现其明显强于化学冻结态时.Bitter[146]分析了平板边界层中模态增长与瞬态增长这两种机制的相对重要性,发现来流马赫数在2.5 及更低时,两种机制引起的扰动增长倍数相当,或后者更高;而当来流马赫数提高至5 时(边界层外缘温度为1000 K～ 1500 K,考虑振动非平衡效应),在预估转捩位置处扰动模态增长的倍数要高出若干数量级,这提示在高超声速边界层中瞬态增长机制的重要性相比低速边界层时可能下降了.

3.3 非线性作用与转捩机制

当小扰动经历模态增长到较大幅值后,扰动方程中的扰动二阶项(如雷诺应力项等)不可忽略,非线性作用逐渐产生重要影响.目前针对高超声速及更低速边界层的研究表明,对流向不稳定性,波共振(wave resonance)机制在扰动非线性演化初期起决定性作用,按共振机制和起主要作用的扰动模态的组合划分,流动转捩主要有三种类型: K 型(基本共振是主导机制)、N 型(亚谐共振是主导机制)和O 型(初始一对斜波模态主导)[171-172].实际情形中可能有好几条转捩路径同时起作用.在这三种转捩的后期,流场内有基本一致的物理机制与特征结构,包括发卡涡、尖峰和相干结构的生成与演化等[173-174].对三维边界层,横流涡以及Görtler 涡的二次失稳过程会诱发从低频到高频的快速增长的扰动[22,175-176],在转捩后期的强非线性阶段同样存在相干结构和发卡涡等[177].

目前对高焓边界层中扰动的非线性演化和转捩后期流场的研究还较少,这是近年的热点研究领域.2009 年,Linn 等[178]利用DNS 研究了6.8 马赫的平板边界层中第二模态的基本共振,发现振动非平衡模型得到的共振幅值低于量热完全气体和振动平衡模型.Marxen 等[179]利用DNS 计算了10 马赫绝热平板边界层中第二模态的二次失稳与基本共振过程,发现化学非平衡效应主要是通过改变首次失稳特征来间接影响二次失稳,当首次失稳扰动幅值相同时对二次失稳扰动的影响很小.Zanus 等[180]则在热化学平衡态假设下利用非线性PSE (NPSE)计算了同样的算例.近期,Chen 等[133]发展了针对热化学非平衡流的NPSE 和二次失稳分析方法,计算了第二模态的二次失稳过程,发现基本共振是二次失稳的主导机制,且热化学非平衡效应使得基本共振的增长率更大.Zanus 等[181]还进一步研究了NPSE 计算非平衡边界层时非线性项阶数、输运系数高阶导数等因素的影响.此外,Chen 等[182]以15 马赫的热化学非平衡钝锥边界层为例,用NPSE 计算了由一对第二模态斜波引起的O 型转捩,并发现热化学非平衡效应通过激发第二模态使得流向涡及其他模态的增长均更快.

2021 年,Di Renzo 等[183]利用DNS 首次计算了化学非平衡边界层从层流失稳一直到全湍流的过程(见图16),其中转捩机制主要是二维第二模态的二次失稳.他们重点关注了breakdown 至全湍流段的平均流剖面演化,以及脉动一阶和二阶统计量的分布.刘朋欣等[184]也考虑化学非平衡效应对湍流做了DNS 研究,检验了经典标度率的适用性,并发现化学非平衡效应对密度平均后的雷诺应力分布影响不明显.此外,吴正园等[185]、Passiatore 等[186]也开展了热和化学非平衡的湍流DNS 研究,这为进一步开展湍流建模研究提供了基础性支撑.

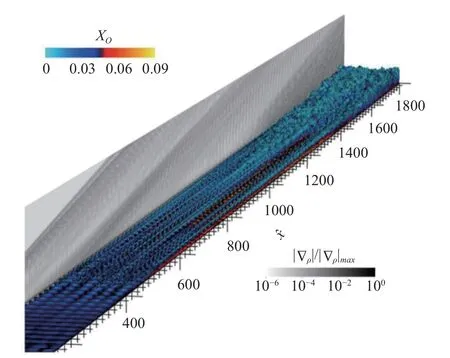
图16 10 马赫化学非平衡平板边界层中由氧原子的体积分数着色的Q 的瞬时等值面[183]Fig.16 Instantaneous Q-isosurface colored by oxygen mass fraction in a Mach-10 chemical non-equilibrium boundary layer[183]

4 结论与展望

本文主要介绍了近年来在高温气体物理模型、高焓流动计算方法、高焓风洞与飞行试验技术、流动失稳与转捩机理等方面的研究进展.总结来看,主要进展如下.

(1) 基于高温气体物理模型,通过拓展NS 方程,已基本建立了求解高焓热化学平衡和非平衡流动的各类高精度数值格式,发展了相应的激波捕捉、激波装配和边界层方程解法,其中应用隐式时间推进格式可有效克服热化学非平衡流动的强数值刚性并提高计算效率.已基本建立了考虑高温热化学过程的包括DNS,LST,PSE,SIT 等在内的流动稳定性与转捩分析方法.

(2) 高焓风洞设备以及飞行试验技术得到了快速发展,相关试验结果已被广泛用于研究高温气体物理模型和边界层转捩.线性稳定性分析方法给出的高焓边界层主导模态的增长率、频率等能与实验结果基本相符.高焓风洞数据关联出的转捩N值在5 至8 左右.

(3) 高超声速高焓二维边界层失稳仍主要由第二模态主导,但在部分高马赫和大钝度的边界层算例中出现了较大增长率的第三模态和超声速模态.对空气五组分模型,热化学非平衡效应一般使得第二模态更不稳定.对三维边界层失稳以及扰动演化的感受性、瞬态增长和非线性增长阶段,热化学平衡和非平衡效应均有重要影响,在横流涡二次失稳等流动中甚至改变了主导失稳模态.

(4) 高焓流动中壁面催化、壁面烧蚀等效应对边界层失稳与转捩的影响研究得到重视和逐步开展,其中壁面烧蚀过程给转捩带来了复杂影响,包括为流动引入额外组分、引起壁面质量引射、改变壁面形状产生粗糙单元结构等,且影响趋势强烈依赖于算例参数.在转捩控制技术方面,CO2注射、多孔敷层、壁面吹吸等手段已得到研究,这些控制手段展现出稳定第二模态、推迟转捩的能力.

高超声速高焓流动转捩问题是涉及多物理场的复杂过程,目前仍有很多需要解决的问题,未来研究工作至少包括以下方向.

(1) 发展适用于高超声速高焓边界层的湍流模拟方法,以及湍流和转捩模式理论.受限于计算能力,目前对实际飞行器的全机流场计算仍离不开湍流与转捩模式方法,然而当前对高超声速高焓边界层湍流与转捩的建模研究还非常有限,模式发展与改进仍面临一系列问题,包括但不限于: 目前建模所需的实验或DNS 基础数据仍较少;控制方程中新增的质量扩散、能量松弛、化学反应等过程引起的脉动如何有效模化？第三模态、超声速模态等的作用如何体现？当来流马赫数在10 以上时,密度和温度脉动幅值可比速度脉动高出一个量级,仅用动能是否能合理反映转捩和湍流中的脉动能量？

(2) 与其他学科交叉以进一步完善已有的高温气体物理模型,这需要与物理化学、电磁学、材料学等多学科学者的共同努力.特别地,壁面烧蚀和壁面催化在实际飞行过程中难以避免,而目前仍缺少能准确描述这两种过程与流动耦合效应的模型,也缺少相关实验验证.此外,如第1.3 节所述,目前出现的一些新兴的先进气体模型计算效率仍较低,需要研究这些模型如何能与计算流体力学更有机结合并有效拓展至多维流动计算.

(3) 开展高超声速高焓三维复杂边界层的失稳与转捩的分析方法和机理研究,并创新转捩控制手段,这对飞行器的设计与优化有重要的应用价值.具体来说,全局稳定性分析方法在高焓边界层中的应用还很少,高温气体效应对三维边界层中接触线模态、Görtler 模态、剪切层模态等的影响规律还不明晰,这些模态的感受性特性也仍待研究,以及需要探究更好的转捩控制手段以改善飞行器面临的恶劣气动环境.此外,由于高焓条件下影响因素众多,系统性的参数研究和数据库的建立与完善也是非常重要和紧迫的.