基于定常吹吸气的波浪型圆柱主动控制研究1)

邹 琳 左红成 柳迪伟 王家辉 徐劲力

(武汉理工大学机电工程学院,武汉 430070)

引言

当前化石能源短缺问题日趋严重,风能作为一种新型绿色能源有着广阔的应用前景[1-2].对于风能的获取,相较于传统大型风力发电机通常放置在沿海、近海和其他高风速地区,如无叶片风机[3]、MEMS 风力俘能装置[4]等发电设备利用涡激振动进行发电,可进行小型化设计并可用于低风速地区,适合作为无线传感器网络系统的能源利用和郊区、农村环境以及远离电网系统的偏远地区的小型电力系统[5],如何诱导更激烈的振动响应是提升风能利用效率的关键.

国内外学者针对圆柱近尾迹流动进行控制来达到减振或者增振的目的,流动控制方式主要分为被动控制和主动控制[6],被动控制主要通过改变表面形状或者在钝体周围安装附加装置来干扰剪切层分离来达到控制效果,由于不需要能量输入,应用较为广泛,如分离盘[7]、螺旋列板[8]、附属柱体[9]等.近年来学者亦通过改变圆柱表面形状来影响圆柱周围的流动结构,Lam 等[10]在Re=100 针对λ/Dm=1～10,a/Dm=0.05～ 0.25 一系列不同波幅和波长的波浪型圆柱进行研究,得出波长和波幅两个参数对升阻力系数的影响规律,随后Bai 等[11-13]和Lin 等[14]在Re=3000 通过数值模拟和PIV 实验系统分析了波长对波浪型圆柱流动特性的影响,研究发现λ/Dm=6.06 的波浪型圆柱Node 截面流动分离较早,产生的额外流向涡附着到柱体表面起到稳定剪切层作用,在波浪型圆柱下游出现“夹状涡”,平均阻力系数较直圆柱降低了93%;Zhang 等[15]研究波浪型圆柱的涡特征发现Node 截面和Saddle 截面之间的流场分布存在强烈的三维效应,波浪型圆柱后流场出现“肋状涡”;赵桂欣等[16]通过对12 种单自由端波浪型圆柱进行大涡模拟发现大多数组合能降低平均阻力系数,但在特定波长,脉动升力系数较直圆柱有所增加;吴应湘等[17]通过对波动柱进行实验和数值仿真发现雷诺数从100～ 10 000 变化时,波动柱的平均阻力系数随着波动强度的增大而增大,而脉动升力系数则是先减小再增大,并且在更高折合流速下振幅相较于直圆柱显著增大.由此可见,特定波浪型圆柱的脉动升力系数较直圆柱可能有所提升.

吹吸气作为一种主动控制方式对流动分离有着显著的控制效果[18-19],国内外学者通常针对圆柱进行减阻减振控制,Chen 等[20-21]通过实验和数值模拟在圆柱分离点沿展向布置有限数量吸气孔,在特定间距布置时发现相邻孔之间产生一对反向旋转的三维涡,平均阻力系数和脉动升力系数较未受控时降低,并且实验表明吹吸气速度与来流速度之比小于1 控制效果较好,Kim 等[22]采用分布力控制方法在圆柱分离点施加沿展向正弦变化的定常吹吸气,发现分布力同相位时能够有效减小圆柱阻力,Feng等[23-24]发现通过在圆柱前后驻点沿展向狭缝进行吹吸气能起到虚拟气动外形作用,并与圆柱剪切层相互作用能诱导新的尾涡模式,圆柱下游尾流旋涡由交替脱落模式变成对称脱落模式;在增振方面,Mei等[25]发现当在圆柱分离点吹气和前驻点吸气时,圆柱的阻力和升力系数波动幅度分别增加了785.71%和139.62%,陈文礼等[26]在Re=300 下在圆柱前后驻点处进行4 种组合的定常吹吸气,发现前后吸气和前吹气后吸气时圆柱的脉动升力系数显著增加.由此可见,圆柱控制效果受吹吸气方式、方位角和吹吸气动量系数影响,在特定吹吸气工况下能显著增强圆柱的脉动升力,从而诱导更强烈的振动.

综上所述,前人的研究发现改变柱体表面形状、定常吹吸气等控制方法对圆柱无论是增振还是减振都有着较好的控制效果,而波浪型圆柱由于表面形状影响,流动结构较圆柱发生改变,吹吸气控制方式对波浪型圆柱的近尾迹流动控制效果尚不清楚.本文设计在波浪型圆柱前后驻点处沿展向狭缝进行定常吹吸气,采用大涡模拟在亚临界雷诺数(Re=3000)下研究前吹气后吸气和前后吸气在不同吹吸气动量系数下对波浪型圆柱流动结构的影响,揭示定常吹吸气作用在波浪型圆柱的流动控制机理,为低风速地区分布式风力俘能结构俘能效率的提升提供有益探索.

1 数值方法

1.1 控制方程

大涡模拟(large eddy simulation,LES)采用空间滤波技术[27],通过截止尺度和滤波函数将涡识别为大尺度涡和小尺度涡,在数值模拟中直接解析大尺度涡,小尺度涡对大尺度涡的影响则通过亚格子尺度应力模型(subgrid scale stress,SGS)封闭求解,经滤波函数处理后的不可压缩的Navier-Stokes 方程为

式中,xi,yi为笛卡尔坐标;i,j=x,y,z;ui,uj为滤波后的速度;为滤波后的压力;τij为亚格子尺度应力;ρ和ν分别表示流体介质的密度和运动黏度.

为使计算方程封闭,采用Smagorinsky-Lilly 亚格子模型[28]计算亚格子应力τij

式中,δij表示Kronecker 增量,τkk是SGS 应力的各向同性部分,νsgs表示SGS 涡流黏度,表示解析场中的应变张量

式中,∆ 表示过滤的网格尺度,Cs为Smagorinsky 常数,研究者发现广泛的流动中Cs=0.1～ 0.14 可以取得较好的数值仿真结果,本文取0.1[29].

1.2 控制方程离散

本文计算控制方程离散均采用有限体积法,所有仿真使用双精度计算,压力−速度耦合采用PISO算法,动量离散采用二阶中心差分格式,时间离散采用二阶隐式格式[29].

2 计算模型及网格

2.1 模型简介

未受控波浪型圆柱如图1 所示,其几何表达式为

图1 波浪型圆柱的几何模型示意图Fig.1 Geometric model of the wavy cylinder

式中,Dz表示波浪型圆柱对应高度z上的直径,Dm=0.01 m 表示波浪型圆柱的平均直径,Dmax为波浪型圆柱最大直径,Dmin为波浪型圆柱最小直径,Node 代表波浪型圆柱的最大截面,Saddle 代表波浪型圆柱的最小截面,Middle代表波浪型圆柱Node 与Saddle 之间的中间截面,Lz为波浪型圆柱展向高度,a和λ分别表示波浪型圆柱的幅值与波长.Lam 等[29]指出a/Dm=0.091,λ/Dm=2.818 的波浪型圆柱近尾迹混乱无序、不稳定,受到外部扰动可能会增强脉动升力,故选取该参数波浪型圆柱作为研究对象.

2.2 计算域及网格划分

参考Lam 等[29]计算域大小和边界条件设置,本次仿真的计算域大小为24Dm× 18Dm× 5.636Dm.X轴正方向为顺流向,Y轴为横流向,Z轴为波浪型圆柱展向,笛卡尔坐标系圆心位于波浪型圆柱中心.上游入口处边界距离波浪型圆柱中心为8Dm,下游出口处边界距离波浪型圆柱中心为16Dm,展向高度为2λ.入口采用速度入口(velocity-inlet),来流速度U∞=4.382 2 m/s,出口采用压力出口(pressureoutlet),背压设置为0 Pa,计算域两个侧面采用对称边界条件(symmetry),波浪型圆柱沿展向设置周期性边界条件,波浪型圆柱表面设置为无滑移壁面(no-slip-wall).流体介 质为空气,密度ρ为1.225 kg/m3,运动黏性系数ν为1.789 4 × 10−5m2/s.无量纲时间步长∆t*=U∞∆t/Dm,U∞为来流速度,∆t为时间步长,本次大涡模拟计算中,取∆t*=0.005,计算出库朗数约为0.833,满足CFL 条件.

本文使用ICEM 对计算域进行结构化网格划分,利用O-block 技术对圆柱周围加密,避免了片状低质量网格的生成.大涡模拟对于边界层的要求控制y+≤ 1,对圆柱周围进行3Dm× 3Dm指数形式增长的区域加密,计算域及其网格划分如图2 所示.

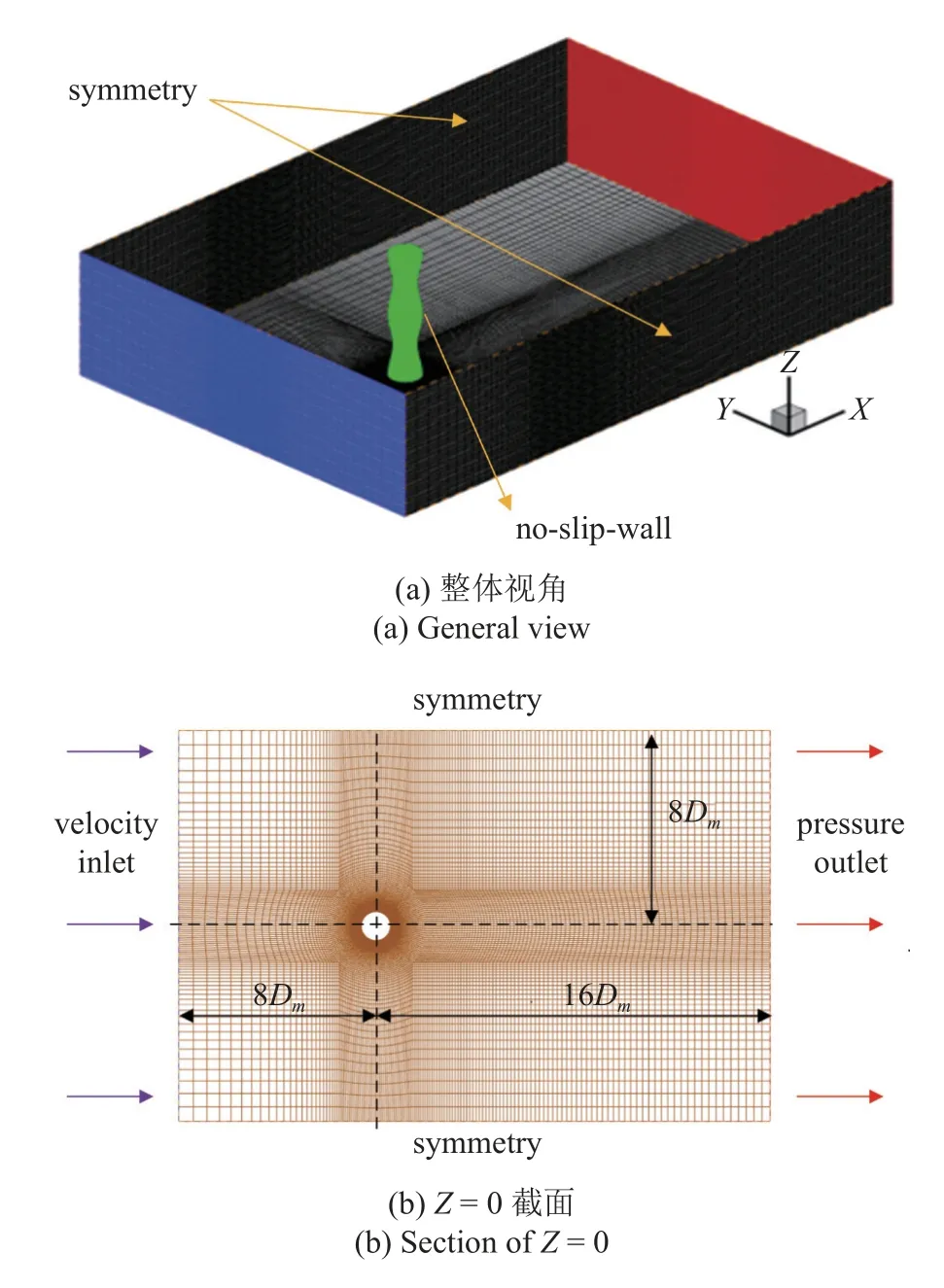
图2 波浪型圆柱计算域及网格示意图Fig.2 Schematic diagram of calculation domain and grid of the wavy cylinder

2.3 计算模型验证

本文首先验证未受控波浪型圆柱计算模型,探究展向高度Lz、无量纲时间步长∆t*、网格参数(波浪型圆柱周向节点数N,第一层边界层高度∆y)对圆柱的平均阻力系数(time-average drag coefficient,Cdmean),脉动升力系数(fluctuating lift coefficient,Clrms)和Strouhal 数(St)的影响,计算结果如表1.可以看出本文的计算结果与仿真数据(num.)[29]基本一致,充分验证了数值方法与网格划分的准确性,综合考虑计算精度与速度,选取Case2 作为其他受控工况下的数值模拟.

表1 Re=3000 下波浪型圆柱的网格独立性验证和周期性边界条件验证Table 1 Grid independence test and the periodic boundary condition validation for the wavy cylinder at Re=3000

为了验证周期性边界条件,取Lz=3λ的波浪型圆柱在相同网格参数和无量纲时间步长∆t*下进行大涡模拟,发现Case8 中Lz=3λ的波浪型圆柱的Cdmean,Clrms和St与Case2 中Lz=2λ的波浪型圆柱基本相同,因此可以看出Case2 中Lz=2λ的波浪型圆柱足以应用于当前模拟,此外,下文将讨论周期性边界条件的其他验证.

受控波浪型圆柱示意图如图3 所示,在波浪型圆柱前后驻点处沿展向狭缝进行定常吹吸气来进行主动控制,吹吸气动量系数(momentum coefficient,Cμ)定义如下

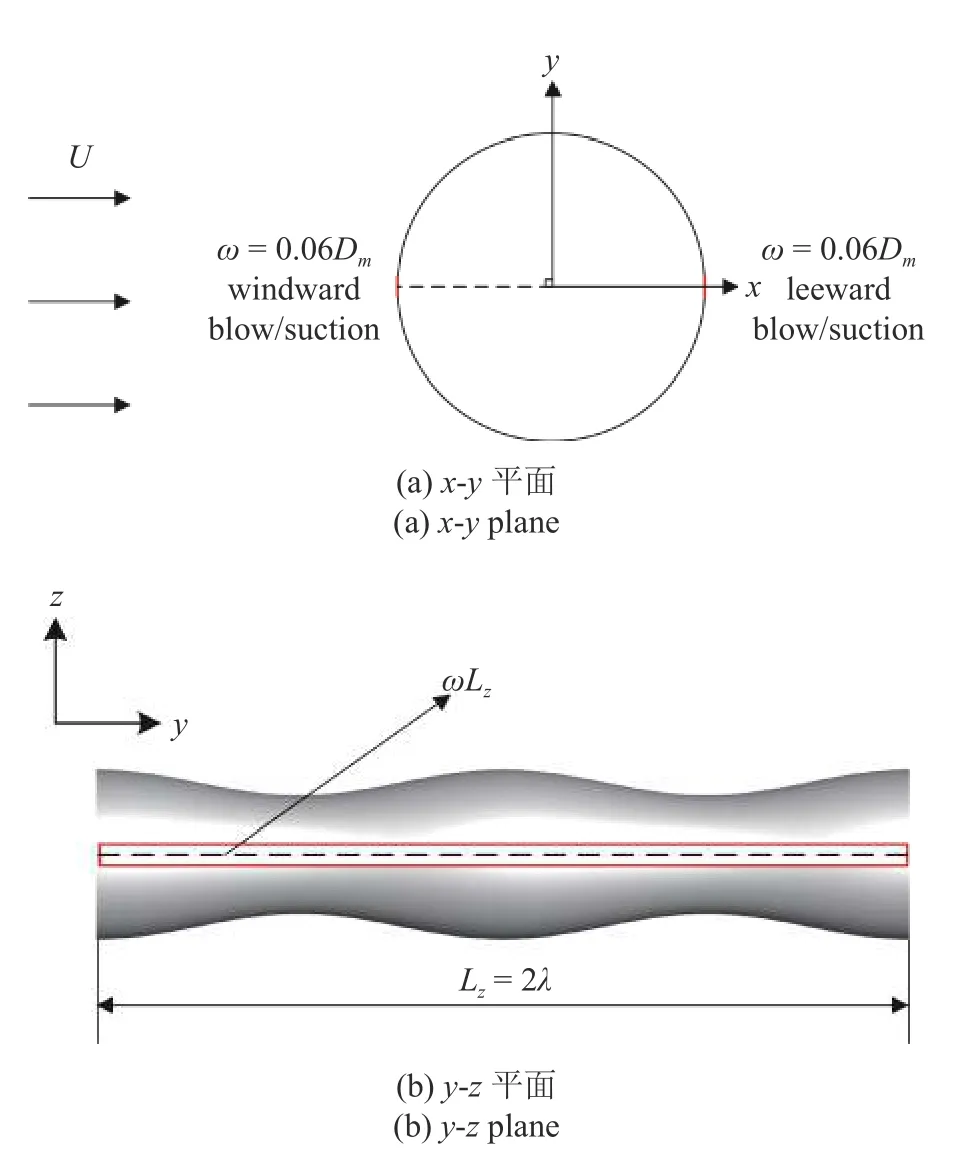
图3 受控波浪型圆柱示意图Fig.3 Schematic of the controlled wavy cylinder

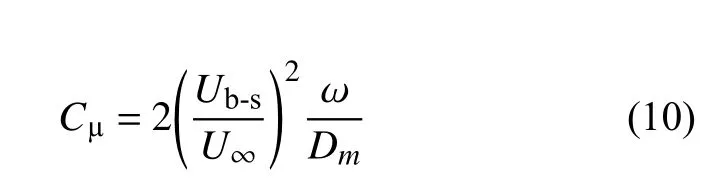
其中,ω为狭缝宽度,Ub-s为吹吸气速度,Choi 等[6]指出为了控制流动的绝对不稳定性通常需要向流场注入与来流速度相当的动量来控制旋涡脱落,本文参考陈文礼等[26]固定狭缝宽度为ω/Dm=0.06,通过改变吹吸气速度来控制动量输入,用大涡模拟分别计算前吹气后吸气和前后吸气两种控制方式在不同吹吸气动量系数(选Ub-s/U∞=0～ 1,增量为0.25,对应Cμ=0,0.007 5,0.03,0.067 5,0.12)的控制效果,定常吹吸气狭缝边界条件采用速度入口(velocityinlet),改变正负值对应吹吸气,计算域以及其他边界条件参照验证中的Case2,网格划分示意图如图4所示.

图4 受控波浪型圆柱网格划分示意图Fig.4 Schematic diagram of grid of the controlled wavy cylinder

3 结果分析

3.1 平均阻力系数和脉动升力系数

图5 显示的是前后吸气和前吹后吸两种方案在Cμ=0～ 0.1 2,共四种吹吸气动量系数下的Cdmean和Clrms,并与未受控的波浪型圆柱和直圆柱(exp.)[30]做对比,为了表述方便,前后吸气流动控制方式用符号SS 表示,前吹气后吸气流动控制方式用符号BS 表示.

从整体上看,受控和未受控波浪型圆柱的Cdmean和Clrms均高于直圆柱,从图5(a)中可以看出,SS 下波浪型圆柱的Cdmean随着Cμ的增加而逐渐上升,当Cμ=0.12 时,Cdmean较未受控波浪型圆柱和直圆柱分别增加约17.8%和21.3%,而BS 下波浪型圆柱的Cdmean随着Cμ的增加整体波动不大,当Cμ=0.007 5 时,Cdmean略低于未受控波浪型圆柱,当Cμ=0.12 时,Cdmean较未受控波浪型圆柱和直圆柱分别增加约3% 和5.9%.从图5(b) 中可以看出,BS 和SS 下随着Cμ的增加均显著提高了波浪型圆柱的脉动升力系数,BS 下随着Cμ的增加波浪型圆柱的Clrms略高于SS,最大较未受控波浪型圆柱分别增加约391%和341%,较直圆柱分别增加约636%和562%.

图5 Cμ=0～ 0.12 下受控波浪型圆柱平均阻力系数和脉动升力系数变化Fig.5 Variation of Cdmean and Clrms of the controlled wavy cylinder with Cμ=0～ 0.12

3.2 表面压力系数

表面压力系数(pressure coefficient,Cp)能够直接反映出波浪型圆柱和受控波浪型圆柱的表面受力情况,为了方便观察表面Cp分布,将波浪型圆柱的表面沿母线剪开,并以角度“θ”和高度“Z/H”作为横、纵坐标铺平,如图6(a)所示,展开后的表面时均压力系数分布如图6(b)所示,为了表述方便,SS0.12代表在Cμ=0.12 下进行前后吸气,BS0.12 代表在Cμ=0.12 下进行前吹气后吸气,其他以此类推.

图6 Cμ=0～ 0.12 下受控波浪型圆柱时均压力系数分布图Fig.6 Distribution diagram of time-average Cp of the controlled wavy cylinder with Cμ=0～ 0.12

从图6 中可以看出整体的Cp分布基本保持对称,BS 下随着Cμ的增加,波浪型圆柱的高压区范围和强度大于0.6的区域)逐渐减小,但低压区小于−0.6的区域)逐渐增大,这可能是BS下波浪型圆柱的平均阻力系数整体波动不大的原因;SS 下随着Cμ的增加,波浪型圆柱的高压区范围和强度较未受控时基本没变化,但低压区逐渐增大,这可能是SS 下波浪型圆柱的平均阻力系数大于未受控波浪型圆柱的原因,此外,BS 下随着Cμ的增加波浪型圆柱的低压区范围变化幅度大于SS.由此可见,在前驻点进行吹气能降低高压区的范围和强度,而吸气则对高压区的影响不大,在后驻点进行吸气能增大低压区的范围和强度.

3.3 旋涡形成长度和最大湍流强度长度

旋涡形成长度(vortex formation length,Lfc)和最大湍流强度长度(maximum turbulence intensity length,Lfu)能够反应波浪型圆柱的流场特性,Lfc定义为尾迹中心线上U/U∞=0 的点到波浪型圆柱中心的距离,Lfu定义为尾迹中心线上μ′/U∞最大值的点到波浪型圆柱中心的距离[31],其中U和μ′分别为波浪型圆柱的时均顺流向速度和脉动顺流向速度.图7 和图8 展示了Re=3000 下SS 和BS 在Cμ=0～ 0.12 下波浪型圆柱展向从Node 截面到Saddle截面的Lfc和Lfu,并与未受控波浪型圆柱作对比.

图7 Cμ=0～ 0.12 下受控波浪型圆柱Node 截面到Saddle 截面的LfcFig.7 Lfc from nodal section to saddle section of the controlled wavy cylinder with Cμ=0～ 0.12

图8 Cμ=0～ 0.12 下受控波浪型圆柱Node 截面到Saddle 截面的LfuFig.8 Lfu from nodal section to saddle section of the controlled wavy cylinder with Cμ=0～ 0.12

从图中可以看出,未受控波浪型圆柱的Lfc从Node 截面到Saddle 截面增加,Lam 等[31]在实验中也观察到类似的结果.SS 和BS 下波浪型圆柱的Lfc和Lfu随着Cμ的增加而减小,并且远小于未受控波浪型圆柱,这表明波浪型圆柱近尾迹存在能量强而集中的旋涡,直接导致脉动升力显著增大,此外,SS 和BS 下波浪型圆柱的Lfu随着Cμ的增加较未受控时趋势发生改变,当Cμ=0.12 时,Lfu的变化趋势呈倒“V”字形,此时波浪型圆柱近尾迹的流动结构可能发生改变.

3.4 环量

环量(circulation,Γ)是涡流动力学中的重要物理量,其表达式为

其中ω代表涡量,无量纲环量Γ*定义为

图9 和图10 分别为Cμ=0～ 0.12 下受控波浪型圆柱Node 截面和Saddle 截面负向涡环量大小,涡旋结构的提取是基于λci准则[32],λci为速度梯度张量复特征值的虚部.由于湍流运动的复杂性,目前尚没有统一的方法来确定涡旋尺度,根据原理目前涡旋尺度的提取方法大致分为两种,第一种是将涡核附近流场与模式涡旋拟合,以拟合涡旋的参数来表征实际涡旋[33],第二种是使用涡量的等值线来代表涡旋的范围[34],由于第一种方法得到的并不是真实的涡旋尺度,本文选取第二种方法.

图9 BS 在Cμ=0～ 0.12 下受控波浪型圆柱Node 截面和Saddle 截面的Γ*变化Fig.9 Evolution of normalized circulation distributions at nodal and saddle sections for the controlled wavy cylinder with Cμ=0～ 0.12 under BS control method

图10 SS 在Cμ=0～ 0.12 下受控波浪型圆柱Node 截面和Saddle 截面的Γ*变化Fig.10 Evolution of normalized circulation distributions at nodal and saddle sections for the controlled wavy cylinder with Cμ=0～ 0.12 under SS control method

从图9 和图10 中可以看出,未受控波浪型圆柱Node 截面和Saddle 截面的无量纲环量Γ*分别在x/Dm=2.68 和x/Dm=2.88 处达到峰值,随着涡旋往下游发展,Γ*开始逐渐减小.BS 和SS 下波浪型圆柱Node 截面和Saddle 截面的近尾迹环量Γ*相比于未受控工况显著增大,且其峰值随着Cμ的增加而增大,这可能是因为通过在波浪型圆柱后驻点进行吸气使得涡旋集中在波浪型圆柱的后部,减缓了涡旋的黏性耗散,使得波浪型圆柱近尾迹涡旋总强度增加,这可能是两种流动控制方式下波浪型圆柱的脉动升力系数显著增加的主要原因,此外,在相同Cμ下,BS 下波浪型圆柱的近尾迹无量纲环量Γ*略大于SS.

3.5 湍动能

图11 给出了Re=3000 下SS 和BS 在Cμ=0～0.12 下的波浪型圆柱在x-y平面的无量纲湍动能云图,并与未受控波浪型圆柱作对比.

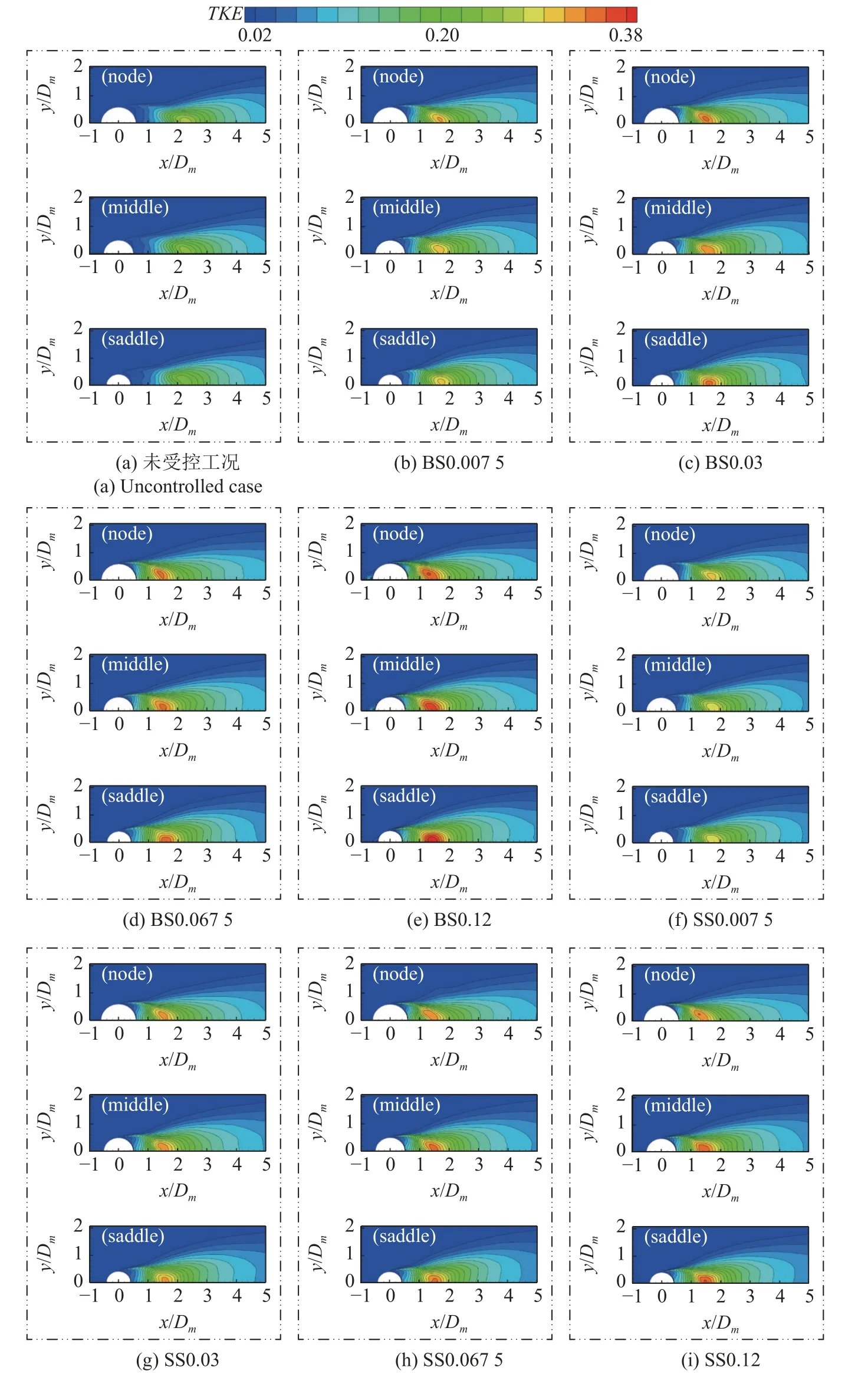
图11 Cμ=0～ 0.12 下x-y 平面波浪型圆柱和受控波浪圆柱在 Node,Middle 和 Saddle 截面的湍动能分布Fig.11 Normalized x-y components turbulent kinetic energy distributions at nodal,middle and saddle sections for the controlled wavy cylinder compared with that of an uncontrolled case in the x-y plane with Cμ=0～ 0.12

无量纲湍动能(normalized turbulent kinetic energy,TKE)定义如下

其中μ′,ν′,ω′分别为x,y,z三个方向的脉动速度分量.

从图中可以看出,与未受控的波浪型圆柱相比,随着Cμ的增加,BS 和SS 下波浪型圆柱各个截面的高TKE区域(〈TKE〉 大于0.26)和TKE最大值显著增加,这一特征与图7 和图8 中Lfc和Lfu的缩短相一致,BS 在每个Cμ下波浪型圆柱各个截面的高TKE区域和TKE最大值要略大于SS.未受控波浪型圆柱Node 截面的高TKE区域和TKE最大值要大于Middle 截面和Saddle 截面,这与Lam 等[29]的研究一致.BS 和SS 下随着Cμ的增加,波浪型圆柱TKE最大值位置开始发生转移,当Cμ=0.12 时,TKE最大值位置出现在Saddle 截面附近,这可能是当Cμ=0.12 时,Lfu的变化趋势呈倒“V”字形的原因,这可以部分归因于驻留在Saddle 截面的顺流向涡流.由此可见,BS 和SS 流动控制方式改变了波浪型圆柱尾流的TKE分布,TKE值显著增大导致尾流场速度脉动显著增加.

图12 给出了y/Dm=0 时,BS 和SS 在Cμ=0.12 下的波浪型圆柱和Lz=2λ,3λ的波浪型圆柱在x-z平面的无量纲TKE云图.从图中可以看出,Lz=2λ,3λ的波浪型圆柱TKE值均沿展向呈现周期性特征,并且局部TKE最大值出现在Node 截面,Lam 等[29]和Zhang 等[35]通过数值模拟和PIV 实验在一系列波浪型圆柱上也观察到这一现象,这表明Lz=2λ的波浪型圆柱足够捕捉到流动特征.此外,从图中可以看出BS0.12 和SS0.12 下波浪型圆柱近尾迹的TKE分布发生改变,局部TKE最大值出现在Saddle 截面附近,这也是x-y平面BS0.12 和SS0.12 下波浪型圆柱Saddle 截面的高TKE区域和TKE最大值大于Node 截面的原因,高TKE区域和TKE最大值较未受控波浪型圆柱显著增加,未受控波浪型圆柱TKE最大值区域大约在x/Dm=2.3 处,SS0.12 和BS0.12 下波浪型圆柱TKE最大值区域的位置分别大约在x/Dm=1.5,x/Dm=1.4 处,相较于未受控时更靠近于波浪型圆柱.

图12 Cμ=0.12 下y/Dm=0 时,x-z 平面波浪型圆柱和受控波浪型圆柱的湍动能分布Fig.12 Normalized x-z components turbulent kinetic energy distributions at y/Dm=0 for the controlled wavy cylinder compared with that of an uncontrolled case in the x-z plane with Cμ=0.12

3.6 三维涡结构

涡的识别方法可以分为三代[36],其中第二代中的Q 准则运用较为广泛,表达式如下

式中,A为对称张量,B为反对称张量,∥ ·∥Fro2为矩阵的Frobenius 范数.

BS0.12 和SS0.12 对波浪型圆柱近尾迹的Γ*有很大影响,使得受控波浪型圆柱的脉动升力系数显著增加,下面通过分析BS0.12 和SS0.12 下波浪型圆柱的流动结构来分析Γ*和TKE显著增加的原因,对BS0.12 和SS0.12 下波浪型圆柱的涡结构采用Q 准则识别,如图13 所示,提供三个视角view1,view2,view3.

从图中可以看出,未受控波浪型圆柱的剪切层分离,由于表面形状的影响在波浪型圆柱的下游处形成“肋状涡”,并且可以观察到周期性的“卡门涡街”现象,BS0.12 和SS0.12 下波浪型圆柱剪切层分离较早,高强度的涡旋向波浪型圆柱后方靠拢,导致近尾迹涡旋总强度显著增加,此外,受控波浪型圆柱的展向涡流从Node 截面向Saddle 截面汇聚,与顺流向涡流相互作用,如图13 中黑色虚线方框所示,这也是y/Dm=0 时x-z平面局部TKE最大值出现在Saddle 截面和x-y平面BS0.12 和SS0.12 下波浪型圆柱Saddle 截面的高TKE区域和TKE最大值大于Middle 截面和Node 截面的原因,涡流的相互作用使得在下游形成的“肋状涡”变大变长,尾迹在横向变宽,产生较大的升力波动,脉动升力系数较未受控波浪型圆柱显著增加,其中当在波浪型圆柱前驻点进行吹气,使得部分剪切层相较于SS0.12 提前分离,分离剪切层与波浪型圆柱下游涡流的耦合作用将产生更大的脉动升力,这可能是 BS0.12 下波浪型圆柱的脉动升力系数大于SS0.12 下波浪型圆柱的原因.

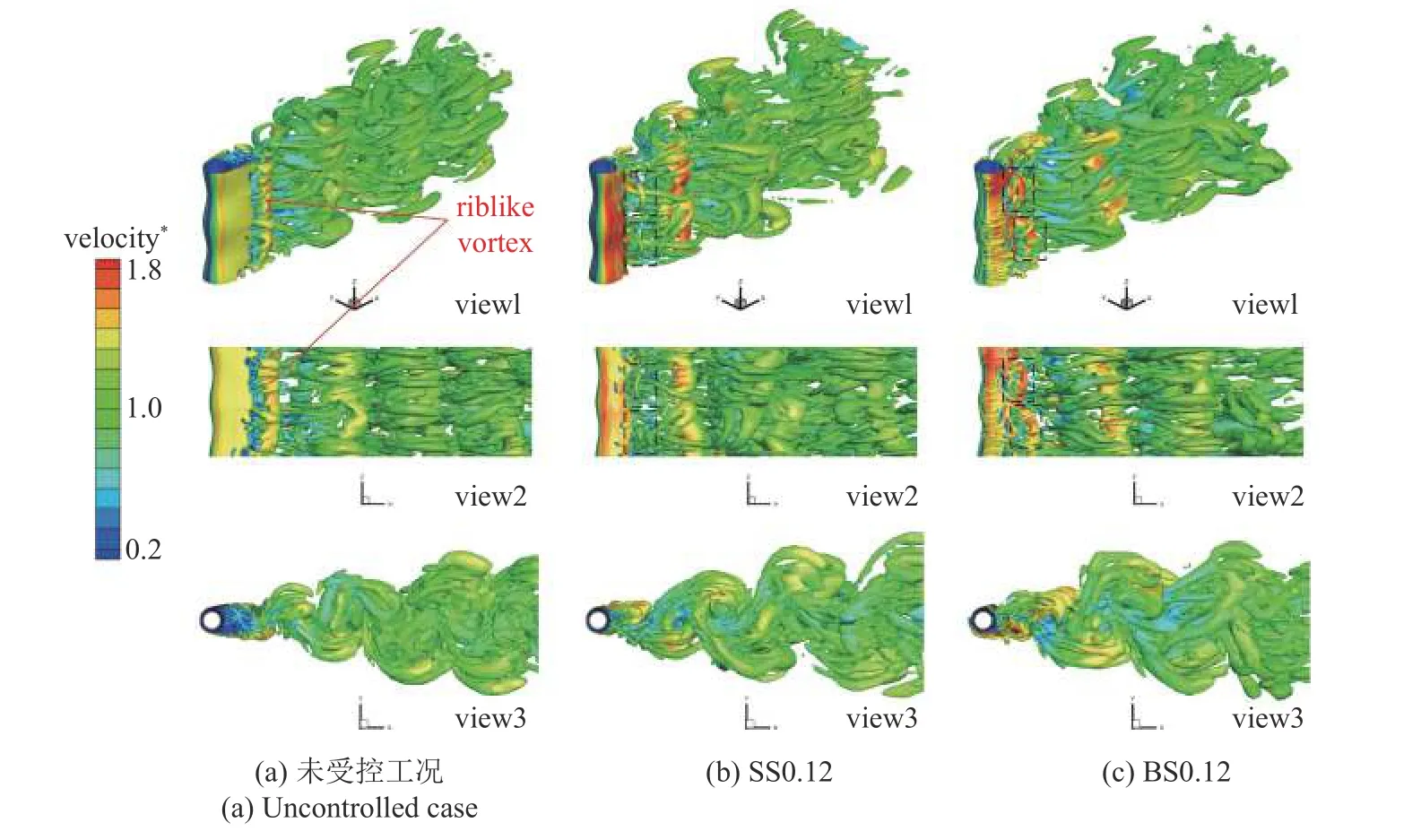
图13 SS0.12 和BS0.12 下波浪型圆柱瞬时涡量图(Q=6000),view1 为整体视图,view2 为前视图,view3 为俯视图Fig.13 Instantaneous vorticity diagram of the wavy cylinder with SS0.12 and BS0.12 (Q=6000).View1 is the general view;view2 is the front view;view3 is the top view

3.7 Z 截面涡量图和时均流线图

为了更好地观察两种控制方式下波浪型圆柱的流动结构,取BS0.12 和SS0.12 下波浪型圆柱Node和Saddle 截面的Z方向瞬时涡量图和时均流线图,并与未受控波浪型圆柱作对比,如图14 和图15 所示.从图中可以看出,BS0.12 下由于在波浪型圆柱的前驻点进行吹气,气流与来流相反,与周围气流发生较强的剪切作用,在波浪型圆柱前部产生一对驻涡,使得波浪型圆柱前部接近流线型,起虚拟气动外形效应,尽管在后驻点进行吸气,但整体的阻力系数变化不大,两种控制方式下波浪型圆柱Node 和Saddle 截面的回流区都显著变短,使得低压中心更接近波浪型圆柱后部,Node 和Saddle 截面下游处尾迹变宽,显著地增加了波浪型圆柱的脉动升力,由于BS0.12 下波浪型圆柱的部分剪切层提前分离,回流区中出现一对驻涡紧贴在波浪型圆柱表面,并且提前分离的剪切层与尾流的耦合作用使得波浪型圆柱下游较SS0.12 出现更多碎涡.

图14 SS0.12 和BS0.12 下波浪型圆柱Node 和Saddle 截面瞬时涡量图Fig.14 Z-vorticity of the wavy cylinder with SS0.12 and BS0.12 at nodal and saddle sections

图15 SS0.12 和BS0.12 下波浪型圆柱Node 和Saddle 截面时均流线图Fig.15 Time-average streamline diagram of the wavy cylinder with SS0.12 and BS0.12 at nodal and saddle sections

4 结论

本文运用大涡模拟在亚临界雷诺数(Re=3000)下采用前吹后吸和前后吸气两种流动控制方式对三维波浪型圆柱进行数值模拟,探究了波浪型圆柱平均阻力系数和脉动升力系数的变化规律,并对波浪型圆柱的时均压力系数、环量、湍动能和近尾迹流动结构进行详细分析,主要结论如下.

(1) BS 下随着Cμ的增加波浪型圆柱的Cdmean较未受控时变化不大,而SS 时则逐渐增大,波浪型圆柱的Cdmean较未受控时最大分别提升约3% 和17.8%,而较直圆柱最大分别提升约5.9%和21.3%;随着Cμ的增加,BS 和SS 下的波浪型圆柱的Clrms显著增大,较未受控时最大分别提升约391% 和341%,而较直圆柱最大分别提升约为636% 和562%.

(2)BS 和SS 改变了波浪型圆柱的表面压力分布,由于在波浪型圆柱前驻点吹气使前端趋于流线型,BS 下随着Cμ的增加波浪型圆柱的高压区减小,在后驻点吸气使得低压区增大,而SS 下波浪型圆柱的高压区基本不变而低压区增大.

(3)两种流动控制方式使波浪型圆柱近尾迹的Lfc和Lfu变短,无量纲环量Γ*增大,从而使得波浪型圆柱的脉动升力系数显著增大,TKE最大值区域较未受控时更靠近波浪型圆柱,局部TKE最大值的位置随着吹吸气动量系数的增加开始转移,在Cμ=0.12 时出现在Saddle 截面附近,Lfu的变化趋势发生转变呈现倒“V”字形.

(4)BS 和SS 在Cμ=0.12 下波浪型圆柱的回流区变短,高强度的涡旋向波浪型圆柱后方靠拢导致近尾迹涡旋总强度增加,展向涡流从Node 截面向Saddle 截面汇聚,与顺流向涡流相互作用在波浪型圆柱下游形成的“肋状涡”变大变长,尾迹在横向变宽,脉动升力显著增加,BS 下波浪型圆柱由于在前驻点吹气导致部分剪切层相较于SS 时提前分离,回流区中出现一对驻涡紧贴波浪型圆柱表面,并且与下游尾涡的耦合作用会产生更大的升力脉动.