一类高效率高分辨率加映射的WENO 格式及其在复杂流动问题数值模拟中的应用

钟 巍 贾雷明 王澍霏 田 宙

* (西北核技术研究所,西安 710024)

† (北京大学数学科学学院,北京 100871)

引言

针对包含激波或精细流场结构的复杂流动问题,往往要求数值模拟方法具备高精度和高分辨率.加权本质无振荡 (weighted essentially non-oscillatory,WENO) 格式[1]在间断附近拥有本质无振荡 (essentially non-oscillatory,ENO) 特性,同时在光滑区域能够获得高阶精度,因此,在复杂流动问题的数值模拟中广受欢迎,并已经在诸多领域得到大量成功应用[2-25].

Liu 等[26]提出了第一个WENO 格式,他们在r阶精度的ENO 格式基础上,通过对其所有候选模板的权系数进行一个凸组合,获得了精度为(r+1)阶的WENO 格式.Jiang 等[1]通过定义新的光滑因子,提出了经典的WENO-JS 格式,该格式在普通光滑区域能够获得(2r− 1)阶收敛精度.

Henrick 等[27]指出,WENO-JS 格式在光滑区域极值点附近会出现收敛精度丢失的问题.通过系统的理论分析,他们给出了WENO 格式的权系数在光滑区域极值点附近获得最佳收敛精度的充分必要条件,并据此构造了一个关于WENO-JS 格式权系数的映射函数使得映射后的权系数满足上述充分必要条件,相应的格式被称为WENO-M.特别地,WENO-M格式在构造映射函数时采用的准则被学者们广泛采用[28-32].然而,由于引入了映射操作,WENO-M 格式的计算效率受到了严重的影响,相对WENO-JS 格式而言,其额外计算时间增加了25%左右[33].不仅如此,Feng 等[28]发现WENO-M 格式的映射函数在权系数为0 的附近会放大不光滑模板的作用,这被认为是造成WENO-M 格式在长时间模拟时出现精度丢失的关键原因.于是,他们新增了一个限制条件,即要求映射函数在0 附近的导数值为0.为此,他们设计了一个分片多项式映射函数,相应的格式被称为WENO-PM6.WENO-PM6 格式具有非常低的数值耗散,因此,其在长时间模拟时仍然能够获得非常高的分辨率,且对于精细流场结构的捕捉能力远远高于WENO-JS 和WENO-M 格式.但是,它引入的分片多项式映射函数带来了更加复杂的数学运算操作,这使得其计算效率比WENO-M 格式还要低.本文后面给出数值算例测试结果表明,WENO-PM6 格式相对WENO-JS 格式的额外计算时间增加了50%以上.

除了前面提到的WENO-M 和WENO-PM6,学者们还提出了许多各种形式的加映射的WENO 格式[29-32].显然,这些加映射的WENO 格式都能够很好的克服WENO-JS 格式在极值点附近计算精度丢失的问题,拥有比WENO-JS 格式更低的耗散从而获得更高的分辨率.无一例外的,这些加映射的WENO格式都存在计算效率下降这个普遍的缺陷.

本文巧妙地设计了一个全新的映射函数,其满足现有映射函数的所有设计要求,但在绝大部分区域仅需要一次简单的赋值运算即可完成映射操作.换句话说,新映射函数不会带来严重的额外计算时间消耗,故而具有非常高的计算效率.此外,相应的加映射的WENO 格式还拥有非常低的数值耗散,因此,与已有加映射的WENO 格式相比,计算分辨率得到极大的提高.

1 问题描述与WENO 格式回顾

1.1 问题描述

无黏、可压缩流动的控制方程为欧拉方程组.三维欧拉方程组为

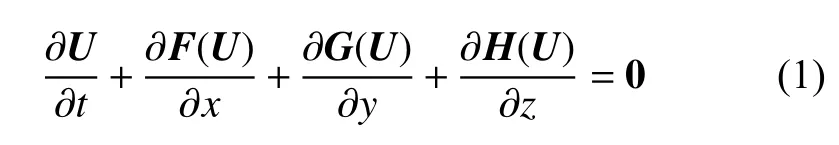
其中

式中,ρ,u,v,w,p,E分别表示流体密度,x,y,z方向的速度分量,压强和单位体积流体的总能量.以下理想气体状态方程与方程(1)组成封闭方程组

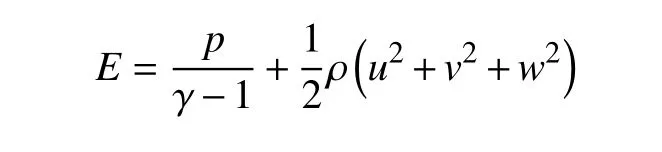
其中,γ 为绝热指数,通常取 γ=1.4.

1.2 WENO 格式回顾

通常情况下,重构都是在特征空间中进行然后将结果投影回物理空间[1].因此,为了方便描述且不失一般性,针对以下一维标量双曲守恒律方程展开讨论

下面简单介绍5 阶WENO-JS、WENO-M 和WENO-PM6 这3 种格式的具体实现方法.

5 阶WENO 重构通过对上述结果做加权平均得到uj+1/2,即

其中,ωk是非线性权系数.

在WENO-JS 格式中,ωk按下式计算

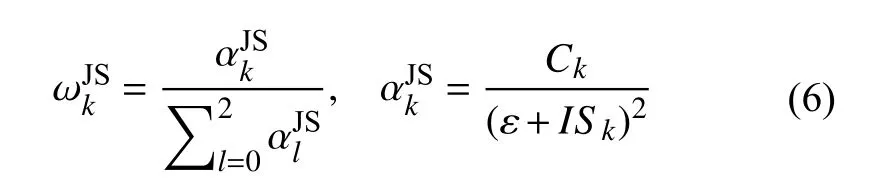
式中,k=0,1,2 (下同),参数 ε 是一个非常小的正数,用来防止分母为0,(C0,C1,C2)=(0.1,0.6,0.3) 是理想权系数,I Sk被称为光滑因子,用来度量子模板的光滑程度,其具体表达式如下

Henrick 等[27]发现WENO-JS 格式在极值点附近无法获得最佳收敛精度,于是他们提出了WENO-M格式,其权系数按下式计算

1.3 时间离散

令

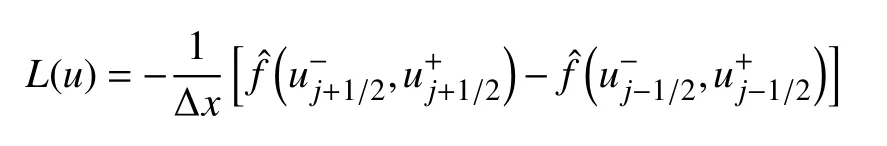
则可以采用合适的时间推进方法求解半离散方程组

本文采用3 阶显式强稳定总变差不增的Runge-Kutta 格式[35-37]进行时间推进,即

2 加近似常值映射的WENO 格式

2.1 新映射函数

先定义标准符号函数的一个光滑近似函数sg(x,µ,T,m),其表达式为

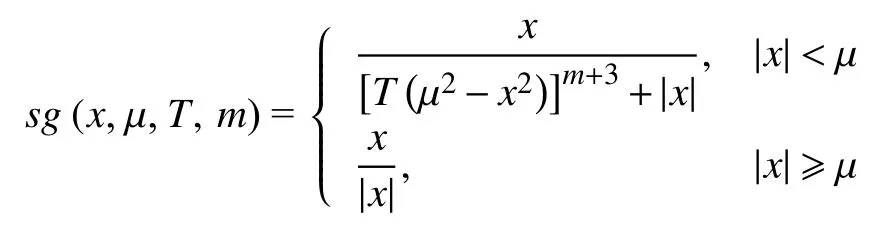
其中,m为正整数,其值越大s g(x,µ,T,m) 越接近实际符号函数;µ 为大于0 的实数且 µ→0 ,其值越小sg(x,µ,T,m)越接近实际符号函数;参数T为用于调整函数形状的一个正实数,其值越小sg(x,µ,T,m) 越接近实际符号函数.在后文中将会看到,sg(x,µ,T,m)越接近实际符号函数对应的格式的计算效率会越高.数学上容易证明,sg(x,µ,T,m) 是一个单调递增的光滑函数.

利用sg(x,µ,T,m) 可以构造一个全局单调递增的映射函数,形式如下

至此,可以定义一个全新的加全局单调递增光滑映射的5 阶WENO 格式,记为WENO-ACM,其权系数按下式计算

作为示例,图1 中分别给出了取m=3,T=30,µk=0.13,ζk=Ck/3和m=2,T=20,µk=10−6,ζk=0.1Ck时,5 阶WENO-ACM 格式对应C k=0.6 的映射函数变化曲线.作为比较,在图中同时给出了WENO-M和WENO-PM6 格式相应的映(射)函数变化曲线.为了方便讨论,不妨称映射结果由0 变为Ck(或由C k变为1)对应的 ω 所在区间为过渡区间.显然,结合图1(a)很容易完成对式(10)中性质的验证.实际上,图1(b)中的WENO-ACM 的映射函数同样满足式(10)中的性质,只是其过渡区间非常小.不过,非常重要的是,通过合理设置参数,在满足光滑性等要求的前提下,尽可能减小过渡区间是非常有必要的.由式(9)可以知道,在过渡区间以外的区间仅进行一次赋值运算,而在过渡区间则要进行复杂的数学运算操作.因此,过渡区间越小,的映射过程所需数学运算操作数也越少,相应的计算效率也会越高.当过渡区间足够小的时候,在绝大部分情况下都只进行一次赋值操作即完成了整个映射过程.因此,可以将看作是一个近似常值映射函数.另外,可以看到,WENO-M 和WENO-PM6 格式的过渡区间都非常大.

图1 WENO-ACM 格式的映射函数曲线Fig.1 Mapping functions of WENO-ACM

2.2 收敛精度分析

对于5 阶WENO-JS 格式,其权系数满足[27]

而在1 阶极值点处,上述关系式进一步退化为

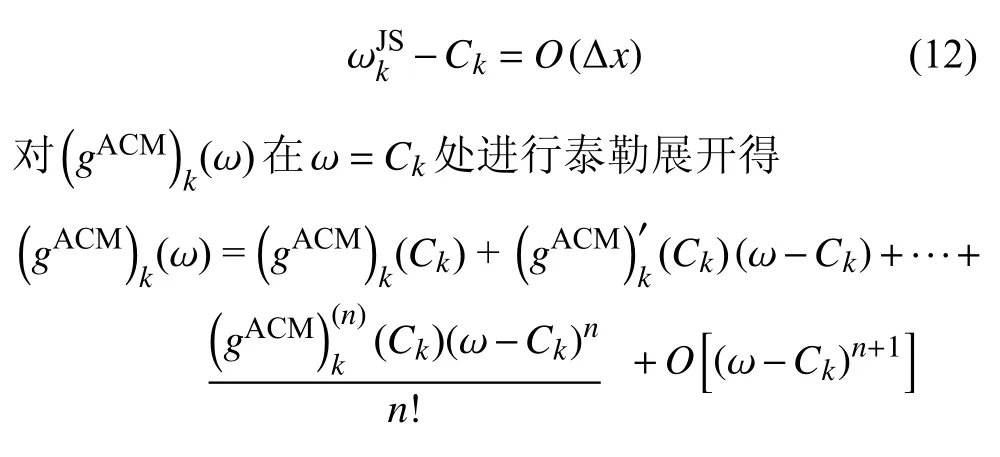
由式(10)可得

2.3 频谱特性分析

利用Pirozzoli[38]提出的近似色散关系(ADR),可以对非线性格式进行频谱特性分析.ADR 分析通过求解模型方程,对给定网格上的全部Fourier 模式进行求解,揭示格式在整个频域的数值表现.对于波数为 φ 的正弦波,从数值结果换算得到的修正波数为 Φ (φ),Φ (φ) 的具体计算方法在文献[38-39]中有非常详细的介绍.Φ (φ) 是一个复数,其实部反映格式的色散性质,虚部则反映格式的耗散性质.

图2 中给出了几种数值格式的ADR 分析结果,其中UW5 是5 阶线性迎风格式,WENO-ACM-(a)和WENO-ACM-(b) 格式的参数分别与图1(a) 和图1(b)中一致.容易看到,WENO-ACM-(a)的色散和耗散性能均明显不如WENO-ACM-(b),也比WENO-M 和WENO-PM6 要差.因此,接下来的内容中本文只对WENO-ACM-(b)进行讨论,且为了简化书写,将用WENO-ACM 表示WENO-ACM-(b).由图2(a)可见,在中波数区间,WENO-ACM 格式相比WENO-JS,WENO-M 和WENO-PM6 格式的色散是有所降低的,但在波数大于2.3 以上的高波数区间,WENO-ACM 格式的色散性能得到了提升.这里重点关注格式的耗散性质,如图2(b)所示,在中波数范围内,WENO-ACM 格式的耗散性质与WENO-M和WENO-PM6 格式非常接近,且均优于WENO-JS格式,而在波数较大的区间,WENO-ACM 格式相对其他格式则表现出了更好的耗散性能.

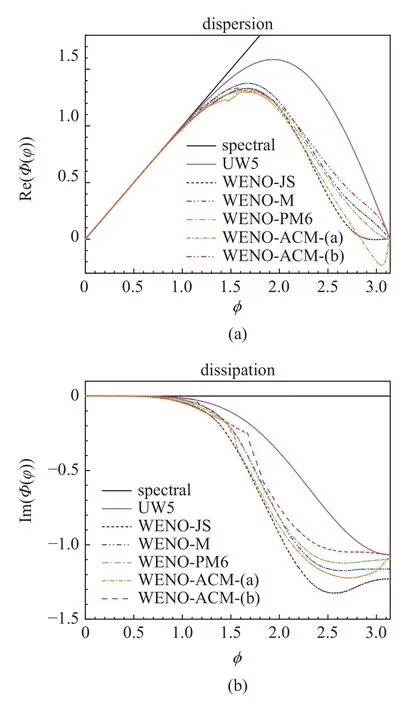
图2 不同WENO 格式的频谱特性曲线比较Fig.2 Comparison of the spectral properties of different WENO schemes

上述ADR 分析结果表明,WENO-ACM 格式是一种低耗散的数值格式.在接下来的一节中,将通过大量的数值算例来证实这一点.

3 数值算例与结果分析

本节通过丰富的数值算例进一步表明本文所提出的新格式在计算效率和低耗散性方面显著的优势.为了更好的比较,将同时给出WENO-JS,WENO-M,WENO-PM6 这3 种非常有代表性格式的计算结果.

在经过大量的数值实验后,本文发现选取如图1(b)中所示参数的时候,WENO-ACM 格式的数值表现是最好的.因此,接下来的部分,WENOACM 格式均指采用如图1(b)中所示参数的情况.同时,根据数值经验,本文建议在实际使用WENOACM 格式时选取这组参数,即在选择参数时确保映射函数的过渡区尽可能小且理想权区间尽量大.

3.1 精度测试

利用一维线性对流方程

进行精度测试.采用周期边界条件,输出时间为t=2.分别考虑下面两种不同的初始条件

为了确保时间收敛精度与空间收敛精度一致,取CFL 数为 ∆x2/3.利用特征线法,容易求得上述两种初始条件下问题的精确解分别为

于是,可得数值格式的L2和L∞误差分别为

表1 给出了不同格式对初始条件1 的L2和L∞误差及其收敛精度.由表1 可知,所有格式均能够获得最佳收敛精度.整体上,WENO-M,WENOPM6 和WENO-ACM 的绝对计算误差是相当的,且要明显小于WENO-JS.不同格式对初始条件2 的L2和L∞误差及其收敛精度计算结果如表2 所示.可以看到,WENO-JS 的L∞收敛精度只有3 阶左右,其L2收敛精度为下降到4 阶以下,而WENO-M,WENOPM6 和WENO-ACM 则仍然能够获得最佳收敛精度,且它们的绝对计算误差明显高于WENO-JS 格式.

表1 不同WENO 格式的 L2 和 L ∞ 误差及其收敛精度 (初始条件1)Table 1 L 2 and L ∞ errors and the convergence properties of various schemes for initial condition 1

表2 不同WENO 格式的 L2 和 L ∞ 误差及其收敛精度 (初始条件2)Table 2 L 2 and L ∞ errors and the convergence properties of various schemes for initial condition 2

为了表明WENO-ACM 格式在计算效率方面的优势,图3 和图4 分别给出了不同格式针对初始条件1 和初始条件2 时的L2和L∞计算误差与CPU 计算时间关系曲线.由图可见,在获得相同计算精度的情况下,WENO-ACM 所消耗的CPU 计算时间是最小的,这表明WENO-ACM 的计算效率是最高的.另外,可以发现,在获得相同的计算精度时,WENOPM6 的CPU 计算时间要大于WENO-M,这表明WENO-PM6 的映射操作带来的额外计算时间要高于WENO-M,从而导致其计算效率出现了严重的下降.在本文最后一小节通过二维数值算例专门讨论上述格式的计算效率问题时,将会再次证实这一结论.

图3 不同WENO 格式对初始条件1 的计算误差与CPU 计算时间关系曲线Fig.3 Comparison of various WENO schemes for initial condition 1 in CPU time and numerical computing errors

图4 不同WENO 格式对初始条件2 的计算误差与CPU 计算时间关系曲线Fig.4 Comparison of various WENO schemes for initial condition 2 in CPU time and numerical computing errors

3.2 长时间模拟测试

为了验证WENO-ACM 格式长时间计算时在稳定性和低耗散性方面的优势,选取一维线性对流方程进行测试.采用周期边界条件,初始条件如下

取输出时间为t=1200,CFL 数为 ∆x2/3.利用特征线法,容易求得问题的精确解为

图5 给出了300 个均匀网格下不同WENO 格式的计算结果.由图可见,WENO-JS 和WENO-M 均出现了非常严重的分辨率下降,这是由于它们的数值耗散太大引起的.WENO-ACM 和WENO-PM6 则在长时间模拟时仍然能够获得非常高的分辨率,这表明它们的数值耗散非常小.此外,图6 给出了不同WENO 格式对该问题的L2和L∞计算误差与CPU计算时间关系曲线.图中结果表明,在获得相同计算精度的情况下,WENO-ACM 所消耗的CPU 计算时间是最少的,这表明其计算效率是最高的.可以看到,WENO-PM6 虽然计算精度高,但其消耗的CPU 计算时间非常大,导致其计算效率甚至比WENO-M还低.

图5 不同WENO 格式对包含高阶临界点光滑问题的长时间模拟结果,N=300, t=1200Fig.5 Results of various WENO schemes for the smooth problem with high-order critical points at long output time,N=300, t=1200

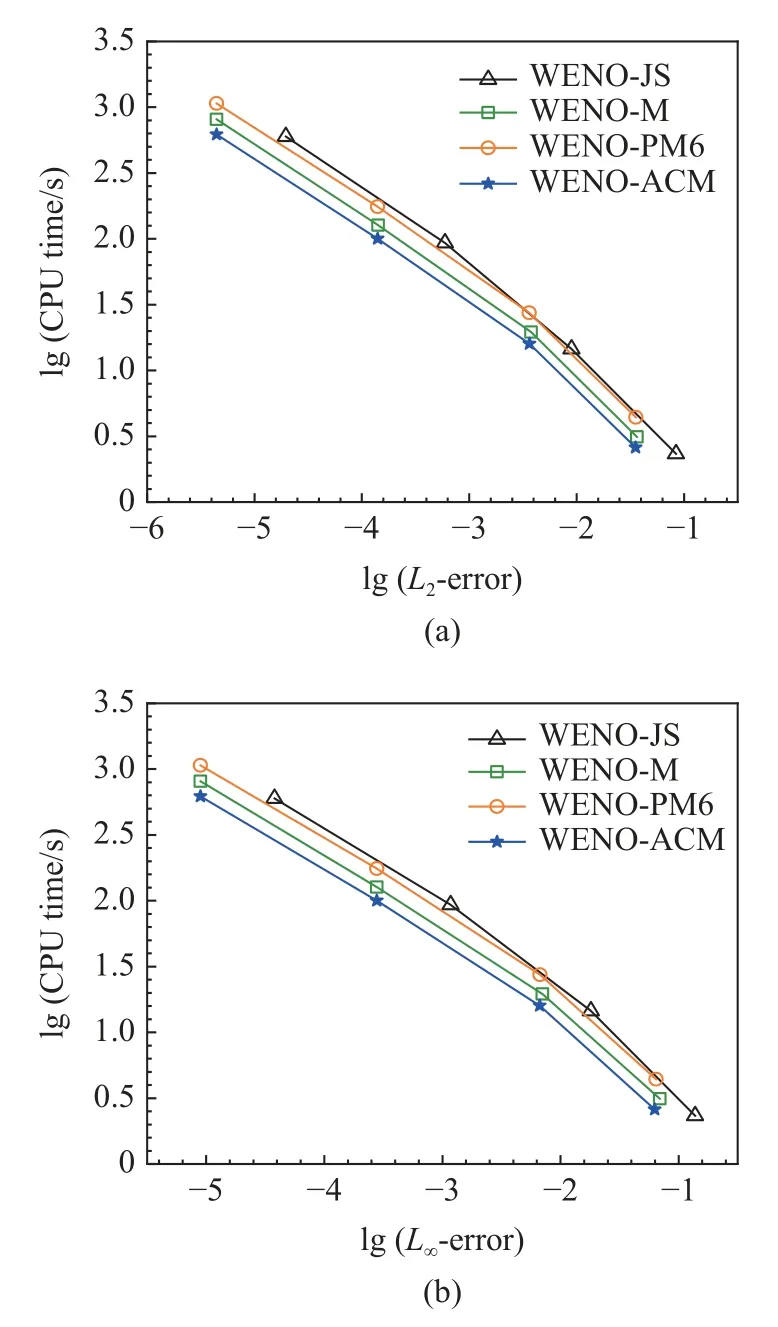
图6 不同WENO 格式对高阶临界点光滑问题的计算误差与CPU 计算时间关系曲线Fig.6 Comparison of various WENO schemes for the smooth problem with high-order critical points in CPU time and numerical computing errors

3.3 一维欧拉方程组

本节对一维欧拉方程组进行模拟,方程组的具体表达形式由式(1)和式(2)很容易得到.在进行有限体积框架下WENO 重构的时候,采用局部特征分解技术,具体实现过程可以参考文献[1,40].所有算例,CFL 数均取0.5,初始条件为U0=(ρ,u,p)(x,0).

3.3.1 激波管问题

先考虑两个标准的激波管问题,即Sod 和Lax激波管问题,其初始条件如下

采用透射边界条件,取200 个均匀网格进行模拟,图7 给出了WENO-JS,WENO-M,WENOPM6 和WENO-ACM 格式将Sod 和Lax 激波管问题分别计算到t=0.25 和t=1.3 的结果(密度).由图可见,WENO-ACM 和WENO-M,WENO-PM6 均给出了比WENO-JS 更高的分辨率.更仔细的观察可以发现,WENO-ACM 的模拟效果要轻微地优于WENO-M 和WENO-PM6,这表明WENO-ACM 的数值耗散是最小的.

图7 不同WENO 格式对Sod 和Lax 激波管问题的模拟结果Fig.7 Results of various WENO schemes for the Sod and Lax shocktube problems

3.3.2 爆炸波碰撞问题

计算由Woodward 等[43]提出的一维爆炸波碰撞问题,其初始条件如下

采用反射边界条件,取400 个均匀网格进行模拟,图8 给出了WENO-JS,WENO-M,WENOPM6 和WENO-ACM 格式将该问题计算到t=0.038的结果(密度),其中参考解是取10 000 个网格时WENO-JS 的计算结果.由图可见,WENO-JS 的分辨率明显低于其他几种格式,而WENO-ACM 的分辨率则是所有格式中最高的,虽然只是轻微的好于WENO-M 和WENO-PM6 格式.同样地,上述结果证明WENO-ACM 具有非常低的数值耗散.

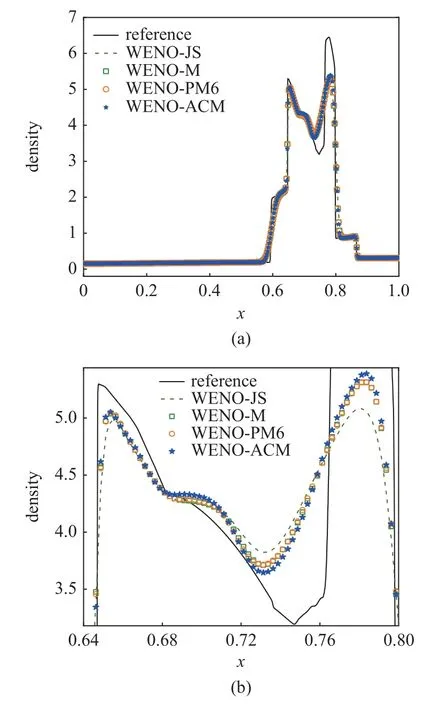
图8 不同WENO 格式对Woodward-Colella 爆炸波碰撞问题的模拟结果Fig.8 Results of various WENO schemes for the Woodward-Colella blast wave interacting problem

3.3.3 激波−熵波相互作用问题

这里模拟两个经典的激波与熵波相互作用问题,其初始条件如下

采用透射边界条件,分别取300 和1500 个均匀网格进行模拟,图9 和图10 依次给出了WENO-JS,WENO-M,WENO-PM6 和WENO-ACM 格式将Shu-Osher 和Titarev-Toro 激波−熵波相互作用问题分别计算到t=1.8 和t=5.0 的结果(密度),其中参考解是取10 000 个网格时WENO-JS 的计算结果.由图9(b)可见,在高频光滑波区域,由于数值耗散太大,WENO-JS 的分辨率是最低的,而得益于低耗散的优点,WENO-ACM 的分辨率是最高的,尽管此时其分辨率只是略微的高于WENO-M 和WENOPM6.然而,由图10(b) 可见,当面对更为苛刻的Titarev-Toro 问题时,WENO-ACM 的分辨率要显著的高于所有其他格式.此时,WENO-JS 的分辨率仍然是最低的,而WENO-PM6 的分辨率也要明显的高于WENO-M.

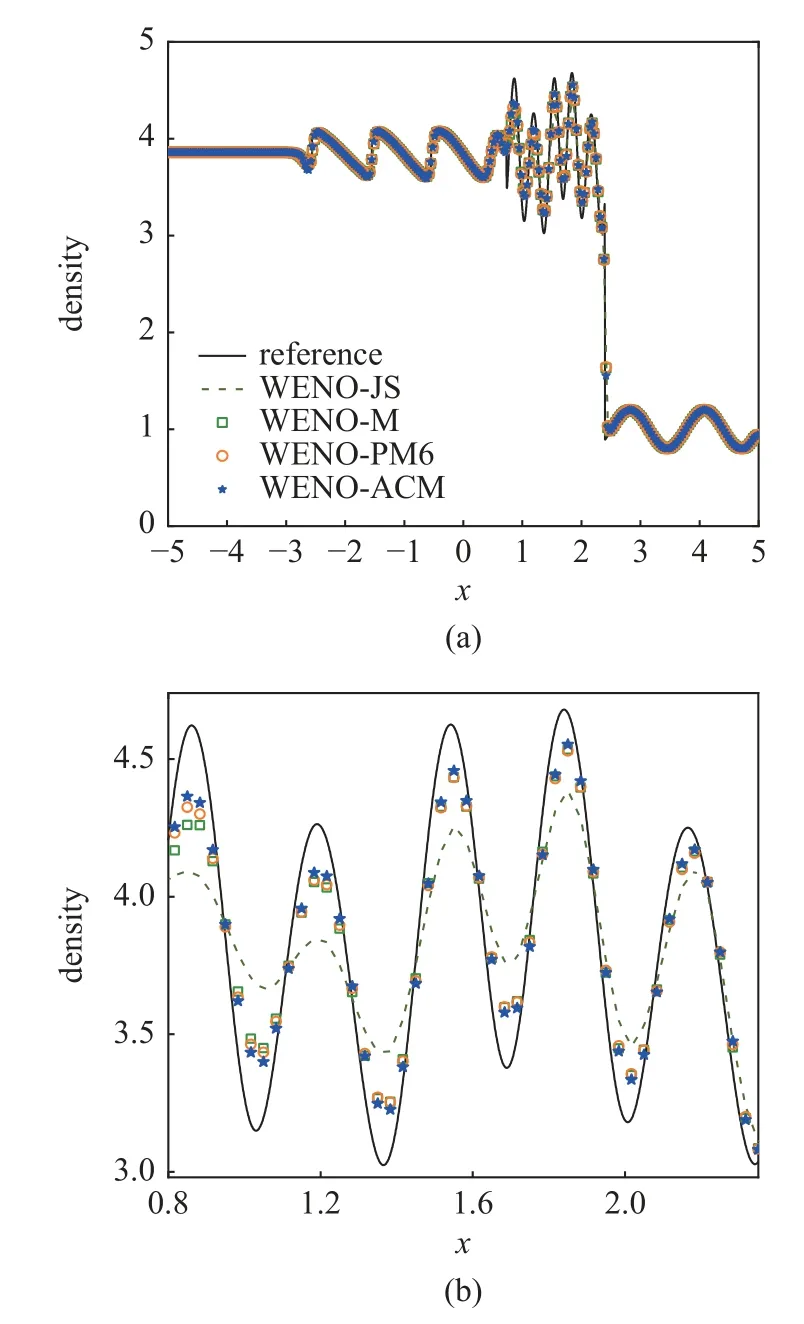
图9 不同WENO 格式对Shu-Osher 激波-熵波相互作用问题的模拟结果Fig.9 Results of various WENO schemes for the Shu-Osher shockentropy interaction problem

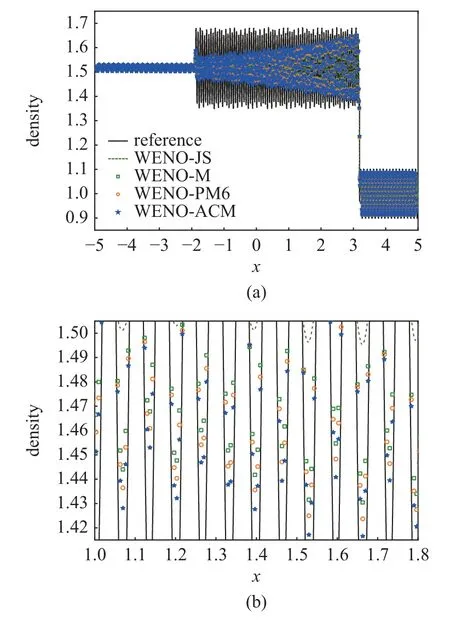
图10 不同WENO 格式对Titarev-Toro 激波-熵波相互作用问题的模拟结果Fig.10 Results of various WENO schemes for the Titarev-Toro shockentropy interaction problem

3.4 二维欧拉方程组

接下来,对二维欧拉方程组进行模拟.同样的,方程组的具体表达形式由式(1)和式(2)很容易得到.仍然在有限体积框架下进行求解,逐维进行WENO 重构,并采用局部特征分解技术.对所有算例,CFL 数均取0.5,在没有特别说明的情况下,绝热指数取 γ=1.4,初始条件为U0=(ρ,u,v,p)(x,y,0).

3.4.1 二维黎曼问题

首先模拟非常经典的二维黎曼问题[48-50],其计算区域为[0,1] × [0,1].已有研究表明,二维黎曼问题有很多不同的解结构[49],这里选取其中一种结构进行模拟,其初始条件如下

4 条边界均取透射边界条件,使用400 × 400 个均匀网格,输出时间为t=0.8.

图11 中给出了WENO-JS,WENO-M,WENOPM6 和WENO-ACM 计算得到的密度等值线图.由图可见,WENO-JS 的分辨率最低,其次是WENO-M.WENO-PM6 的分辨率要略高于WENO-M,但要明显低于WENO-ACM.这表明,WENO-ACM 的数值耗散在所有格式中是最小的.

图11 不同WENO 格式对二维黎曼问题的模拟结果Fig.11 Results of various WENO schemes for the 2D Riemann problem

同时,还可以观察到,WENO-M,WENOPM6 和WENO-ACM 均出现了比较明显的数值振荡——如图中粉色虚线框标注所示.分析原因如下(为方便描述,称映射函数在 ωk=Ck附近用理想权系数代替原权系数对应的 ωk所在的区间为理想权区间): 文献[51]中已经指出,更大的理想权区间是获得更高分辨率的关键,但增大理想权区间同时也提高了放大非光滑子模板上权系数的风险进行导致产生数值振荡.由图1(b)容易发现,这里所考虑的格式的理想权区间大小满足关系: WENO-ACM >WENO-PM6 >WENO-M >WENO-JS,而图11 中数值分辨率高低以及数值振荡的大小同样满足上述关系.显然,这与文献[51]的结论是一致的.尽管如此,这些数值振荡并未影响流场主要波系结构的捕捉,因此,当以追求高分辨率为主要目标时,它们是可以容忍的.这种情况在后面的算例(特别是前台阶流动算例)中同样非常显著,为了节省篇幅,后文中将不再对此进行赘述.

3.4.2 双马赫反射问题

双马赫反射问题[43]被广泛用于测试高分辨率格式的性能.该问题的计算区域为[0,4] × [0,1],初始时刻计算区域的流场分布如下

其中,x0=1/6.在左侧入口处采用入流边界条件,流场状态与初始条件一致,在右侧出口处采用出流边界条件.在底部 [ 0,x0] 区域采用初始条件,[x0,4] 区域采用反射边界条件.在顶部,其边界条件设定如下

图12 中给出了WENO-JS,WENO-M,WENO-PM6和WENO-ACM 计算得到的密度等值线图,其中粉色盒子标注的滑移线附近的不稳定涡结构及主激波后方的伴随结构通常用来衡量数值格式的耗散性能.由图可见,所有格式均能够很好的捕捉到主激波后方的伴随结构.WENO-JS 对滑移线附近的不稳定结构捕捉效果最差,因此其数值耗散最大,然后是WENO-M.WENO-PM6 和WENO-ACM 对滑移线附近不稳定结构的捕捉效果相差不大,均明显优于WENO-JS 和WENO-M.显然,本算例表明WENO-ACM具有非常低的数值耗散.

3.4.3 前台阶流动问题

前台阶流动问题[43]在高分辨率格式的数值测试中同样很受欢迎,特别是对发源于马赫杆处的物理不稳定现象即漩涡面卷曲现象的捕捉,对数值格式的低耗散性能提出了非常高的要求[13,52-55].该问题的计算区域为 Ω=[0,0.6]×[0,1]∪[0.6,3]×[0.2,1],即在一个长为3、高为1 的小型风洞内距离风洞左侧入口0.6 的位置放置一个长为2.4、高为0.2 的台阶.整个计算区域在初始时刻的流场状态如下

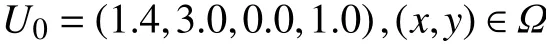
在风洞的左侧入口、右侧出口处分别采用入流边界条件、出流边界条件,在风洞及台阶的壁面都采用反射边界条件,计算输出时间为t=4.0.

图13 和图14 分别给出了网格数取900 ×300 和1800 × 600 时,WENO-JS,WENO-M,WENOPM6 和WENO-ACM 计算得到的密度等值线图.首先,对于上述两种不同网格尺寸,所有格式均能够很好的捕捉到主要的波系结构.由图13 可见,网格数取900 × 300 时,只有WENO-ACM 能够模拟出发源于马赫杆处的漩涡面卷曲现象.当将网格加密到1800 × 600 时,所有格式均能够模拟出上述漩涡面卷曲现象,但WENO-JS 的模拟结果最不显著.WENO-M 和WENO-PM6 都能够观察到非常清晰的漩涡面卷曲结构,但从尺寸上看,WENO-ACM 的模拟效果是最佳的.本算例非常有力的证明了WENOACM 在低数值耗散方面的优势.

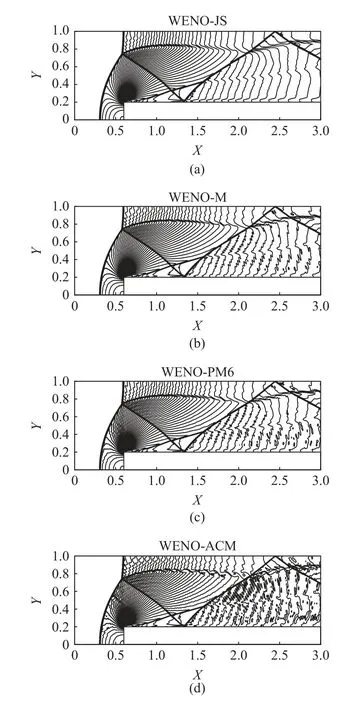
图13 不同WENO 格式对前台阶流问题的模拟结果,900 × 300个网格Fig.13 Results of various WENO schemes for the forward facing step problem,900 × 300 cells

图14 不同WENO 格式对前台阶流问题的模拟结果,1800 × 600个网格Fig.14 Results of various WENO schemes for the forward facing step problem,1800 × 600 cells

3.4.4 瑞利−泰勒不稳定性问题

本算例刻画初始流场中两种不同密度的流体在重力作用下上方密度较大的流体加速进入下方密度较小的流体流动不稳定性现象[56].计算区域为[0,0.25] × [0,1],初始时刻计算区域的流场分布如下

左、右侧均取反射边界条件,上、下则采用常值边界条件,即

需要注意的是,该问题的绝热指数取为 γ=5/3,且在二维欧拉方程组的右侧要添加源项S=(0,0,ρ,ρv)T来体现重力的影响.

图15 给出了网格数取240 × 960 时,WENO-JS,WENO-M,WENO-PM6 和WENO-ACM 对该问题模拟到t=1.95 时的密度等值线图.可以非常清晰的观察到,WENO-ACM 的分辨率要显著的高于其他几种格式,它能够识别出最为丰富的涡结构,这表明它的数值耗散是最小的.而数值耗散最大的WENOJS 模拟结果的分辨率是最低的,随后是WENO-M.WENO-PM6 虽然分辨率要高于WENO-JS 和WENO-M,但仍远远低于WENO-ACM.

图15 不同WENO 格式对瑞利-泰勒不稳定性问题的模拟结果Fig.15 Results of various WENO schemes for the Rayleigh-Taylor instability

3.4.5 开尔文−亥姆霍兹不稳定性问题

最后,对开尔文−亥姆霍兹不稳定性问题[57-60]进行模拟.该问题的计算区域为[0,1] × [0,1],初始时刻计算区域的流场分布如下

其中

四周均取透射边界条件,输出时间为t=0.8.

图16 给出了网格数取512 × 512 时,WENO-JS,WENO-M,WENO-PM6 和WENO-ACM 模拟得到的密度等值线图.由图可见,WENO-JS 模拟得到的涡的尺寸是最小的,其次是WENO-M.WENOPM6 模拟得到的涡的尺寸要明显大于WENO-M,但仔细观察发现要略微的小于WENO-ACM.

图16 不同WENO 格式对开尔文-亥姆霍兹不稳定性问题的模拟结果Fig.16 Results of various WENO schemes for the Kelvin-Helmholtz instability

3.5 计算效率测试

前面的算例已经充分证明WENO-ACM 在低耗散性上与其他几种WENO 格式相比有着显著的优势.现在,仍然利用上一小节的算例,对WENOACM 的计算效率进行专门测试.为了更好的比较,这里对WENO-JS,WENO-M 和WENO-PM6 也进行效率测试.测试时的基本计算条件与上一小节一致,但新增了一组网格条件.测试程序采用 C++代码编写,并在个人计算机上运行,计算机CPU 为 Intel(R)Core(TM)i9-9880 H.为了尽量排除其他因素的影响,测试时仅考虑单个Runge-Kutta 迭代步的CPU 时间消耗.同时,为了消除随机性的影响,每次测试均在相同条件下重复了3 次.

表3～表7 给出了效率测试的结果,其中第一至四行给出了每个Runge-Kutta 迭代步的CPU 时间消耗,并在括号内给出了相对WENO-JS 的额外时间消耗.同时,为了更好的比较,在每个表格的最后两行还以百分比的形式分别给出了WENO-ACM 相对WENO-M 和WENO-PM6 的“额外计算时间消耗减少量”.由表可见: WENO-M 和WENO-PM6 相对WENO-JS 的额外时间消耗分别大于 24%和54%,而WENO-ACM 相对WENO-JS 的额外时间消耗则不超过5%;WENO-ACM 相对于WENO-M 和WENO-PM6的“额外计算消耗减少量”分别大于80%和90%−远远高于WENO-PDM[61]相对WENO-M 的52%的“额外计算消耗减少量”.这表明,WENO-ACM 能够极大的提高加映射的WENO格式的计算效率.

表3 每个Runge-Kutta 步的CPU 计算时间(s)及相对WENO-JS 的额外计算时间(二维黎曼问题)Table 3 CPU time (s) and the extra computational cost per Runge-Kutta step for the 2D Riemann problem

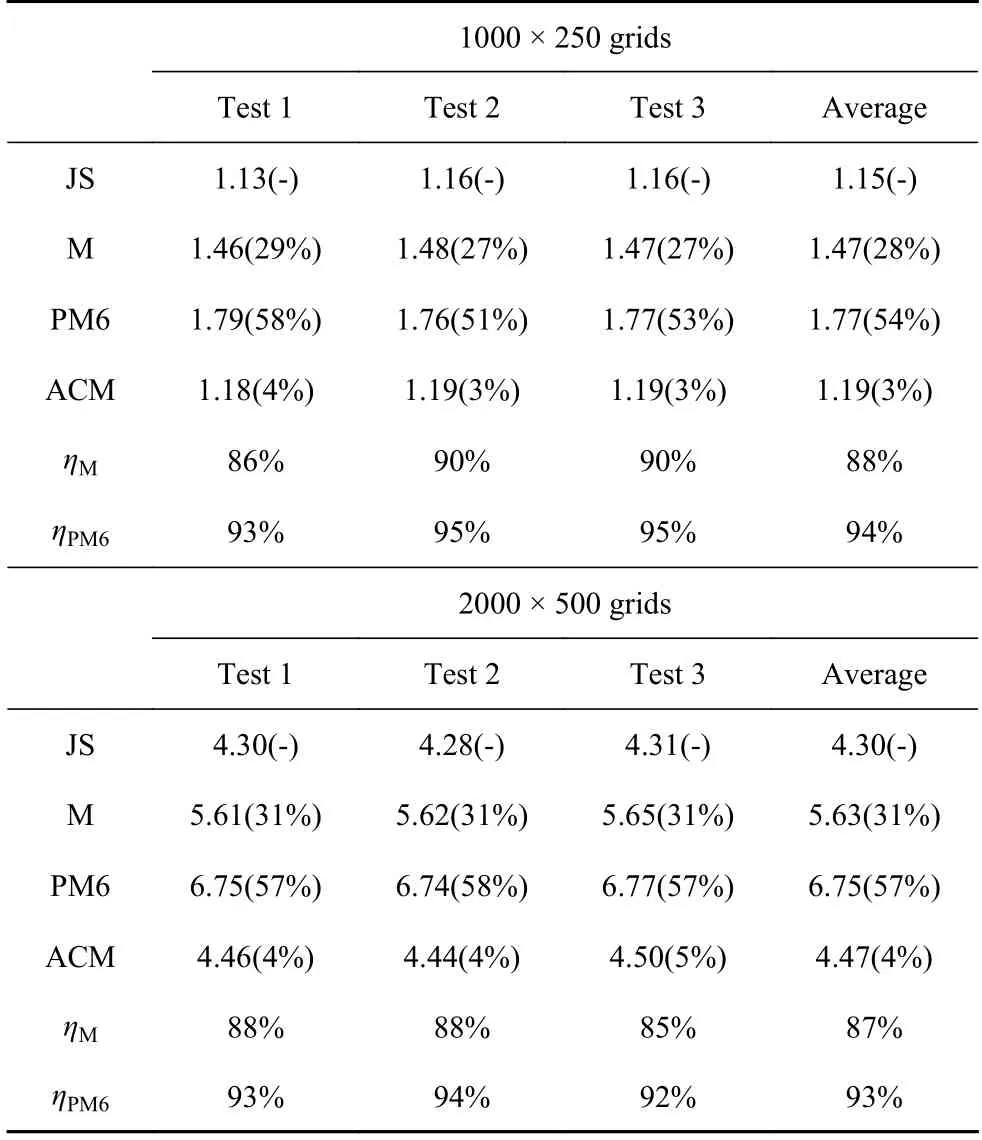
表4 每个Runge-Kutta 步的CPU 计算时间(s)及相对WENO-JS 的额外计算时间(双马赫反射问题)Table 4 CPU time (s) and the extra computational cost per Runge-Kutta step for the double Mach reflection problem

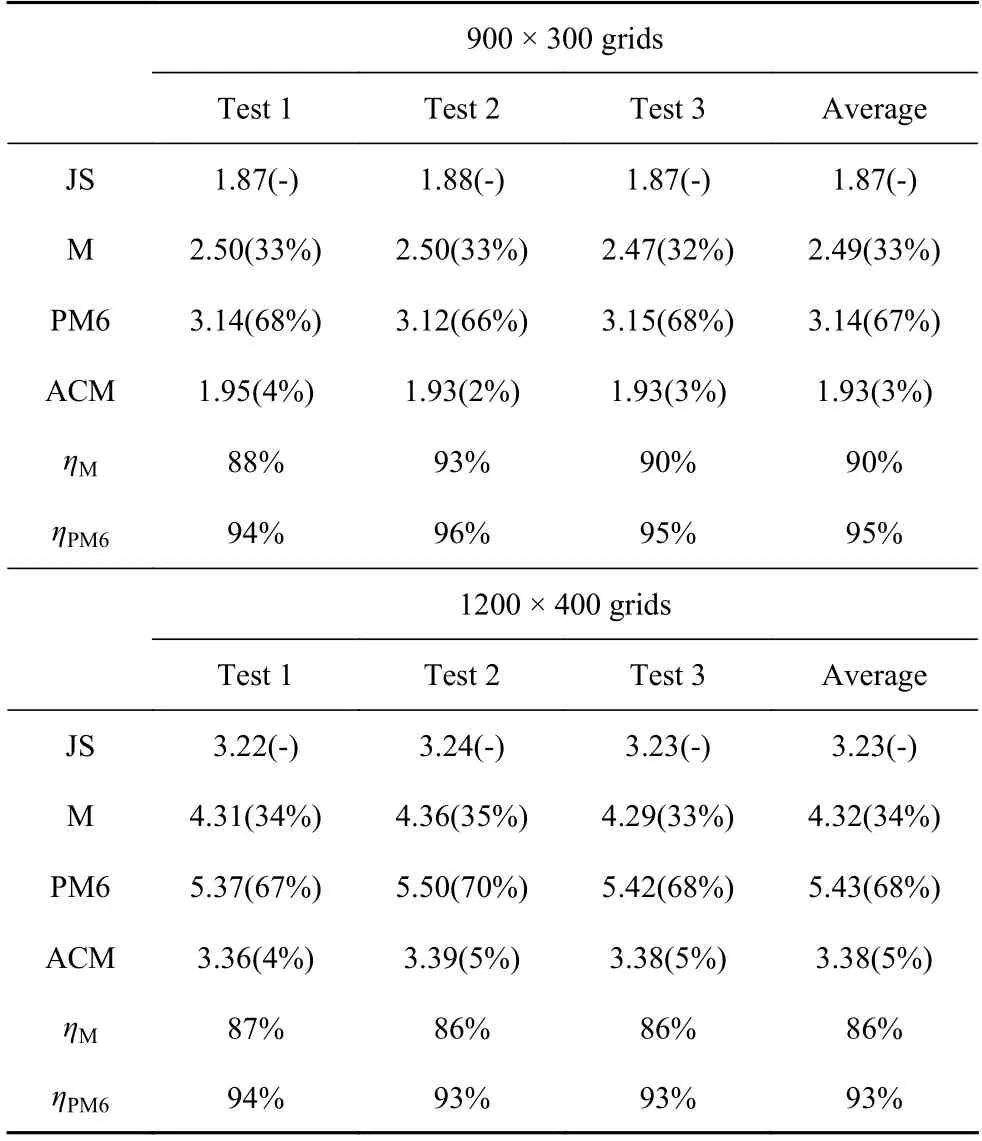
表5 每个Runge-Kutta 步的CPU 计算时间(s)及相对WENO-JS 的额外计算时间(前台阶流问题)Table 5 CPU time (s) and the extra computational cost per Runge-Kutta step for the forward facing step problem

表6 每个Runge-Kutta 步的CPU 计算时间(s)及相对WENO-JS 的额外计算时间(瑞利-泰勒不稳定性问题)Table 6 CPU time (s) and the extra computational cost per Runge-Kutta step for the Rayleigh-Taylor instability

为了获得更清晰的计算时间消耗分布,这里进一步详细统计程序计算所有各部分的CPU 时间,即分别统计特征分解以及特征空间与物理空间来回投影部分(Tch)、重构部分(Trec)、映射部分(Tmap)、其他部分(Toth)的CPU 时间.为了节省篇幅但又不失一般性,以400 × 400 网格的二维黎曼问题和1000 ×250 网格的双马赫反射问题为例,表8 和表9 中分别给出了一个Runge-Kutta 迭代步中不同格式上述各部分CPU 时间的统计结果,并在括号中给出了各部分CPU 时间所占百分比.

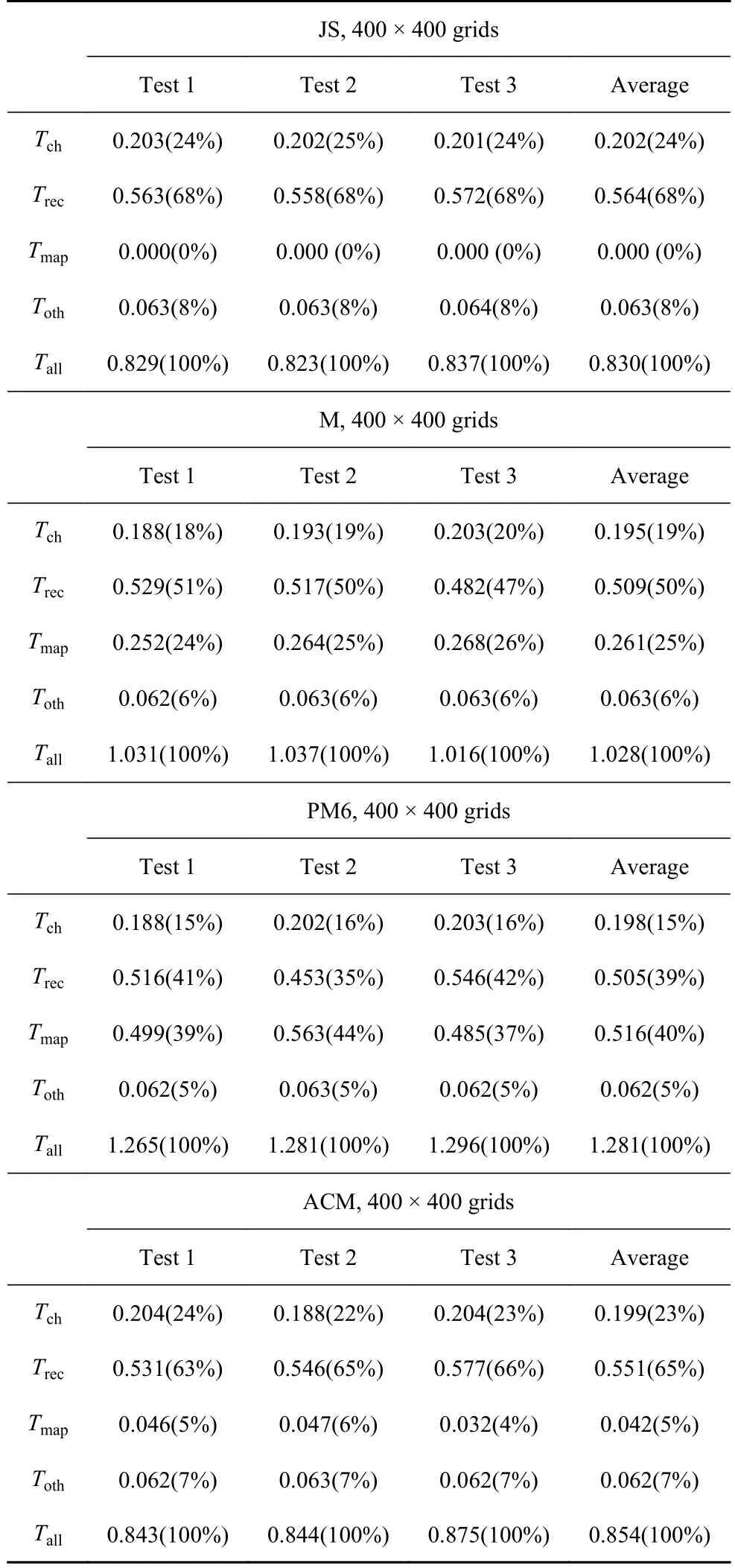
表8 每个Runge-Kutta 步的CPU 计算时间(s)分布情况(二维黎曼问题)Table 8 CPU time (s) allocation per Runge-Kutta step for the 2D Riemann problem

表9 每个Runge-Kutta 步的CPU 计算时间(s)分布情况(双马赫反射问题)Table 9 CPU time (s) allocation per Runge-Kutta step for the double Mach reflection problem

由表可见: 显然,重构部分消耗的CPU 时间占比是最大的;WENO-M 的映射消耗时间(Tmap) 在25%以上,而WENO-PM6 则在40%以上且与重构部分消耗的CPU 时间Trec差不多;和预期的一样,WENO-ACM 的映射消耗时间(Tmap)非常低,仅为3%～ 5%.上述结果表明,传统加映射的WENO 格式由于映射操作消耗的CPU 时间是非常惊人的,这一结论与文献[33]中给出的测试结果是一致的.此外,还可以看到: 其他部分(Toth)占用的时间是最少的且几乎是恒定的,约0.063 s;二维黎曼问题的特征分解以及特征空间与物理空间来回投影部分(Tch)占用的时间在0.2 s 左右,而双马赫反射问题则在0.24～0.27 s 左右.

3.6 具体复杂问题验证

最后,对WENO-ACM 模拟具体的复杂问题进行验证,这里选择竖直平面激波与热层作用[15]问题进行模拟.

问题描述: 如图17 所示,在[−5 m,5 m] × [−5 m,5 m]的区域布满了理想完全气体.流场中存在物质界面P1OP2(图中虚线所示),点O与坐标原点重合,点P2固定在(0 m,−5 m)处,点P1位于x=5 m 上,坐标记为(5 m,y0).初始时刻,整个流场内的介质处于静止状态,且各处压力均为100 kPa,比热比均为1.4.界面左侧气体密度为1.00 kg/m3,右侧的气体被加热形成形状不规则的热层,因此其密度降低为0.25 kg/m3.马赫数2.0 且强度恒定的平面激波沿x轴正向从左向右传播,假设其到达界面OP2处时的时刻为t=0.已知平面激波后流场压力为450 kPa,密度为2.667 kg/m3,速度467.7 m/s,比热比为1.4.除左侧为入流边界外,其他三侧均为出流边界条件.现在取y0=2.886 8 m,模拟t=4.0 ms 时的流场分布状态.

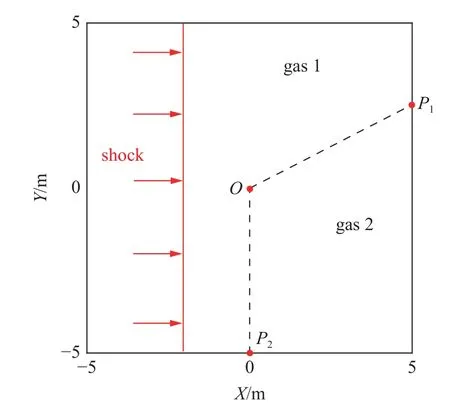
图17 竖直平面激波与热层作用示意图Fig.17 Illustration of the interaction of a vertical planar shock with a thermal layer

针对这一典型的涉及复杂流场的力学问题,采用成熟商业软件Autodyn 及本文提出的WENOACM 格式进行了模拟,其中Autodyn 和WENOACM 分别采用了400 万和25 万的均匀网格,图18中给出了密度的模拟结果.作为对比,图中还给出了相同计算条件下WENO-M 和WENO-PM6 的模拟结果.由图18(a) 和图18(d) 可见,尽管WENOACM 的网格数量只有Autodyn 的1/16,但其模拟结果与Autodyn 是相当的,甚至在局部位置(如图18(a)中红色虚线框区域) WENO-ACM 的模拟分辨率要高于Autodyn.可以看到,在图18 中WENO-M 和WENO-PM6 的模拟结果与WENO-ACM 非常接近,几乎难以直接观察到它们之间的区别.

图18 Autodyn 和WENO-ACM 计算所得流场密度分布Fig.18 Density distribution computed by Autodyn and WENO-ACM

此外,如图18(a)中粉色点划线所围区域所示,Autodyn 的模拟结果在激波后方出现了明显的数值扰动现象,而图18(d)所示的WENO-ACM 的模拟结果中似乎不存在这样的扰动.为了进一步验证这一点,在图19 中画出了Y=4 截面上Autodyn,WENOACM 以及WENO-M 和WENO-PM6 的密度变化曲线,其中参考解是采用1000 × 1000 网格的WENOJS 格式的模拟结果.由图19 可以清楚的看到,在激波后方,Autodyn 出现了显著的数值扰动,而WENO-ACM 则成功的避免了这些数值扰动.

由图19 可知,WENO-M 和WENO-PM6 同样能够避免上述数值扰动,但仔细观察可以看到,WENO-M 的分辨率要低于WENO-ACM,WENOPM6 的分辨率非常接近但略微低于WENO-ACM.此外,如前所述,WENO-ACM 相比于WENO-M 和WENO-PM6 的另一个显著的优势是其具备更高的计算效率.为了验证这一点,针对本算例同样进行了计算效率测试,结果如表10 所示.由表10 可见,WENO-ACM 相对WENO-JS 的额外计算时间控制在5% 以内,而WENO-M 和WENO-PM6 相对WENO-JS 的额外计算时间则分别达到了30% 及70%,远远高于WENO-ACM 的结果.显然,这一结果与前面的结论是一致的.

图19 Y=4 截面上的密度变化曲线比较Fig.19 The cross-sectional slices of density plot along the plane Y =4

表10 每个Runge-Kutta 步的CPU 计算时间(s)及相对WENO-JS 的额外计算时间(竖直平面激波与热层作用问题)Table 10 CPU time (s) and the extra computational cost per Runge-Kutta step for the interaction of a vertical planar shock with a thermal layer

以上结果成功的验证了WENO-ACM 格式在模拟具体的复杂问题时,具有很好的鲁棒性以及非常高的分辨率.同时,相对文献中已有的加映射的WENO 格式,WENO-ACM 格式在计算效率方面有明显的优势.

4 结论

本文给出了一种全新的加近似常值映射的WENO 格式,称为WENO-ACM.借助符号函数的一种近似函数,构造出了一种全新的映射函数.该映射函数完全满足传统映射函数构造过程中关键的约束条件,因此,其相应的WENO-ACM 格式能够获得最佳收敛精度.最重要的是,由于在大部分情况下,新的映射函数只需要一次赋值运算操作,因此可以极大的降低计算消耗,进而提高计算效率.数值测试结果表明,WENO-ACM 能够极大的减少相对WENOJS 格式的额外计算消耗.此外,本文推荐的WENOACM 还能够显著降低数值耗散,进而提高计算结果的分辨率.