涡识别技术及其在船用螺旋桨伴流场中的应用1)

杨 琳 郑 兴

(哈尔滨工程大学船舶工程学院,哈尔滨 150001)

引言

旋涡的概念与流体动力学的主题一样古老,但是仍然缺乏公认的旋涡定义.关于湍流中旋涡是由什么构成的,长期以来存在相当大的困惑.通常可以将湍流中的拟序结构(coherent structure,CS)视为旋涡,实践中必须首先确定湍流中动态显著的大尺度旋涡区域,而这又需要对旋涡进行客观定义.一般来说旋涡的客观定义应允许使用涡动力学概念来推导和解释CS 的形成与演化,探索CS 在湍流现象中的作用,为湍流现象开发可行的湍流模型和控制策略.湍流被视为涡流细丝的缠结,并且使用涡动力学的概念可以很好地解释湍流物理学的许多方面[1].通过描述CS 的形成、演化及其与背景湍流的耦合过程,有望了解各种湍流现象,例如夹带(entrainment)和混合、传热和传质、化学反应和燃烧、阻力以及空气动力学噪声的产生,而且还可以对湍流进行可行的建模[2].

直觉上涡流被认为是一个管,其表面由涡线组成[3],然而涡流管的存在并不意味着涡流的存在,例如层流管流中的涡流管在任何情况下都不是涡流.Lugt[4]将旋涡定义为围绕一个公共中心旋转的大量物质颗粒;Chong 等[5]将其定义为 ∇u的复特征值区域;Hunt 等[6]将其定义为一个区域,同时包含 ∇u的正第二不变量和低压;Jeong 等[7]根据对称张量的特征值定义它,其中S和 Ω 分别是速度梯度张量 ∇u的对称和反对称部分.

研究已经发现湍流剪切流主要由空间连贯的和随时间变化的旋涡运动所主导,通常表现为CS[8-10].在物理实验和数值模拟中已经提出了几种用于CS 生成的条件采样技术[11-16].在过渡流中,CS 生成相对简单,因为CS 的发生在时间和空间上具有规律性,诸如速度之类的参考信号可以用作生成的触发信号[17-18];但是在充分发展的湍流中,例如射流(jets)、伴流(wakes)和混合层(mixing layers)的远场区域,要得到动力学意义的旋涡结构,瞬时涡度场是必不可少的[19-20],遗憾的是即使是瞬时涡度场也不足以揭示湍流边界层中的CS[21].

认识到黏性流体中旋涡的大小取决于所选识别器的阈值,并且大量研究表明湍流中涡旋 C S 的核在空间中定位良好,故选取仅识别涡旋核.涡旋核的存在一般要满足两个要求: (1)涡旋核必须具有净涡度及净环量;(2)识别出的涡旋核的几何形状应该是伽利略不变的.遗憾的是这些要求不会导致单一的识别方法,仅将这些要求用作对可能潜在识别方法的初步检查.

国内对涡识别技术的理论研究及应用相对较少,在百度学术上搜到的近年公开发表的关于这方面的研究见文献[22-24];杨越[22]总结了湍流中目前主要的涡识别方法,提出了涡识别和相关涡动力学的重要科学问题,并展望了湍流中涡动力学与相关湍流预测模型的发展趋势;王义乾等[23]讲到了第三代涡识别方法及其应用综述;刘超群[24]回顾了涡定义和涡识别方法的发展历史,着重介绍了美国德州大学阿灵顿分校团队及其合作者在涡科学和湍流研究的一些最新学术创新成果.国外最新公开发表的关于涡识别方面的研究见文献[25-35].尽管目前存在一些涡识别技术的研究,也有人提出一些新的识别方法,但是在现实中大部分人还是没有很好地去理解什么是涡及如何去识别它们这两个问题;且涡识别技术里包含许多深层次的数学及物理认识,还远没有到下结论的时候,值得更多的研究者去深入探讨.

本研究旨在船用螺旋桨的伴流场中,从理论和实践上寻找一种可行且有效的涡识别方法.如何识别一船用螺旋桨伴流场中的旋涡？本文作者围绕这一问题进行了深入的探讨,从理论上研究了六种涡识别方法,如表1 所示,并讨论了各种识别方法的优缺点.为了更好地说明涡识别技术的合理性,本文还使用了一些解析解、Burgers 涡流解和Lamb-Oseen涡流解.

表1 涡识别方法Table 1 Methods of vortex identification

1 研究方法

1.1 控制方程与数值方法

伴流场基于纳维−斯托克斯(N −S)方程组的数值模拟,采用一个局部动态k方程大涡模型(large vortex simulation,LES)[36],在物理空间中,笛卡尔坐标系x=(x1,x2,x3),下速度场为u=(u1,u2,u3),质量守恒及动量守恒方程(不计体力)分别为

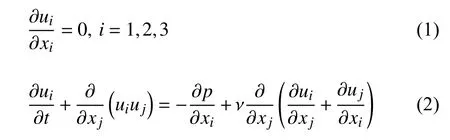
其中,p为静压,ν 为运动黏度并假设其为常数.根据不同的时空分辨率和动力学描述,LES 仅用于直接计算空间中的低频模式,如果忽略滤波器和空间导数之间的换相误差,过滤后的质量守恒及动量守恒方程分别为[37]

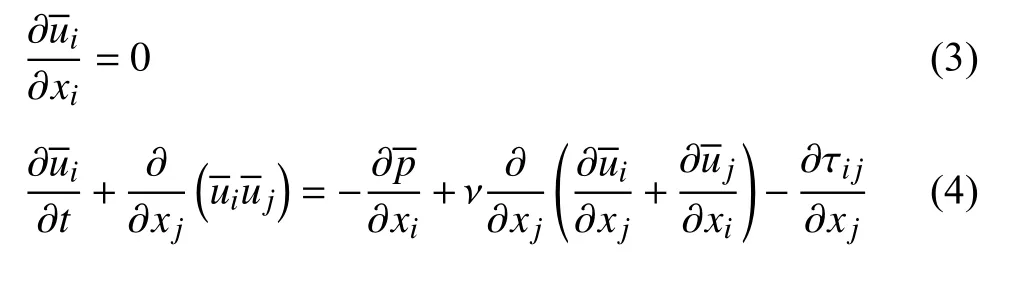
其中亚格子尺度(subgrid scale,SGS)应力张量 τ 和亚格子尺度动能kSGS方程分别为

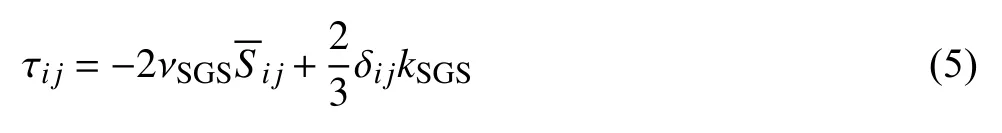
其中,νSGS为亚格子涡黏度,ε 为亚格子动能耗散率.

LES 基于大尺度和小尺度之间的分离,其中直接模拟具有较高能量的大尺度湍流结构(各向异性湍流),而小尺度湍流则使用亚格子尺度模型进行建模.小尺度湍流波动本身被平滑,并通过涡流黏度和扩散率假设进行建模.特征尺寸大于截止长度的尺度称为大尺度或分辨尺度,其他尺度称为小尺度或亚格子尺度.SGS 通过统计亚格子尺度模型将其包括在内,SGS 的精确建模是可能的,因为在较小的尺度(低于过滤器宽度)下,湍流可以被认为是各向同性的,与流动类型和边界条件无关.LES 就是对过滤后的 N −S 方程中非线性项进行分解,然后对未知项进行建模.

本文研究了一种五叶右旋船用螺旋桨DTMB 4381[38](变桨距、无侧斜、无尾斜)的伴流场.在无量纲半径r′=r/R=0.2 ∼1 处,叶片在与螺旋桨同轴的圆柱面上的截面为翼型,如图1 所示,其中R是螺旋桨盘半径,桨毂呈锥形.相对弦长c′(用螺旋桨直径D无量纲化,即c′=c/D)和扭角 θT的分布如图2 所示.为了消除数值水筒的阻塞效应,计算域的设置如图3 所示,图中也给出了流域的初始边界条件.为了能捕获所关心的伴流涡,网格划分示意如图4 所示,计算域内不同区域网格的大小见表2.注意,后面“结果与分析”中给出的螺旋桨伴流场的涡识别结果是在此螺旋桨的设计工况下得到的,即计算域入口处的来流速度U=4.5 m/s,螺旋桨的进速系数J=0.9,对应桨的转速约1500 r/min.

图1 螺旋桨几何Fig.1 Geometry of blade,hub and shaft

图2 叶片沿径向相对弦长和扭角分布Fig.2 Distributions of relative chord length and twist angle along radial direction

图3 计算域及初始边界条件Fig.3 Computational domain and initial boundary conditions

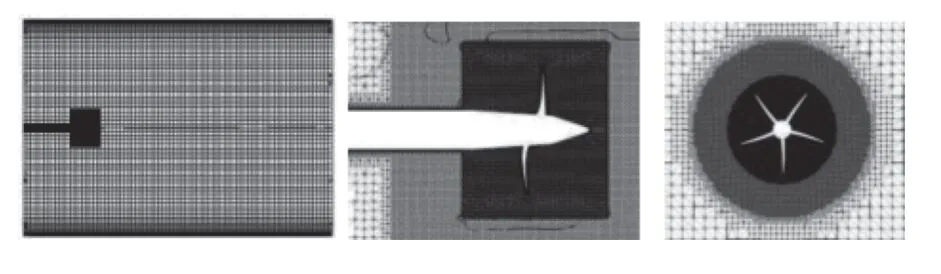
图4 网格划分示意Fig.4 View of meshing

表2 计算区不同域网格尺度Table 2 Overall cell scales in different regions of computational domain

1.2 涡识别方法

在笛卡尔直角坐标系x=(x1,x2,x3)=(x,y,z) 下,若速度向量为u=(u1,u2,u3)=(u,v,w),则速度梯度张量T为

速度梯度张量T的对称部分S和反对称部分 Ω 分别为

对称张量S称为应变率张量,其主对角线上的分量代表线应变变化率,其余分量代表角变形率;线应变率反映拉压,角变形率反映剪切,两者相互关联;单位体积流体微团在单位时间内的体积变化率为张量S的第一不变量,流体微元体的体积只受线应变率的影响,而不受角变形率影响,角变形率仅引起剪切或角度变形.反对称张量 Ω 中仅包含三个不同的分量,对应一个矢量 ζ=rotu/2,描写微团的瞬时角速度;由于速度的旋度与微团瞬时角速度之间的这种联系,它可以作为流体涡旋运动强度的度量,称之为涡强度或涡度,即有 ω=rotu=2ζ.

1.2.1 局部最小压力标准

Robinson[21]使用DNS 数据库显示: 低压标准有效地捕获了湍流边界层中的旋涡结构,但是通常无法指定适当的压力水平来识别流动中的所有旋涡区域.最小压力标准的基础是: 在受离心力和压力平衡(所谓的回旋平衡)的情况下,压力趋向于在回旋运动的轴上具有局部最小值,此标准仅在定常无黏平面流中严格正确.压力可能在某个点的所有方向上都具有最小值(所谓在三维度上局部最小压力的概念),或者仅在垂直于涡旋轴的平面(例如Burgers涡)中具有最小值,仅讨论平面中的最小值,此时对应的限制较少,且可能也包括前一种情况.最小局部压力标准的不足之处可以通过四个简单例子进行说明: (1)在非定常无旋流动中,存在一个明确定义的压力最小值,考虑具有驻点的非定常无旋轴对称流动

积分 E uler 方程,可得压力为

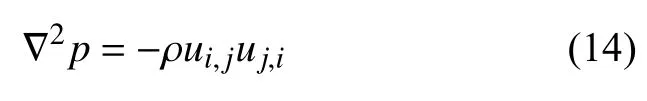
控制的(此处的下标逗号表示偏微分,并且对指标使用求和约定),因此压力固有地具有比涡度更大的尺度.

1.2.2 流线或迹线标准

Lugt[4]提出使用封闭或螺旋路径来检测旋涡,但是流线或迹线显然不能满足伽利略不变性.该检测的另一个严重不足之处是,当旋涡由于诸如配对(pairing)、撕裂(tearing)等非线性过程分解,粒子在涡流的生命周期内可能无法完成围绕旋涡中心的完整旋转,没有闭合的迹线.在涡流相互作用的重新连接区域,特别是在高R e时,由于快速改变的旋涡线拓扑结构,流线和迹线即使在最佳的参考系中也可能会高度扭曲,从而逃避被识别,而这些被忽略的区域可能在动力学上反而变得更加重要[41].

1.2.3 涡度值标准

涡度大小(| ω|)已被广泛用于推导CS 并代表涡旋核[42-43],这种方法在自由剪切流中相当成功,但可能并不总是令人满意,因为如果背景切变与涡旋内的涡度大小相当的话,| ω| 不能在剪切流中识别出涡旋核.Lugt[4]研究表明在平面边界壁流中 | ω| 最大值和最小值仅出现在壁面上,Jimenez等[44]研究表明在湍流边界层中最大值 |ω| 出现在高速条带区域附近,然而在这两种情况下,边界附近的流动都以剪切为特征,没有表现出旋动,故 | ω| 也不是边界层中涡识别的合适标准.即使在自由剪切流中,从 | ω| 表面识别旋涡也存在潜在的困难,例如,涡片(vorticity sheet)不是涡旋(vortex),即使它可能具有很大的涡度值.

1.2.4 张量T的复特征值

由于速度梯度张量 ∇u是伽利略不变量,Chong等[5]使用速度梯度张量 ∇u的特征值对流场中任何点周围的局部流线模式进行分类(参考系随该点的速度移动),并提出涡核是一个具有复特征值的区域,复特征值表示局部流线样式在随点移动的参考系中是闭合的或螺旋形的.∇u的特征值满足特征方程(10),其中P=ui,i=0 (对不可压缩流)、和它们分别是速度梯度张量的三个不变量,当判别式

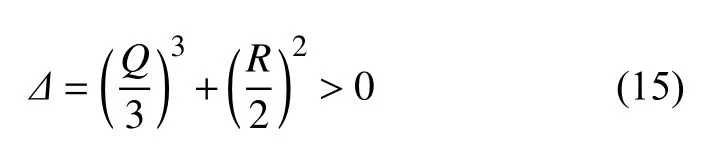
为正值时,即存在复数特征值.

1.2.5 张量T的第二不变量Q或运动涡度数Nk

Hunt 等[6]定义涡流是具有 ∇u的正第二不变量(Q>0)的区域,其附加条件是压力低于环境值.Q定义为

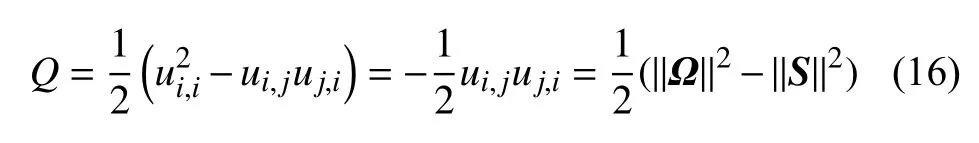
表示剪切应变率和涡度大小之间的局部平衡,可以很容易地看出,与 | ω| 标 准不同,Q在壁面上消失了,即在壁面上的剪切应变率和涡度具有相同的大小.一般壁面上的速度梯度可以写为

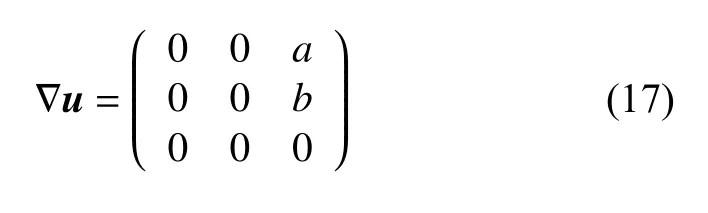
使得在壁面上有Q=0,这必然意味着 ∆=0,因为在壁面处R=0,故基于 ∆ 和Q的定义不会出现 | ω| 定义无法正确地表示壁面附近的涡旋运动问题.Truesdell[45]引入了运动涡度数N k来测量旋涡质量,而不是 ∥Ω∥给出的局部旋转速率,他将N k定义为

式中,N k是 | ω| 的逐点度量,通过应变率的范数进行归一化处理,从而给出了旋涡质量,它与旋涡强度无关,例如N k=∞ 和N k=0 分别对应于固体旋转和无旋运动,与 | ω| 的值无关.Melander 等[46]在研究涡核动力学时,将轴对称旋涡圆柱的核心确定为N k>1 的最大连通空间区域.从方程(18)可知,N k>1 的区域与Q>0 的区域相同,但是由于N k通过应变率的大小进行了无量纲化,因此N k峰值忽略了旋涡动力学意义,换句话说只要旋涡质量相同,N k就不会区分不同涡度大小或环量的涡.Q也可以解释为 N −S 方程中的压力源项,根据压力泊松方程(∇2p=2ρQ)和其最大原理,如果Q>0,最大压力仅出现在边界上;如果Q<0,最小压力仅出现在边界上.但是Q>0,并不一定意味着在该区域内会出现压力最小值,最小压力可以出现在Q>0 区域的边界上,故在Q>0 的区域和最小压力的区域之间没有明确的联系.从这个意义上说,Hunt 等[6]和Melander 等[46]使用的定义严格来说并不完全相同,即使在大多数情况下它们是等效的.从方程(15) 可以看出,条件Q>0 比∆>0更具限制性,尽管哪个定义更合适尚无先验.

1.2.6 张量S2+Ω2的特征值 λ2

如前所述,尽管不能将压力局部最小值标准用作涡核识别的一般检测标准,但是它却为寻求合理的涡核识别提供了起点.局部最小压力的存在并不表示涡核的存在,导致它们之间这种不一致性的主要原因有两个: (1)非定常应变,它可以在不涉及涡旋运动的情况下产生最小的压力;(2)黏性作用,它可以消除涡流运动中的最小压力.通过简单地丢弃这些影响,可期望获得关于旋涡存在的更好标准.由于有关局部压力极值的信息包含在压力的Hessian(p,ij)中,考虑p,ij的方程,取 N −S 方程的梯度可得

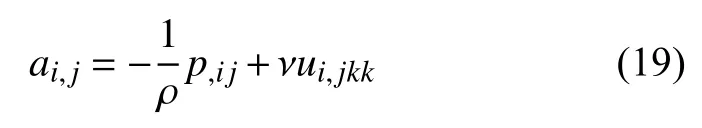
其中,a i,j为加速度梯度,p,ij对称,a i,j可以被分解为对称和反对称部分

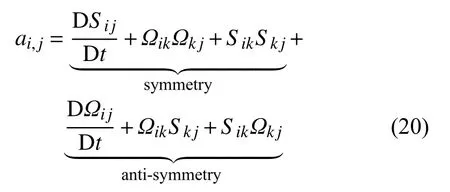
反对称部分是涡度输运方程,对称部分可表示为

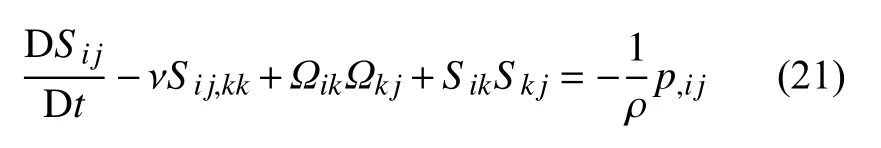
在平面中,局部最小压力的出现需要张量p,ij的两个正特征值.式(21)左侧由于第一项表示非定常无旋应变,第二项代表黏性作用,将不考虑,仅通过考虑来确定是否存在由于旋涡运动引起的局部压力最小值,并认定涡核为具有的两个负特征值的连接区域.由于是对称的,因此它仅具有实特征值,即有 λ1≥λ2≥λ3,则可定义涡核内 λ2<0 的标准,可得[45]

表3 基于负 λ2 和正 Q 标准识别涡核对比Table 3 Comparison of vortex core identifing results based on negative λ2 and positive Q criteria

在平面流中,由负 λ2与 ∇u的复特征值和正Q定义的区域是等效的,如考虑平面流的一般速度梯度式

∇u的特征 值σ 的特征 方程为σ2+Q=0,其 中Q=−(a2+bc),故σ=±(−Q)0.5,Q>0 时∇u为复特征值,由式

负 λ2要求a2+bc<0,即Q>0,故对于平面流这三个定义等价.

2 结果与分析

2.1 基于局部最小压力标准

此标准通过Burgers 涡流[48]和Lamb-Oseen 涡流[49]两个简单例子进行说明,见图5.轴对称 Burgers旋涡代表了完整的 N −S 方程的少数已知精确解之一,涡流由纯涡叠加在无旋转的背景应变流上组成,该流动是不可压缩的,在柱坐标系中,长度是相对于Burgers 长度尺度的无量纲化,时间是相对于a−1的无量纲化,其中a是背景流场的应变率,其解可以写为

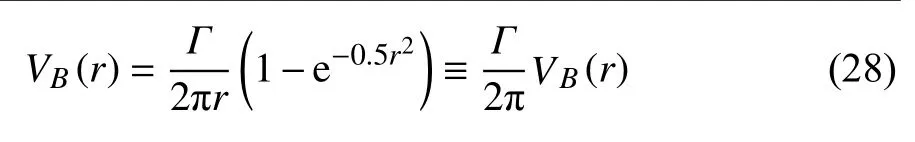
其中,Γ 为环量,ν 为流体黏度.Lamb-Oseen 涡流的方位速度可写为

此解对应于 N −S 方程的自相似解,半径随时间增加,有a2(t)=a2(0)+4νt.这里背景流扩散被忽略了,涡流被认为是冻结的,a恒定,黏度的影响由雷诺数来表征.进行无量纲化,取涡旋半径a=1 和环量 Γ=2π ,角速度和轴向涡度分别可表示为

对于Burgers 涡流,由于没有旋转应变率,涡承受轴对称张力,而张力通过涡的扩散来平衡[50];涡核的长度尺度是固定的,压力峰值的长度尺度,即∂p/∂r=0点的半径(图5(a)),随着轴上涡度的增加而增加.Lamb-Oseen 涡流是从初始线涡开始衰减的轴对称涡流[3](图5(b)),当半径r=4(νt)0.5时,相对涡度ω′几乎消失,而相对压力p′仍有一个显著值(最大负值约为0.25).可以看出,涡核和相关局部低压区域之间存在固有的比例差异,这使得使用局部最小压力标准进行涡识别成为一个问题.

图5 相对涡度和压力分布(实线为涡度,虚线为压力,黑虚线为ω0=1,向下橙紫绿黄蓝 ω0 分别为 2,3,···,6)Fig.5 Relative vorticity and pressure distribution (solid line is vorticity;dotted line is pressure;black dotted line is ω0=1 ;downward orangepurple-green-yellow-blue lines are ω0=2,3,···,6 respectively)

2.2 流线或迹线标准

图6 中显示出了在三个不同移动参考系中的轴对称Lamb-Oseen 涡流的流线型式.使用流线或迹线标准识别涡,将模糊在不同参考系下的涡流,并不可避免地在包含不同速度的多涡平流的湍流中会失败.

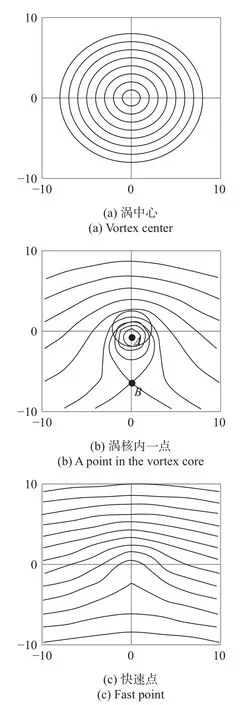
图6 Lamb-Oseen 涡在不同参考系下的流线(快速点比任何一点的速度都快)Fig.6 Streamline of vortex under different reference systems (the speed at the fast point is faster than that at any point)

2.3 涡度值

螺旋桨伴流中的涡度等值剖面如图7 所示,可见桨轴向涡度变化很大,具有强大的核心动力学特性[47].尽管实际桨毂区域只有一个连续的涡流柱,但考虑到 | ω| 值的设置具有一定的随意性,等值面可能沿着涡旋轴终止并被分成多段,有必要设置不明确的足够低水平 | ω| 值来识别涡,这是涡度值标准识别涡的缺点.

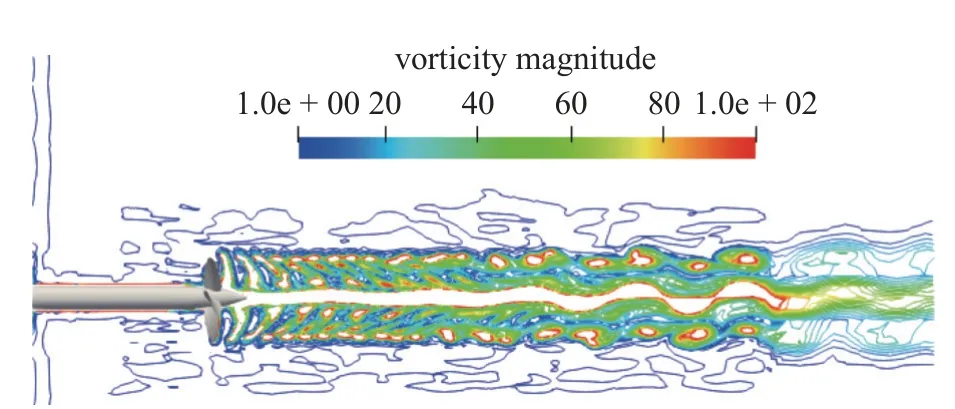
图7 涡度大小等值面Fig.7 Contours of vorticity magnitude

2.4 张量 T 的复特征值

为了对此标准涡识别方法进行物理解释,考虑运动参考系中Lamb-Oseen 涡的流线,见图6(b).在以相同速度移动的粒子A和B的参考系中,涡流核心内的A周围出现闭合的流线型态(用粗线标记),表示正 ∆,而在涡流核心外的B处出现了鞍形,∆ 为负.

2.5 张量 T 的第二不变量 Q 或运动涡度数 Nk

螺旋桨伴流中的Q=0 剖面如图8 所示,可见叶尖涡、叶片后缘涡和毂涡都清楚地被识别,也可看出他们之间的相互诱导作用,与图7 有明显差别.在螺旋桨下游大约1D后,叶尖涡和后缘涡之间的相互作用变得模糊;在2D之后,毂涡、叶尖涡和后缘涡相遇,进一步模糊尾迹;尾迹近场主要形成一些小半径涡核,远场中涡核直径增大,轴中心的涡核半径在下游增加得更多.

图8 涡核识别 Q=0Fig.8 Vortex core identification Q=0

2.6 张量 S 2+Ω2 的特征值 λ2

螺旋桨伴流中的 λ2=0 剖面如图9 所示,可以看出其与图8 的高度一致性,说明采用Q标准和 λ2标准对于螺旋桨伴流中涡识别基本等效.

图9 涡核识别 λ2=0Fig.9 Vortex core identification λ2=0

3 结论

(1)局部低压标准比较直观,但深究考虑其黏性和非定常的影响后,明显不足;迹线或流线显然不能满足伽利略不变性,会使辨别变得混乱;涡度大小需要规定其阈值,具有一定不确定性,且也会识别不是涡的涡片;张量T的复特征值也会有识别不出的区域;速度梯度张量的第二不变量Q标准和对称张量的第二特征值λ2标准能更好地识别涡核,这两种标准有时等效.

(2)对于船用螺旋桨的伴流采用Q标准和 λ2标准等效,都能很好地捕获螺旋桨伴流中的涡核,且能很好地解释螺旋桨尾流涡脱落的机理.