考虑电场梯度的挠曲电纳米板弯曲性能分析1)

曹彩芹 陈晶博 李东波

(西安建筑科技大学理学院,西安 710055)

引言

力−电耦合效应通常用于传感器、滤波器、谐振器和俘能器[1-8]等智能器件的设计中,这些器件又被称为微/纳机电系统(micro/nano-electro-mechanical system,MEMS/NEMS)器件.在过去的几十年里,作为介电材料中力−电耦合效应的一种类型,压电效应已经成功的应用于这些器件的设计之中[9].然而压电效应只存在于20 种非中心对称晶体中,且压电器件要求工作温度低于压电材料的居里点,这些限制了MEMS/NEMS 器件设计中材料的选择范围[10].相较于压电效应,挠曲电效应(应变梯度和电极化之间的耦合)在固体介电材料中普遍存在,由于应变梯度与空间尺度成反比,因此挠曲电性存在有显著的尺度依赖特性,在宏观尺度上,压电效应更显著,而挠曲电极化的量级通常为10−9C/m2,随着材料或结构尺寸减小到微纳米尺度,材料或结构的挠曲电效应明显增大,和压电效应相比不容忽视[11-12].挠曲电效应的特性大大拓展了微纳米器件材料的选择范围.

挠曲电理论研究应变梯度和电场变量之间的耦合关系.基于应变梯度理论的经典挠曲电理论定义了一个四阶挠曲电张量[12-16],其描述了电极化和应变梯度之间的耦合关系.然而,该理论包含过多的独立材料参数,在实际应用中难以测定.21 世纪初,基于偶应力的挠曲电理论得到了研究人员的关注,该理论包含了一个三阶挠曲电张量,描述了电位移和曲率(旋转梯度)之间的力−电耦合关系,并且减少了独立材料参数的个数.此外,对于弹性介电材料,在本构方程中,可以同时包含力学变量梯度和电学变量梯度.Maranganti 等[17]提出了基于极化梯度理论和应变梯度理论的一般方程.2020 年以来,基于应变梯度的挠曲电理论三维框架被用于分析和求解梁(杆)的静态弯曲和扭转问题[18-21].Li 等[22]在各向同性介电材料的偶应力和极化梯度理论框架内提出了一个通用的挠曲电理论.Qu 等[23]首次在偶应力和电场梯度的理论基础上提出了弹性介电材料的非经典理论,挠曲电理论被传统的偶应力理论重新定义并用于解释微观效应和力−电耦合效应.

鉴于挠曲电材料在微纳米尺度下卓越的力−电耦合特性,挠曲电材料选材的广泛性,以及在MEMS/NEMS 器件中广泛使用的薄梁和薄板通常在微纳米尺度上表现出与微观结构相关的尺度依赖效应,因此,本文以二维纳米矩形板为例,根据弹性介电材料的非经典理论[23]进行建模,分析二维矩形板在弯曲问题中的力−电耦合行为,重点研究电场梯度对纳米板中电势的影响.首先,由Mindlin 假设给出二维板位移场和电势场的一阶截断表达式,基于此推导应变、曲率、电场、电四极矩的表达式.选取中心对称的立方晶体(m3m 点群)作为弹性介电材料,得到二维本构方程.利用弹性电介质变分原理得到纳米矩形板的控制方程和板边界上的线积分等式,将二维本构方程代入控制方程推导出以基本未知量表示的板的控制方程;将纳米矩形板边界上的方向余弦代入到线积分等式,得到四边简支矩形板的边界条件.利用得到的四边简支矩形板的控制方程和边界条件,求解纳米矩形板的弯曲问题,以期为新型微纳智能器件的设计提供参考.

1 理论分析

1.1 纳米矩形板的基本物理量

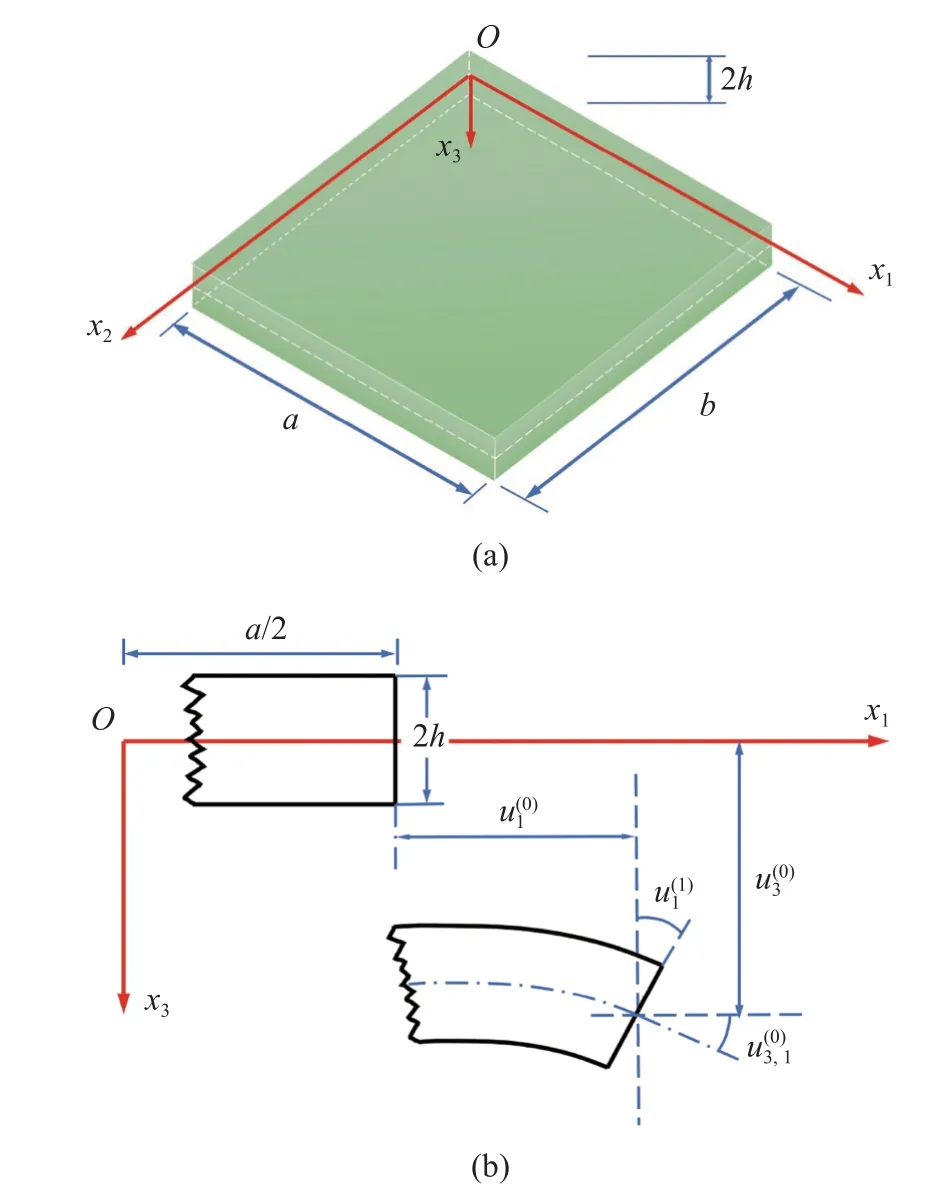
图1 (a) Mindlin 板中面上的直角坐标系和(b) 变形前和变形后板在x2=0 平面上的几何形状Fig.1 (a) Rectangular coordinate system on the midplane of Mindlin plate and (b) geometry of the plate edge on the x2=0 plane before and after deformation

根据式(1)给出的板的位移场和电势场,分别计算得到无穷小应变张量S的分量、旋转矢量θ的分量、曲率χ的分量、静电场电场强度E和电场梯度V的分量.

无穷小应变张量S(=0.5(∇u+u∇))的分量为

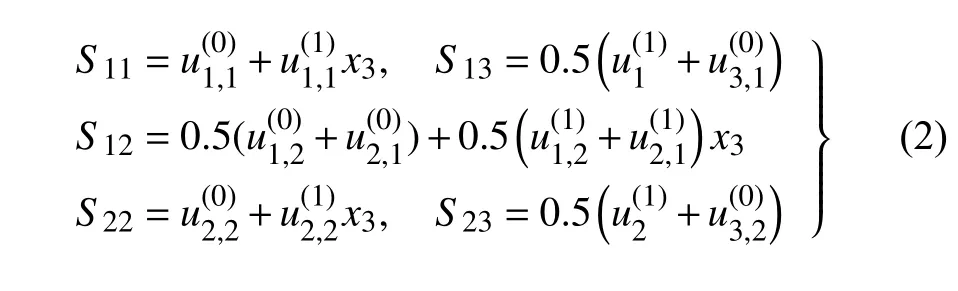
式中,下标“,1”表示该变量对x1方向求偏导数,即∂()/∂x1,其余类似.

根据经典偶应力理论[29-30],旋转矢量θ(=0.5·(∇×u))的分量为

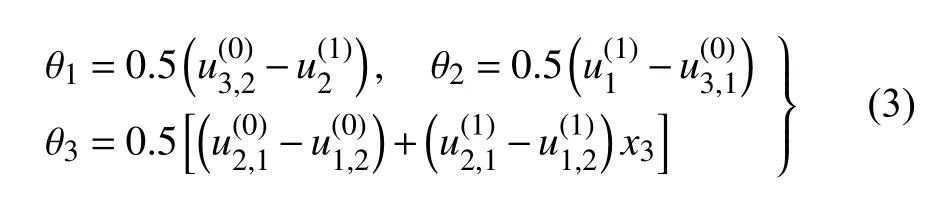
曲率χ的计算公式为χ=θ ⊗∇,其相应的分量形式为

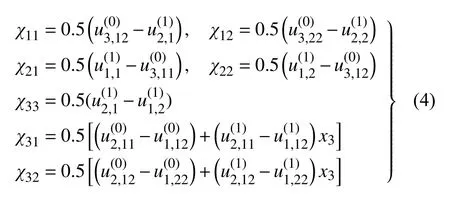
静电场电场强度E(=−∇φ)和电场梯度V(=E⊗∇)的分量分别为[23]

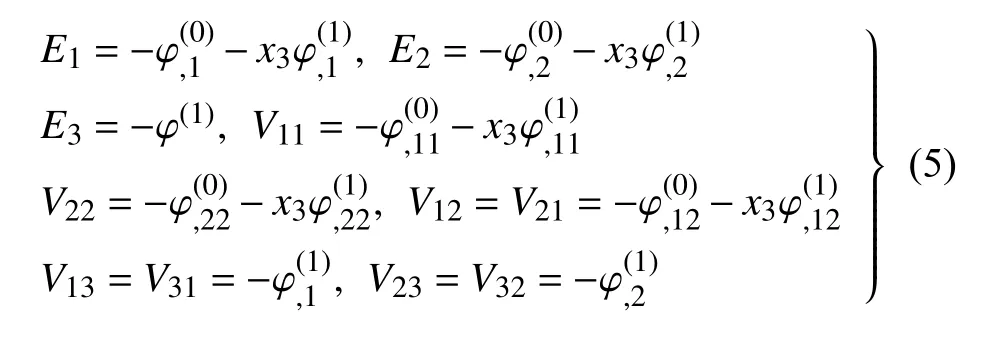
1.2 弹性介电材料的二维本构方程

弹性介电材料的广义三维本构方程为[23]

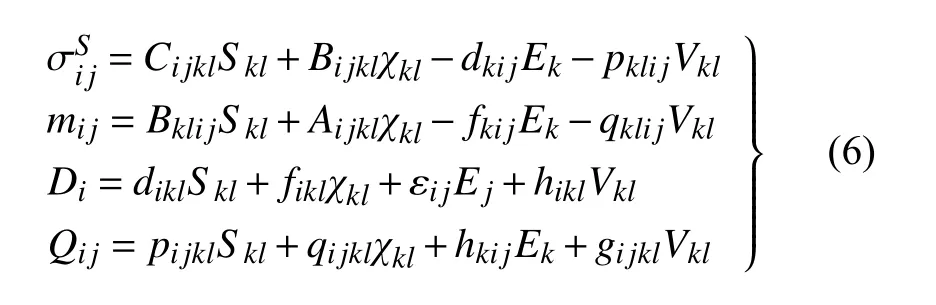
式(6)中使用了爱因斯坦求和约定,i,j,k和l为指标符号,范围从1 到3.,mij,Di和Qij分别是对称的应力张量分量、偶应力张量分量、电位移矢量分量和电四极矩张量分量.Skl,χkl,Ek和Vkl分别是无穷小应变张量分量、无穷小曲率张量分量、电场强度分量和电场梯度分量,Aijkl,Bijkl和Cijkl是4 阶弹性刚度矩阵分量,pijkl和qijkl是4 阶电−梯度耦合张量分量,gijkl是4 阶电四极子系数分量,dikl是3 阶压电张量分量,fikl是3 阶挠曲电张量分量,不同于一般的4 阶挠曲电张量分量fijkl,fikl描述的是弹性介电材料中电位移Di与曲率(旋转梯度)χkl之间的关系.hikl是3 阶电−梯度耦合张量分量,εij是2 阶介电张量.选取中心对称的立方晶体(m3m 点群)作为弹性介电材料,由于介电材料是中心对称的,有Bijkl=0,qijkl=0,dikl=0,hikl=0,同时为了突出创新性,不考虑微结构效应(Aijkl=0,其已在文献[31] 中得到研究),pijkl代表的是逆挠曲电效应,由于主要关心外力引起的弯曲以及曲率引起的电极化,因此没有考虑逆挠曲电效应(pijkl=0).

立方晶体(m3m 点群)的材料参数如下所示

式(7)中使用了Voigt 符号,Cpq和gpq中p,q的取值范围从1 到6,fip中p的取值范围从1 到9,弹性刚度矩阵Cijkl与Cpq、电四极矩系数矩阵gijkl与gpq的指标对应关系为: 对于指标ij或者kl,有11→1,22→2,33→3,23(32)→4,31(13)→5,12(21)→6.3 阶挠曲电张量fikl与fip的指标对应关系为: 对于指标kl,有11→1,12→2,13→3,21→4,22→5,23→6,31→7,32→8,33→9,即f123=f231=f312=−f132=−f213=−f321=−f16.

根据Mindlin 板理论,定义如下高阶应力、高阶偶应力、高阶电位移、高阶电四极矩和高阶外力

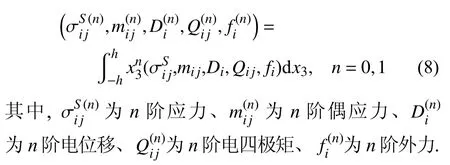
将广义三维本构方程式(6)代入式(8)中,得到板的二维本构方程.零阶应力和一阶应力本构方程为

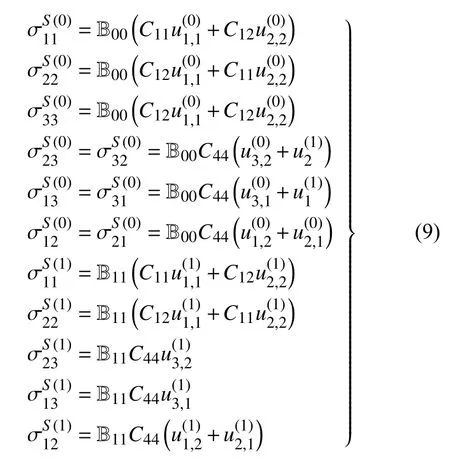
零阶偶应力和一阶偶应力本构方程为

零阶电位移和一阶电位移本构方程为

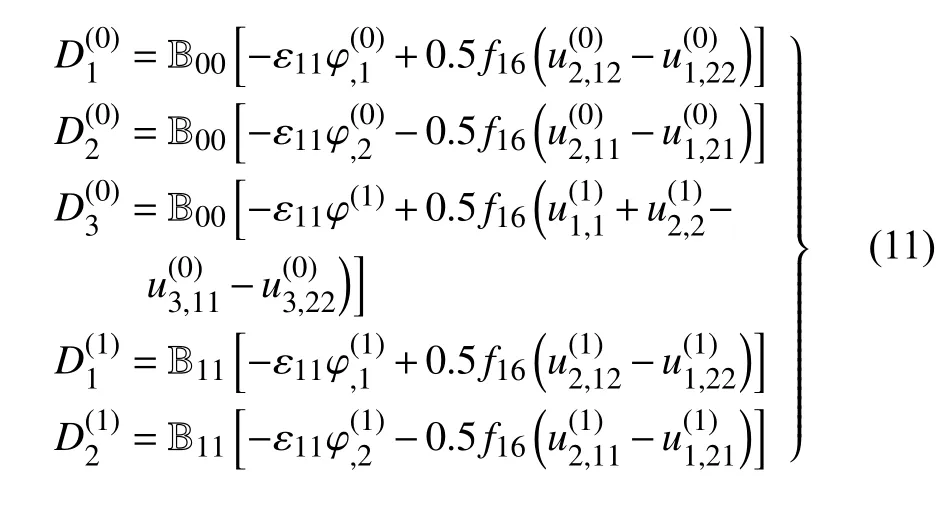
零阶电四极矩和一阶电四极矩本构方程为

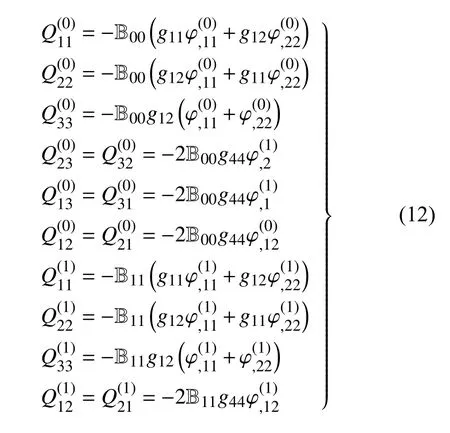
其中式(9)～ 式(12)中的参数 Bmn为

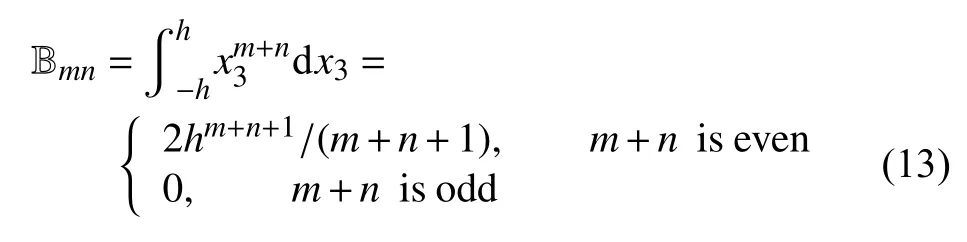
1.3 纳米矩形板弯曲问题的控制方程

弹性变形板电学焓的一阶变分可以表示为[23,32]

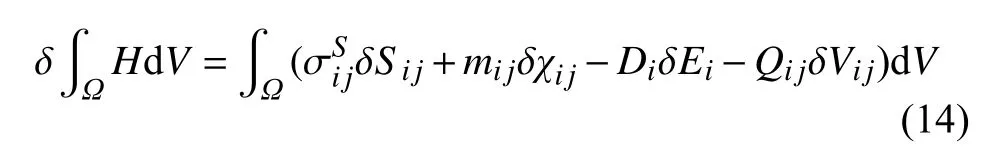
其中H为电焓密度,Ω表示板所占据空间的体积,dV是体积微元.

外体力fi做的虚功可以表示为

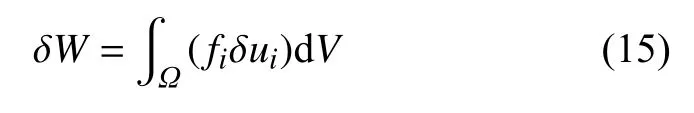
根据Mindlin 的电介质变分原理[33-34],有

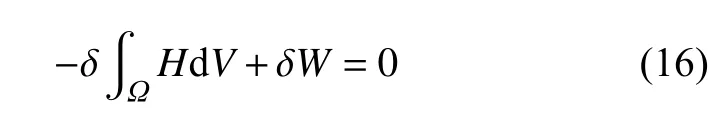
将式(1)～ 式(5) 分别代入到式(14) 和式(15)中计算得到电学焓的变分和外力虚功的表达式,并代入到式(16),根据变分法基本原理[35],得到纳米板的静态控制方程

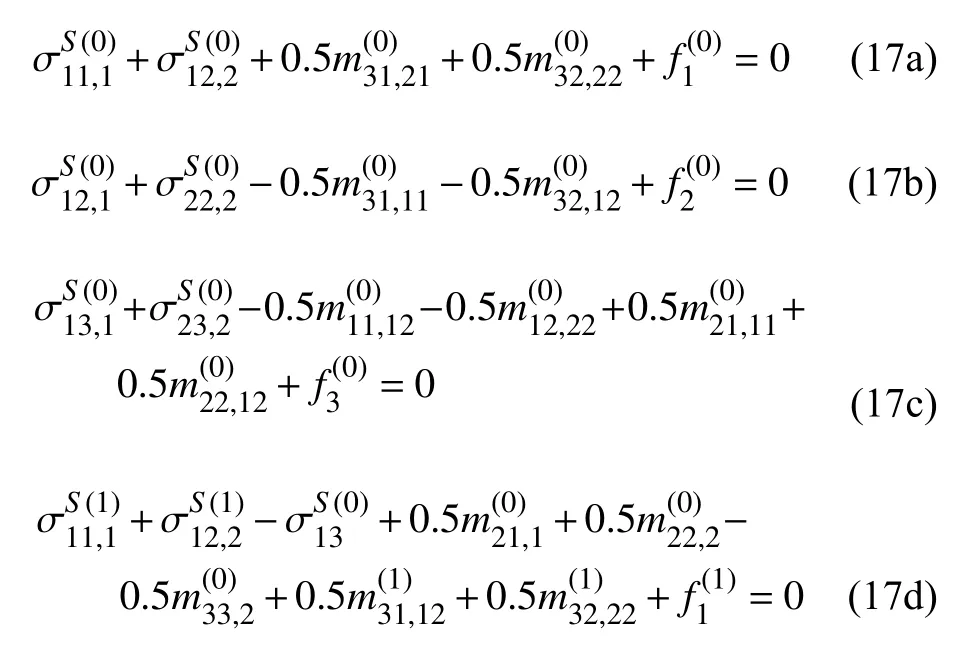
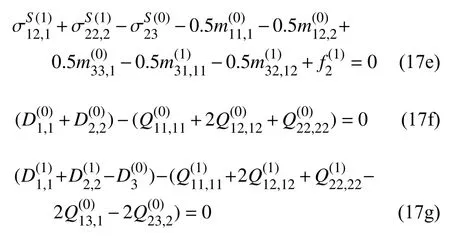
和在板边界Γ上的线积分等式

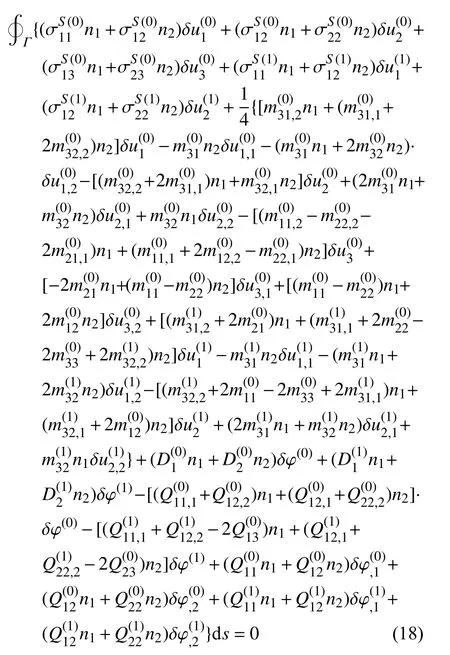
其中,Γ表示矩形板的边界,n1和n2为边界外法线的方向余弦.

1.4 四边简支矩形板的边界条件

四边简支矩形板的边界条件可以由板边界上的线积分等式(18)得到,注意到式(18)的变分项 δ(·)中,关于位移或者电势的切向导数不与其法向导数独立,因此需要进一步处理变分项 δ (·) 中包含切向导数的项.如图2 所示矩形板,其四边分别用L1,L2,L3和L4来表示,板四边的外法线的方向余弦分别为:L1边的方向余弦为n=(0,−1);L2边的方向余弦为n=(1,0);L3边的方向余弦为n=(0,1);L4边的方向余弦为n=(−1,0).将四边的方向余弦代入到式(18),根据变分法基本原理,得到矩形板完整的边界条件.

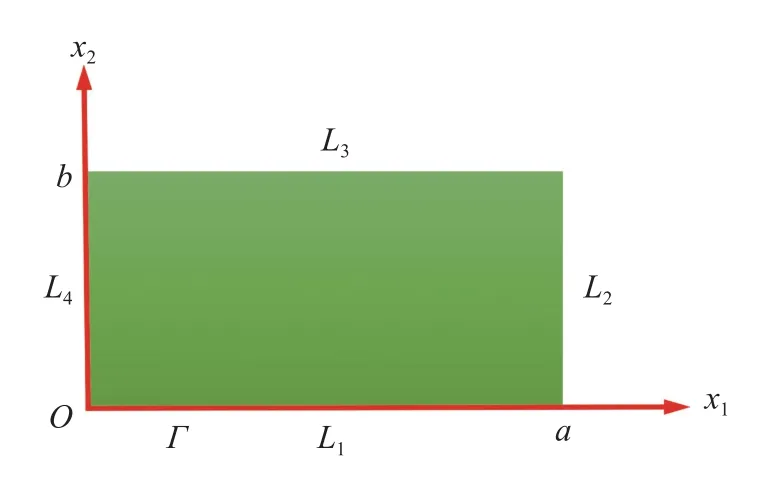
图2 四边简支板的边界Fig.2 Boundary of a simply supported rectangular plate on four sides

对于L1,L3边,边界条件为

对于L1和L3边,边界条件为

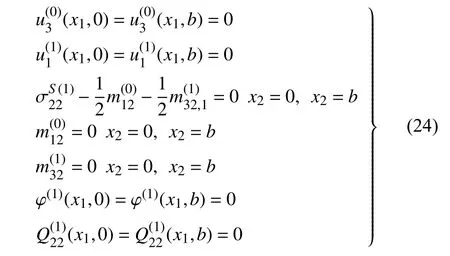
对于L2和L4边,边界条件为

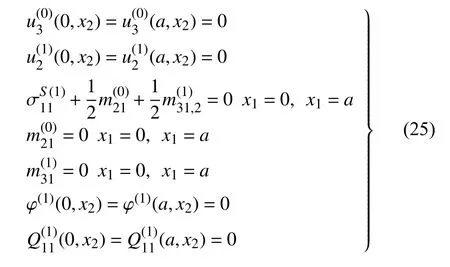
2 算例分析

根据得到的四边简支矩形板的高阶弯曲方程式(20a)～ 式(20c)、高阶电势方程式(20d)和相应的边界条件式(24)和式(25),求解纳米板的电势场,分析电场梯度对于板内电势的影响.图3 为四边简支纳米板受作用在板中心处的横向集中载荷P,直角坐标系建立在板的中面上,板的长宽分别为a和b,厚为2h.

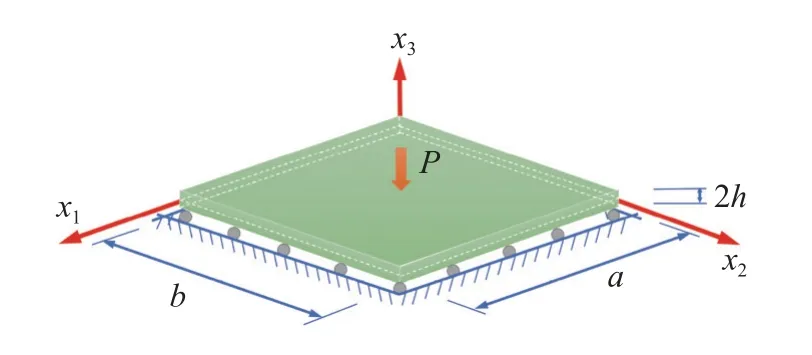
图3 四边简支矩形板受集中载荷P 作用Fig.3 Four-sided simply supported rectangular plate subjected to concentrated loading P

将满足边界条件的Navier 解代入控制方程式(20a)～式(20d)中,有

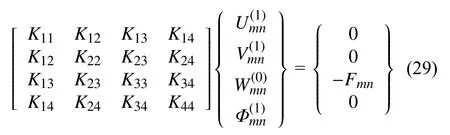
其中,系数矩阵K的分量为

算例计算中,取纳米板的材料为Si,相应的材料参数为[19,36]:C11=165.7GPa,C12=63.9GPa,C44=79.56GPa,ε11=1.035×10−10C2/(N·m2),f16=4.0×10−10C/m,g11=g12=g44=9.0×10−22C·m/V.板的几何参数为:厚2h=2×10nm,长a=40h,宽b=40h.横向集中载荷的大小为P=0.01 N.

数值计算结果表明,当级数求和项数m和n取较大值时(m>100,n>100),一阶电势φ(1)的结果与m=100,n=100时的结果相同,这说明对于和φ(1)的傅里叶级数展开式,在该问题下求和项数取m=100,n=100是足够精确的,能够保证结果收敛.

图4给出了考虑挠曲电效应和电场梯度效应的四边简支纳米板在弯曲时的一阶电势分布,板的一阶电势φ(1)在横向集中载荷施加处值最大,随着远离横向集中载荷的作用点,一阶电势φ(1)逐渐减小,在板的边界处一阶电势φ(1)为0.由于电势场φ(x1,x2,x3)=x3φ(1)(x1,x2)(见式(1)4),当在板的上表面出现电势垒时,在板的下表面出现电势阱.

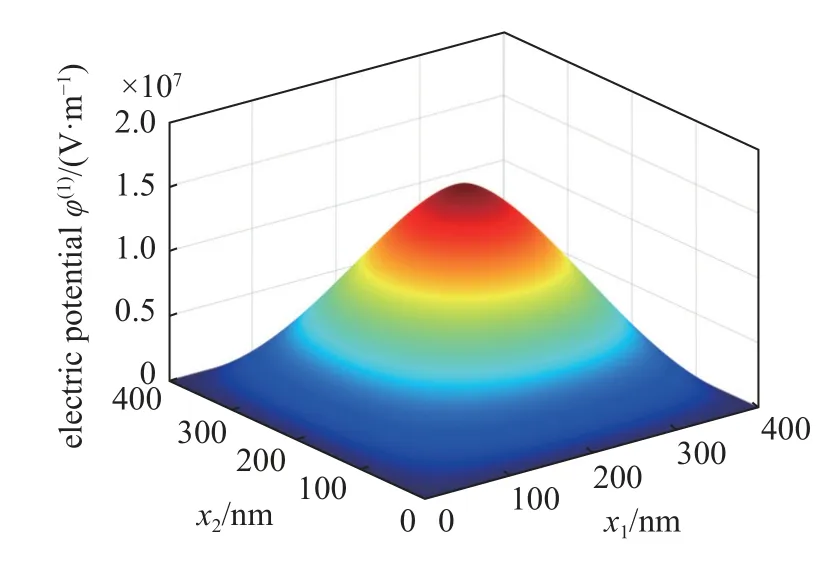
图4 四边简支矩形板的一阶电势φ(1)分布Fig.4 First-order electric potential φ(1) of the four-sided simply supported Mindlin plate

为了分析与电场梯度效应相关的材料参数gpq(gijkl的Vogit 符号表示形式)对纳米板一阶电势的影响,取g11=g12=g44,在其余条件不变的情况下,分别取g11的值为[37]9.0×10−22C·m/V,2.5×10−21C·m/V 和4.9×10−21C·m/V,计算Mindlin 板在x2=b/2处的一阶电势分布,计算结果如图5所示.从图5可以看出,随着材料参数g11的增大,矩形板在x2=b/2上的一阶电势整体上减小,这表明电场梯度的增大削弱了纳米板中由挠曲电效应产生的一阶电势.需要注意的是当不考虑电场梯度时,纳米板中心作用横向集中载荷会使一阶电势的结果出现奇异性,即随着m和n的不断增大,一阶电势的值整体上会越来越大,而电场梯度的存在则消除了当横向集中载荷作用在板中心时所引起的一阶电势的奇异性[37].

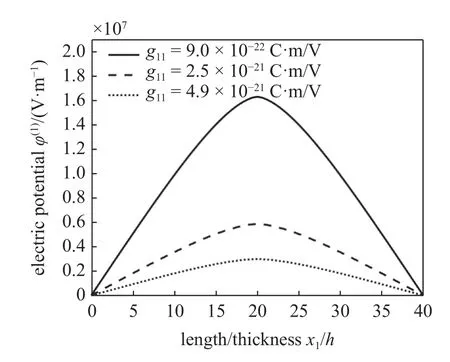
图5 不同的材料参数g11对四边简支矩形板在x2=b/2处的一阶电势的影响Fig.5 Influencesof different material parameters g11on the first-order electric potential of four-sided simply supported plateat x2=b/2

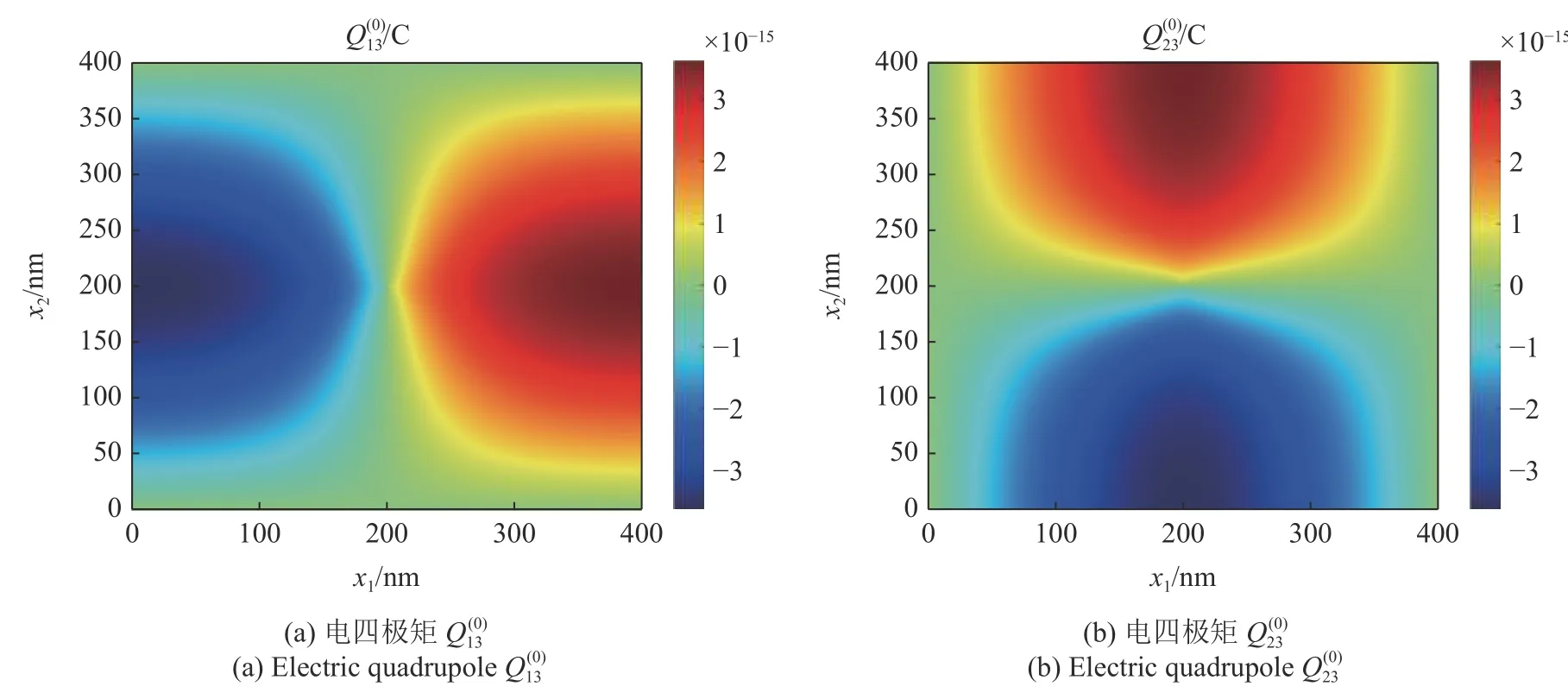
图6 四边简支矩形板的电四极矩分量云图Fig.6 Higher-order electric quadrupoleof four-sided simply supported Mindlin plate

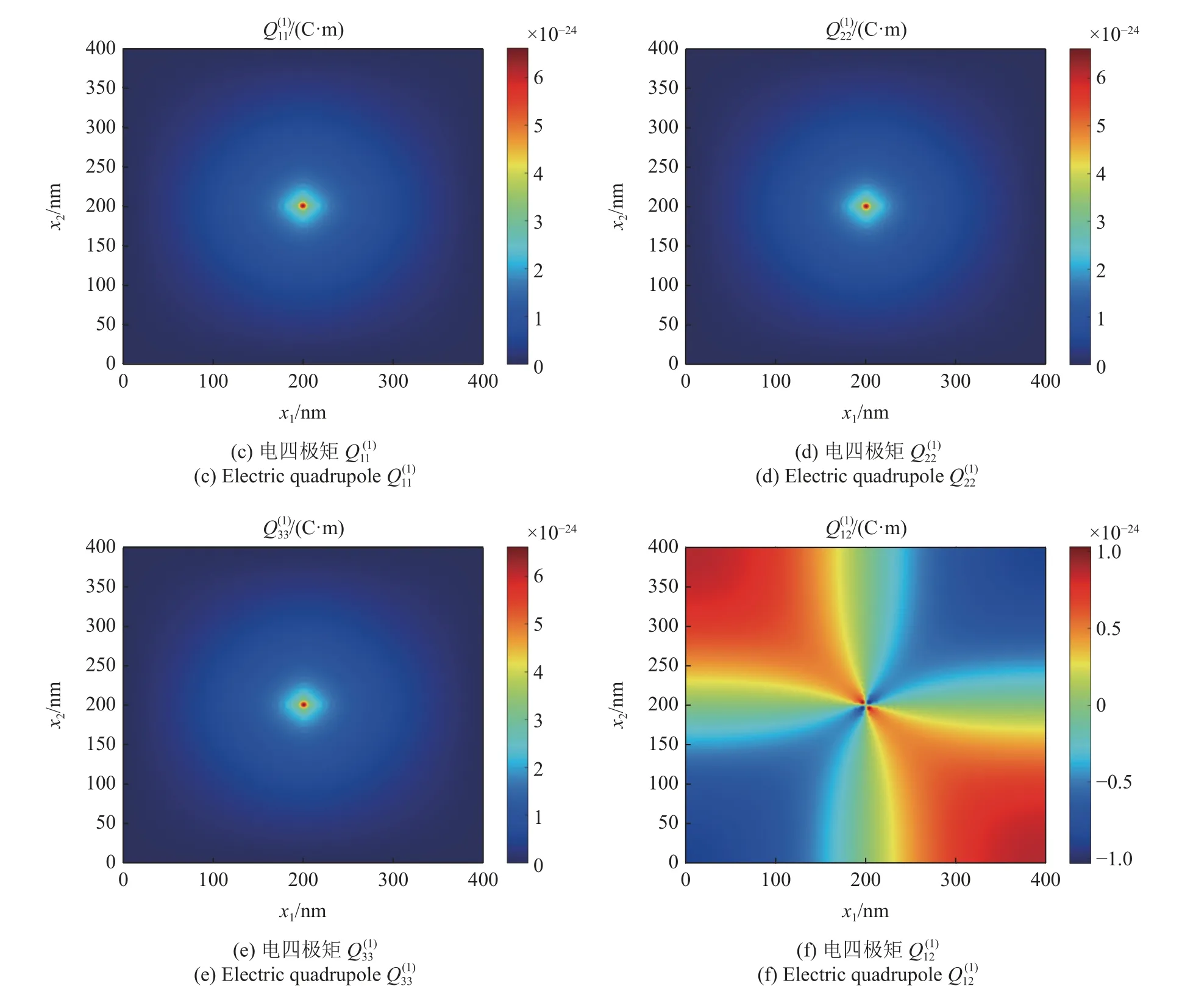
图6 四边简支矩形板的电四极矩分量云图(续)Fig.6 Higher-order electric quadrupole of four-sided simply supported Mindlin plate (continued)

3 结论

本文基于文献[23]提出的弹性介电材料的非经典理论,建立了一个考虑挠曲电效应和电场梯度效应的纳米矩形板新模型.根据Mindlin 假设给出板位移场和电势场的一阶截断表达式,基于此推导出应变、曲率、电场和电四极矩的表达式.选取立方晶体(m3m 点群)作为弹性介电材料,将相应的广义三维本构方程代入到高阶应力、高阶偶应力、高阶电位移和高阶电四极矩的表达式得到二维本构方程,利用弹性电介质变分原理得到纳米矩形板的控制方程和板边界上的线积分等式,将二维本构方程代入控制方程推导出以基本未知量表示的板的高阶弯曲方程和高阶电势方程;将纳米矩形板边界上外法线的方向余弦代入线积分等式,得到四边简支矩形板的边界条件.利用得到的四边简支矩形板的控制方程和边界条件,根据Navier 解理论,求解纳米板的电势场,重点分析电场梯度对板内电势的影响,得到以下结论.

(1)对于考虑挠曲电效应和电场梯度效应的纳米板的静态弯曲问题,数值结果表明,当考虑电场梯度效应时,随着材料参数g11的增大,矩形板在x2=b/2 上的一阶电势整体上减小,这表明电场梯度的增大可以削弱纳米板中由挠曲电效应产生的一阶电势.

(2) 当考虑电场梯度效应时,可以消除在纳米板上施加横向集中载荷时产生的一阶电势奇异性.

本文的工作是对具有挠曲电效应和电场梯度效应的微板结构分析理论的一个扩展,并且为微纳米尺寸器件的结构设计提供帮助.