钙钛矿超晶格SrTiO3/BaTiO3 的挠曲电效应*
2022-10-27陈许敏叶盼王继光霍德璇曹东兴
陈许敏 叶盼 王继光 霍德璇 曹东兴
1) (杭州电子科技大学理学院,杭州 310018)
2) (杭州电子科技大学电子信息学院,杭州 310018)
3) (杭州电子科技大学材料与环境工程院,杭州 310018)
4) (北京工业大学材料与制造学部,北京 100124)
挠曲电效应是应变梯度与电极化之间的机电耦合,存在尺寸效应,在许多微纳米尺寸结构中起着非常重要的作用.本文采用密度泛函理论,对交错层SrTiO3/BaTiO3 超晶格进行了系统的挠曲电效应研究,通过探究超晶格在给定的应变梯度下的力电响应,独立得到其纵向挠曲电系数、横向挠曲电系数和剪切挠曲电系数.结果表明: 超晶格的横向、剪切挠曲电系数和纵向挠曲电系数较其组分材料有不同的变化,其中超晶格的横向和剪切挠曲电系数分量分别较块体BaTiO3 提升约6 倍,较块体SrTiO3 提升4.2 倍和1.3 倍;纵向挠曲电系数较其组成材料基本不变;这种挠曲电系数分量不同程度提升的综合效果能够使超晶格SrTiO3/BaTiO3 较其单一组分材料的挠曲电效应产生数倍提升.本文对寻找性能优异的复合挠曲电材料具有一定理论指导意义.
1 引言
钙钛矿结构过渡金属氧化物具有广泛的物理特性,如铁电性、铁磁性、高温超导和巨磁阻性等,是凝聚态物理和材料科学研究的热点[1,2].应变梯度能够破坏晶体的反演对称性从而在材料中引起电极化,即挠曲电效应[3,4].挠曲电效应是材料应变梯度与电极化之间的耦合,不受材料对称性和铁电材料居里温度等限制,仅依赖于材料的尺寸特征[5],在许多微纳米尺寸结构中挠曲电效应对材料性质发挥主导作用[6].随着对微纳米材料的深入研究,ABO3型钙钛矿材料在小尺寸状态下表现的挠曲电效应增强逐渐吸引了学者广泛的关注[7].Lu等[8]通过原子力显微镜尖端在BaTiO3超薄膜中产生应力梯度来调节挠曲电极化,实现了采用纯机械力动态切换控制极化.Wen等[9]提出了基于铁基驻极体的挠曲电性驻极体,发现施加非均匀变形的情况下挠曲电性驻极体表现出巨大的挠曲电响应.
钙钛矿材料中存在多种可能影响挠曲电效应的因素,如内部微应变[10]、极性纳米区域[11]和表面压电性[12]等,都能很容易地对电极化产生影响,从而耦合到挠曲电效应中.表面压电性的研究表明,表面/界面工程可能是控制和增强SrTiO3等材料的挠曲电性能的可行途径[12].Zhang等[13]研究揭示了表面自发极化可能在块体的铁电材料中与挠曲电极化耦合,导致实验上高估的挠曲电效应.因此,在实验上测量所得到的挠曲电系数通常是多种因素的竞争组合结果.Zhang等[14]研究发现,LaAlO3/SrTiO3异质结以及Nb 掺杂的LaAlO3/SrTiO3异质结的挠曲电系数比LaAlO3,SrTiO3块体单晶材料提升了若干数量级,并利用挠曲电效应在LaAlO3/SrTiO3的异质结构的界面实现调节材料的电子输运性质.
利用异质界面引起的电荷、轨道、自旋以及晶格失配等自由度的重组逐渐成为调节材料电子结构的有力手段[15].氧化物超晶格将具有不同性质的材料耦合在一起,在氧化物超晶格中产生大量界面,放大了界面效应的可能性,从而影响超晶格应变下的电荷响应.Shu等[16]研究表明复合材料比一般块体材料更容易存在显著的挠曲电效应.随着氧化物薄膜制备技术的飞速发展,制备具有原子尺度的钙钛矿过渡金属氧化物超晶格成为现实[17].理论方面,学者们详细研究了单晶材料的纵向、横向和剪切挠曲电系数,包括BaTiO3和PbTiO3单晶材料的纵向挠曲电系数[18,19]和二者的横向和剪切挠曲电系数[20];而超晶格材料的理论计算仅限于纵向挠曲电系数,如1SrTiO3/1PbTiO3(SPT)[15].目前,对钙钛矿超晶格材料的扰曲电效应综合研究很少报道.本文通过构建由SrTiO3和BaTiO3以1∶1 的比例逐层交替的1SrTiO3/1BaTiO3(SBT)层状超晶格材料,增加界面效应,采用第一性原理密度泛函理论 (density functional theory,DFT),研究超晶格在应变梯度下的极化响应,系统地计算和分析该超晶格材料的扰曲电效应,包括纵向挠曲电系数、横向挠曲电系数和剪切挠曲电系数.为制备具有优异挠曲电性能的钙钛矿过渡金属氧化物超晶格材料提供理论依据.
2 计算方法
本文采用基于DFT[21]的第一性原理计算软件VASP(Viennaab initiosimulation package)[22],交换关联势使用广义梯度近似 (generalized gradient approximation,GGA)的Perdew-Burke-Ernzerhof (PBE)泛函,电子-离子交换关联作用采用投影缀加平面波势处理[23],电子平面波函数截止能量为500 eV,自洽场迭代的能量收敛标准为1×10—5eV.布里渊区积分时,采用 Monkhorst-Pack的k网格[24],计算纵向和剪切扰曲电系数时采用6×6×1,计算横向挠曲电系数时采用1×6×1.
挠曲电效应描述由四阶张量相关的应变梯度引起的极化响应:
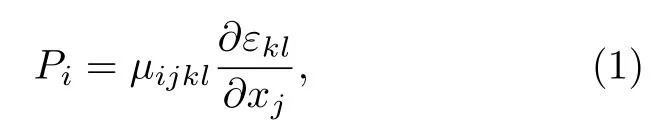
式中,Pi为挠曲电诱导的极化强度,为应变梯度,µijkl为挠曲电张量系数.根据挠曲电效应的定义可知,通过构造一个具有已知应变梯度的系统,然后计算由应变梯度诱导的极化强度,可以得到该体系的挠曲电系数.晶胞的极化强度是零电场条件下由应变梯度导致的原子位移极化,极化强度由玻恩有效电荷、晶胞体积和晶格中原子的相对位移决定:
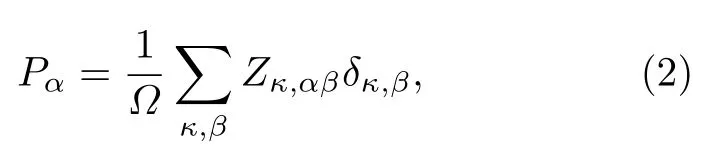
其中,Pα是沿着α方向的自发极化,Ω表示晶胞体积,Zκ,αβ是材料中原子的玻恩有效电荷,δκ,β是原子相对于中心对称结构晶格的位移.
SrTiO3和 BaTiO3晶格参数如表1,超晶格系统模拟为SrTiO3和 BaTiO3交替生长的层状材料,系统呈现1/1 层状.计算模拟超晶格系统在SrTiO3衬底上沿(001)方向生长,因此,超晶格采用了 SrTiO3的面内晶格常数,并对超晶格的c/a进行了系统优化.
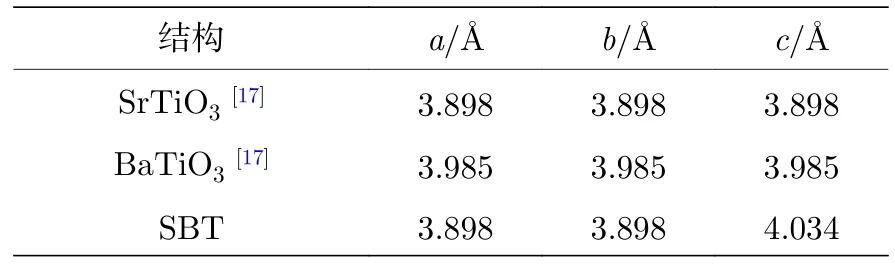
表1 结构晶格常数Table 1.Structural lattice constant.
3 计算结果与分析
3.1 纵向挠曲电系数
纵向挠曲电极化是z方向的应变梯度所引起的该方向上的极化,该极化和应变梯度的耦合关系式为
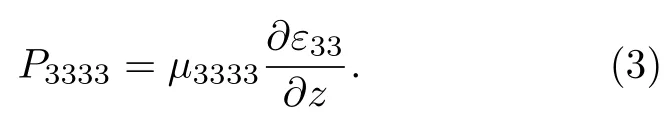
P3333是z方向的极化,∂ε33/∂z表示沿z方向的应变梯度,µ3333表示纵向挠曲电系数.图1 给出了1×1×N(N为晶胞层数)纵向挠曲电超晶胞模型.图1(a)是SrTiO3/BaTiO3的无应变超晶胞结构,该超晶胞模拟BaTiO3生长在基底为SrTiO3交替层排列的情形.考虑对图1(a)所示的超晶胞结构施加沿Z方向周期性的应变:
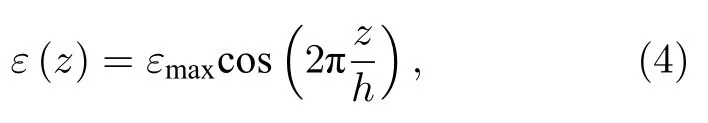
其中ε(z) 表示坐标z处的应变值,h为超晶胞Z方向高度,εmax为最大应变.超晶胞原子沿Z方向的位移为
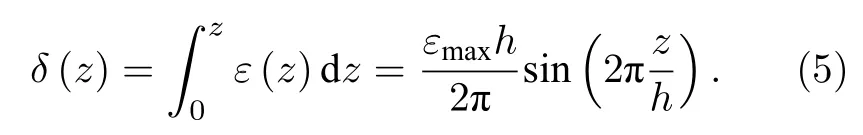
将(5)式形式的原子位移施加在图1(a)所示的超晶胞结构中,即得到图1(b)示意的内含应变梯度的SBT 超晶胞模型,晶胞内材料的应变梯度为
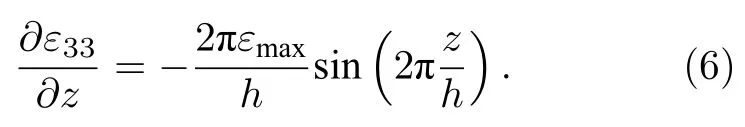
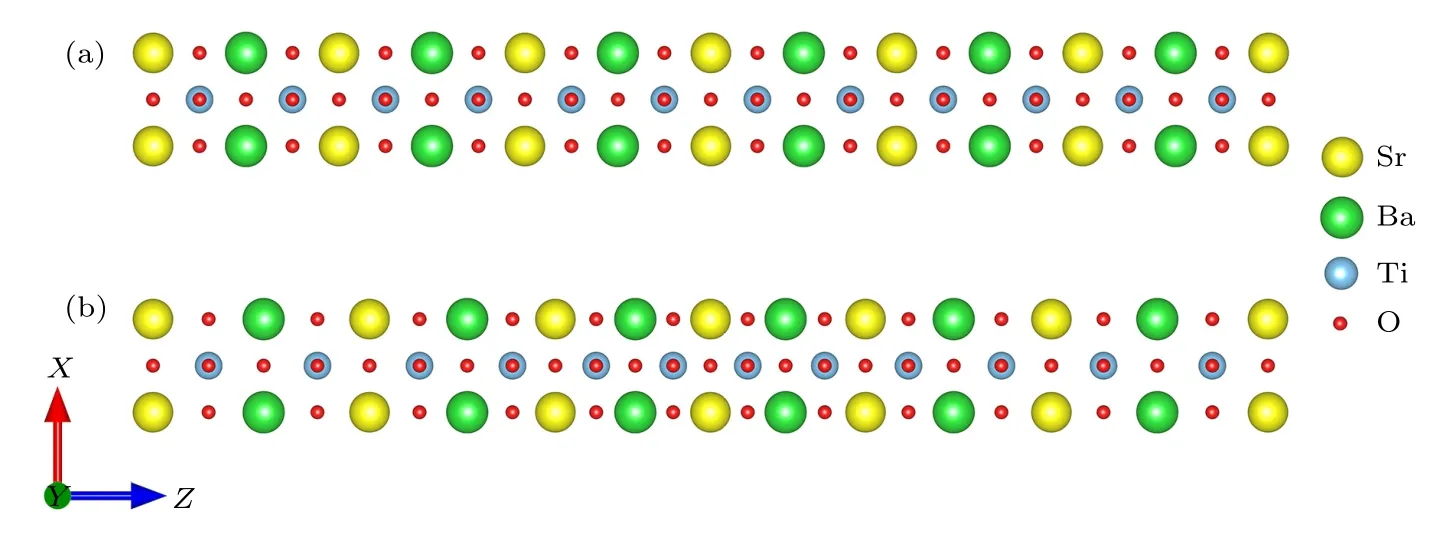
图1 1×1×N 纵向挠曲电超晶胞模型 (a) 无应变;(b) 施加纵向应变Fig.1.1×1×N supercell model for longitudinal flexoelectricity: (a) Strain-free supercell;(b) supercell with longitudinal strain.
因此,建立了SBT 超晶格与应变梯度保持相同周期性的计算模型,如图1(b)所示,在图1(b)中余弦形式的应变分布使得h/4 和3h/4 位置的平均应变为零,压电极化为零,消除了压电效应对极化的贡献,同时该位置晶胞的应变梯度最大,对应的挠曲电效应最大,可以提供最大的挠曲电极化.
为了使图1(b)所示的超晶胞维持应变梯度的状态,在施加应变ε33后,固定A位原子(Sr 或Ba)的位置,弛豫Ti 和O 原子到它们的平衡位置.对应变结构进行优化后,检查未固定的原子位置,以查看松弛的超晶胞中是否仍然存在梯度应变.图2 显示了Z方向不同高度的超晶胞在εmax=0.5%情况下原子位移的分布情况,图2(a)—(d)对应的晶胞层数N分别为12,16,20,24.图2 表明弛豫后超晶胞中的余弦应变梯度仍然存在.通过图2(a)可以看出,弛豫原子的位移比固定A位原子的位移小,意味着松弛原子的应变梯度小于预设的固定A位原子的应变梯度.而挠曲电系数由位移极化和应变梯度的比值得到,所以较小的梯度会导致高估的挠曲电系数.固定原子和弛豫原子的位移之间的差异在很大程度上是与超晶胞尺寸有关.图2(b)—(d)显示,随着超晶胞尺寸逐渐变大,弛豫原子的应变梯度和受约束的A位原子的应变梯度之间的差异逐渐减小.图2(c),(d)中显示的超晶胞中原子间的应变梯度差异几乎消失.间接表明,为了施加应变梯度而选择约束A位原子是可靠的.这表明模拟计算时超晶胞的尺寸是影响挠曲电系数的一个重要原因.由此推测,随着超晶胞尺寸的增大,晶格中固定原子和弛豫原子的应变梯度最终趋于一致,由N=24 情况下可以得到SrTiO3/BaTiO3超晶格的纵向挠曲电系数µ3333为—0.308 nC/m.

图2 1×1×N 超晶胞中A 位原子和Ti,O 原子Z 方向的位移 (a) N=12;(b) N=16;(c) N=20;(d) N=24Fig.2.Atomic displacement along z direction in 1×1×N supercell: (a) N=12;(b) N=16;(c) N=20;(d) N=24.
3.2 横向挠曲电系数计算模型
横向挠曲电效应是X方向的应变引起沿Z方向上的极化,该极化和应变梯度的耦合关系式为
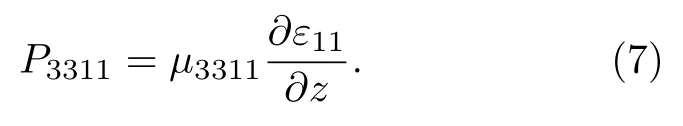
为了计算横向挠曲电系数,构造了图3(a)所示的M×1×N的超晶胞,M为超晶胞X方向的尺寸.为模拟计算横向挠曲电效应,对图3(a)中的超晶胞两侧对称施加应变形式.如图3(b)所示,该应变在X方向上关于蓝色虚线轴对称对称分布,沿Z方向呈余弦式变化,且在X方向越靠近对称轴,余弦形式的应变幅值越小,在对称轴处为零,该应变表达式为

(8)式对应的原子位移表达式为
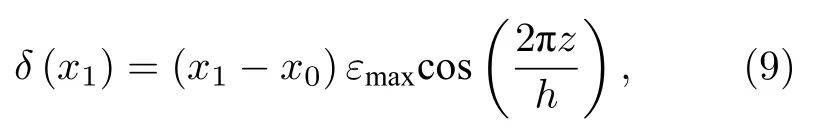
δ(x1)表示坐标为x1的原子在X方向的水平位移,x0表示图3(b)所示的蓝色对称轴沿X方向的坐标.图3(b)中超晶胞的应变梯度为

分析(8)式和(10)式可知,应变和应变梯度在Z方向上呈周期性,并且与超晶胞的周期一致.因此,横向挠曲电效应引起的极化分布在Z方向也是周期性的且在边界处连续,从而可以减小退极化场的影响.为了保持弛豫前后晶胞单元在X方向上的总长度不变,固定超晶胞两侧边缘的原子,以保持超晶胞体积保持不变.

图3 M×1×N 的横向挠曲电超晶胞模型 (a) 无应变;(b) 施加横向应变Fig.3.M×1×N supercell model for transverse flexoelectricity: (a) Strain-free supercell;(b) supercell with transverse strain.
为保持图3(b)所示超晶胞内的应变,在施加应变ε11(z) 后,固定Ba,Sr 原子在X方向的坐标,但允许在其他两个方向弛豫;Ti 原子和O 原子不受约束,可以在各个方向弛豫.结构优化后,超晶胞Y方向上的原子没有发生应变,即ε22=0.对Z方向的晶胞没有限制,表明晶胞中原子可以在Z方向上自由弛豫.原子弛豫到它们的平衡位置时,(10)式的应变梯度仍然存在于超晶胞中内部.选取超晶胞中对称轴上的晶胞来考虑挠曲电系数,因为此处的晶胞受水平方向上对称的应变,能消除水平退极化场的影响.对于SrTiO3/BaTiO3超晶格,极化也可能通过压电效应产生,为了准确计算横向挠曲电系数,需尽可能消除压电效应的影响.根据(8)式,位于超晶胞中间列h/4 和3h/4 位置的晶胞水平应变为零,不受压电效应的影响,同时从(10)式可知,此处的应变梯度最大,挠曲电效应最大.因此,选择超晶胞中间列h/4 和3h/4 处的晶胞来计算横向挠曲电极化强度,不仅可以消除压电贡献,而且由于其最大的应变梯度而具有最大的挠曲电性.
对施加了应变的M×1×N超晶胞进行结构优化,最大应变设置为εmax=0.5%.经过测试,为维持超晶胞应变梯度的存在,设置M=7 比较合适.图4(a)—(c)是超晶胞在不同纵向尺寸下的原子水平位移,在Z方向上单胞层数分别为N=8,12,16.图4 显示了超晶胞结构优化后O 原子弛豫到趋于固定原子的应变状态,证明了结构优化后的超晶胞处于应变梯度状态.
从图4(a)可以看出,弛豫后晶胞内O 原子的位移分布呈余弦形式,但与固定A位原子的位移差异明显.随着超晶胞纵向尺寸的增加,图4(b)中的固定原子和非固定原子之间的差异进一步减小.图4(c)中O 原子的位移曲线几乎收敛到与Ba/Sr的位移曲线相一致.在h/4 和3h/4 的特定位置,Sr/Ba 原子位移曲线和O 原子的位移曲线相交且Z方向的位移基本为0,如图4(c)中的第4 个和第5 个红点(从左到右)所示.因此,如果我们选择这些特定的位置来计算超晶胞的挠曲电系数,就可以忽略压电效应的影响.由于超晶胞内周期性位移分布,以及垂直极化沿z方向的连续性,使其在超晶胞的顶部和底部边界没有退极化场,同时中间一列晶胞不受水平去极化场影响.因此,超晶胞尺寸的变化,并不会引起退极化场对挠曲电系数的影响.
图4(d)中的实线对应于图4(c)N=16 时的纵向应变分布以及挠曲电极化分布.可以看出,对超晶胞在X方向上施加的横向应变梯度,导致中间列的单晶胞在Z方向发生余弦形式的应变分布,这意味着沿Z方向存在纵向应变梯度及其诱导的纵向挠曲电极化.因此,模拟计算横向挠曲电系数时,SrTiO3/BaTiO3超晶胞的总挠曲电位移极化包括横向挠曲电极化和纵向挠曲电极化的贡献,总挠曲电极化可表示为
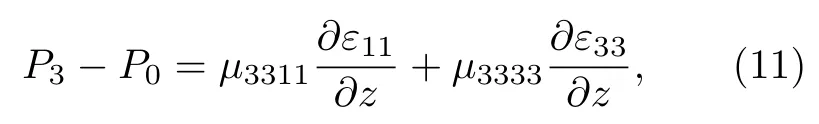
其中,P0是初始状态的自发极化,对于非铁电晶体,P0=0.(11)式中由应变梯度诱导的位移极化可以根据玻恩有效电荷计算得到.根据(11)式计算得到超晶胞中间一列的挠曲电极化情况,如图4(d)中的虚线所示,是N=16 的超晶胞的极化分布.可以看出,h/4 和3h/4 处的局部极化强度达到最大且方向相反.

图4 7 ×1×N 超晶胞中A 位原子和O 原子的Z 方向位移 (a) N=8;(b) N=12;(c) N=16;(d) N=16 超晶胞中的挠曲电极化分布和纵向应变分布Fig.4.Z displacement of A-atoms and O-atoms in 7 ×1×N supercell: (a) N=8;(b) N=12;(c) N=16;(d) the polarization and longitudinal strain along z direction with N=16.
由于挠曲电极化中包含横向挠曲电极化和纵向挠曲电极化两种成分,为了准确测量横向挠曲电系数,需要消除纵向挠曲电极化的贡献.由横向应变引起的纵向挠曲电效应可以根据纵向应变梯度和纵向挠曲电系数的耦合得到,其中纵向应变梯度可以根据图4(a)中的应变分布得到,纵向挠曲电系数由前文的计算结果得到,这里取µ3333=—0.308 nC/m.根据(11)式,横向挠曲电系数计算如下:

在图4(d)中最大挠曲电极化的位置计算得到的横向挠曲电系数µ3311=9.87 nC/m.
3.3 剪切挠曲电系数
剪切挠曲电效应指沿Z方向变化的X方向的应变引起的X方向上的极化,该极化和应变梯度的耦合关系用下式描述:
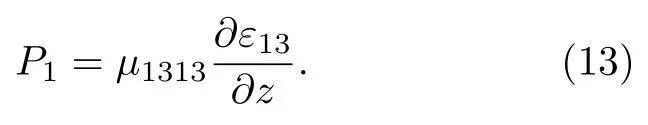
根据剪切挠曲电效应的定义构造了一个计算剪切挠曲电系数的超晶胞,如图5(a)所示,对此超晶胞施加了沿竖直方向余弦变化的水平位移,该位移表达式为
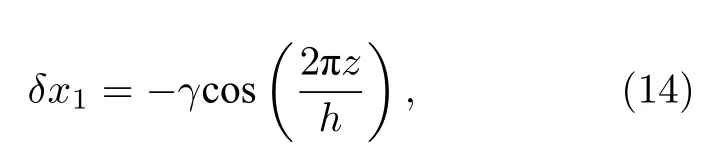
其中,γ是剪切应变的比例因子.图5(b)为施加剪切应变后的超晶胞模型,由于原子的水平位移很小,对(12)式做二阶求导得到超晶胞剪切应变梯度表达式为
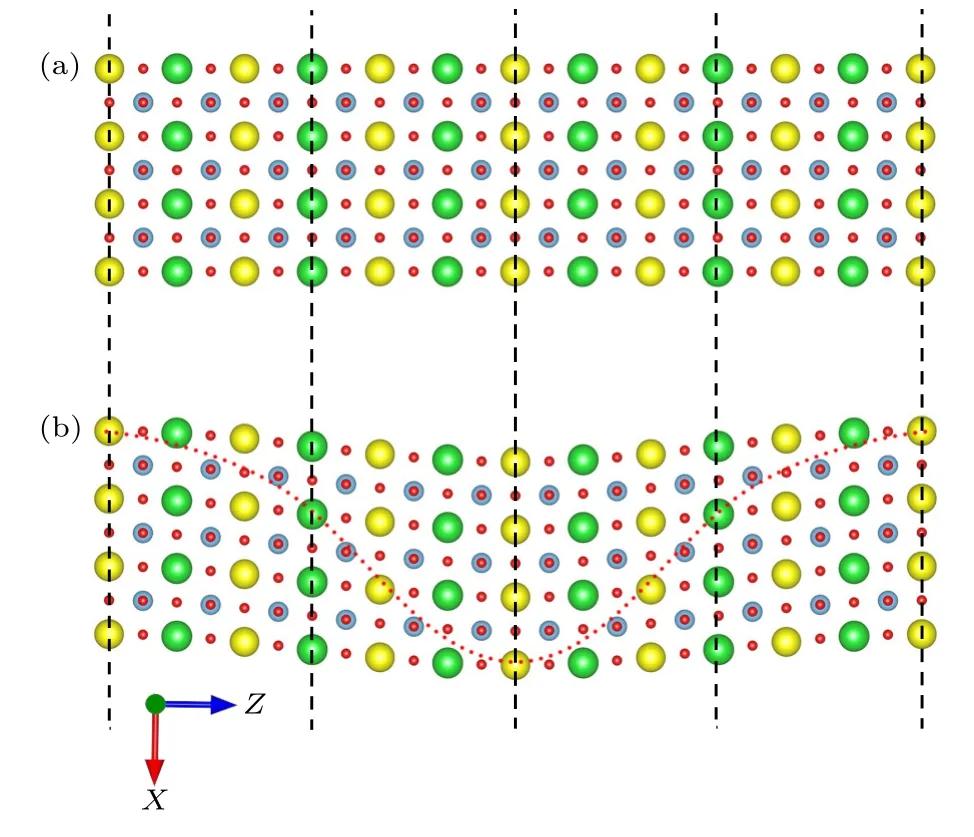
图5 M×1×N 的剪切超晶胞模型 (a) 无应变模型;(b) 施加剪切应变Fig.5.M×1×N supercell mode for shear flexoelectricity:(a) Strain-free supercell;(b) supercell with shear strain.
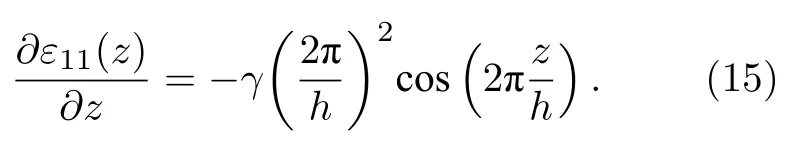
对施加剪切应变后的超晶胞进行结构弛豫,Ba/Sr原子X方向坐标在弛豫过程中固定,其他原子各方向坐标允许弛豫到其平衡位置.
为了研究超晶胞的剪切挠曲电效应,对不同纵向尺寸的剪切应变超晶胞模型进行了结构优化,剪切应变系数γ=0.3 Å (1 Å=10—10m).弛豫超晶胞结构后,考察不同尺寸的超晶胞中应变梯度是否存在.图6(a)—(c)给出了超晶胞中Sr/Ba 原子和O 原子位移的比较.结果表明,在图6(a)中,对于较小的纵向尺寸(N=12),O 原子的位移并不收敛于固定Sr 原子位置的位移.当尺寸增加到N=28时,Sr 和O 原子的位置保持一致,如图6(c)所示,这表明随着晶胞尺寸增大,结构弛豫后超晶胞内固定原子与非固定原子最终能够维持预计的应变梯度.
对于没有压电效应和自发极化材料,对极化的唯一贡献来自剪切挠曲电效应.利用玻恩有效电荷计算超晶胞中的水平挠曲电极化,图6(d)显示了N=28 的超晶胞中的水平极化随Z高度的分布.可以看出,局域极化的分布与(15)式给出的应变梯度方程具有相同形式,呈余弦形式变化.从图6(a)—(c)可以看出,h/2 晶胞位置处应变梯度最大,挠曲电效应最强,因此在h/2 晶胞位置来计算超晶格的剪切挠曲电系数.根据(13)式计算在应变梯度最大的方向上的剪切挠曲电系数µ1313,当N=28 时,µ1313=—9.02 nC·m—1.
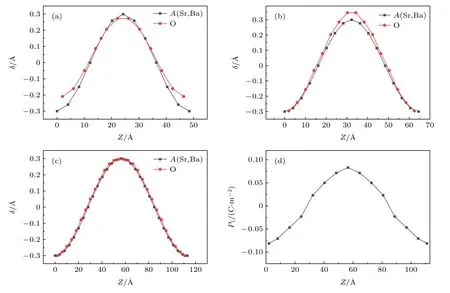
图6 3×1×N 超晶胞中A 位原子和O 原子的X 方向位移情况 (a) N=12;(b) N=16;(c) N=28;(d) N=28 超晶胞中不同高度的X 方向极化Fig.6.X displacement of A-atoms and O-atoms in 3 ×1×N supercell: (a) N=12;(b) N=16;(c) N=28;(d) X-polarization at various height inside supercell with N=28.
3.4 结果讨论与分析
表2 总结了不同块体材料和超晶格的挠曲电系数理论计算值.块体BaTiO3,SrTiO3,超晶格SBT 的横向挠曲电系数和剪切挠曲电系数均为nC/m 量级,对应的纵向挠曲电系数为次nC/m 量级.然而,SBT 超晶格的横向和剪切挠曲电系数相比于组成材料 BaTiO3和 SrTiO3都得到了数倍的增加;其中,SBT 超晶格的横向、剪切挠曲电系数分量较块体 BaTiO3提升约6 倍;较块体 SrTiO3横向和剪切挠曲电系数分别提升4.2 倍和1.3 倍.纵向、横向和剪切挠曲电系数的综合效果将决定SBT 超晶格在实验上的扰曲电性能.SBT 超晶格材料在外界的应变梯度下在竖直方向产生的挠曲电场应当表示为[8]
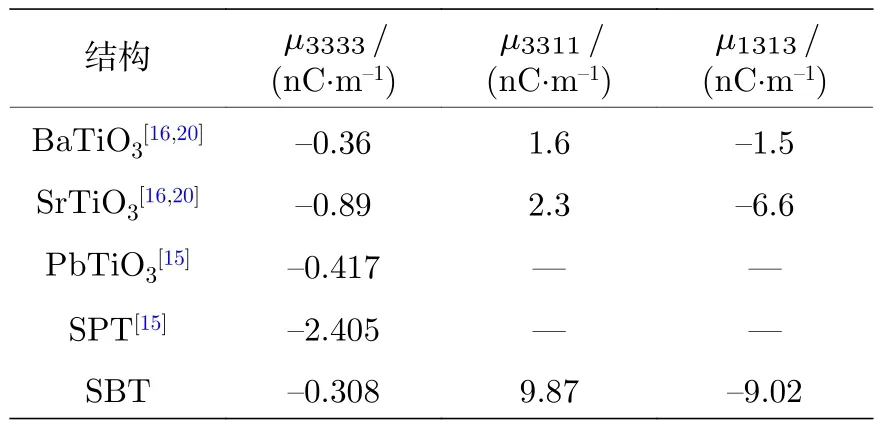
表2 挠曲电系数汇总Table 2.Summary of flexoelectric coefficient.
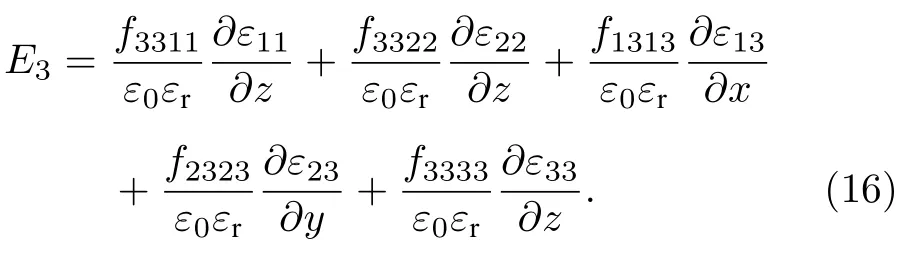
其中,E3是竖直方向的挠曲电场,ε0是真空介电常数,εr是应变下的介电常数,等号右边第一项和第二项是横向挠曲电效应的结果,第三项和第四项是剪切挠曲电效应的结果,最后一项是纵向挠曲电效应的结果.在SBT 结构中,横向和剪切挠曲电分量的增强对总体的挠曲电效应增强有显著效果.因此,SBT 超晶格理论上可以拥有数倍于块体组成材料的扰曲电性能.
SBT 超晶格的纵向挠曲电系数略微减小,与Hong[18]和Xu等[20]计算的块体钙钛矿材料 BaTiO3的挠曲电系数有相同的数量级.一方面,可能是由于 SrTiO3和 BaTiO3晶格失配影响原子在c方向的位移,导致高估的应变梯度从而低估了挠曲电系数.另一方面,可能是由于原子堆垛顺序对极化产生影响,不同的原子堆垛顺序会有不同的界面结构.Guo等[25]研究发现,在 SrTiO3/BaTiO3异质结中,TiO2-BaO 界面结构产生的界面效应会削弱纵向挠曲电极化,SrO-TiO2界面效应会增强纵向挠曲电极化,此外,不同堆垛顺序异质结构的界面结合能表现出显著差异,这种堆叠次序对纵向挠曲电极化的影响仍需进一步确认.
4 结论
超晶格钙钛矿氧化物丰富的界面行为使其可能表现出优异的挠曲电性能.本文构建了钙钛矿氧化物超晶格SBT,采用第一性原理计算了在给定的应变梯度下,超晶格中的原子位移,结合玻恩有效电荷,得到挠曲电极化与应变梯度的耦合关系,即挠曲电系数.通过构建超晶格的方式向材料中引入更多界面,显著提升了材料的横向和剪切挠曲电系数,是一种增强挠曲电效应的可靠思路,系统且全面地丰富了挠曲电效应在超晶格中的研究,为挠曲电系数的实验测量提供参考.同时,为获取较大挠曲电系数材料提供了一种可能的方法,即通过组成交错结构的超晶格材料来调节挠曲电性器件的挠曲电响应,为寻找和制备高性能的挠曲电材料提供了新思路.
