应变梯度Mindlin 板边值问题的讨论1)
2022-12-18徐晓建邓子辰
徐晓建 邓子辰 )
* (长安大学公路学院,西安 710064)
† (西北工业大学复杂系统动力学与控制工信部重点实验室,西安 710072)
引言
板壳等固体结构广泛应用于航空航天、土木、机械等领域中.随着纳米科技的不断进步,人们逐渐发现,材料/结构表现出与经典力学预测不一致的情况.具体表现在,经典力学理论模型不能准确预测弹性常数存在尺度效应的现象.基于此,人们采用试验和分子动力学两种方法对微纳米材料/结构的力学行为进行研究.但由于试验费用昂贵且分子动力学方法费力耗时,将非经典连续介质力学用于表征微纳米材料/结构的力学行为方面越来越引起国内外学者的关注[1].常见的表征材料/结构力学行为的非经典弹性理论有表征材料具有硬化效应的偶应力理论[2-4]和应变梯度理论[5],表征材料/结构的软化效应的非局部理论[6]和兼具表征材料硬化和软化效应的表面弹性理论[7].
但由于一般的非经典弹性理论含有较多表征材料参数的弹性常量,在工程应用中受到巨大挑战.因此,寻求一种非经典弹性理论一方面能够包含较少的弹性常数,另一方面能够准确预测材料/结构的尺度效应,是众多学者的一致想法.针对各向同性材料,Aifantis[8]提出了一个仅包含3 个独立弹性常数的简化应变梯度理论.该理论广泛用于梁板壳等工程结构的力学行为研究中[9-11].Papargyri-Beskou 等[12]研究了欧拉梁的弯曲和屈曲问题,并对高阶边界条件的影响做了分析.Giannakopoulo 等[13]给出了带有裂纹的悬臂梁弯曲问题的解析解.Timoshenko 梁屈曲问题的解析解及其高阶边界条件的选择对屈曲荷载的影响由文献[14]系统给出.Papargyri-Beskou 等[15]以及Niiranen 等[16]通过变分原理导出了Kirchhoff板的可能边界条件及其角点条件,并研究了高阶边界条件对板结构力学行为的影响.随后,徐晓建等[17]指出文献[15]中的不足,并利用变分原理给出了板的边值问题的新提法及其角点条件的位移形式的表达式.为精确预测碳纳米管的波传播特性,Xu 等[18]建立了圆柱壳模型,并得到与分子动力学方法相吻合的结果.Torabi 等[19]采用非线性有限元法研究了应变梯度厚板的弯曲问题.徐巍等[20]导出了Mindlin板的控制微分方程,并给出了周边简支板自由振动固有频率的解析解.在3D 应变梯度理论方面,Gao等[21]通过变分原理修正了前人给出的高阶边界条件,Polizzotto[22]给出了各向同性固体在应变梯度理论下简化的本构模型.
由以上综述可知,虽然应变梯度理论能够较好地捕捉微纳米材料/结构的力学行为,但是由于应变梯度的引入,导致系统总势能经过变分后产生高阶边界条件的问题,这给人们能否准确求解其力学边值问题带来巨大挑战.因此,开展应变梯度理论下连续介质力学模型边值问题的研究是摆在力学工作者面前不可回避的关键科学问题.
近年来,针对经典板力学行为的研究有理论解和数值解两个方面.在理论解方面,Xing 等[23]采用修正的分离变量法得到正交矩形薄板在不同边界条件下的固有频率解.徐司慧等[24]给出了黏弹性层状周期板动力学行为的近似理论与解答.周边简支Mindlin 矩形板的热弹性阻尼解析解由马航空等[25]给出.Miranda 等[26]利用数值方法、试验方法和理论分析法3 种方法研究了弹性超材料Mindlin-Reissner厚板的波传播特性.赵唯以等[27]研究了集中荷载作用下周边简支钢板-混凝土组合板的力学性能.滕兆春等[28]研究了温度对Winkler-Pasternak弹性地基多孔FGM 矩形板自由振动频率的影响.更多关于经典板理论解的研究,可参见Xing 等[29]的综述文献.在数值解方面,Niiranen 等[30]采用等几何分析(isogeometric analysis)研究了应变梯度弹性Kirchhoff 板的静挠度和自由振动问题.刘璟泽等[31]利用有限元法分析了曲线加筋Kirchhoff-Mindlin 板的自由振动问题.更多关于板的数值求解问题可参见相关文献[32].
经典Kirchhoff 板是一个4 阶偏微分方程,从数学角度来讲,只需要每个矩形边提供2 个边界条件,问题就变成适定的.但泊松却给出了3 个边界条件,显然从数学角度上来讲这3 个边界条件并不相互独立.随后,Kirchhoff 把扭矩的影响纳入到剪力中解决了这个数学矛盾.由此可见,针对板理论模型控制微分方程的阶数,给出匹配的边界条件对于板理论的发展和应用具有非常重要的理论意义和应用价值.
本文基于简化的应变梯度理论,采用变分原理,推导了Mindlin 板的控制微分方程、边界条件和角点条件,讨论了矩形板和圆形板的广义经典边界条件和非经典边界条件的表达式,以期为其有限元法和伽辽金法等数值方法的建立提供理论依据.
1 简化的应变梯度理论及Mindlin 板模型
1.1 简化的应变梯度理论
考虑一个体积为V,平面域为Ω,边界线为Γ的各向同性线弹性固体,受到体力为b、面力为t、弯矩为m、边界线力f、角点力Fc的作用.其应变能U包含经典应变能和因应变梯度引起的应变能两部分,即[33]
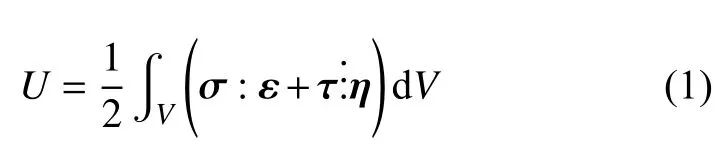
几何关系为
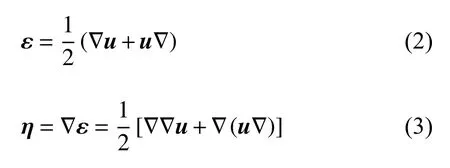
式中,σ和τ分别为2 阶普通应力张量和3 阶双应力(double stress)张量,ε和η分别为2 阶应变张量和3 阶应变梯度张量,u为位移矢量,∇ 为梯度算子.
双应力张量τ满足以下关系

式中,l2为具有长度量纲的材料尺度效应参数.
由文献[33]可知,系统外力功为
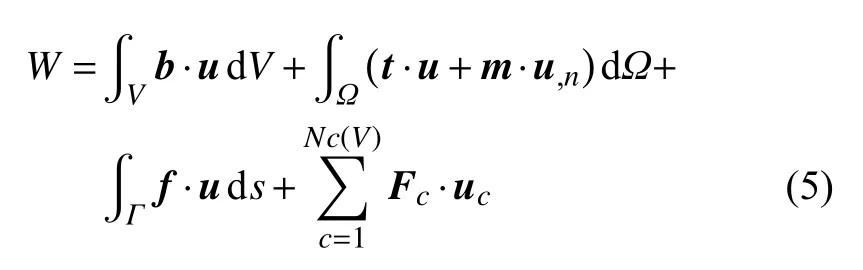
则系统总势能为
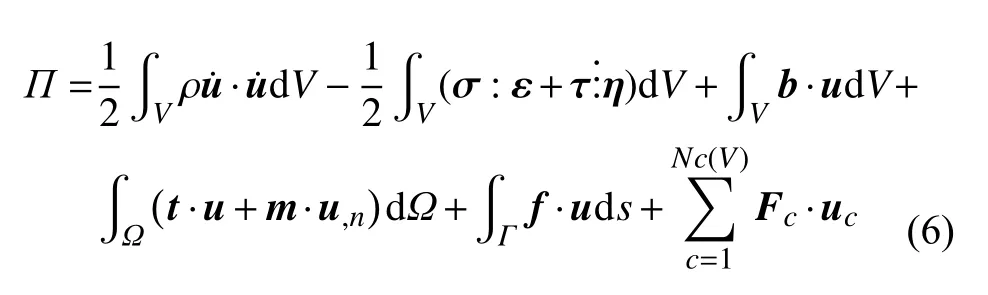
式中,ρ为体密度,上点号代表对时间的导数,n为单位外法线方向,下标逗号代表对参量的导数.
1.2 Mindlin 板方程和边界条件
考虑一体密度为ρ厚度为h的各向同性线弹性均质板,在xOy平面内占据任一形状的二维域Ω,该域边界为分段光滑曲线Γ,切线方向为s,外法向方向为n,如图1 所示.规定n到s的转向与x轴到y轴的转向符合右手螺旋时为正,并且坐标x正向和n的夹角为θ.假定薄板承受一横向分布载荷p、边界弯矩 边界力 边界扭矩 高阶边界弯矩 和高阶扭矩 的作用,横向位移为w=w(x,y,t).为后续推导方便,符号约定如下: 下标中的希腊字母代表平面坐标,下标中的拉丁字母代表空间坐标,并使用爱因斯坦求和约定.
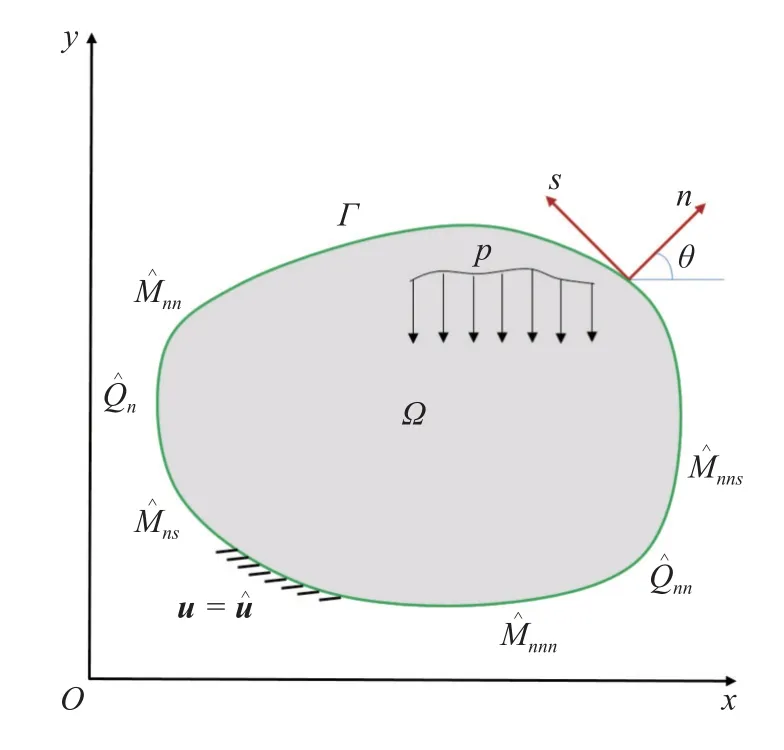
图1 Mindlin 板及其边界Fig.1 A Mindlin plate and its boundary
当不考虑面内位移的影响时,经典Mindlin 板理论的位移场为[32]
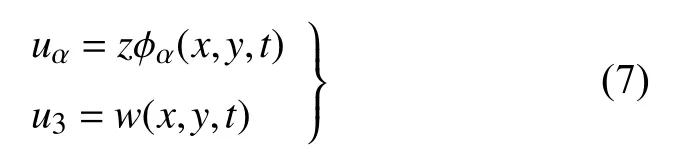
式中,ϕα为中性面沿 β(≠α) 方向的转角.
将式(7)代入到式(2),得应变为
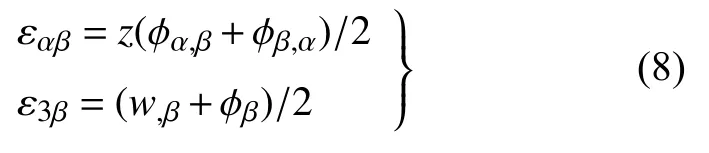
各向同性材料的本构方程为
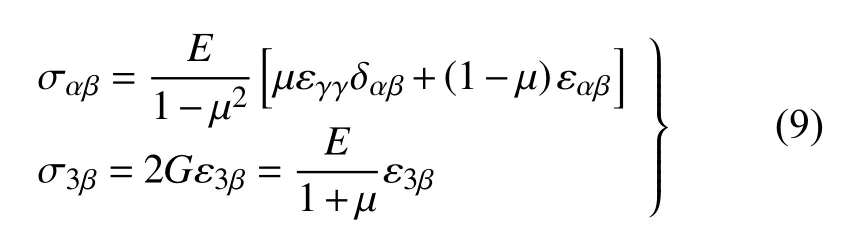
式中,E,μ和δ分别为板的弹性模量、泊松比和克罗内克δ函数.
定义弯矩和剪力分别为
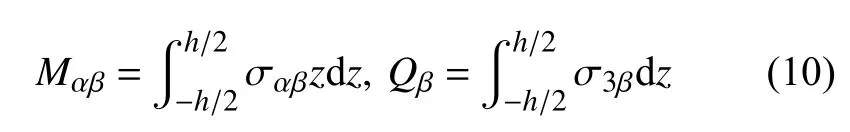
由式(8)~ 式(10)可知,弯矩和剪力与位移间的关系为
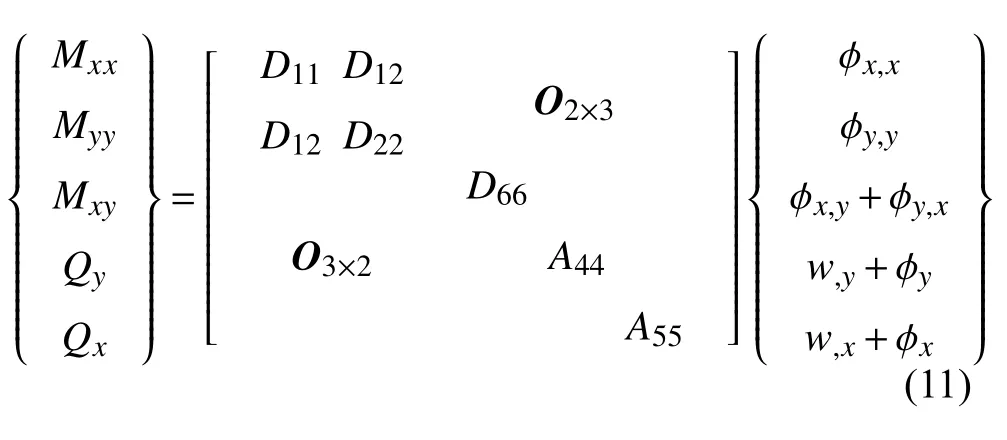
式中,κ2为剪切修正因子,且弯曲刚度为
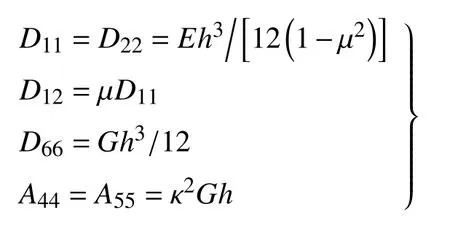
其中,G为剪切模量.
1.2.1 控制微分方程及边界条件
由式(1)可知,应变能的一阶变分为
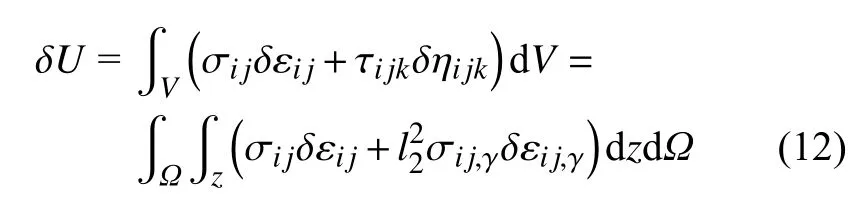
在式(12)中,忽略了对z方向的偏导数,即令角标k=γ.忽略该角标的原因如下: (1)板的平面尺寸相较于其厚度来讲较大,故而z方向的偏导数可以忽略[15-16,34];(2)本文致力于板的边值问题及角点条件研究,z方向偏导数是否考虑都不会改变其角点条件的存在性.
将式(8)代入到式(3)和式(12),并考虑到定义式(10),对得到方程的指标γ进行一次分部积分后,式(12)等价于如下形式
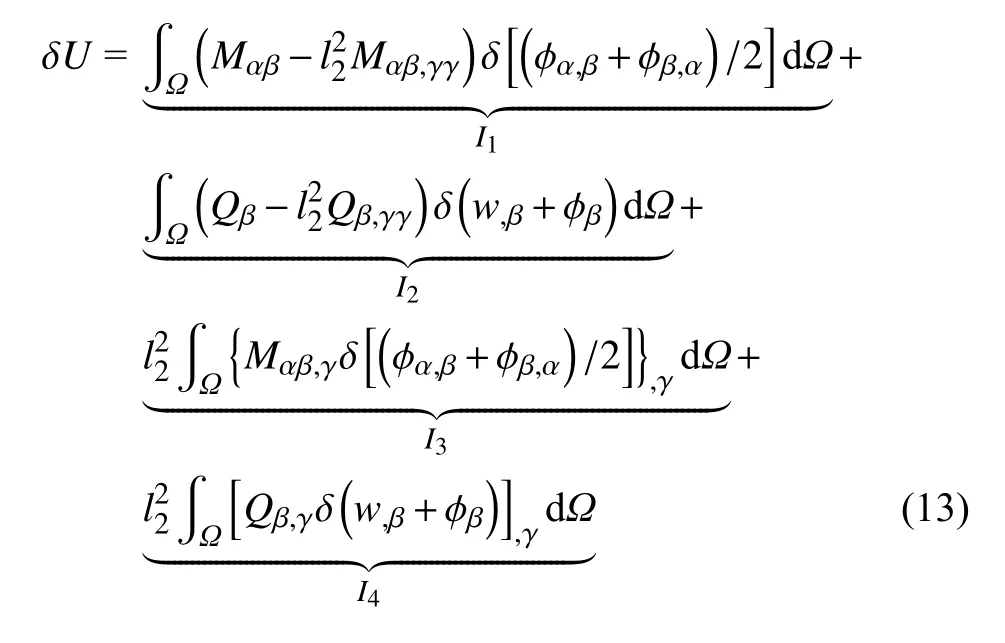
为便于计算式(13)的变分,执行以下4 步.
(1)I1的计算
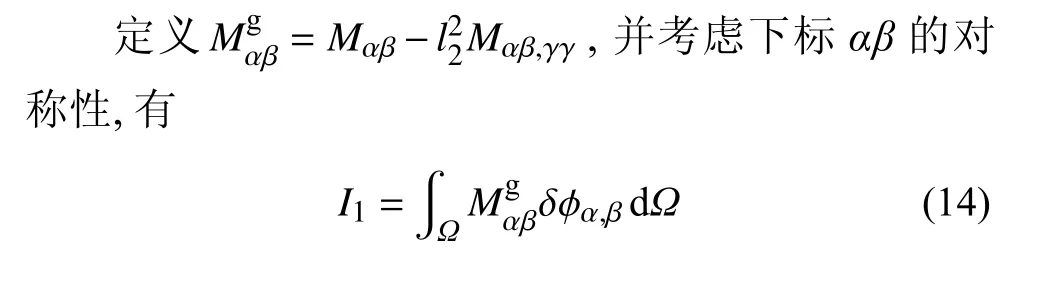
式中,上标g 为应变梯度(strain gradient)之意.
对式(14)进行一次分部积分,并利用格林定理得
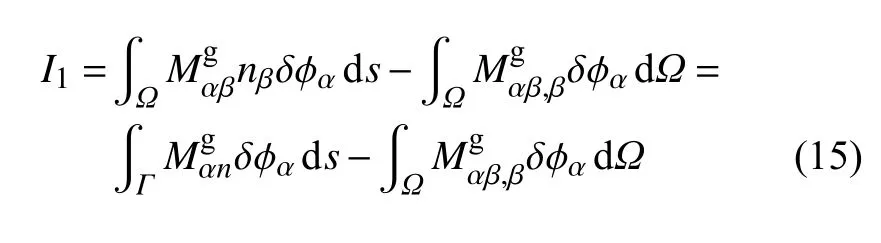
式中,第二个等式利用了直角坐标与(n,s)坐标转换关系.
(2)I2的计算
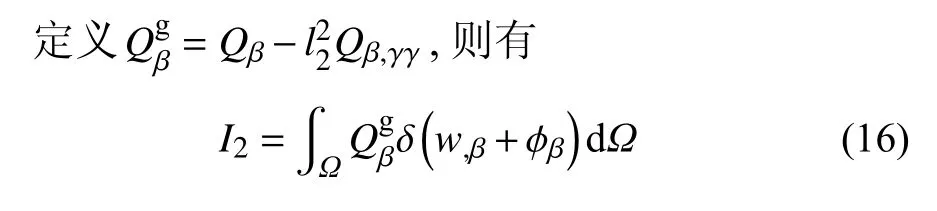
对式(16)括号内第一项进行一次分部积分和利用格林定理,经过一些符号运算,得
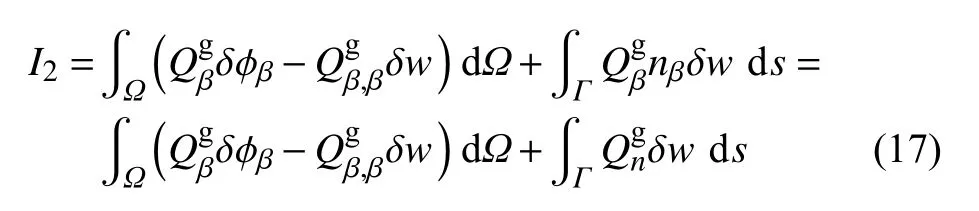
式中,第二个等式利用了直角坐标与(n,s)坐标转换关系.
(3)I3的计算
考虑到下标αβ的对称性,有
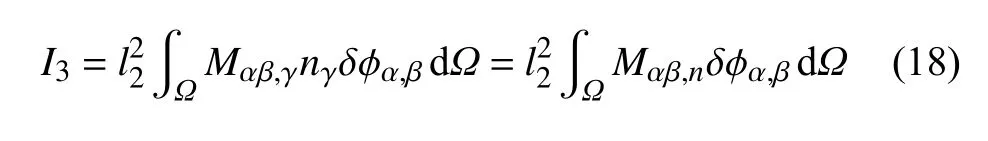
式中,第二个等式利用了直角坐标与(n,s)坐标转换关系.
将对指标β的偏导数转化为法向和切向分量,即
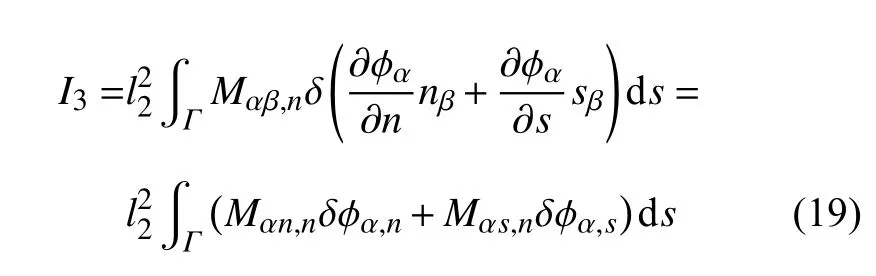
式中,第二个等式利用了直角坐标与(n,s)坐标转换关系.
对式(19) 第二个等式第二项进行一次分部积分,有

式中,最后一项为角点条件.
(4)I4的计算
利用格林定理,得
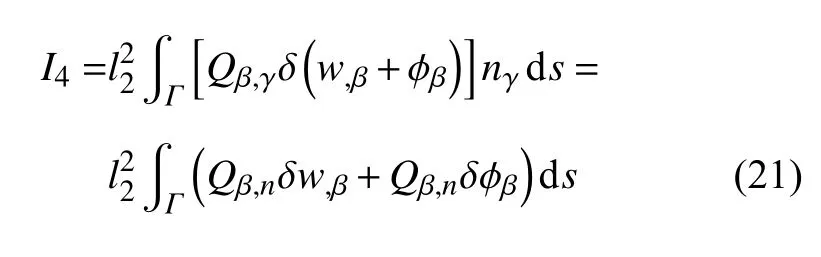
式中,第二个等式利用了直角坐标与(n,s)坐标转换关系.
式(21)第二个等号右端第一项转化为法向和切向分量,得
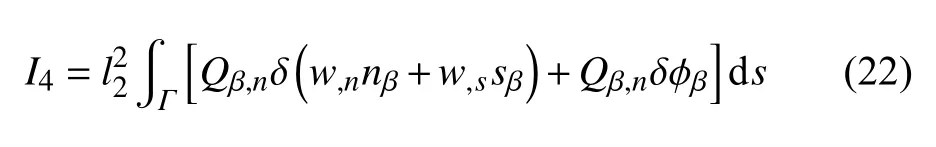
对式(22)第二项进行一次分部积分,得
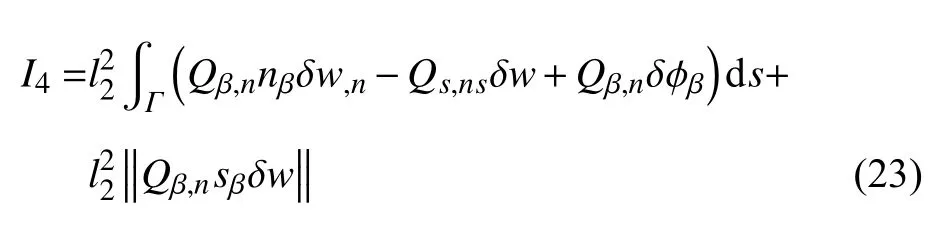
式中,最后一项为角点条件.
系统的外力功为
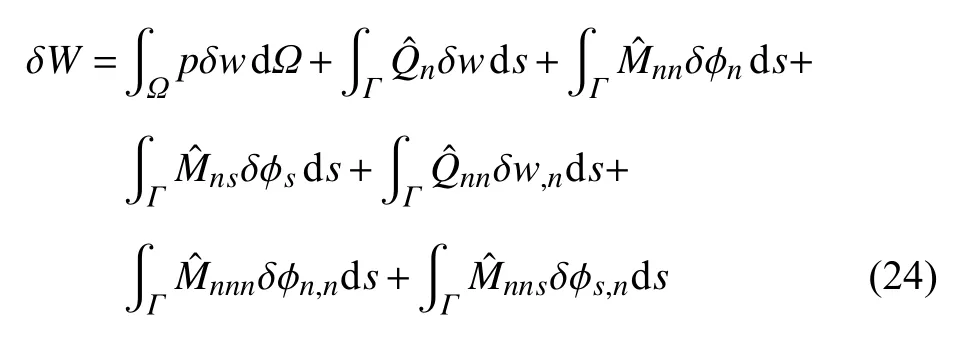
由式(6)和(7)可知,系统动能的一阶变分为
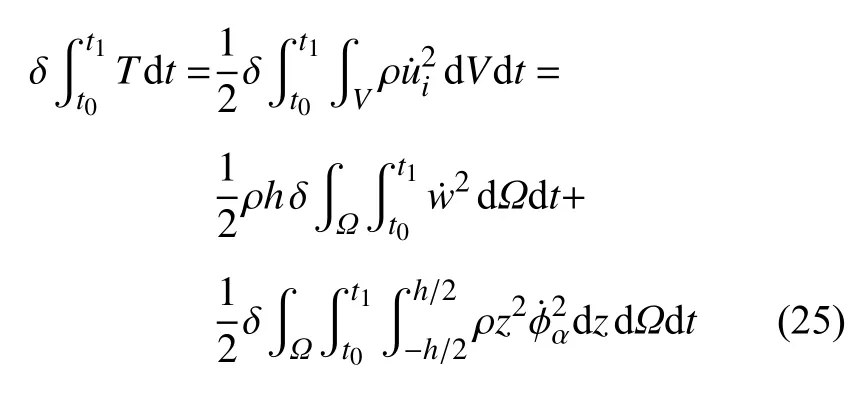
哈密顿原理指出,能量取驻值条件是系统所有可能运动形式的必要条件,即
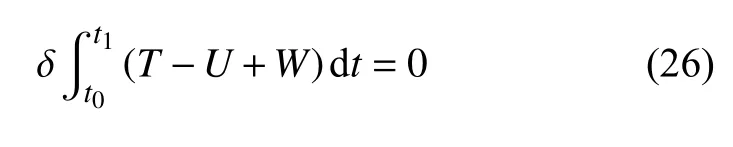
将I1~I4的表达式代入式(13),得到应变能的一阶变分,然后将此变分与式(24) 和式(25) 一并代入式(26),经过一些符号运算,并考虑到 δϕx,δϕy和δw的任意性,整理得Mindlin 板的弯矩和剪力平衡微分方程为1.假定系统在t0 和t1 时刻的位形给定
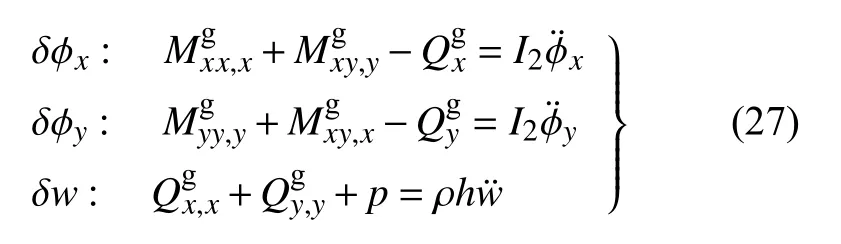
式中,I2=ρh3/12.
边界条件为
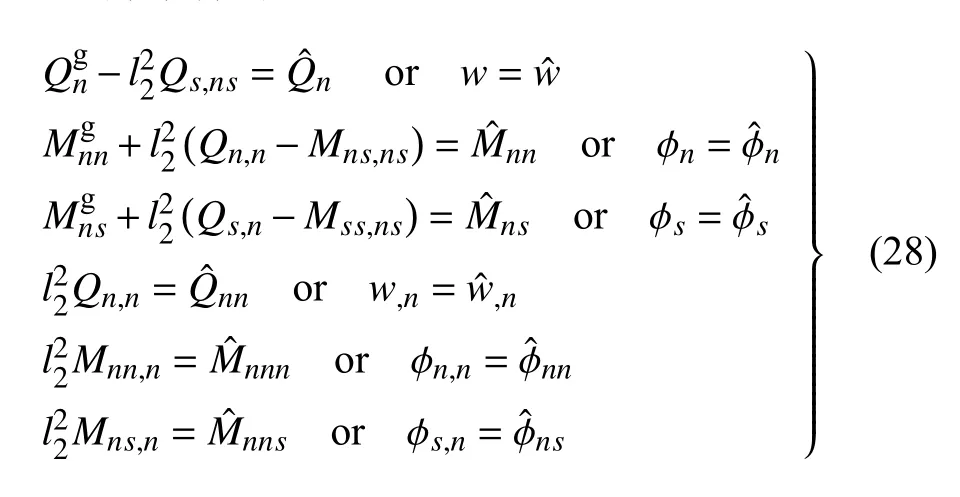
将弯矩和剪力的表达式(11)代入平衡方程(27),得Mindlin 板的控制微分方程为
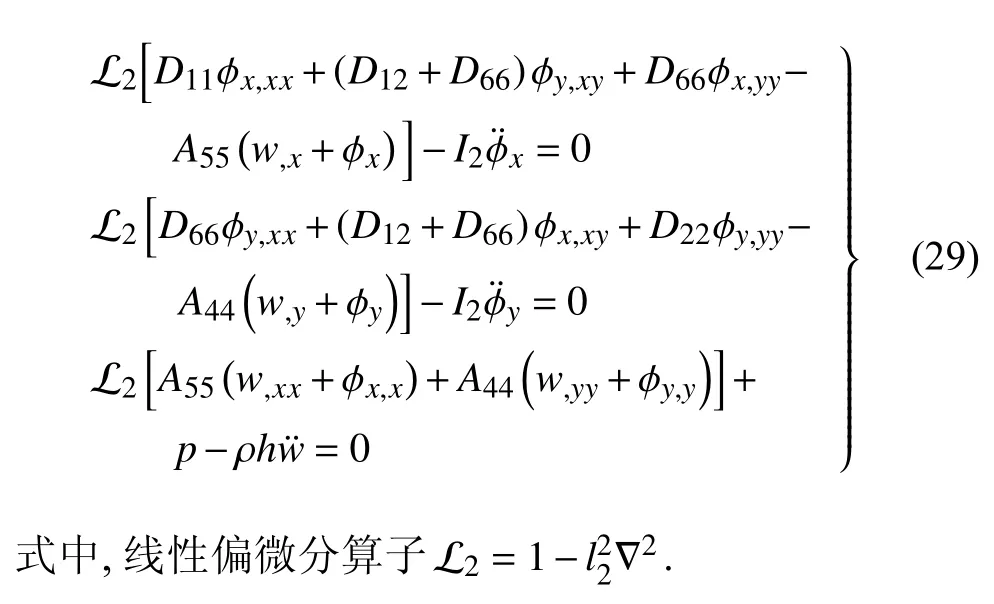
令θ=0,即(n,s)分别替换为(x,y),边界条件(28)改写成直角坐标系框架下的表达式为
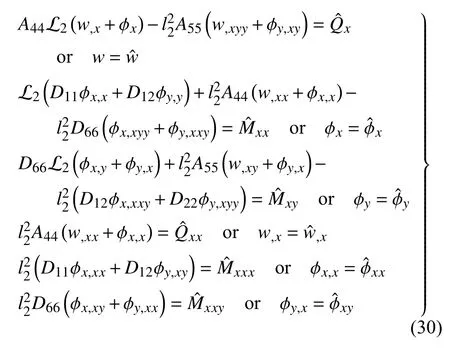
为了同经典Mindlin 板的边界条件相对应,本文仍然称式(28)的前3 式为广义经典边界条件,称其后3 式为非经典高阶边界条件.这是因为,当不考虑应变梯度参数时(即令l2=0),式(28)的前3 式退化为经典边界条件,而其后3 式将变为零,即其后3 式中的边界条件自动满足.
1.2.2 边界条件讨论


表1 矩形Mindlin 板的各种边界条件Table 1 Various boundary conditons of a rectangular Mindlin plate

1.2.3 退化情况讨论
退化情况分成以下两个部分进行讨论.
(1) 退化为Timoshenko 梁的情况
当只考虑板平面一个维度时,即不考虑式(29)2,以上Mindlin 板将退化为对应的Timoshenko 梁的情况,即令式(29)中 ϕy=0,µ=0,ϕx=ϕ,相应的Timoshenko 梁的控制微分方程为
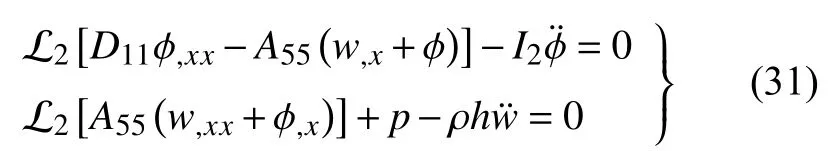
相应的Timoshenko 梁的边界条件为

(2) 退化为相应的Kirchhoff 板的情况
令式(27)中的I2=0,D11=D22=D,ϕα=−w,α,并将该式前两式中的剪力微分后代入其第3 式消去剪力,经整理得其平衡方程为
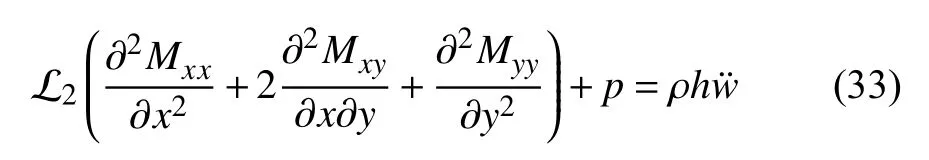
式中,Mαβ为经典弯矩.
除了惯性项外,式(33)与Papargyri-Beskou 等[15]以及Niiranen 等[16]的结果完全相同,这些也间接说明本文Mindlin 板结果的正确性.同时式(33)表明,可以仿照经典板模型平衡方程的体单元推导过程,建立考虑应变梯度板的平衡方程,即只需将经典体单元中的经典弯矩Mαβ和经典剪力Qβ分别用和表示.
1.2.4 角点条件讨论
众所周知,经典Mindlin 板不含任何角点条件,这是因为该模型考虑了转角 ϕα的影响,使得其在应变能变分时,不出现对环向的偏导数引起的[32].
本文的创新工作之一就是首次澄清了在应变梯度理论框架下,Mindlin 板是否存在角点条件的问题.该角点条件仅由式(20)和式(23)给出,其表达式可改写为
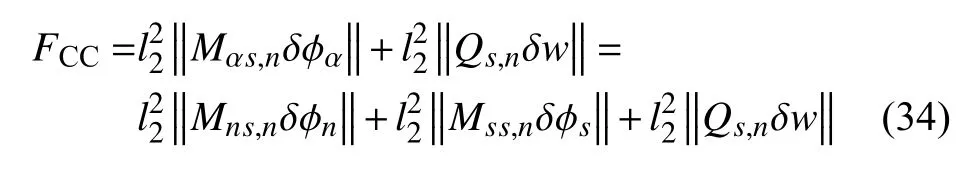
利用张量的坐标不变性,式(34)在直角坐标系框架下为
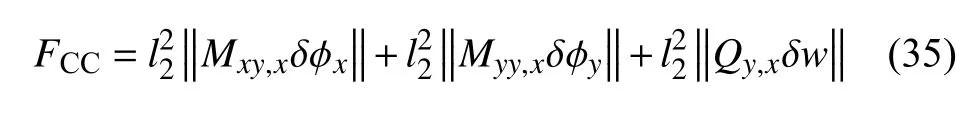
由式(34)或式(35)可知,角点条件由3 个部分组成.第1 部分表明经典扭矩对法向偏导数的影响,第2 部分表明经典环向弯矩对法向偏导数的影响,第3 部分表明经典法向剪力对法向偏导数的影响.
式(35)所示的角点条件可由式(11)进一步改写成以下位移形式
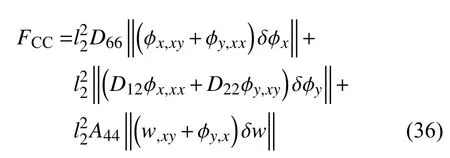
2 结论
针对现有文献对简化的应变梯度Mindlin 板的边值问题及角点条件缺乏系统研究的问题,本文采用变分原理得到了变分自洽的边界条件及角点条件,揭示了双应力如何影响高阶边界条件及角点条件的本质.本文结果首次回答了为什么经典Mindlin板不存在角点条件而本文模型存在角点条件的问题.本文主要创新点如下.
(1)应变梯度Mindlin 板的控制微分方程是一个解耦后12 阶偏微分方程,需要每个矩形边提供6 个边界条件,即3 个广义经典边界条件和3 个高阶边界条件.
(2) 高阶边界条件有多种可能的选取方式,文中讨论并给出了矩形板和圆板可能的边界条件表达式.
(3) 经典Mindlin 板不存在任何角点条件,本文首次发现非经典Mindlin 板存在角点条件: 由经典扭矩、经典弯矩和经典剪力对他们各自物理量的法向偏导数的贡献.
