超静定梁−柱的解析解研究1)

李银山 * 丁 千 李子瑞 * 郭春霞 ** 孙永涛 ,2) 柳占立 ,3)

* (河北工业大学机械工程学院工程力学系,天津 300401)

† (天津大学机械工程学院力学系,天津 300350)

** (西安建筑科技大学理学院力学系,西安 710055)

†† (清华大学航天学院工程力学系,北京 100084)

引言

超静定梁−柱因其刚度大、强度高等优势在土建、水利和机械工程中较为常见[1-5].作用在梁−柱上的轴向压力对梁的弯曲特性有较大的影响,此时,梁−柱的内力、应力及变形并不与轴向压力的大小成正比[6-7],梁−柱的弯曲问题本质上是一个非线性问题[8].计算超静定梁−柱时,既要考虑梁的超静定特性又要考虑轴向力的非线性特性,因而其力学分析就更加复杂,准确快速地计算出超静定梁−柱的内力和变形对其安全设计具有重要意义.

工程设计人员在设计超静定梁−柱时,需要计算其最大变形和最大内力,很多学者围绕这一问题展开研究,并涉及到了方方面面.其中,早期主要偏重于对二阶非齐次常微分控制方程的精确求解,相关教材中的理论研究表明[1,9-11],超静定梁−柱的精确解较为复杂,若采用精确解来分析实际问题,计算过程较为繁琐且计算量大.而后,随着研究的逐步深入,学者们开始聚焦于分析超静定梁−柱的新的方法.陈连[12]采用奇异函数法推导出超静定梁−柱弯曲变形的普遍表达式,利用边界条件确定约束反力并求出了变形,其解答是由奇异函数表示的.Girhammar等[13-14]利用变分法从理论上分析了任意边界条件下梁−柱的求解方法,仅得到简支梁−柱的求解结果,对于其他边界条件复杂繁琐.Aristizabal-Ochoa 等[15-17]研究了具有半刚性连接的超静定Timoshenko 梁−柱的大挠度和后屈曲行为.Liew 等[18]利用连续强度法预测了轴向力和弯曲载荷联合作用下工字形截面和箱形截面的极限截面抗力.

随着计算机的发展,出现了一系列求解工程中超静定梁−柱问题的新方法.蒋纯志[19]利用分布传递函数方法研究了任意边界条件和复杂外力作用下的梁−柱的弯曲问题,与MATLAB 软件相结合,计算得到了解析解.Arboleda-Monsalve 等[20]采用矩阵法研究了轴向力对双参数弹性地基上广义端部条件下梁−柱变形的影响.Untaroiu 等[21-22]开发了股骨的特定对象有限元模型,对交通事故引起的轴向和弯曲载荷共同作用下的股骨的耐受性进行了数值研究.Russell[23]利用有限差分法和矩阵递归关系求解了广义梁−柱的弯曲问题.文献[24-28] 通过试验研究和数值分析,探讨了同时承受轴向力和弯曲载荷的钢柱或混凝土柱的承载力的设计方法.

从现有文献来看,轴向压力对超静定梁−柱变形的影响的精确解结果较为复杂,不便于工程应用.有限单元法只能得到数值解,无法得到解析式.连续分段独立一体化积分法是李银山等[29-32]提出的一种求解力学中有关微分方程问题的有效方法,与计算机软件相结合,具有求解精度高、速度快的特点.本文在连续分段独立一体化积分法的基础上,采用渐进积分法研究超静定梁−柱的弯曲问题,得出了超静定梁−柱在各种载荷作用下的最大弯矩和最大挠度、最大转角关于轴向力放大系数的表达式,所得解答为简单的多项式,便于理解和计算.并将渐进积分法的计算结果与经典的精确解进行比较验证,在迭代仅6 次的情况下即可达到满足工程需要的精度,大大提高了计算速度.且发现对非对称梁−柱,不仅其最大位移和最大剪力的大小随轴向力的增大而增大,而且其最大位移和最大剪力的位置也随轴向力的增大而发生迁移,这一发现填补了现有研究的空白.

1 分布力作用下的铰支−固支梁−柱

1.1 精确解

设长为l、抗弯刚度为EI的梁,仅承受分布载荷q(x).轴向坐标为x,挠度为v.梁的小挠度四阶微分方程为

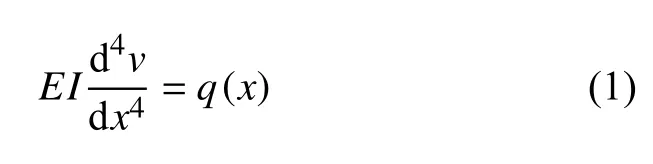
设长为l、抗弯刚度为EI的压杆,仅承受轴向压力F.轴向压力作用下杆的小挠度四阶微分方程为

欧拉临界力公式为

其中,Fcr为临界压力,α为与杆端约束有关的轴向压力临界力系数.

同时承受横向载荷和轴向压力F作用下梁−柱的微分方程为

令

其中,κ为轴向压力比.将式(5)代入式(4)得,梁−柱的无量纲微分方程

现研究同时承受均布横向力(此时q(x)=−q)和轴向力F作用下的铰支−固支梁,如图1 所示.由式(6)可知无量纲微分方程为

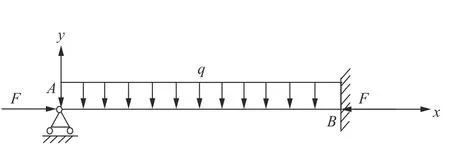
图1 轴向压力与横向分布力共同作用的铰支−固支梁−柱Fig.1 Hinge-fixed beam-column acted by axial force and transverse load

其中

边界条件为

用连续分段独立一体化积分法得到挠度函数

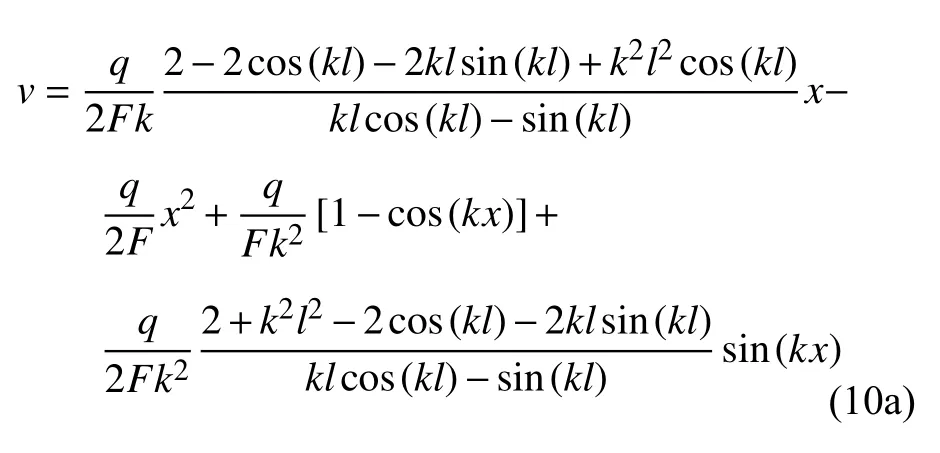
转角函数

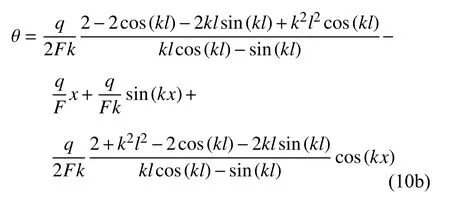
弯矩函数

剪力函数

根据式(10)可以绘制出横向分布力作用下铰支−固支梁−柱的变形图和内力图,如图2 所示.最大转角和最大弯矩的精确解为

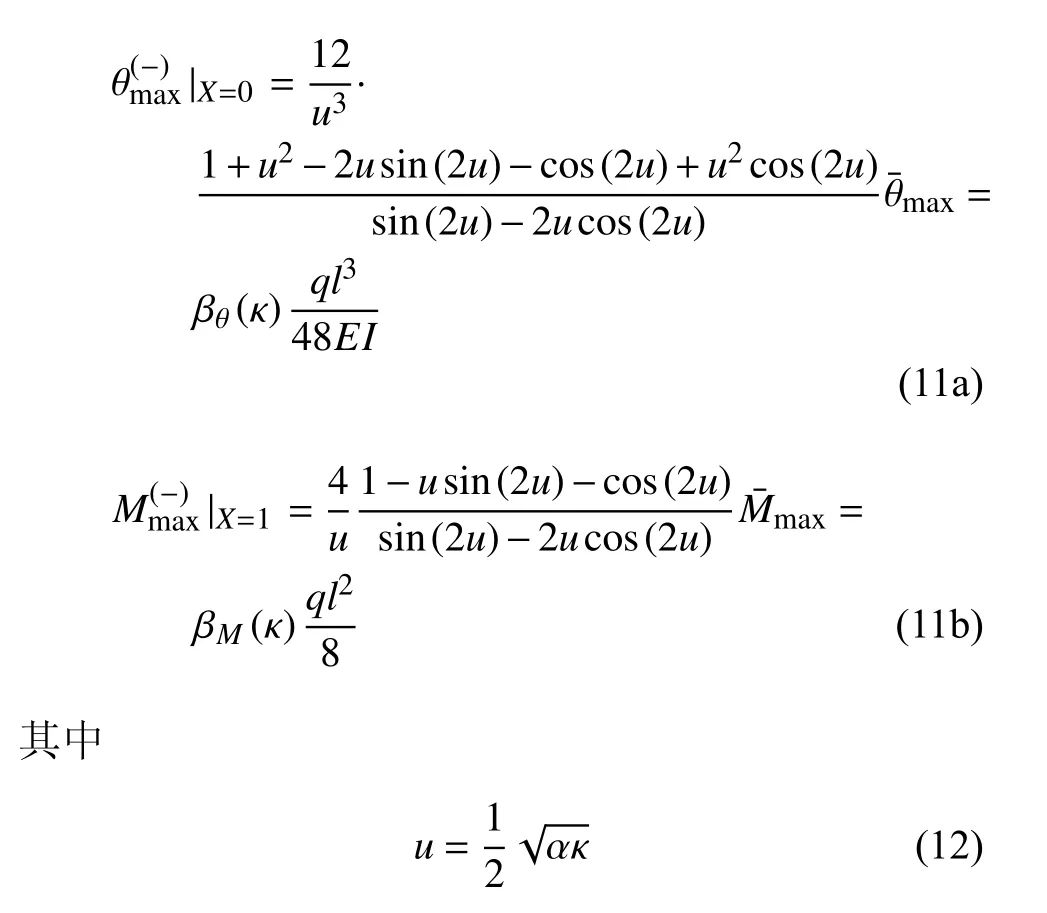
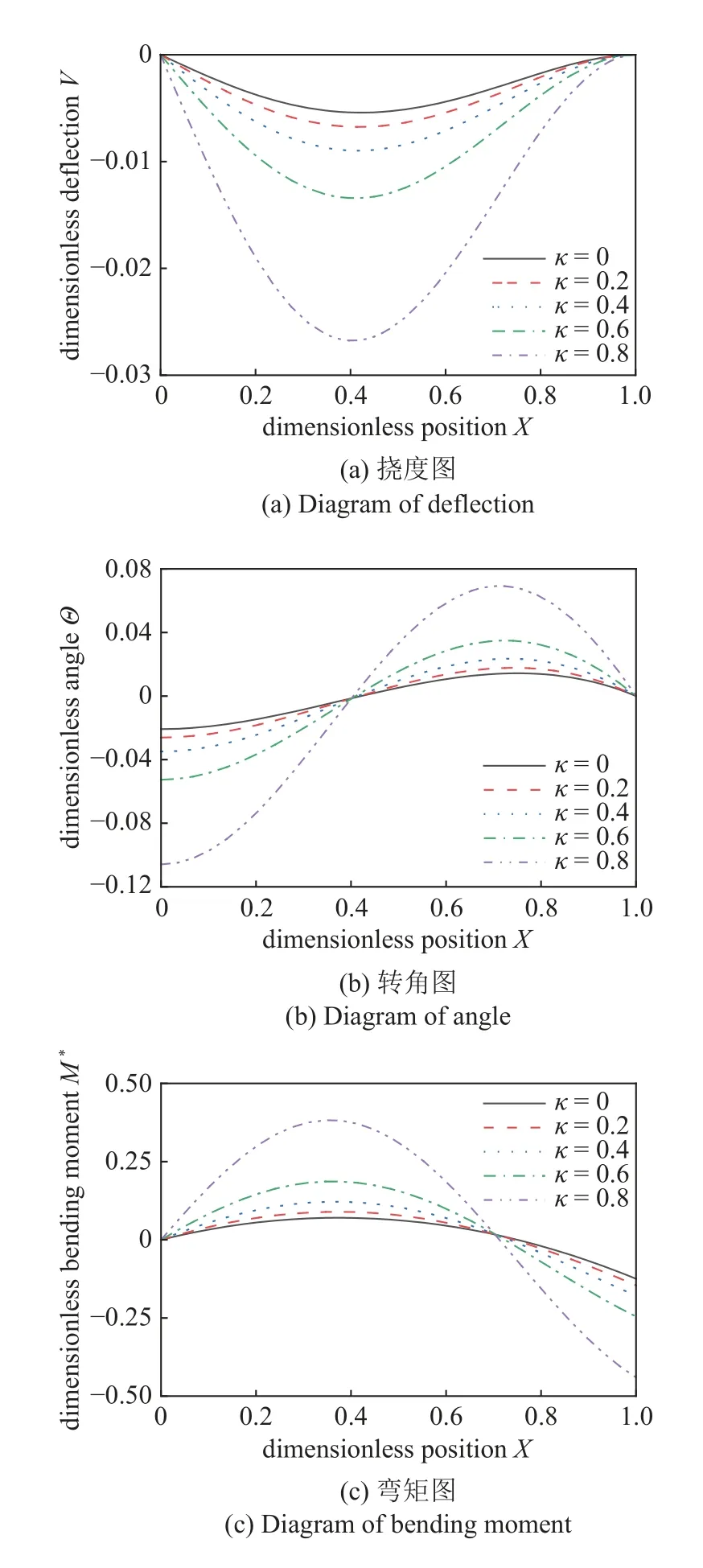
图2 不同轴向力下,横向分布力作用的铰支−固支梁−柱的变形图和内力图Fig.2 Deformation and internal diagram of hinge-fixed beam-column under different axial forces

1.2 最大挠度和最大剪力位置迁移

从图2(a)和图2(d)中的挠度图、剪力图可以看出,随着轴向力的增加,最大挠度、最大剪力的位置发生了迁移,这是新发现的一种现象,称为最大位移和最大内力迁移现象.利用最小二乘回归法可以得到最大挠度和最大剪力的表达式如下.

最大挠度位置

最大挠度和最大剪力位置迁移关系如图3 所示.最大挠度和最大剪力放大系数的位置迁移对照如表1 所示.

图3 最大挠度、最大剪力位置随轴向力系数κ 的迁移Fig.3 Migration of maximum deflection and maximum shear force position with axial force coefficient κ

表1 最大挠度和最大剪力放大系数的位置迁移对照表Table 1 Location transfer comparison table of maximum deflection and maximum shear force amplification factor

1.3 渐进积分法

为了求解微分方程式(7),构造迭代方程如下

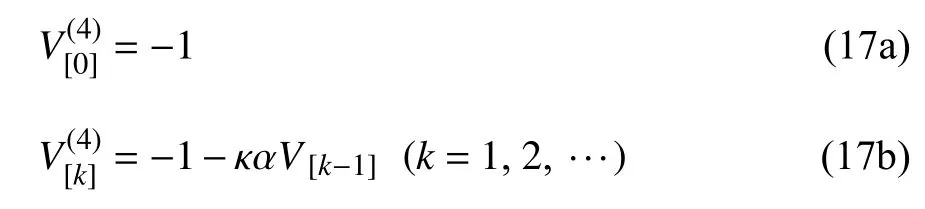
选取无轴向力作用的梁挠度为初始曲线V[0](X).基本方程为

边界条件为

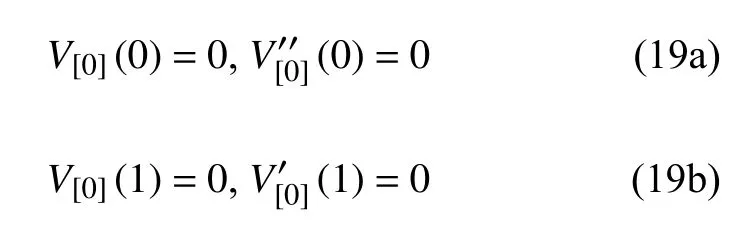
由连续分段独立一体化积分法解得

由式(17b)知,基本方程为

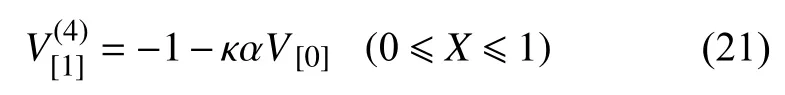
边界条件

由连续分段独立一体化积分法解得

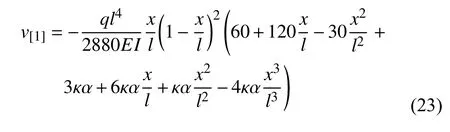
继续迭代就可以得到更精确的挠度表达式.

1.4 弯矩和变形的最大值

由式(23)可求出迭代一次(在x=X0L处) 挠度的最大值为

依次类推,一直迭代到第六次,可得最大挠度、最大转角和最大弯矩的轴向力放大系数

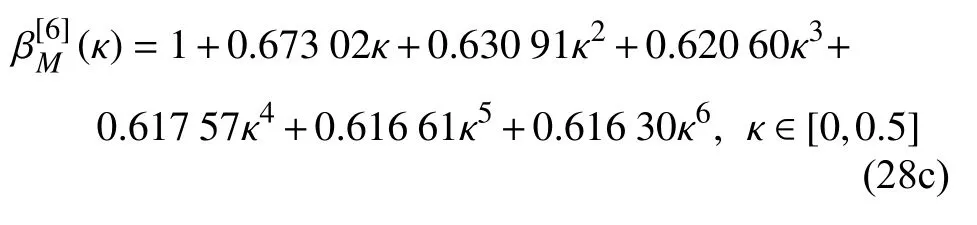
根据本文的方法,轴向压力与横向分布力共同作用时铰支−固支梁的内力和变形均可表示为类似于式(28)的简单多项式.

迭代六次后,每次迭代的最大挠度、最大转角和最大弯矩与精确解的对比如图4 所示.利用渐进积分法求解,迭代六次时最大挠度βv、最大转角放大系数βθ和最大弯矩放大系数βM的计算结果与精确解的对比如表2 所示.

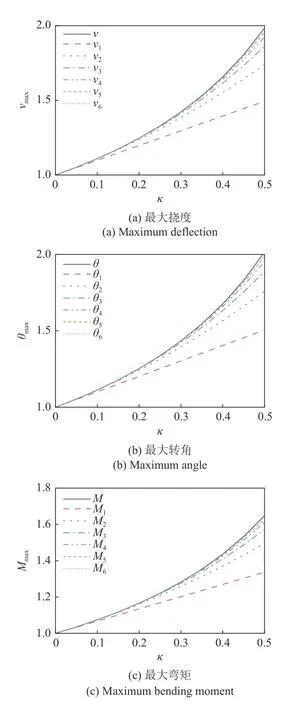
图4 横向分布力作用下铰支−固支梁−柱前六次迭代最大变形和最大弯矩与精确解的对比Fig.4 Comparison between the maximum deflection,maximum angle and maximum bending moment in the first six iterations and the exact solution

从图4 可以看出,横向均布载荷作用下的铰支−固支梁−柱迭代计算出的最大挠度、最大转角和最大弯矩随迭代次数的增加而逐渐趋近于精确解.

从表2 可以看出,当κ∈[0,0.5]时,即当梁−柱所受的轴向力是欧拉临界力的1/2 以内时,误差在1%以内,此时,梁−柱的最大变形和最大弯矩约是没有轴向力时的2 倍.

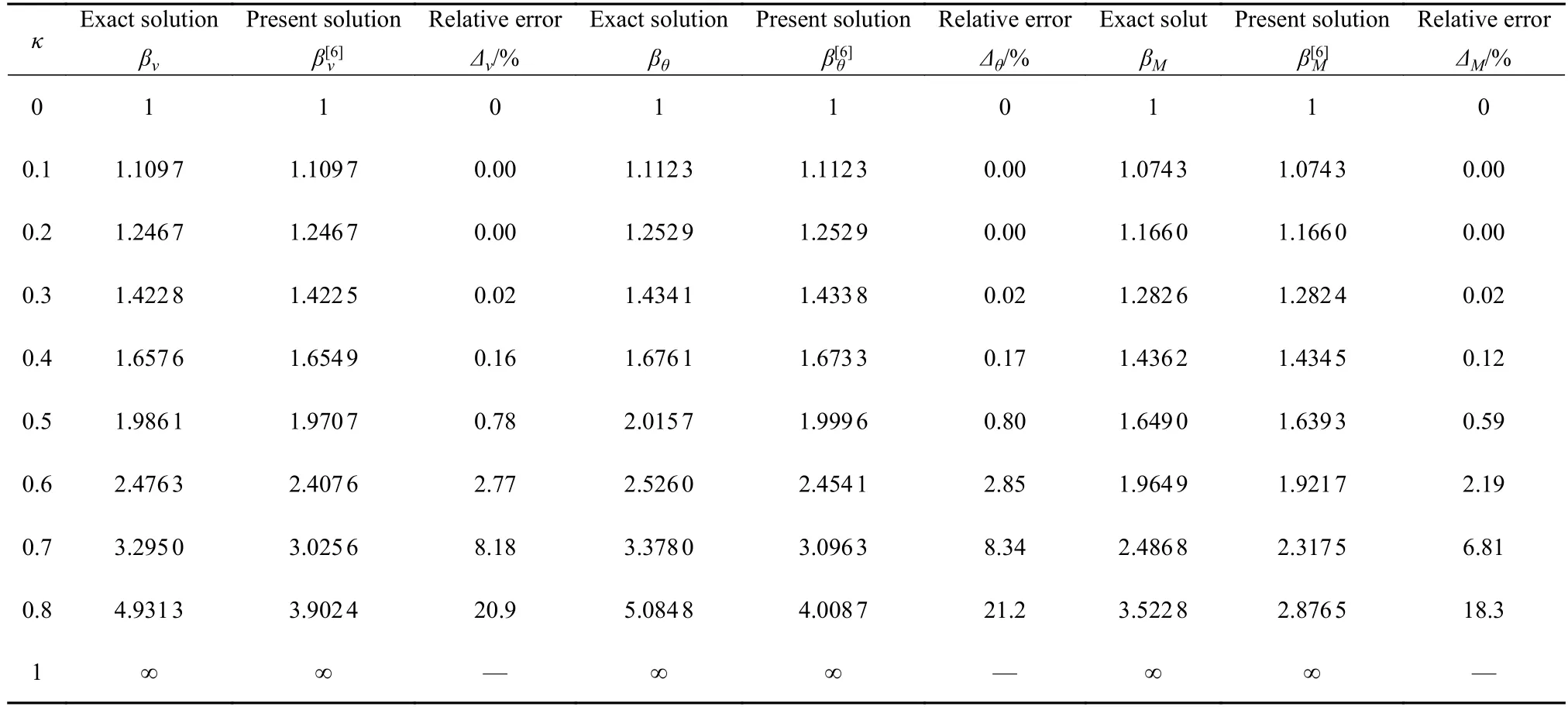
表2 横向分布力作用的铰支−固支梁−柱放大系数对比Table 2 Comparison of hinged-fixed beam-column amplification coefficients under continuous transverse load

2 分布力作用下的固支−固支梁−柱

2.1 精确解

本节研究同时承受连续横向分布力 (此时q(x)=−q)和轴向集中力F作用下固支−固支梁−柱,如图5所示.

图5 轴向力与横向分布力作用的固支−固支梁−柱Fig.5 Fixed-fixed beam-column acted by axial force and transverse load

由式(6)可知无量纲微分方程为

其中

边界条件为

用连续分段独立一体化积分法可得

根据式(32),可以绘制出横向分布力作用下固支−固支梁的变形图和内力图,如图6 所示.

图6 不同轴向力下,横向分布力作用的固支−固支梁的变形图和内力图Fig.6 Deformation and internal diagram of fixed-fixed beam-column under different axial forces

最大挠度,最大弯矩的精确解为

2.2 最大转角和最大剪力位置迁移

从图6(b)和图6(d)中的转角图和剪力图可以看出,随着轴向力的增加,最大转角和最大剪力的位置发生迁移,这是新发现的一种现象,称为最大位移和最大内力迁移现象.利用最小二乘回归法可以得到最大转角和最大剪力表达式如下.

最大转角位置

最大剪力位置迁移图如图7 所示.

图7 最大转角和最大剪力位置随轴向力系数 κ 的迁移Fig.7 Migration of maximum angle and maximum shear force position with axial force coefficient κ

最大转角和最大剪力放大系数的位置迁移对照如表3 所示.

表3 最大转角和最大剪力放大系数的位置迁移对照表Table 3 Comparison of position migration of maximum angle and maximum shear amplification coefficient

2.3 渐进积分法

构造迭代方程如下

选取无轴向力作用的梁挠度为初始曲线V[0](X).基本方程

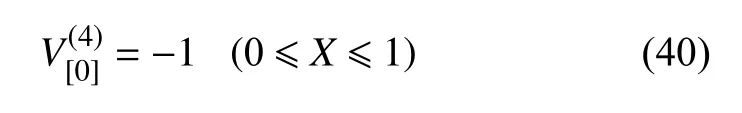
边界条件

由连续分段独立一体化积分法解得

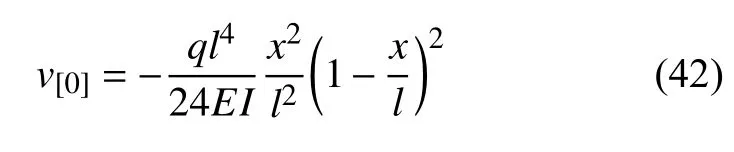
由式(39b)求第一次近似变形曲线,基本方程为

边界条件

由连续分段独立一体化积分法解得

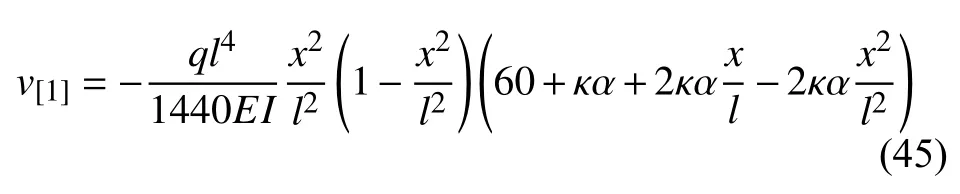
2.4 弯矩和变形的最大值

由式(45)可知,最大挠度出现在跨中截面,为

依次迭代到第六次,得到的最大挠度、最大转角和最大弯矩的放大系数分别为

迭代六次后,每次迭代的最大挠度、最大转角和最大弯矩与精确解的对比情况如图8 所示.利用渐进积分法求解,迭代六次时最大挠度放大系数βv和最大弯矩放大系数βM的计算结果如表4 所示,并与精确解进行了对比.

图8 梁−柱前六次迭代时最大变形和最大弯矩与精确解的对比Fig.8 Comparison between the maximum deflection,maximum angle and maximum bending moment in the first six iterations and the exact solution

表4 分布力作用的固支−固支梁−柱放大系数对比Table 4 Comparison of the fixed-fixed beam-column amplification coefficient under continuous transverse loading

从图5 和表2 可以看出,当κ∈[0,0.5]时,本文的解答与精确解的误差在1%以内.

3 结论

本文从力学模型研究入手,建立了铰支−固支、固支−固支两种边界条件下的超静定梁−柱在轴向力和分布载荷共同作用下弯曲问题求解的通用模型,推导出超静定梁−柱弯曲变形的迭代微分方程和程序化求解内力和变形的通用程序,用Maple 语言开发出相应的求解程序.

采用连续分段独立一体化积分法求解了横向分布力作用下铰支−固支、固支−固支两种边界条件下超静定梁−柱的弯曲问题,得到了挠度函数、转角函数、剪力函数和弯矩函数的精确解析解,绘制了不同轴向力 (κ=0,0.2,0.4,0.6,0.8)时的挠度图、转角图、弯矩图和剪力图.进一步得到了两种边界条件下超静定梁−柱最大位移和最大内力的解析表达式，式(13)、式(15)、式(35)和式(37)给出了最大位移和最大内力的位置迁移解析表达式,图3 和图7 绘制了最大位移和最大内力的位置迁移图.本文新发现了梁−柱最大位移和最大内力的位置随轴力变化的迁移现象.

由于精确解析解是复杂函数,本文为了满足工程设计需要,构造了求解超静定梁−柱的四阶挠度微分迭代方程,利用渐进积分法求解得到了最大挠度、最大转角和最大弯矩等用轴向力放大系数表示的多项式解析函数解.图4 和图8 绘制出了六次迭代的最大挠度、最大转角和最大弯矩与精确解的对比图;表2 和表4 列出了迭代六次时最大挠度、最大转角和最大弯矩放大系数的多项式解与精确解的误差对比表.结果表明在迭代仅6 次的情况下,当超静定梁−柱所受的轴向力约为欧拉临界力的 1/2 以内时,可将误差控制在1% 以内,满足工程精度要求.

由于采用计算机积分求解计算速度快,载荷和刚度不需要简化,求解过程简洁方便、快速准确,本文提出的渐进积分法是一种可靠又快速的方法,具有重要的理论意义和工程实用价值.