上土下岩地层中平面SH 波的传播特性分析

周 俊，石文革，董玉飞，路世伟，杜国锋，刘洪宇

（1. 中国葛洲坝集团第三工程有限公司, 陕西 西安 710077；2. 长江大学城市建设学院, 湖北 荆州 434023）

目前，钻爆法广泛应用于地下工程建设中，在实现经济、便捷、高效施工的同时，其产生的爆破地震效应也是公认的爆破“公害”之首[1-2]。为保证爆破施工邻近建（构）筑物的安全正常运行，研究爆破地震波的传播规律具有重要的工程应用价值。

对于爆破地震波的传播规律，学者们已开展了大量研究工作。胡国忠[3]运用地震波理论对监测资料进行分析，研究了地下工程爆破开挖时地面爆破的振动特性。王玉杰等[4]研究了完整花岗岩体中爆破地震波的传播规律。董永香等[5]通过实验和数值模拟方法，分析了不同组成的多层介质对应力波传播特性的影响。Smerzini 等[6]研究了平面和柱面水平剪切（shear horizontal，SH）波入射地下结构的动力响应特性及其对地面位移的影响。王猛等[7]通过爆炸力学理论和数值计算方法，研究了炸药在土岩介质中爆炸的动力响应规律。王超等[8]基于模拟、实测数据验证和量纲分析方法，研究了不同埋深隧道爆破地震波在邻近地表一定范围内的反射叠加规律和地表振动速度衰减规律。张震等[9]、高文学等[10]、汪平等[11]通过数值模拟与现场监测相结合的方法，研究了浅埋隧道爆破振动的传播规律。陈学军等[12]运用萨道夫斯基修正公式对采集的数据进行研究，探讨了不同情况下爆破振动强度的衰变规律以及振动对岩溶塌陷的影响。Jayasinghe 等[13]根据现场试验，分析了应力波在土壤和岩石中以及土壤与岩石之间的界面上的传播规律。朱斌等[14]进行了下穿预埋燃气管道的现场爆破试验，通过应变及爆破应力波理论分析了爆破过程中爆破地震波的传播特点。高启栋等[15]通过理论和数值模拟，对考虑爆源特征的岩石爆破诱发地震波的波形进行了研究。王秉相等[16]使用PFC3D 软件研究了应力波在散体颗粒中的传播规律和影响因素。王桂林等[17]以重庆市某管廊甲烷爆炸案例为背景，研究了爆炸作用下地面压强与位移的响应特性。

总体来看，现今关于爆破地震波在一般地层传播规律的研究主要集中在现场监测及数值模拟方面，以现今的技术手段测定土层和岩石内部场分布仍然比较困难。考虑到研究平面SH 波在一般地层的传播规律具有重要意义，本研究试图建立地面振动与土层内部振动的关系，选取爆破地震波中的平面SH 波作为研究对象，基于弹性波动理论，建立半空间上层状地层的刚度矩阵及动力平衡方程组，分析土层与基岩的阻抗比、土层厚度、入射波频率和入射波角度对地表速度与土岩地层界面速度的比值的影响，以期为后续类似工程提供参考。

1 SH 波入射作用下上土下岩的动力刚度矩阵建立

1.1 SH 波入射作用下单层土的动力刚度矩阵

如图1 所示，根据弹性波动理论，SH 入射波的位移函数可写为

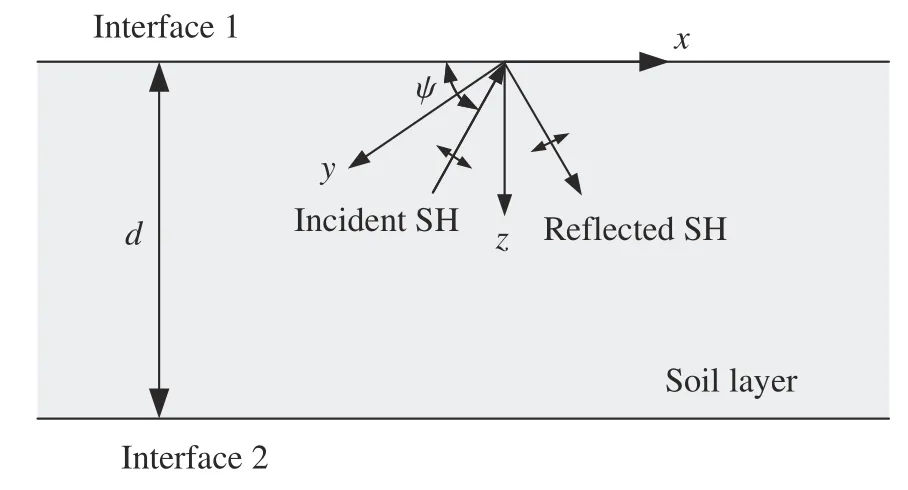
图1 层状地层的局部坐标系Fig. 1 Local coordinate system for a stratified stratum

反射SH 波的位移函数可以表示为

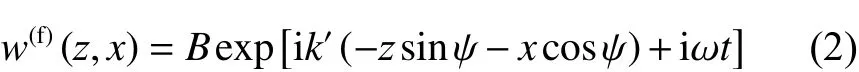
式中：A、B分别为入射波和反射波的幅值；k′为波数，k′=ω/cs，cs为波速，ω 为频率；ψ 为入射波传播方向与x轴的夹角，即入射角；上标“(i)”表示入射，“(f)”表示反射。

1.2 SH 波入射作用下半空间上的层状地层的动力刚度矩阵

地层往往具有上土下岩的特点，并且土层常为多层层状分布，为了进一步推广适用范围，建立了更具一般性的层状地层的动力刚度矩阵。假设n-1 层土层（每层的材料参数为常数）置于基岩上（用N表示）。从土层表面至基岩顶，对各地层界面依次编号，如图2 所示。

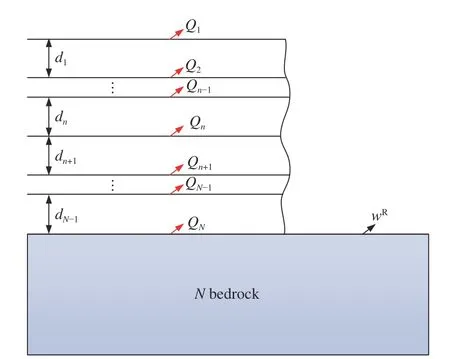
图2 半无限基岩上层状地层示意图Fig. 2 Schematic diagram of stratified strata on semi-infinite bedrocks

根据式(3)，第n层土层的上、下界面位移幅值可表示为

在半无限基岩上表面施加荷载，只会产生去波（辐射条件），在式(4)中令A=0，Q0=-τyz1（下标0 代表半空间自由表面），消去B后得到

对于无阻尼体系，半空间的动力刚度系数为KR=ikζRGR。

图3 总刚度矩阵组装过程Fig. 3 Assembly process of total stiffness matrix

2 上土下岩地层的波传播规律分析

2.1 SH 波入射作用下上土下岩地层的动力刚度矩阵

上土下岩地层简化为无限基岩上覆盖一层厚度为d的土层，如图4 所示。

通过式(15)可得该模型的动力刚度矩阵

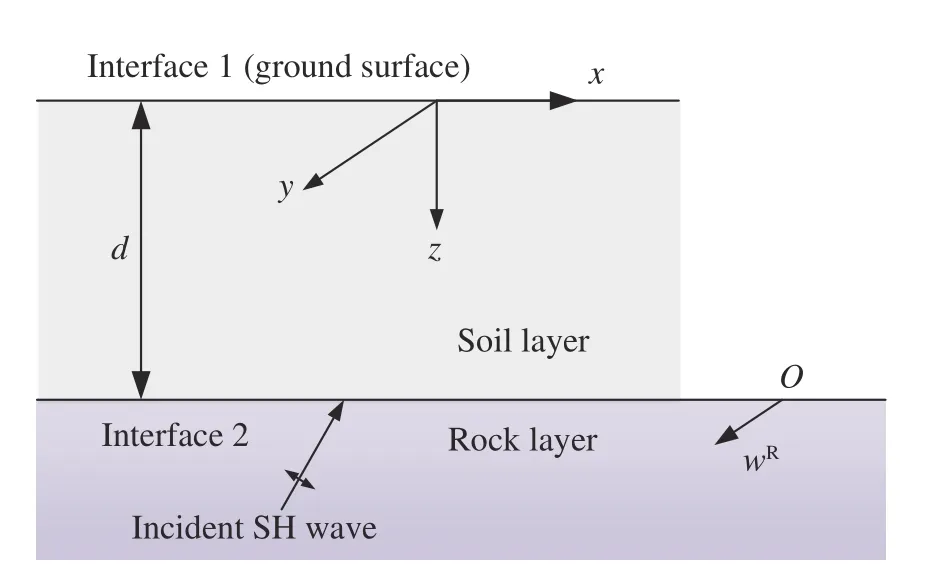
图4 上土下岩地层示意图Fig. 4 Schematic diagram of the upper soil and lower rock stratigraphy

式中：p=ζRGR/(ζG)，Q2=ikζRGRwR， ζR和GR为基岩的物理力学参数。

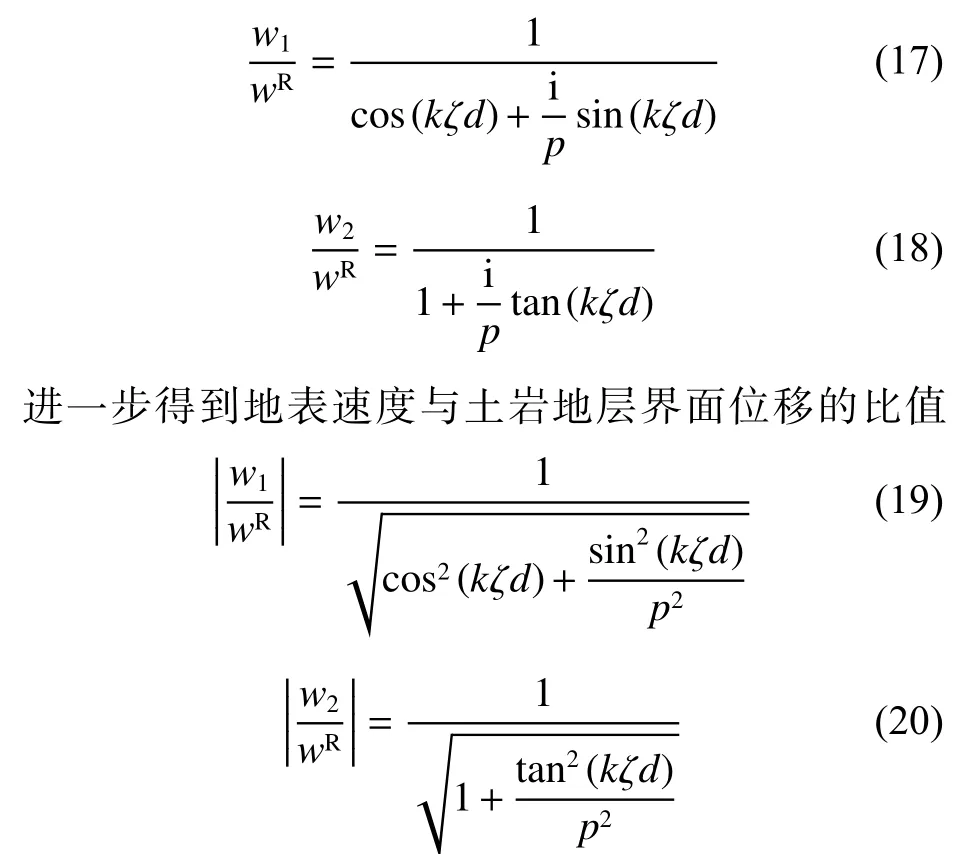
由式(19)和式(20)得到

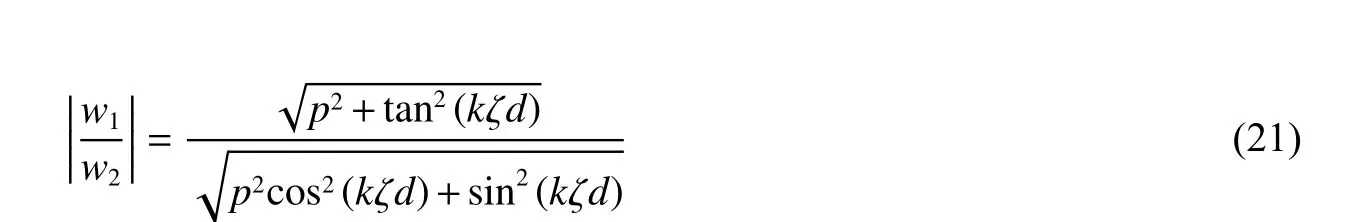
将位移场公式（式(3)）对时间求导，可以得到地表速度与土岩地层界面速度的比值 |u1/u2|=|w1/w2|。

2.2 参数分析

2.2.1 阻抗比和入射角对 | u1/u2| 的影响

波阻抗是抗拒应力波通过的能力，也是应力波扫越一定介质的能力。为了开展更具一般性的讨论，选取入射波频率f为0～200 Hz[19]，定义土层与基岩的阻抗比Z=(ρc)s/(ρc)R，Z分别为0.10、0.50、0.70、0.90 的情况下，入射角ψ 为30°、45°、60°、90°时，绘制 |u1/u2|-f曲线，如图5 所示。

由图5(a)可知：当Z比较小时， |u1/u2|的峰值随着频率的增加缓慢减小，约60 Hz 时峰值由大于1 向小于1 转变，并且SH 波的入射角对峰值几乎没有影响。由图5(a)～图5(d)可知，随着Z的增大，不同入射角下SH 波对应的峰值开始慢慢地向高频分散开来，并且入射角较小的SH 波向高频方向移动的速度大于入射角较大的SH 波。这说明波阻抗较大的土层在高频波作用下的动力响应更加剧烈，并且速度对入射角的敏感性比峰值更强。

图5 不同阻抗条件下入射角对| u1/u2|-f 曲线的影响Fig. 5 Influence of incident angles on the | u1/u2|-f curves under different impedances

2.2.2 不同土层厚度下入射角对 | u1/u2| 的影响

当土层与基层的阻抗比Z=0.19，入射波频率f为0～200 Hz，上覆土层厚度d为2、5、10、20 m，入射角为30°、45°、60°、90°时， |u1/u2|-f曲线如图6 所示。

对比图6(a)～图6(d)可以看出：当覆盖土层厚度不同时， |u1/u2| 的峰值均随着入射波频率f的增大而减小，并逐渐趋于零，入射角对 |u1/u2| 峰 值的影响较小；随着覆盖土层厚度的增加，高频波对应的|u1/u2|峰值逐渐向低频方向移动，随着低频波对 |u1/u2|峰值影响的增强，高频波的影响越来越弱。这说明覆盖的土层越厚，土层的固有频率响应峰值个数越多，且峰值越向低频集中，高频波对 |u1/u2| 的影响程度越弱。

图6 Z=0.19 时不同厚度土层下入射角对 | u1/u2|-f 曲线的影响Fig. 6 Effects of incident angle on the | u1/u2|-f curves under different thicknesses of soil layers when Z=0.19

当土层与基层的阻抗比Z=0.70，入射波频率f为0～200 Hz，上覆土层厚度d为2、5、10、20 m，入射角为30°、45°、60°、90°时， |u1/u2|-f曲线如图7 所示。从图7 可以看出：当土层厚度较小时，土层的固有频率由高频波控制，但是随着土层厚度的增加，高频固有频率对应的峰值逐渐向低频区移动，即低频固有频率对 |u1/u2| 的影响越来越大。从波的入射角来看，当土层厚度较小时，图7(a)中4 个峰值频率为130.6、144.6、163.9、196.3 Hz，不同入射角对应的 |u1/u2| 的最大峰值频率分布范围较大，且主要处于较高的频率；随着土层厚度的增加，如图7(d)所示，4 个峰值频率为12.7、12.7、16.4、19.6 Hz，不同入射角对应的 |u1/u2| 的最大峰值频率分布范围变窄，即入射波角度的影响程度慢慢减弱。这说明：当土层与基岩的阻抗比Z较大且土层厚度较薄时，高频波和入射角对 |u1/u2|的影响较大；随着覆盖土层厚度的增加，不同入射角下的土层固有频率响应峰值向低频移动且相互靠近，即高频波和入射角对 |u1/u2|的影响程度逐渐减弱。

图7 Z=0.70 时不同厚度土层下入射角对 | u1/u2|-f 曲线的影响Fig. 7 Effects of incident angle on the | u1/u2|-f curves under different thicknesses of soil layers when Z=0.70

3 结 论

选取平面SH 爆破地震波，基于波动理论及单层土，建立了一般状况下层状土-基岩地层的刚度矩阵和动力平衡方程组。整体而言，地表速度与土岩地层界面速度的比值 |u1/u2| 的各个峰值随着入射波频率的增加而减小，且第2 个峰值明显小于第1 个峰值，说明实际工程中需要重点关注 |u1/u2|的第1 个峰值对应的频率，即土层的一阶卓越频率。随着土层阻抗的增大，高频部分的响应越来越强烈，受入射角的影响也越来越弱。当土层较薄时， |u1/u2|的高频部分的响应比较明显，但是随着土层厚度的增加，高频部分的响应越来越弱，说明土层的高频滤波作用随着厚度的增加而增强。