扰动作用下爆轰形成机理
2022-12-08张静雯陈先锋孙绪绪
张静雯,彭 澳,陈先锋,孙绪绪
(武汉理工大学安全科学与应急管理学院, 湖北 武汉 430070)
爆轰波是一道强压缩波,跨过爆轰波面的压力和密度均急剧增大,一般气相可燃混合物的爆轰超压是其初始压力的15~20 倍[1],因此在意外爆炸事故中,一旦形成爆轰波,将对周围的基础设施造成毁灭性打击。另外,爆轰作为一种非常重要的超音速燃烧模式,与高性能爆轰发动机密切相关,因此研究人员对燃烧转爆轰和旋转爆轰波开展了大量研究[2-4]。一般有两种爆轰触发途径[5-7]:一种是采用超高点火能量直接起爆形成爆轰波[8-11];另一种是经历较缓慢的火焰加速过程形成爆轰波,即燃烧转爆轰[12-17]。无论是哪种爆轰触发方式,扰动和不稳定性都具有重要作用[14,18],因此在爆轰研究领域,扰动和不稳定性的影响受到了学者们的广泛关注。
Chue 等[19]通过一维数值模拟详细研究了径向密度扰动对爆轰触发的影响,发现扰动频率在爆轰形成过程中具有重要作用。Mazaheri[20]、Ng 等[21]通过一维数值模拟研究得到了相似的结论,并发现密度扰动可放大局部扰动,增强不稳定性。Qi 等[22]详细研究了一维扰动对爆轰触发的影响,发现局部低温点有助于形成爆轰,虽然局部低温点降低了化学反应速率,但是在压力保持恒定的情况下,也可以显著增加局部体积能量密度。Radulescu 等[23]研究了胞格不稳定性对二维弱不稳定爆轰触发的影响,发现胞格不稳定性和多维扰动会抑制非黏性爆轰的形成。Ng 等[18]发现Radulescu 等[23]使用的扰动波长较大,为此开展了不同波长的扰动对爆轰触发影响的研究,发现高频率、低振幅的扰动可以诱导形成小尺寸的不稳定性,有助于爆轰触发。Wang 等[24]通过数值模拟系统地研究了正弦扰动对爆轰触发的影响,发现正弦扰动可以显著降低爆轰触发距离和时间。Xiao 等[25-26]通过数值模拟系统地研究了不同形状障碍物诱导扰动对爆轰起爆的影响,发现了两种不同的爆轰起爆机理:一是较强激波与火焰面相互作用直接起爆形成爆轰,二是较弱激波与火焰面相互作用导致爆轰起爆出现一定延迟。
本研究将通过实验进一步验证扰动在不稳定爆轰触发过程中的重要作用,并结合二维数值模拟详细研究扰动的波长和振幅对爆轰形成机理的影响。虽然前人[18,24]也开展过类似的研究,但是其研究结果在不同类型扰动中是否具有普适性仍不清楚,需要深入研究。本研究结果将有望弥补气相爆轰在该领域的研究空白,证实并完善Ng 等[18]的研究结论。
1 实验系统
1.1 实验装置
图1 为实验装置示意图,基于该装置已经进行了许多相关研究,具体细节见文献[27] ,这里不作详细介绍。本实验中,爆轰管道采用内径为90 mm 的圆管,长度为4 m,其中:前3 m 为触发部分,用来加速形成稳定爆轰波;后1 m 为测试部分,用来记录爆轰触发过程。在管道表面安装若干个PCB 压力传感器(102B06),以记录爆轰波到达时间,由此得到爆轰的平均传播速度。采用烟熏板技术记录爆轰胞格结构,进而统计爆轰胞格尺寸。在触发部分与测试部分之间安装一个阻塞比(φ)为0.923 的孔板,使稳定爆轰波先失效,然后在孔板下游0.5 m 处安装直径为2 mm 的小型圆柱障碍物,用于产生人为的小尺寸扰动,以研究胞格不稳定性在不稳定爆轰触发过程中的作用。图1 给出了3 种不同类型的小型障碍物,其中:D和L分别为障碍物的直径和长度,阻塞比φ 分别为0.03、0.04 和0.07。
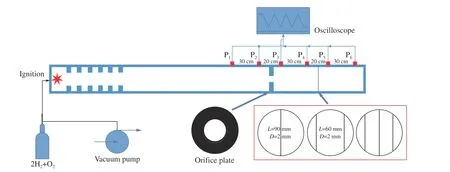
图1 实验装置示意图Fig. 1 Schematic diagram of experimental apparatus
在实验研究中,采用当量比为1 的氢气-氧气混合物作为测试气体。每次实验之前,采用分压法将混合物充入预混罐中,混合至少24 h,以确保混合物的均匀性。混合物的爆轰敏感性可通过不断降低初始压力来实现。爆轰触发临界压力可通过不断降低混合物的初始压力直至爆轰触发不再出现为止来确定。
1.2 实验误差分析
本研究的实验误差主要分为3 个部分。(1) 初始压力的测量误差,包括配气罐中的读数误差和管道中充气初始压力误差。由于所使用的压力表精度为±0.1 kPa(或 0.067%),因此配气罐与管道的初始压力误差均为 0.1 kPa(或 0.067%)。(2) 压力传感器的速度测量误差,由采集软件的采样率控制。测量爆轰前锋到达的时间不确定性为 1 µs,因此相邻两个传感器的时间不确定性为 2 µs。相邻传感器间距有 300 和200 mm 两种,最大爆轰波速度约为2.8 km/s(2H2+O2),因此300 mm 间距内距离误差为5.6 mm(或 1.9%,对于间距为 200 mm 的传感器,则为 2.8%)。同理,速度测量的不确定度同样为53.2 m/s 或1.9%(78.4 m/s 或2.8%)。(3) 爆轰极限确定的误差,主要与爆轰胞格尺寸统计时的人为主观性有关,无法避免。
2 数值模型与方法
为了进一步研究扰动在爆轰触发过程中的作用,通过二维数值模拟详细研究了振幅(A=2.5, 10.0,25.0, 100.0)、波长(η=2, 15, 60, 120)的扰动对爆轰触发机理的影响,这里振幅和波长分别代表高温高压区边界凸起部分的横向尺寸和竖向间距。计算区域(见图2)为一个300×100 的矩形,四周均为反射边界,为了触发爆轰波,在管道左侧设置了一个高温高压区域(p=pShock,T=TShock,其中p为压力,T为温度,pshock和Tshock分别为激波压力和温度)。为了得到稳定传播的爆轰波,当反应波面接近管道末端时,通过程序将管道后2/3 部分剪切并粘贴到管道的前2/3 部分,管道后1/3 部分继续设定为混合物初始状态,通过该方法波面便可在管道内循环往复传播直至稳定。数值模拟的具体细节见文献[28-29]。
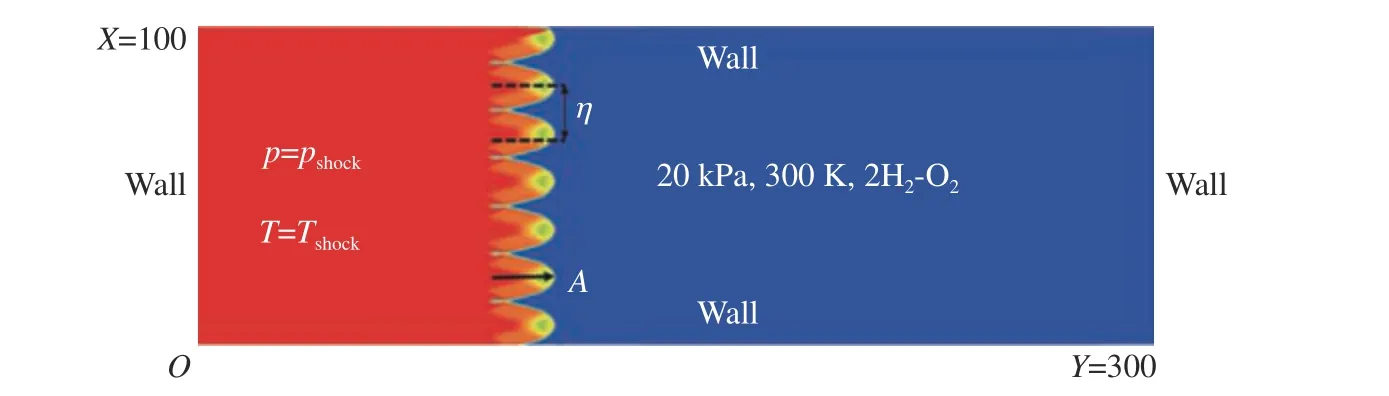
图2 计算区域示意图(在当量比为1 的氢气-氧气混合物中引入振幅为A、波长为η 的扰动)Fig. 2 Schematic of calculation zone (A disturbance with the amplitude of A and wavelength of η is introduced to stoichiometric hydrogen-oxygen mixture.)
在数值模型中,控制方程采用忽略黏性和扩散效应的二维欧拉方程,其表达式为

程序中的各状态参数均通过反应物的初始状态参数进行无量纲化
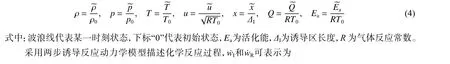

3 实验结果分析
为验证人为引入的小尺寸扰动在不稳定爆轰触发过程中的作用,采用3 种具有较小阻塞比(0.03、0.04 和0.07)的圆柱障碍物产生小扰动。光滑管道内的结果以及利用CHEMKIN 软件包计算得到的理论C-J 速度和燃烧产物中的声速也一并给出用于对比分析。图3 显示了实验得到的平均传播速度与混合物初始压力之间的关系曲线,这里的波面传播速度为管道末端得到的平均传播速度。从图3 可以看出,小尺寸扰动确实能够显著促进爆轰形成,爆轰触发临界压力(pc)从光滑管道内的37 kPa 降低至25 kPa,与Xu 等[30]得到的结论一致,即障碍物可诱导形成更多的横波进而增强波阵面的不稳定性,有助于形成爆轰。这也证实了Lee[31]提出的理论是正确的,即不稳定性或者横波是维持不稳定爆轰传播的重要因素。另外,通过改变混合物的初始压力,仅观察到两种传播模式:(1) 当初始压力大于临界压力时,爆轰以近似理论C-J 速度稳定传播,且本实验得到的传播速度略大于理论C-J 速度,该现象可归因于过驱动爆轰的形成;(2) 当混合物的初始压力低于临界压力时,爆轰完全失效并衰减为爆燃,而当初始压力接近临界压力时,出现突然的速度跳跃,传播速度从理论C-J 速度下降到燃烧产物的声速附近,这里的速度突降可归因于爆轰波的突然失效。
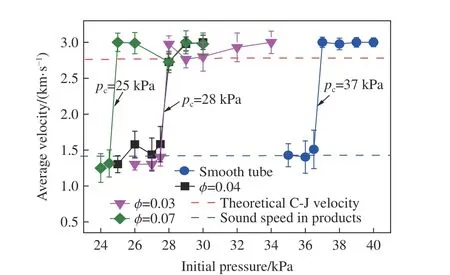
图3 平均传播速度与初始压力之间的关系曲线Fig. 3 Average velocity as a function of initial pressure
为了进一步揭示扰动有助于爆轰触发的内在机理,采用烟熏板技术记录了小型圆柱障碍物之后的爆轰胞格结构。图4 为接近临界压力时不同工况下的爆轰胞格结构记录结果,其中:烟熏板左侧对应小扰动的位置,爆轰从左向右传播。从烟熏板记录中可以发现,激波传播经过小型圆柱障碍物之后,在烟熏板上留下了细小的胞格结构,在细小胞格结构之前是无胞格区域,表明爆轰首先完全失效,然后在小扰动的作用下又重新触发。这些细小的胞格结构正是由重新起爆形成的过驱动爆轰留下的。这里的爆轰形成机理可解释如下:(1) 稳定爆轰波传播通过大阻塞孔板后完全失效,前导激波与火焰面完全解耦;(2) 爆轰失效后传播通过小型圆柱障碍物时,人为引入的小尺寸扰动增强了波阵面的不稳定性,诱导形成较高温度的局部爆炸点,形成了局部爆轰波,并迅速传播覆盖整个反应面,类似于Ciccarelli 等[32]提出的激波-壁面相互作用机理。具体演化过程:爆轰波经过孔板解耦后,变成马赫数约为2.6 的激波,激波面在接触圆柱杆之前演化成弓形激波,导致激波后的压力和温度急剧升高,最终导致爆轰波被直接触发。

图4 临界条件下典型爆轰胞格结构记录Fig. 4 Typical detonation cellular patterns at the critical condition
为了量化临界条件下的爆轰触发机理,人们经常采用D/λ 来量化爆轰触发或失效条件[33-36],其中:D为管道直径或孔板孔径,λ 为爆轰胞格尺寸,本研究所使用的胞格尺寸源自此前的研究[27]。对于本研究所使用的小型圆柱障碍物(直径为2 mm,长度有90 和60 mm 两种),为了与光滑圆柱管道内的实验结果进行对比分析,采用水力直径(DH)表示其特征尺寸。为了便于计算,对障碍物的横截面进行近似,如图5 所示。不同类型的小型圆柱障碍物的水力直径可表示为
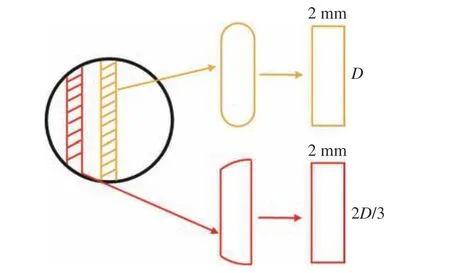
图5 圆柱横截面示意图Fig. 5 Schematic diagram of the cross-section of the cylindrical obstacle
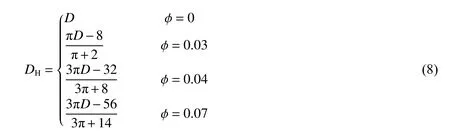
爆轰触发实验结果列于表1。从表1 中可以看出,临界条件下,爆轰触发机理可近似量化为DH/λ>1,与前人提出的爆轰极限标准[37-39]一致,即临界条件下只有当水力直径至少可以容纳1 个爆轰胞格尺寸时爆轰才能形成。DH/λ>1 标准是被普遍接受的用来量化爆轰传播极限的临界判据[37-39]。本研究得到的DH/λ 远大于1,爆轰触发,符合前人提出的标准。然而,这里DH/λ 较大,表明在相同直径下,爆轰传播所需的胞格数较多,即与前人的结果相比,爆轰稳定传播更加困难,该现象可归因于障碍物的阻塞比较小,导致诱导的扰动较弱,不至于快速引起爆轰。

表1 爆轰触发实验结果Table 1 Experimental result of detonation initiation
4 数值模拟结果分析
在分析数值模拟结果之前,首先进行网格独立性分析。图6 为A=2.5、η=2 时不同计算精度下的密度场和胞格结构,这里的计算精度是指1 个ZND 诱导区长度内的网格数量。从图6 可以看出,采用两种计算精度都可以很好地记录爆轰波的波特征,从而清晰地观察横波的分布以及爆轰胞格结构。考虑到本研究的数值模拟主要关注扰动诱导的横波或不稳定性对爆轰起爆的影响,为此以高计算精度(网格数N=20)为例进行分析。
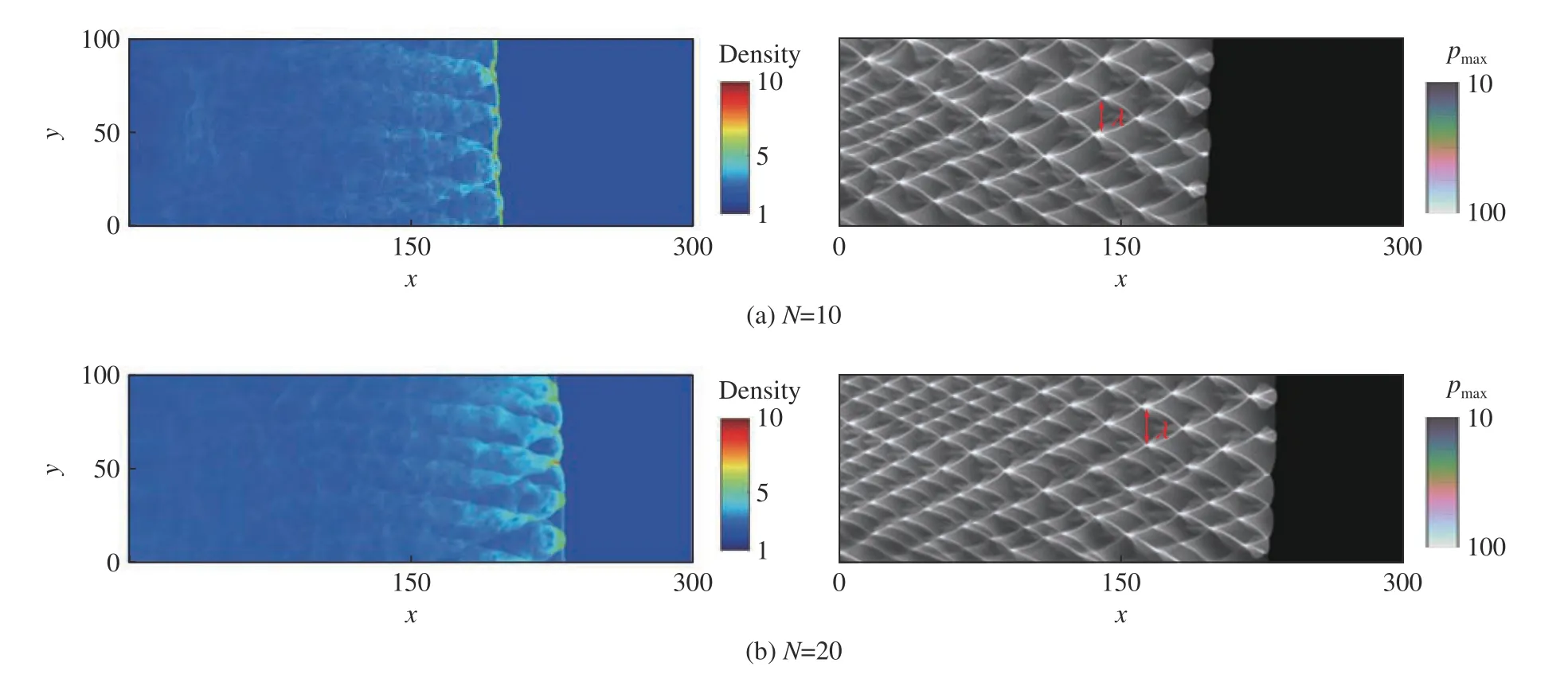
图6 A=2.5、η=2 时不同计算精度下的密度场和胞格结构Fig. 6 Density field and cellular structure for A=2.5, η=2 in the cases of different resolutions
在二维数值计算中,首先固定扰动振幅A=2.5,研究扰动波长η 对爆轰触发的影响,图7(a)显示了爆轰触发所需时间与波长η 之间的关系曲线。可以发现,随着扰动波长的逐渐增大,爆轰触发时间急剧增加,表明扰动波长越小、频率越高,越有利于爆轰触发。然后固定扰动波长η=15,研究扰动振幅A对爆轰触发的影响,如图7(b)所示。可以看出,随着扰动振幅的逐渐增大,爆轰触发时间急剧增加,表明扰动振幅越小,越有利于爆轰起爆。该数值模拟结果类似于Ng 等[18]得到的结论,即低振幅、高频率的扰动有助于形成爆轰。
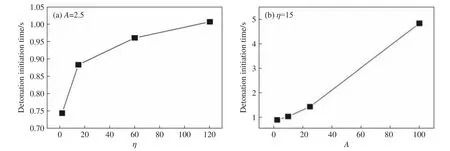
图7 不同工况下爆轰触发所需时间Fig. 7 Detonation initiation time in the cases of different wavelengths and amplitudes
为了进一步解释扰动振幅和扰动波长在爆轰触发过程中的作用,数值模拟得到了不同扰动波长和扰动振幅下的纹影图片,如图8 和图9 所示,这里横纵坐标代表计算区域尺寸,均通过诱导区长度进行了无量纲化处理。以下以图8 为例进行说明。观察图8 可以发现,与高波长情况相比,低波长扰动可以在反应面上诱导产生更多的横波,如A=2.5、η=15 工况中t=0.930 s 和t=1.008 s 时的图像所示,横波可增强波阵面上的不稳定性,更容易诱导形成局部爆炸点。正如Lee[31]所认为的那样,横向不稳定性是维持不稳定爆轰传播的重要原因。如图8(b)所示,在A=2.5、η=15 工况中,t=0.884 s 时局部爆炸点在管壁附近产生,并迅速传播覆盖整个波阵面,诱导形成爆轰。与图8 中的结果类似,从图9 可以发现,扰动振幅越小,越有利于诱导产生更多的横波,在较强横向不稳定性的作用下率先在反应面附近产生局部起爆点,最终诱导产生爆轰波。
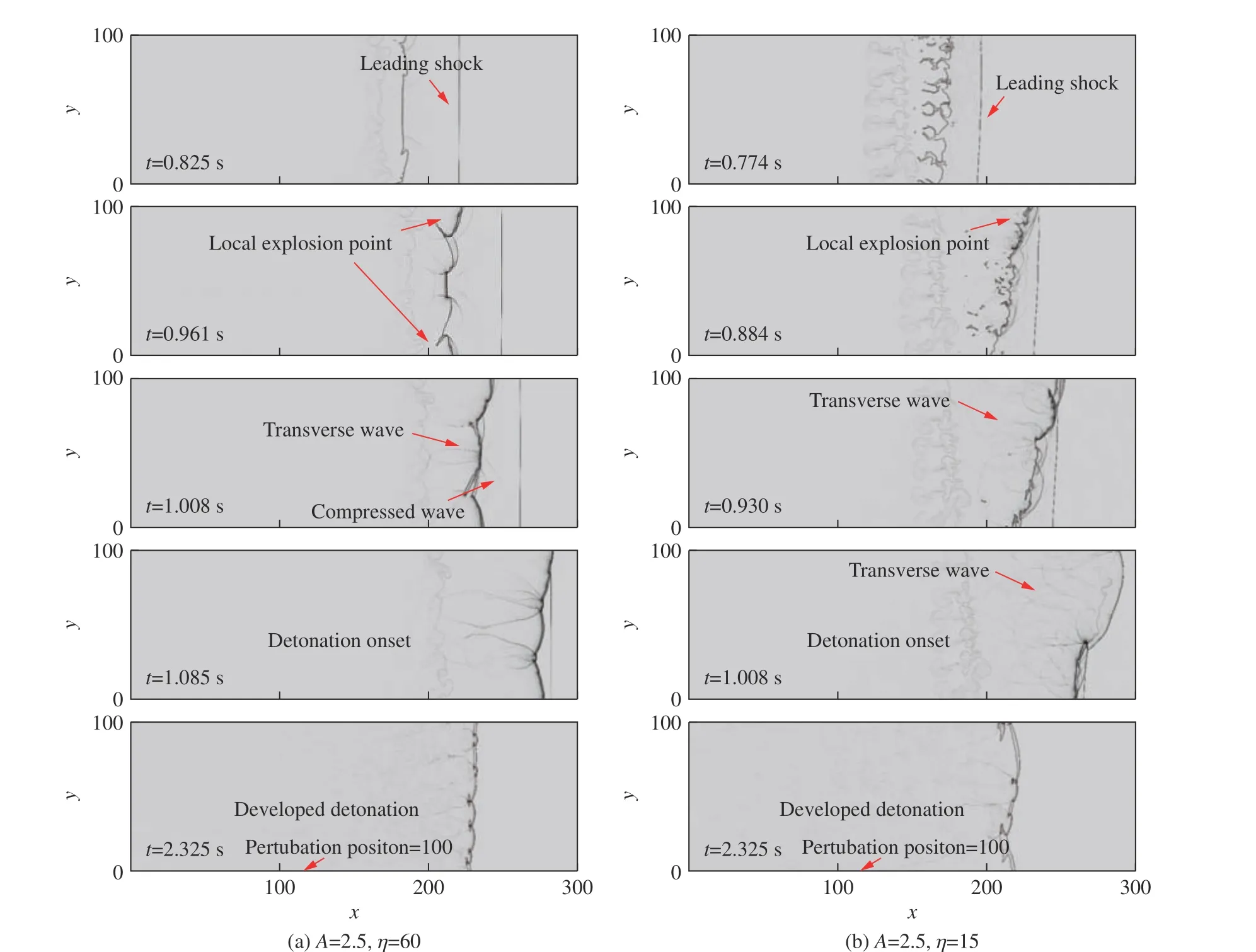
图8 A=2.5 工况下数值模拟得到的纹影结果Fig. 8 Schlieren results in the simulation for the cases of A=2.5
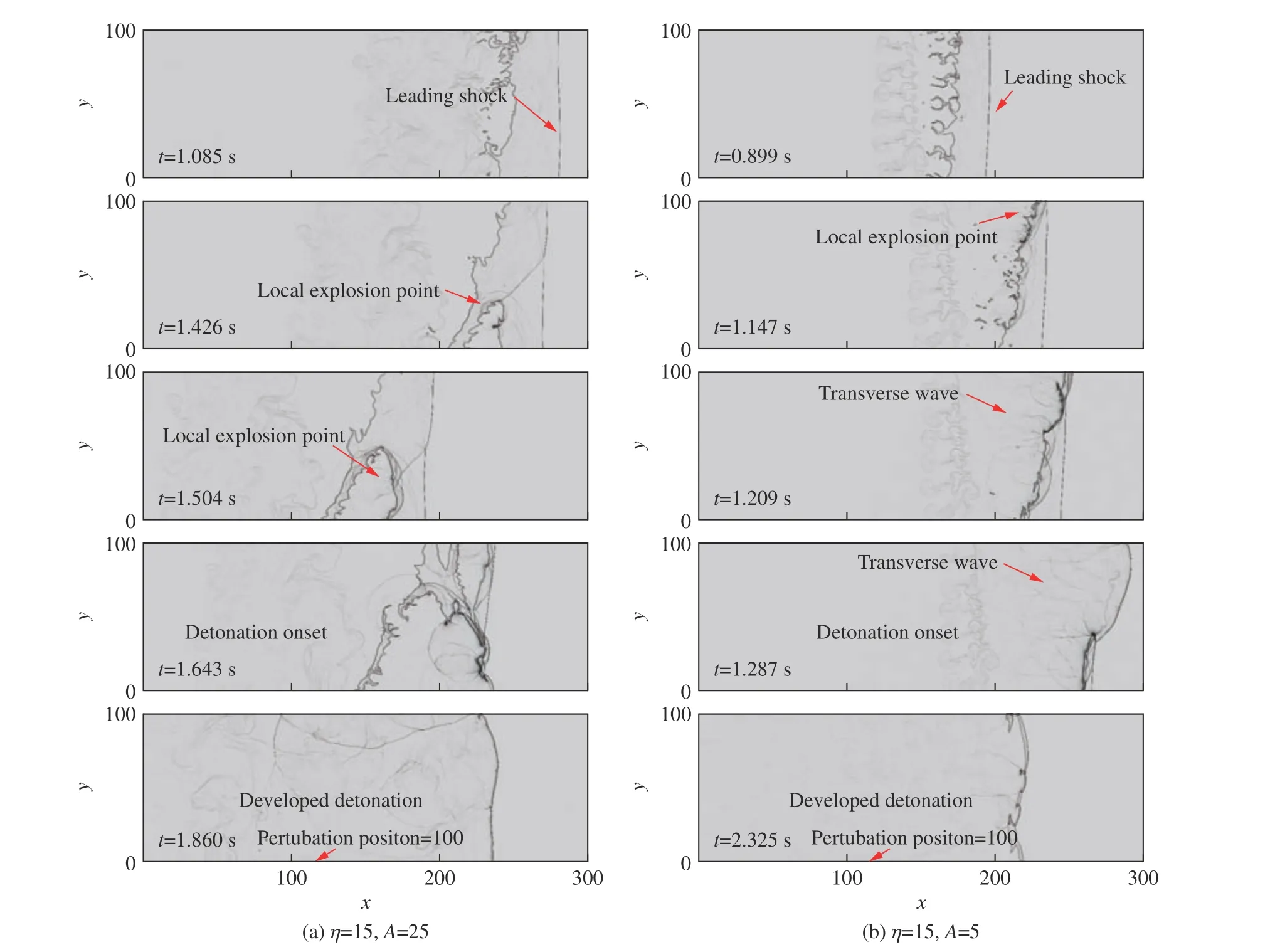
图9 η=15 工况下数值模拟得到的纹影结果Fig. 9 Schlieren results in the simulation for the cases of η=15
5 结 论
通过实验和数值模拟详细研究了扰动在爆轰触发过程中的重要作用。实验结果表明,小扰动可显著促进爆轰起爆,爆轰触发临界压力从光滑管道内的37 kPa 降低到25 kPa。爆轰胞格结构记录显示,小扰动增强了波阵面的不稳定性,诱导形成局部爆炸点,这是导致爆轰触发的重要原因,且极限条件下爆轰触发机理可近似量化为DH/λ>1。数值模拟结果表明,低振幅、高频率的扰动可诱导产生更多的横波,从而增强波阵面的不稳定性,有助于爆轰触发。
感谢H. D. Ng 教授和Xiaocheng Mi 博士在数值计算方面给予的指导与帮助!
