分数阶热弹性理论下中空黏弹性圆柱热弹耦合动力响应
2022-12-01熊春宝虞跨海
郭 颖,熊春宝,虞跨海,梁 斌
(1.河南科技大学 土木工程学院,河南 洛阳 471023;2.天津大学 建筑工程学院,天津 300072)
地下隧洞在轨道交通、石油及天然气开采、地热资源开发、热能储存、核废料处置等能源运输以及军事等工程领域应用广泛,特别是当两个隧洞很近时,相互作用对间距具有敏感性,其耦合动力响应问题直接影响其变形和位移,甚至可能造成失稳。Biot[1]首次提出了耦合的热弹性理论,该理论依旧认为热在介质中的传输速度是无限大的,这与事实不符。为了消除这一现象学者们纷纷提出了可解释热的波动效应的热弹性理论以及相应的数学模型,常用的有:Lord-Shulman (L-S)[2]广义热弹性理论、Green-Lindsay (G-L)[3]广义热弹性理论以及Green-Naghdi (G-N)[4-6]广义热弹性理论。但上述理论不能很好的解释有些黏弹性和反常扩散问题。
Abel首次将分数阶微积分引入到求解等时曲线问题的积分方程当中,并得到了很好的结果。直到1982年,Mandelbrot[7]发现并指出了自然界和工程领域中存在着大量的分数维的事实,并提出该分数维与原有的整数维之间存在自相似的现象,更好地描述了热的波动效应中不好解释的问题。常用的分数阶广义热弹性理论有:Sherief等[8]型分数阶广义热传导理论,Youssef[9]型分数阶广义热传导理论,Ezzat等[10]型分数阶双相滞后广义热传导理论,Ezzat等[11]型分数阶三相滞后广义热传导理论。闻敏杰等[12-13]基于分数阶热弹性理论,研究了热/力源作用下无限大土体中圆形隧洞的热弹性耦合瞬态动力响应以及隧洞内衬砌与土体的相互作用。分数阶微积分的引入对于黏弹性介质的动力特性有了更明确的解释。
弹性介质和黏弹性介质往往被认为均是可以满足连续介质的基本假设的。现有的广义和分数阶广义热弹性理论学者做了大量研究[14-17],发现其研究结果并不能很好的描述介质的松弛和蠕变等黏弹性特性。采用状态空间法,Ezzat等[18]推导了二维黏弹性材料的热黏弹基本方程,并借助Laplace-Fourier双重反变换的方法对问题进行了求解,在已有方程的基础上Ezzat等[19]又结合Kirchhoff理论研究了热导率变换对无限长粘弹性中空圆柱的影响。Kar等[20]在广义热粘弹理论下,研究了均质各向同性黏弹性球壳边界受到温度荷载作用的动力响应问题,对比和分析了两种不同理论中考虑黏弹性与不考虑黏弹性时各物理量之间的差异。Othman等[21]采用Laplace正、反变换法描述了双温度理论下边界受到非高斯激光脉冲的作用的均质各向同性Kelvin-Voigt黏弹半无限大固体的动力响应问题。这些研究大多只对介质的外表面或某个接触面进行了约束,未能考虑两侧均被约束时的动力响应问题。
虽然分数阶广义热弹性理论已取得了较大发展,但将该理论应用于研究外表面作用有热冲击的中空黏弹性柱体热弹性分析的内容鲜有报道。本文基于Ezzat型分数阶双相滞后广义热弹性理论,引入Kelvin-Voigt黏弹性模型从而建立了黏弹性中空圆柱热弹耦合动力模型,考虑轴对称各向同性均质黏弹性中空柱外表面作用有热冲击的情况,利用Laplace变换以及特征值法,给出各物理量解的形式,并通过Laplace数值方便换得到各物理量的数值解。分析了黏弹性中空圆柱热弹耦合问题。分析了荷载作用时间、分数阶系数和黏弹性松弛时间因子对中空圆柱中无量纲位移、温度、径向应力和环向应力的影响。
1 热黏弹模型建立及问题描述
本文基于Ezzat型分数阶双相滞后广义热弹性理论,引入Kelvin-Voigt黏弹性模型建立了均质、各向同性黏弹性中空圆柱热弹耦合动力模型。t=0时刻在圆柱外表面施加热冲击,其外边界自由,内边界绝热且固定(如图1所示)。其不计体力和内热源的基本控制方程
(1)
(2)
(3)
(4)

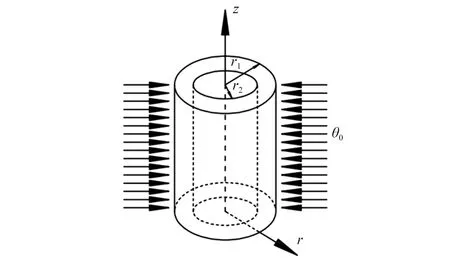
图1 黏弹性中空圆柱热弹耦合问题模型示意图Fig.1 Schematic diagram of the coupled thermoelastic problem of viscoelastic hollow cylindrical
Riemann-Liouville分数阶导数定义如下
(5)
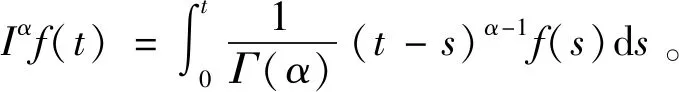
根据研究对象的几何结构对称性,位移分量具有以下形式
ur=u(r,t),uφ=0,uz=0
(6)
基于式(6),应变分量为
(7)
结合柱坐标,体积膨胀率e为
(8)
由式(1)~式(5)可得
(9)
(10)
(11)
(12)
(13)
引入如下无量纲量[22]
(14)
式(9)~式(13)采用式(14)无量纲化处理后仍使用略去各物理量右上方撇号的形式表示,则可进一步写为
(15)
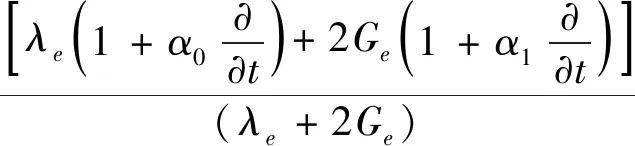
(16)
(17)
(18)
(19)
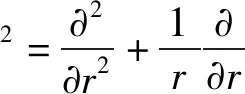
2 问题求解
2.1 拉普拉斯域方程求解
将Riemann-Liouville拉普拉斯变换式[23]
(20)
将式(20)应用于式(15)~式(19)
(21)
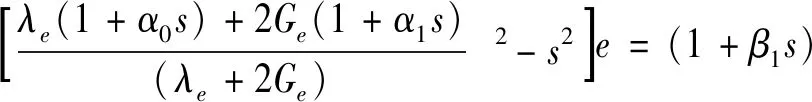
(22)
(23)
(24)
(25)

(26)

(27)
(28)
(29)
(30)
消去式(26)和式(27)中的σ,得到满足e的微分方程
(31)
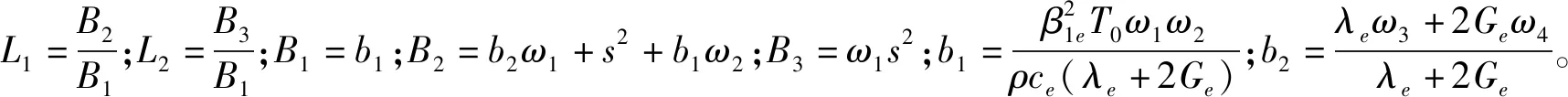
同理,满足θ的微分方程
(32)
式(31)和式(32)可被分解成如下形式
(33)
式(33)的根可展开成
(34)
(35)
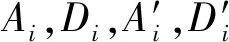
(36)
(37)
(38)
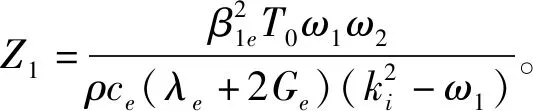
根据式(8)和式(24),有
(39)
根据应变分量式(7)和式(39),可得
(40)
将式(34)、式(38)~式(40)代入式(28)~式(30)中,则有径向应力、环向应力和轴向应力的表达式
(41)
(42)
(43)
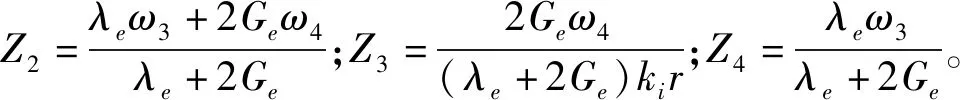
为了确定待定系数A1和Di,须引入问题的初始条件和边界条件,初始条件和边界条件如下:
初始条件

(44)
经过拉普拉斯变换后的边界条件
(45)
(46)
根据初边值条件,结合式(38)、式(39)和式(41),有如下的方程组
(47)
(48)
(49)
(50)
求解Ai和Di的过程较为繁杂,此处不再赘述。
2.2 拉普拉斯数值反变换
为得到时间域中温度、位移、径向应力和环向应力的解答及分布规律,需对拉氏域中得到的各物理量的解进行拉普拉斯反变换。由于拉氏域中各物理量解的复杂性,要对其进行解析反变换几乎是不可能的,只能采取数值反变换的方法。为此,引入如下拉普拉斯数值反变换方法[24]
(51)

在进行拉氏数值反变换时,应用了下面关于贝塞尔函数的渐近展开式
(52)
式中,μ1=4v2。
3 数值结果及讨论
本文以黏弹性中空圆柱为例,在圆柱外表面施加热冲击。结合边界条件最终得到了作用时间、分数阶系数和黏弹性松弛时间因子变化等对该柱体中无量纲位移、温度、将向应力和环向应力的影响。本算例中所需参数同参考文献[25]
其他参数如下:
θ0=1,r1=3,r2=1
当α=1,α0=0,α1=0时,分数阶黏弹性问题将退化为对应的广义热弹性理论。此时,式(37)和式(38)与文献[26]研究圆柱体热弹性问题所求得的解形式相同,这验证了本文根据特征值法在Laplace变换域内所求得结果的正确性。

表1 考虑热弹耦合效应的黏弹性中空计算参数Tab 1 Calculation parameters of saturated porous viscoelastic foundation considering the coupled thermoelastic effect
此外,本文还将MATLAB程序中取α=1,α0=0,α1=0即可退化为整数阶广义热弹性问题,并结合朱海陶等研究中的边界条件对问题进行求解,并将无量纲位移和温度与朱海陶等研究的相应结果进行对比。结果表明(如图2所示),当α=1,α0=0,α1=0时,结果吻合较好,有微小差异是由于数值计算方法的不同引起,其中最大偏差为5.88%,平均偏差为3.26%。从而进一步验证了本文计算结果的正确性和合理性。
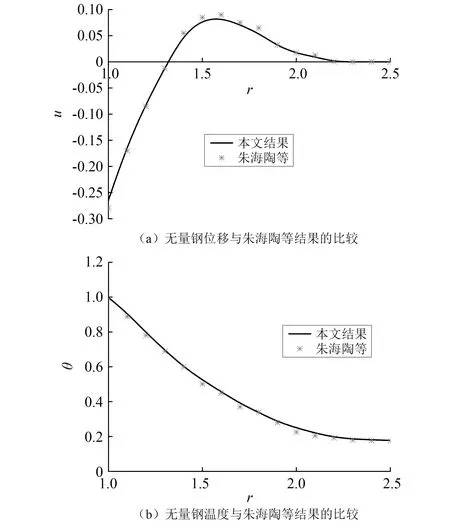
图2 无量纲量与朱海陶等研究结果的比较Fig.2 Comparison between the non-dimension physical variables results in this paper and those in zhuhaitao,et al
为分析温度、位移、径向应力和环向应力随时间t、分数阶系数α和黏弹性松弛时间因子α0和α1的变化规律,计算时考虑了两个时间,即t=0.2,t=0.25,三个不同分数阶系数和黏弹性松弛时间因子α,α0和α1,分别是α=0.1,α=0.5,α=1;α0=0,α0=0.06,α0=0.18;和α1=0,α1=0.09,α1=0.27时几种情况的不同组合。得到了无量纲温度θ、位移u、径向应力σrr和环向应力σφφ的分布规律,如图3~图5所示。当α0=0,α1=0时,黏弹性模型就可以退化成为弹性模型;当α=1时,分数阶模型可以退化成为整数阶模型。
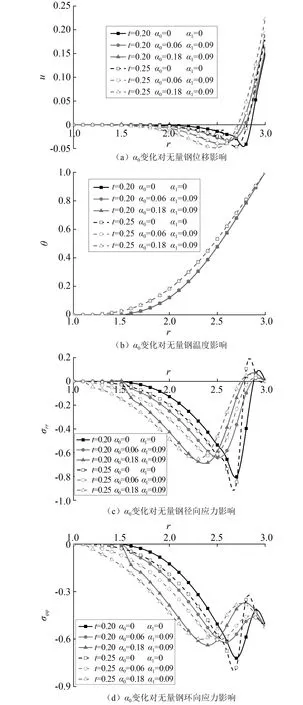
图3 α0变化对各无量纲量的影响Fig.3 Influence of different α0 on non-dimension physical variables
图3描述了热冲击时,黏弹性松弛时间因子α0变化对无量纲温度θ、位移u、径向应力σrr和环向应力σφφ的影响。文中正值表示介质处于膨胀状态,负值表示介质处于压缩状态。图3(a)是中空圆柱中的位移分布图,由于柱体受到热冲击,外表面处发生热膨胀变形,柱体内的位移从膨胀状态到压缩状态动态变化,到内表面时恢复到0。当α0和α1都为0时,曲线在压缩区域的峰值分别在r=2.6和r=2.7处出现。同一作用时间下,随着α0增大,曲线峰值向内移动,这主要是由于黏弹性介质的迟滞作用引起的,黏弹性松弛时间因子α0对位移的影响主要在柱体外表面到柱体内外表面之间处最为明显,当r=1.75时,几条曲线基本重合并衰减为零,扰动基本消失。此外,对于弹性介质而言,作用时间增大使得曲线压缩区域的峰值向内移动,但数值差异不大,而对于黏弹性介质而言,作用时间仅对曲线峰值的幅值大小有微弱的影响,而对峰值的位置影响不大。
图3(b)是中空圆柱的温度变化图,由于柱体外侧受到热荷载作用,热扰动区域从柱体外表面向内部迁移,且温度从1~0依次减小。黏弹性松弛时间因子α0对温度的变化影响不大,随着作用时间的增大,温度衰减速度变快,扰动深度向柱体内部延伸。
图3(c)和图3(d)分别是径向应力和环向应力分布图。图3(c)中径向应力在柱体内外表面处均为零,并随着径向深度增大,应力先表现处压缩状态,直到r>2.6后慢慢进入膨胀状态。随着黏弹性松弛时间因子α0增大,曲线在压缩区域的峰值向柱体内径方向移动,产生明显的滞后现象。不考虑黏弹性时,曲线在压缩区域峰值基本在r=2.7时出现,而在膨胀区域的峰值出现的位置则有明显的不同。
图3(d)中在热冲击作用下,环向产生压应力,同一作用时间下,黏弹性松弛时间因子α0增大使得曲线峰谷值均向柱体内径方向移动,谷值处尤为明显。考虑黏弹性松弛时间因子作用时,不同时间的曲线谷值位置差异很大,但幅值比较接近,不考虑黏弹性松弛时间因子的情况则反之。而对于曲线峰值而言,考虑黏弹性时间因子的曲线峰值大小和位置都相对接近,不考虑黏弹性松弛时间因子的则反之。
在图3(c)和图3(d)中,当作用时间t=0.2时,径向应力和环向应力的三条曲线在1≤r<1.5的区域内基本都是零,随着作用时间增大,这个现象逐渐消失,说明其扰动向柱体内部延伸。
综上所述,作用时间对所有物理量均有明显影响,而黏弹性松弛时间因子则对无量纲温度外的所有物理量均有明显影响。
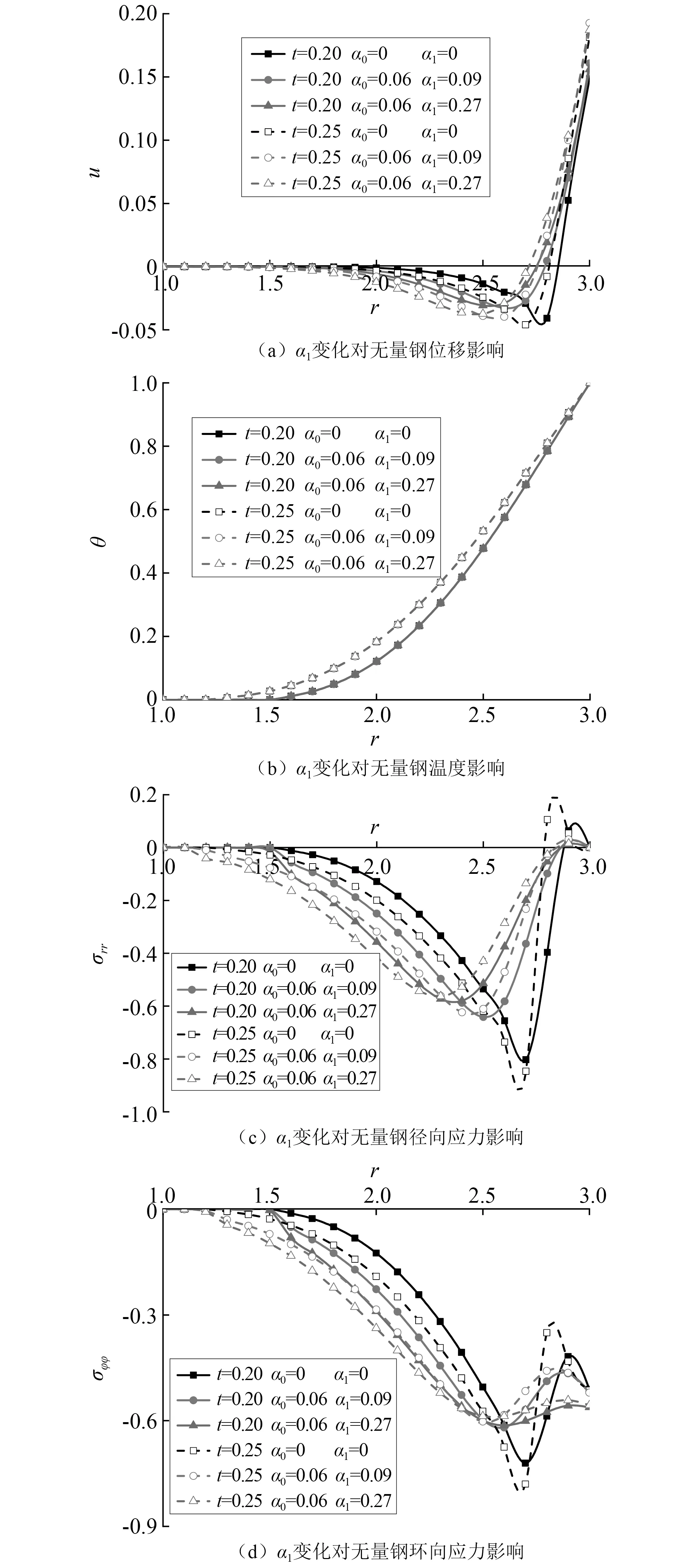
图4 α1变化对各无量纲量的影响Fig.4 Influence of different α1 on non-dimension physical variables
图4描述了热冲击时,黏弹性松弛时间因子α1变化对无量纲温度θ、位移u、径向应力σrr和环向应力σφφ的影响。图4(a)是中空圆柱中的位移分布图,曲线分布趋势与图3(a)黏弹性松弛时间因子α0变化时类似,但没有α0变化时影响明显。不同的是,α1变化不仅对曲线峰值出现的位置有一定的影响,而且还影响了其幅值的大小。图4(b)与图3(b)类似,黏弹性松弛时间因子α1对温度的变化影响不大。图4(c)和图4(d)分别是径向应力和环向应力分布图。黏弹性松弛时间因子α1对径向应力的影响明显,与图3(c)不同的是,随着α1增大,考虑α1的曲线谷值不仅向着圆柱内表面方向移动,数值也在逐渐减小。此外,考虑了黏弹性松弛时间因子作用的曲线在膨胀区域的数值非常小,只有微弱的扰动。图4(d)中环向同样仅产生压应力,在不考虑黏弹性松弛时间因子时,曲线谷值明显靠近柱体外表面,并且更大一些。考虑黏弹性松弛时间因子作用时,随着α1增大,曲线谷值大小和位置都非常接近。当α1=0.27时,曲线的峰谷值基本不太明显,这主要是黏滞性使得曲线的增大和衰减速度明显减慢造成的。
综上,由考虑两种不同黏弹性松弛时间因子的两组图可知,黏弹性松弛时间因子α0和α1对无量纲温度外的各物理量均有明显的滞后作用,这个现象在曲线的峰值和谷值处最为明显。若仅需计算无量纲温度的分布情况可以不考虑黏弹性松弛时间因子α0和α1,从而简化计算。但是,往往热冲击作用会产生变形、位移和应力,仅考虑温度变化是不够的,因此,研究黏弹性松弛时间因子α0和α1对各物理量的研究是不可忽略的。
图5描述了热冲击时,分数阶系数变化对无量纲温度θ、位移u、径向应力σrr和环向应力σφφ的影响。分数阶系数对无量纲位移的影响最小,图5(a)中,分数阶系数对无量纲位移的影响主要体现在曲线峰值及其附近区域。当r<1.5后,热冲击所产生的变形和位移都很小了,这是分数阶系数变化对其影响也是一个很小的值,即可忽略其影响。随着分数阶系数增大,曲线峰值逐渐增大。图5(b)是圆柱中的温度分布图,由于热冲击作用在圆柱外表面,热量向内传递并逐渐减小,分数阶系数使得温度曲线衰减明显变慢,这与分数阶微分算子的记忆性有一定的关系。随着作用时间的增大,不同分数阶系数曲线之间的差异明显增大,这个现象在1.75 图5 分数阶系数变化对各无量纲变量的影响Fig.5 Influence of fractional order coefficient variation on non-dimension physical variables 本文基于Ezzat型分数阶双相滞后广义热弹性理论,根据特征值法以及拉普拉斯数值反变换解法对中空均质各向同性黏弹性柱外表面作用有热冲击的问题进行了研究,得到了在相应热冲击下无限长中空柱体无量纲位移、温度、径向应力和环向应力的分布规律。通过对比分析揭示了分数阶系数、作用时间和黏弹性松弛时间因子对所考虑各物理量的影响规律,结论如下: (1) 当r<1.75后热冲击对无量纲位移的扰动基本消失,不同作用时间对扰动深度的影响不大。而对于无量纲温度、径向应力和环向应力,随着作用时间增大,扰动区域向柱体内部延伸。 (2) 黏弹性松弛时间因子α0和α1对无量纲温度外的所有物理量具有明显的影响,主要在曲线的峰值和谷值处有明显的滞后现象,对径向应力和环向应力的影响更为明显,主要体现在1.5 (3) 分数阶系数对所有物理量均有明显影响,主要体现在幅值最大处及周围区域影响最为明显,当r<1.5后,分数阶系数对各物理量的影响基本消失。考虑分数阶系数后,曲线更平滑,除环向应力外的各曲线峰值同样有明显的滞后。此外,本文的研究结果,可对分析具体热弹性行为α时的取值提供一定的理论参考。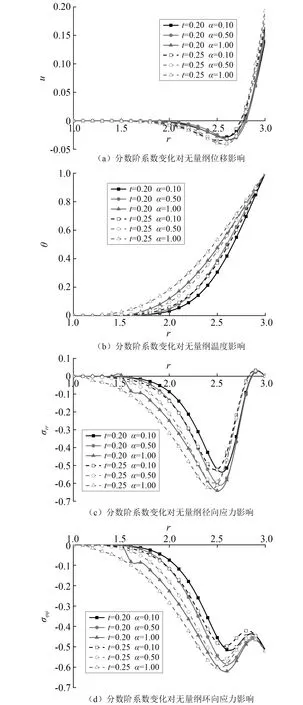
4 结 论
