具有自寻优和协同感知的主轴系统故障数据分析研究
2022-12-01王伟平
王伟平,王 琦,2,于 洋
(1.沈阳工业大学 信息科学与工程学院,沈阳 110870;2.辽宁工业大学,辽宁 锦州 121001)
智能机床是数控机床在智能时代下的新发展。智能机床的故障数据分析能力是衡量其与信息技术融合发展程度的关键。主轴系统是机床最主要的组成部分,其运行平稳性及对故障的感知能力是发挥机床主机自身性能、保证输出精度的基础。
在故障数据分析领域,早些年多以建立数理模型为分析手段。韩秋实等[1]建立了旋转机械信息距离判别函数,并将其应用到对应的故障诊断专家系统模式识别中。陈亚农等[2]基于局部均值分解对滚动轴承故障进行了综合诊断分析。Xi等[3]通过建立一种机床主轴轴承系统的动力学模型进行了故障诊断研究。Berredjem等[4]利用相似性划分的方法研究了从数值数据中自动诱导的模糊规则。程卫东等[5]基于故障特征系数模板对变转速滚动轴承进行了故障诊断研究。此外,贝叶斯网络、决策树等在故障诊断方面也有很多应用。Zhang等[6]通过增强数据独立性进行了基于朴素贝叶斯与决策树的轴承故障诊断。Zhou等[7]利用贝叶斯网络建立了智能故障诊断和故障推理方法。Zhang等[8]将梯度提升决策树应用于轴承故障诊断的数据分析中。
近年来,深度学习算法逐渐成为了数据分析的主流。齐咏生等[9]基于双结构深度学习进行了滚动轴承故障的智能诊断研究。Yang等[10]提出了基于多层双向门控递归单元的注意力机制方法。Pham等[11]建立了一种定义为Mobilenet-v2的CNN模型以优化所需的系统资源。An等[12]通过建立一种端到端的无监督域自适应轴承故障诊断模型实现了域特征和判别特征学习的结合。Huang等[13]提出了一种通过自适应选择特征进行故障诊断分类的注意力机制。Shen等[14]提出将一种改进的层次自适应深度信念网络用于故障诊断。
然而,对设备故障诊断数据的分析研究,数理分析往往仅能就某一局部数据特征进行研究,贝叶斯网络对于相关类型输入变量的诊断辨识能力不足,决策树的稳定性和泛化性相对较差,并且这些算法都难以应对智能化故障诊断下的大数据及复杂多故障时的数据特点分析。而依托深度学习的数据分析,实际在线应对外部干扰时,分析能力有待提升。
针对上述问题,本研究围绕智能机床主轴系统的振动故障数据分析算法展开研究,以提高数据分析体系抑制外部扰动、提升准确度,实现自寻优与多维度协同融合为目标,构建算法。文中以具备识别振动波形数据的波动特征分析、细节时频分析的双路径模块为核心,建立了数据主体辨识环节。为应对在线外部噪声扰动,建立了前置滤噪环节。通过采集电能质量分析仪监控的电流数据,建立了电流分析环节。基于这些环节的建立,在整体算法层面,以强化学习的Q-learning为基础构建了自寻优驱动环节,以D-S证据理论为基础构建了面向整个算法架构的多维度协同感知评估环节。并以凯斯西储大学(Case Western Reserve University,CWRU)轴承数据集和实际机床主轴系统的故障数据,验证了所提方法的优越性、有效性与准确性。
1 数据分析方法研究
1.1 主轴系统故障的特点
机床主轴系统的结构与控制图示如图1所示。
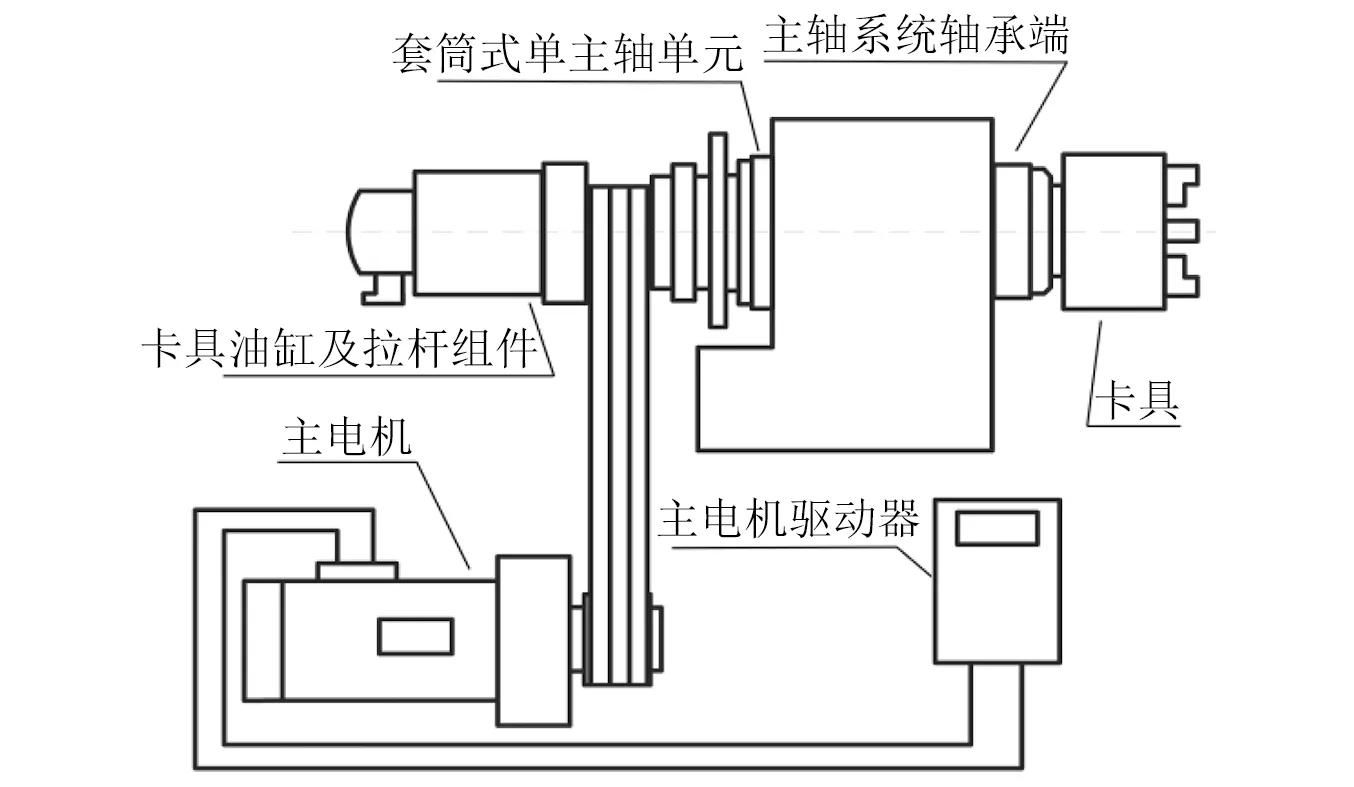
图1 主轴系统结构与控制图示Fig.1 Structure and control diagram of spindle system
机床主轴系统的故障特点归结如下:
(1)故障存在渐变性。即关键回转部件损伤,往往是局部渐变损伤。如主轴轴承内环、外环、滚动体研伤。
(2)故障存在微观变化的特点。如关键接触结构件装配结合面的微观受力变化,导致回转部件运动接触表面的浅层磨损,产生受力不均或固有频率变化。
(3)故障特征研究易受外部环境、工况变化及自身组件的不同轴、抖动、共振等扰动的影响。
(4)故障特征需特定方法才能有效提取,特征提取的质量和数据分析算法的最优设计是解决问题的关键。
1.2 静、动态数据分析研究的特点
静态数据分析,利于算法本身在排除外部噪声、变工况等扰动情况下对研究问题进行深入分析与研究拓展。动态数据分析,研究变工况、外部扰动、多种因素状态共同变化等情况,是面向实际的研究。本文设计提出的离线双路径深度学习模型属于静态数据研究,在线自寻优属于动态研究数据变化过程。
1.3 自寻优与协同感知分析算法的特点
本文算法总体特点如图2所示。
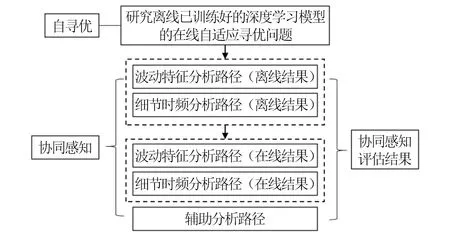
图2 本文算法总体特点Fig.2 The general characteristics of this algorithm
自寻优是指在训练与迭代过程中自主寻找到最有利于数据分析结果产生与优化的方式,具备人工智能的特点,有利于工业实际中复杂问题的研究解决[15]。协同感知,是从多个维度分析一个复杂问题,实现离线、在线、多视角的对多种局部变量分析结果的协同与综合评估。协同感知有利于工业过程分析中多类问题的研究解决[16]。
2 算法原理
2.1 算法模型
本文提出的自寻优与多维度协同感知故障数据分析算法架构如图3所示。它包括前置环节、在线驱动环节、主体辨识环节、电流分析环节、评估决策环节。
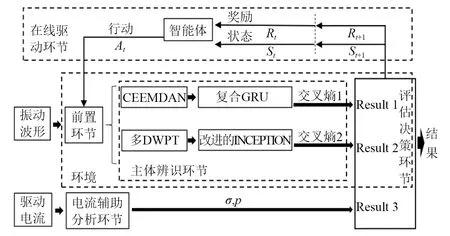
图3 本文提出的自寻优与多维度协同感知算法架构Fig.3 The self-optimization and multi-dimensional collaborative perception algorithm architecture proposed in this paper
2.2 前置环节
前置环节(见图3)是配合在线驱动环节,实现整体算法的在线自寻优。其包含5种小波分解基和3种小波分解层数,在在线驱动环节的驱动下,通过分解与重构效果比较,实现对在线振动信号的最优小波自适应软阈值降噪。前置环节中,使用基于ddencmp函数生成默认软阈值。前置环节与在线驱动环节一起为主体辨识环节提供降噪预处理后的振动波形数据,以提高主体辨识环节的最终辨识效果。
2.3 在线驱动环节
在线驱动环节是文中算法(见图3)的驱动核心,是指由智能体和环境共同构成的环节。在线驱动环节与前置环节共同实现图3算法整体的在线自寻优。在线驱动环节的设计,主要基于强化学习的思想。将强化学习应用于故障诊断之中有利于故障诊断的自适应智能化发展[17]。
强化学习模型一般分为Q-learning、DQN、DDPG。与DQN、DDPG相比,Q-learning更适合于无策略更新环境,文中算法的重点在于寻优在线分析环境,为决策环节提供数据特征变化,因此使用Q-learning更为合理。
2.3.1 在线驱动环节中强化学习算法设计
由图3,在线驱动环节的强化学习算法设计:
(1)环境——包含前置环节、环境的其他环节(主体辨识环节、评估决策环节)。
(2)奖励——环境对于在线外部输入振动波形的辨识评估结果。由评估决策环节最终给出即时奖励。
(3)状态——状态是指智能体的Q表(见表1)中所存储的前置环节中包含的5种不同种类小波基及3层分解层数的对应位置状态:1#~15#。其中,1#~15#为15个容量各为22的存贮器,用来存放10轮在线评优中环境返回的即时奖励值及各自10轮奖励值的最终总值(双路径)。表1中,5种小波基的选取是充分考虑降噪常用的并已自行验证筛选效果最好的小波基,1~3层3种小波分解重构层数的选取,是在相关反复多次分析研究的基础上,基于既要达到滤除噪声的目的,又要尽可能减少原有信号的损失的目标所确定的。
(4)行动——智能体每次顺序调用Q表中一种状态。
(5)策略——在线驱动环节的强化学习属于无策略顺序调用,即依表1内的1#~15#状态顺序依次调用。
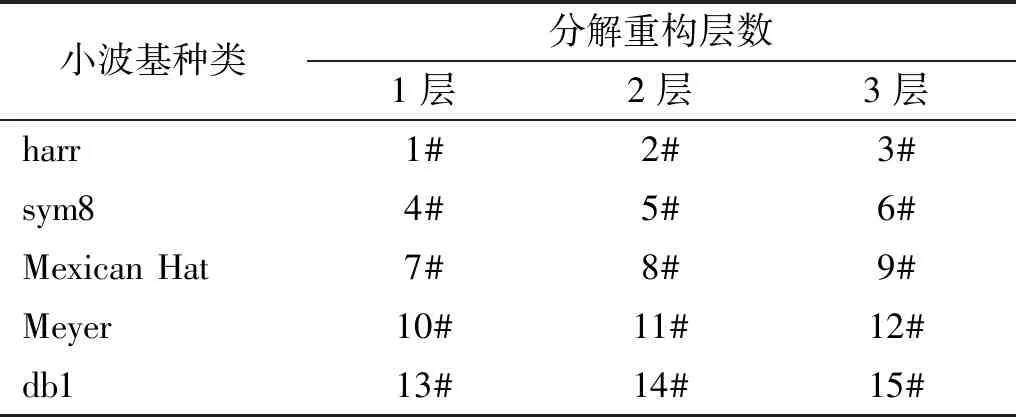
表1 小波基和分解层数(Q表)Tab.1 Wavelet basis and number of decomposition layers(Q table)
2.3.2 基于强化学习Q-learning的算法实现步骤
根据式(1)进行Q表的更新,其中st,at表示当前的状态和行为,st+1,at+1表示st的下一个状态和其对应的行为,γ是学习率,其取值范围是[0,1)。
Q(st,at)=R(st,at)+γ·maxat+1{Q(st+1,at+1)}
(1)
实施步骤:
步骤1设定参数γ=0,即Q表的数值取仅决于当前环境反馈的对应奖励值R;
步骤2令初始值Q=0;
步骤3对于每个迭代轮次,按表1,s的取值由1#依次取到15#,返回即时奖励值,记录到Q表的对应位置。
2.4 主体辨识环节
该环节提出了双路径深度学习算法模型(见图3)。深度学习是目前研究故障与风险评估的主流方法[18]。提出的双路径分别为由自适应噪声完备集成经验模态分解[19]与复合GRU模型(CEEMDAN+复合GRU)构成的“波形波动特征分析路径”,及由多离散小波包分解系数与改进的INCEPTION网络(多DWPT+改进的INCEPTION)构成的“波形细节时频分析路径”。算法设计目的是考虑从波形的波动包洛特性和细节时频分析特性两个维度,实现对振动波形数据特征的最大程度感知,提高辨识准确度。该部分采用先离线训练模型参数,然后对模型结构和模型参数(权重、偏移量等)进行固化,再应用到在线故障辨识中,缓解在线数据集贫乏问题。在强化学习驱动前置环节完成自适应噪声滤除后,主体辨识环节发挥进一步辨识数据特征作用。
2.4.1 波动特征分析路径
(1)基于CEEMDAN的波形特征提取
如图4所示,该路径采用CEEMDAN进行特征提取。CEEMDAN算法是在经验模态分解(empirical mode decomposition,EMD)基础上进行改进,添加逐级减小的白噪声,有效抑制了模态混叠问题,分解效率更高,特征提取效果更好。因此,本文使用CEEMDAN算法。
(2)波动特征辨识算法模型设计
门控循环单元网络(gate recurrent unit,GRU)是深度学习中循环神经网络的一种,它较长短期记忆循环网络(long short-term memory,LSTM)的结构更加简单,并且训练速度快于LSTM。本文设计了改进的复合GRU模型结构。如图4所示,它由5个单GRU模型和1个全连接层,1个softmax层构成。CEEMDAN分解后得到的IMF1,IMF2,IMF3,IMF4,IMF5分量同时作为特征数据,输入到由复合GRU构成的模型。该模型设计充分利用GRU模型对于连续数据的感知递推记忆特点,与CEEMDAN配合,在提高辨识准确率的同时,增大了各分量类间差异的辨识能力。
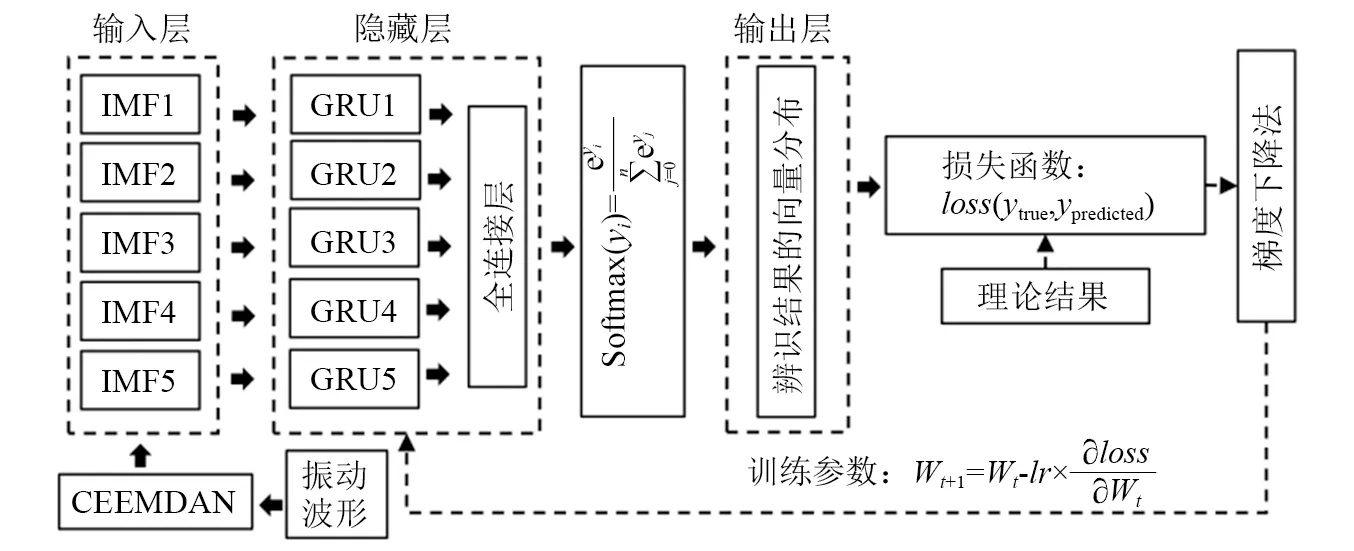
图4 波形波动特征分析路径Fig.4 Waveform fluctuation characteristic analysis path
2.4.2 波形细节时频分析路径
根据细节时频分析路径的研究需要,提出设计了“多DWPT+改进的INCEPTION”算法模型,如图5所示。
(1)离散小波包变换(discrete wavelet packet transform,DWPT)特征提取
离散小波包变换是典型的波形特征提取方法。本文提出使用4个小波基(db1,db3,sym2,sym8),进行4层离散小波包变换。对输入的波形数据,以1 024点为一个样本,进行小波包分解。将分解后的系数以节点序号为行号,形成4个16×16维的分解系数组合矩阵,作为特征提取结果送入到改进的INCEPTION模型,见图5。这里使用db1,db3,sym2,sym8小波基,是经过研究比较,确定这4种小波基对于本文所研究的振动波形的特征提取效果最好,采用4层离散小波包变换获得的特征节点数既保证了对于数据特征有效提取的需要,又可有效降低后续深度学习网络的数据输入量。
(2)改进的INCEPTION辨识网络
INCEPTION是一种高效精准的深度学习卷积神经网络模型,模型的训练难度适中,具备多种卷积核并行处理的特点,模型的稳定性好,对于多DWPT分解的特征系数矩阵的辨识能力好。本文对其进行了改进:在基本INCEPTION的基础上,将原来5×5卷积核替换为1×2,2×1,1×2,2×1卷积核,将3×3卷积核替换为1×3,3×1卷积核,如图5所示。
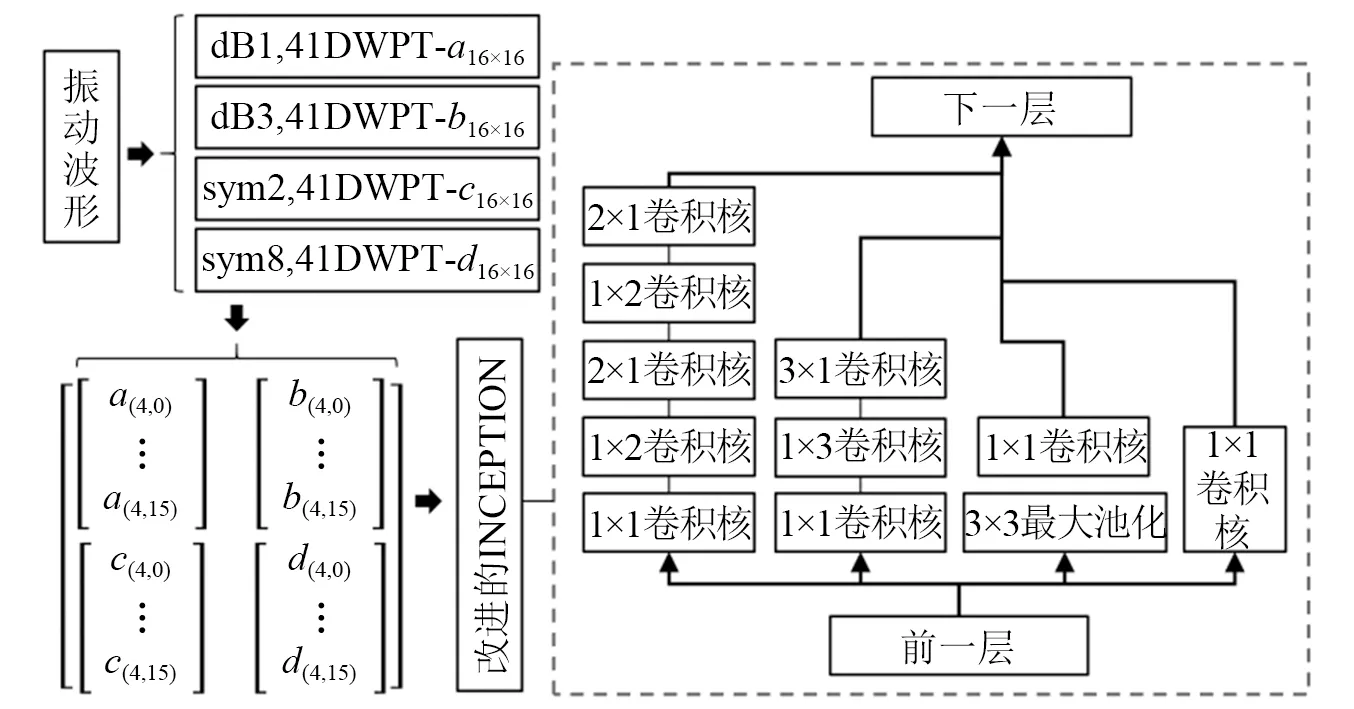
图5 波形细节时频分析路径Fig.5 Waveform detail time-frequency analysis path
2.5 电流辅助分析环节
电流分析环节在整个算法中起辅助分析作用(见图3)。该环节使用电能质量分析仪采集主电机驱动器输送给主电机的电流数据作为特征数据,起到粗精度辅助分析的作用(如图6所示)。

图6 基于测试电流的故障辅助分析Fig.6 Fault aided analysis based on test current
在空载测试研究中,主轴支承轴承是主轴系统主要的磨损变化故障源,主轴系统出现故障时,主电机驱动器基于PID控制会对主轴系统传递到主电机的故障扰动做出及时调节,这种调节通过输出电流的变化实现。这里提取主轴系统平稳运行时段的驱动器输出电流波形数据的标准差和脉冲因子作为特征值。公式如式(2)(标准差σ)和式(3)(脉冲因子p)所示。
(2)
(3)
标准差用来反映数据集的离散程度,这里为主轴系统在平稳运行区段中对电流波形幅值整体变化均值的反映。脉冲因子是用来表征信号中峰值冲击特征的量,从式(3)的构成,可知此处脉冲因子的应用,是主轴系统在平稳运行区段中对电流波形峰值突变状态的反映。这里通过多次测量计算该台机床在正常工作时和出现故障时对应的标准差及脉冲因子,进而分别确定标准差和脉冲因子的故障阈值。注:不同机床之间由于装配条件和组件配合精度的差异,标准差和脉冲因子的故障阈值存在差异,需要依照这里提出的方法,建立各自的特征数据集。但对于同一台机床,其标准差和脉冲因子的故障阈值,可以通过研究获得。本文是对所研究的故障机床自身的正常态和故障态进行算法验证,不进行不同机床间的横向比较。
2.6 评估决策环节
由图3,评估决策环节是在线数据分析的决策环节。本环节一方面是汇总在线“主体辨识环节”对振动传感器所检测波形的分析辨识结果(即Result 1、Result 2的辨识结果),并向智能体返回即时奖励值;另一方面是基于Result 1、Result 2的奖励值结果结合电流分析环节Result 3的结果,使用D-S证据理论的合成规则计算出主轴系统故障的状态评估结果(见图7)。图7的具体分析运算过程在后文对应进行了详细举例说明。
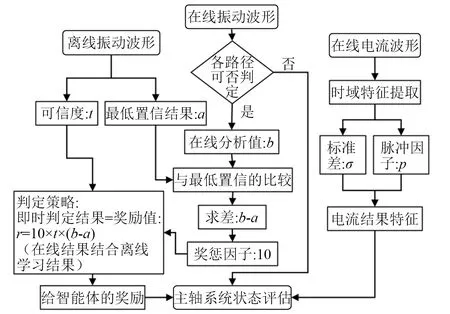
图7 决策环节离线在线结果分析Fig.7 Analysis on the relationship between offline and online results of decision-making links
D-S证据理论在依托信任度进行多证据融合方面很有优势[20]。其合成规则是采用正交和计算两种或多种判据的信任匹配函数。如识别架构Ω存在证据E1和E2,对应的信任配比是e1和e2,Mi和Nj是焦元,可得合成规则
(4)
式中,V为冲击系数,越大表明证据间冲击越大。
3 算法比较
为验证本文提出的数据分析算法的优势,这里基于CWRU轴承数据集对整个算法的核心部分—主体辨识环节(见图3)的优势进行对比验证。CWRU轴承数据集是基于试验台获得的数据集,其对应的试验台由电机、扭矩传感器和功率计构成,通过采集电机支撑轴承的驱动端和风扇端的轴承振动信号而获得轴承振动信号数据集,其中轴承的故障是使用电火花加工技术在轴承对应位置上加工出直径不同的点蚀所致。CWRU轴承数据集在轴承振动信号研究领域,获得广泛认可,被用于验证很多算法研究,具有通用性。这里使用其对本文所提出的算法主体部分进行验证评估,所选的数据如表2所示。

表2 正常数据和故障数据Tab.2 Normal data and fault data
研究中对表2的数据,采用了数据增强技术—重叠采样。提取的数据每类100组,共1 000组。其中700组作为训练集,300组作为验证集。
3.1 波动特征分析路径内所提算法优势对比
将本文提出的“CEEMDAN+复合GRU”模型(算法1)与“CEEMDAN+LSTM”(算法2)同步进行训练验证,结果见表3和图8。可以看出算法1的验证集准确率均值优于算法2,所用时间比算法2更少。
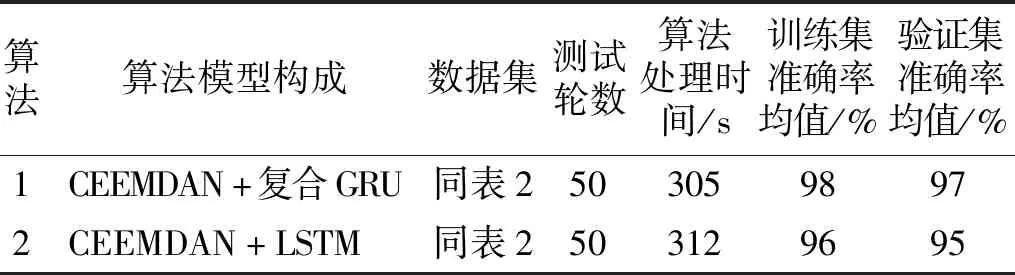
表3 验证集准确率结果对比Tab.3 Comparison of accuracy results of validation set
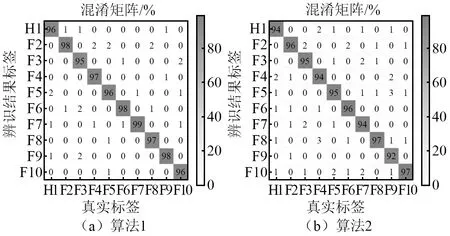
图8 验证集准确率混淆矩阵Fig.8 Accuracy confusion matrix of verification set
3.2 细节时频分析路径内所提算法准确率对比
3.2.1 准确率对比
将本文提出的“多DWPT+改进的INCEPTION”模型算法(算法3)与“单DWPT+基本INCEPTION”模型(算法4)进行比较。选用数据及结果对比如图9、图10和表4所示。

图9 算法3的辨识效果Fig.9 Identification effect of algorithm 3
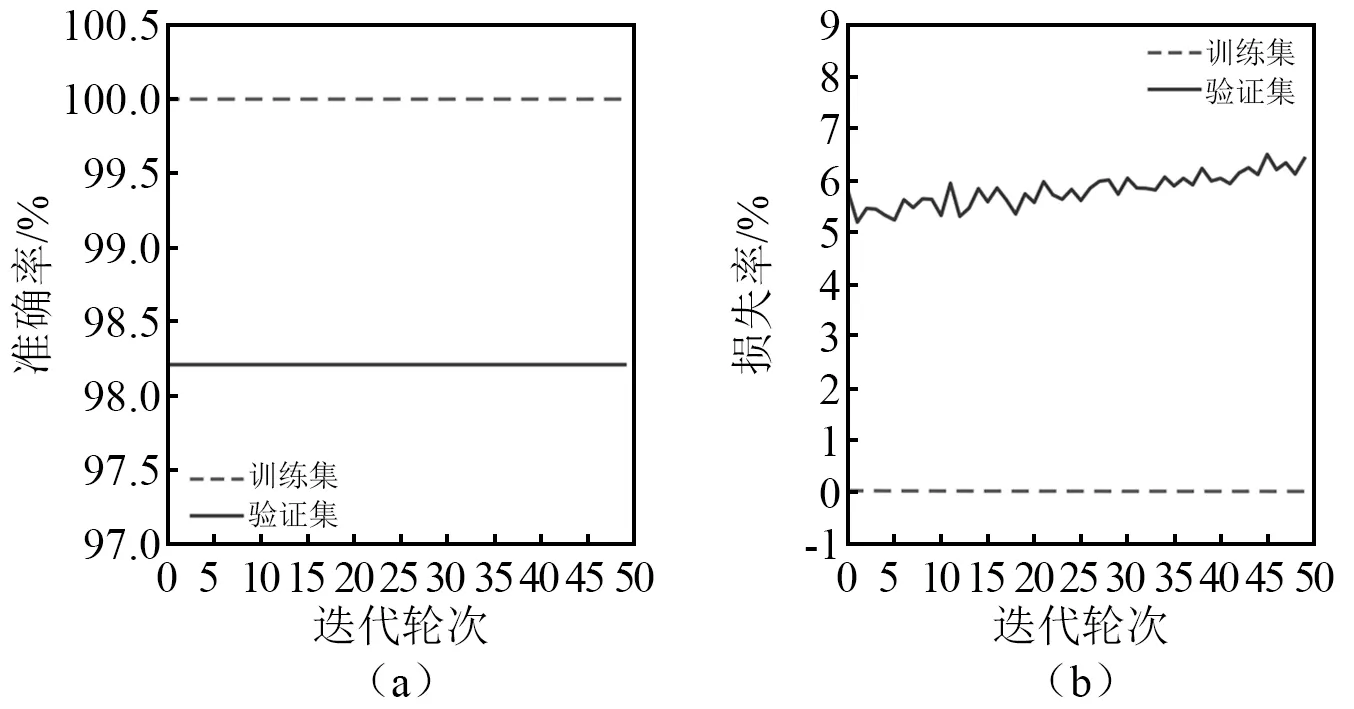
图10 算法4的辨识效果Fig.10 Identification effect of algorithm 4

表4 验证集辨识准确率结果Tab.4 Identification accuracy results of verification set
图9、图10对比分析了准确率和损失函数情况。从图上可看出本文提出的“多DWPT+改进的INCEPTION”模型算法的分类辨识效果优于“单DWPT+基本INCEPTION”算法,数据汇总见表4。
3.2.2 辨识准确性十折交叉验证
将本文提出的“多DWPT+改进的INCEPTION”模型(算法3)和“多DWPT+AlexNet”等模型训练好后,进行验证集十折交叉准确率验证比较。从图11和表5的结果可以看出,算法3明显最优。
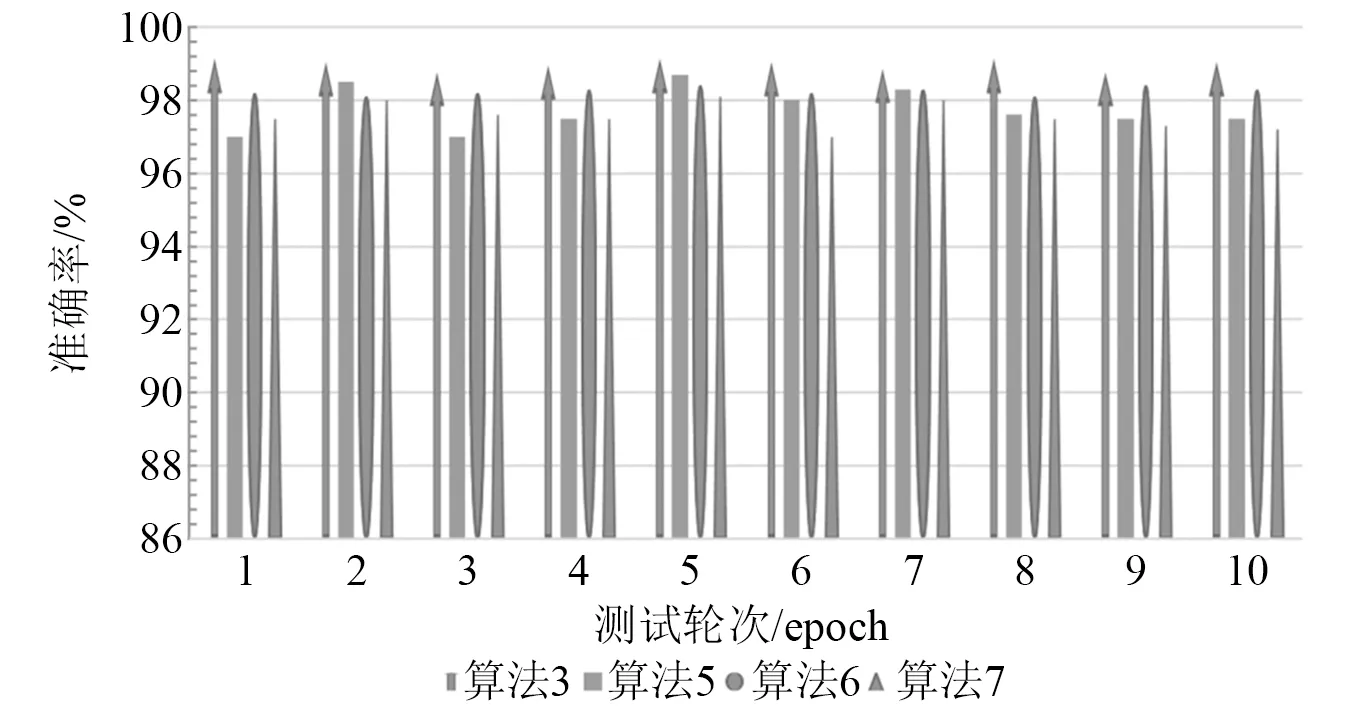
图11 验证集十折交叉准确率对比Fig.11 Comparison of ten fold cross accuracy of verification set

表5 验证集十折交叉准确率结果对比Tab.5 Comparison of accuracy results of verification set
4 实际验证
4.1 实际机床的主轴系统故障
本研究选取一台标准型40规格的智能流量型卧式数控车床,验证文中提出的故障数据分析算法(见图3)。对实际机床主轴系统故障的验证,是在实际外部扰动下,面向算法多环节(在线驱动环节、主体辨识环节、电流环节等)的专有数据验证,是本文验证研究的主要内容。与基于试验台的CWRU数据集验证相比,更具有专有性、针对性特点,加之是对算法整体各环节的全面验证,其结果可验证算法整体各环节对本文研究对象进行实际故障辨识的有效性与实用性。
该机床在加工零件内表面时存在颤振振纹(如图12所示)。在排除进给轴、刀具、切削参数、装卡等因素后,将故障诊断研究的重点放在机床主轴系统上。

图12 加工件内沟槽处出现加工颤振振纹Fig.12 Machining chatter marks appear at the groove in the machined part
4.2 数据采集与验证方案
如图13所示,在加工区主轴系统轴承侧,安装B &K振动加速度传感器,采集主轴输出端的振动状态特征。

图13 振动传感器的安装Fig.13 Installation of vibration sensor
空载条件下,采集该台故障机床在主轴转速2 000 r/min时主轴单元轴承侧的振动数据。采用FLUCK电能质量分析仪,同步采集主电机驱动器输出端的输出电流波形数据(如图14所示)。

图14 使用电能质量分析仪采集主电机驱动器的电流数据Fig.14 The power quality analyzer is used to collect the current data of the main motor driver
4.3 对本文所提算法的实际验证
4.3.1 主体辨识环节的离线训练
从该流量型机床的历史检测数据中筛选出主轴系统轴承侧振动检测数据并汇总,如表6所示。
使用表6数据,离线训练文中提出的“CEEMDAN+复合GRU”波动特征分析算法模型,再在训练好的该离线模型上,使用验证集进行验证,获得交叉熵最低判定值0.75(对应的分布是(0,0.75,0.09,0.16),对应的判定标签值为(0,1,0,0))。同理,采用提出的“多DWPT+改进的INCEPTION”时频分析路径算法进行离线训练,判定结果交叉熵最低为0.79,数据汇总如表7所示。
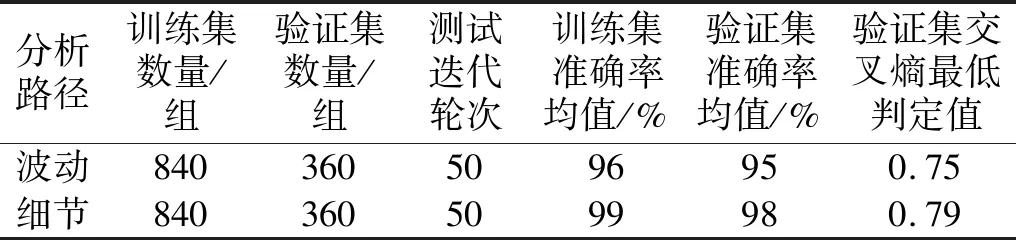
表7 双路径离线数据Tab.7 Dual path offline data
4.3.2 在线自寻优
(1)小波去噪重构效果对比
图15是在2 000 r/min时,对4.2节故障机床采集到的含有干扰的振动波形进行的不同小波基去噪效果对比。
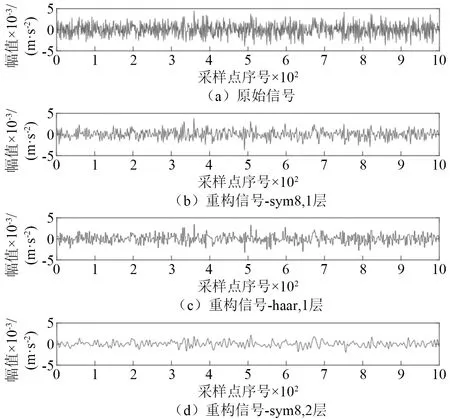
图15 2 000 r/min时不同小波分解重构效果Fig.15 Reconstruction effect of different wavelet decomposition at 2 000 r/min
图15(b)~图15(d)分别是采用1层sym8、1层haar、2层sym8小波基,对波形数据进行的去噪效果对比。可以发现采用不同小波基和分解重构层数,对波形的预处理效果差异明显。这说明在本文算法架构(见图3)的前置环节中,寻找出最优降噪效果对于提升现场实际波形数据辨识分析效果的必要性。
(2)基于强化学习Q-learning的在线自寻优
根据文中2.3节、2.4节提出的在线学习方法,按照图7的分析策略,采用4.3.1节训练好的模型(模型效果数据见表7),对4.2节故障机床主轴系统在2 000 r/min测得的振动数据,进行在线辨识,分析获得了路径1和路径2每次迭代的即时结果,即环境为智能体提供的即时奖励,相关过程数据举例如表8所示。
表8为主体辨识环节进行某次数据分析时的在线分析策略,该策略中“即时判定结果=奖励值:R=10×t×(b-a)”充分考虑了离线训练结果对于在线训练的影响,使每次判定都综合了离线模型的结果数据(可信度),从而增加了在线辨识本身的鲁棒性和全面性。
(3)双路径主体辨识环节在线分析
在离线训练好双路径主体辨识模型后,固化模型的权重、偏移量等参数,再应用到在线故障辨识中(参见图2)。使用图3的在线驱动环节算法进行10轮迭代(每轮1#~15#,15次),每轮每次都按照表8的方式计算环境产生的对应表1各位置的即时奖励值,最终计算表1各位置的10次奖励总值。
4.3.3 多维度数据协同感知
对于电能质量分析仪采集的4.2节故障机床在空载测试时平稳运行时段的同步电流,采用式(2)和式(3)对平稳运行段电流波形数据进行计算,得到标准差结果σ=0.007 9,超过对应阈值0.005,脉冲因子结果p=0.020 5,超过对应阈值0.015。此处标准差故障阈值和脉冲因子故障阈值是按照2.5节所述对于该台故障机床长期研究后确定的。由此处标准差和脉冲因子的结果都超过阈值的结果,结合图6,考虑出现一定程度的损伤加剧。但对于主轴支承轴承的内环、外环、滚动体损伤无法进一步辨识,故电流分析路径仅能发现是否正常,因此此环节对于主轴轴承内环、外环、滚动体及不确定性故障的判定可能性占比各为25%,需借助主体辨识环节进一步辨识故障类别。
4.3.4 故障数据多维度协同感知评估
这里对汇总后的各路径结果进行基于D-S证据理论的多维度协同感知评估计算。按表1顺序,由Q-learning驱动整个在线分析网络,按图7和表8策略进行自寻优,提取Q表中各路径、10轮寻优总奖励值(如图16所示)及10轮对应的交叉熵概率分布,进行汇总。确定:采用sym8小波基进行1层分解重构,获得的总奖励值最高,其对应的最大交叉熵辨识概率分布如表9所示。
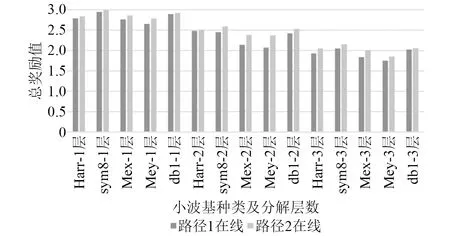
图16 在线奖励总值汇总Fig.16 Total online rewards

表9 最大交叉熵对应的数据Tab.9 The corresponding data of the maximum cross entropy
关于表9的4#数据,L1、L2路径的不确定度θ由离线模型的可信度t(见表8)与1的差值确定(例L1:1-95%=0.05)。在此基础上,各路径分别与本路径不确定度进行归一化,路径1(L1)的辨识概率分布结果为(0,0.095,0.085 5,0.769 5),路径2(L2)的辨识概率分布结果为(0,0.098,0.049,0.833)。基于式(4)进行计算:
(1)各路径证据信息
m1(正,内,外,滚,θ)=(0,0.095,0.085 5,0.769 5,0.05)
m2(正,内,外,滚,θ)=(0,0.098,0.049,0.833,0.02)
m3(正,内,外,滚,θ)=(0,0.25,0.25,0.25,0.25)
(2)信任值乘积之和
m’(正)= (m1(正)+m1(θ))(m2(正)+m2(θ))(m3(正)+m3(θ))-(m1(θ))(m2(θ))(m3(θ))=0,同理:m’(内)=0.008 3;m’(外)=0.004 4;m’(滚)=0.349 3;m’(θ)=0.001 8
(3)归一化处理
1-V=m’(正)+m’(内)+m’(外)+m’(滚)+m’(θ)=0.363 8
(4)最终结果
m(正)=m’(正)/(1-V)=0;同理:m(内)=0.022 8;m(外)=0.012 1;m(滚)=0.960 1;m(θ)=0.004 9
根据上述运算结果,m(滚)=0.960 1,即最终确定该机床主轴系统故障结果:主轴系统轴承滚动体损伤。
4.4 故障确认验证
在使用文中提出的算法计算确认故障后,最终通过拆卸机床主轴单元,发现该台机床主轴轴承滚动体已烧坏、变色,见图17(a)。图17(b)是作为对比的同型号正常机床的主轴轴承滚动体。此结果也验证了文中算法对于该机床主轴系统故障诊断的准确性。

图17 主轴轴承滚动体Fig.17 Spindle bearing rolling element
5 结 论
本研究提出了具有自寻优和多维度协同感知的主轴系统故障数据分析算法。
(1)对于故障振动波形数据,从离、在线维度,提出建立了具有双路径特征的主体辨识环节,提出建立了具备自寻优特点的在线驱动环节与前置环节。在此基础上提出将双路径离、在线维度的自寻优结果与电流波动状态的辅助故障分析特征进行融合,通过对融合结果的协同评估,实现了整个自寻优和多维度协同感知算法架构。
(2)在构建上述算法架构模型的过程中,提出了由CEEMDAN与复合GRU模型构成的波动特征分析路径,提出了由4个小波基叠加的波形特征提取组合矩阵与改进的INCEPTION模型构成的细节时频分析路径。基于CWRU轴承试验台数据集验证了该双路径(即主体辨识环节)故障辨识的有效性和优越性。
(3)基于实际机床主轴系统的故障数据,验证了提出的算法架构各环节故障辨识的有效性与实用性。对于算法各环节实际故障辨识结果,提出了基于D-S证据理论的离、在线多维度结果融合方法,以0.960 1的协同评估概率量化出了实际机床主轴系统的具体故障原因。
(4)本文为机床主轴系统等关键组件,在实际智能化故障辨识研究中,遇到的实际噪声扰动多、故障辨识准确度要求高、在线数据集贫乏、故障特征判别维度多等问题的相关研究,提供了借鉴。
