多尺度一维卷积神经网络的风机基础螺栓松动智能检测

陈仁祥，徐培文，韩坤林，曾 力，王 帅，朱玉清

(1.重庆交通大学 交通工程应用机器人重庆市工程实验室，重庆 400074；2.招商局重庆交通科研设计院有限公司,重庆 400067)

风机作为工程中主要通风装置，在实际工程中，其工作环境恶劣、连续长时间运转，且受自身质量影响，容易致使风机安装基础螺栓松动，影响风机正常工作和通风安全，甚至造成重大安全事故[1]。因此，对风机基础螺栓松动进行有效检测具有重要意义。

目前，国内外主要通过3种方法对风机基础结构进行检测：①机械式加载检测其承载负荷；②采用无损探伤的方法进行结构稳定性检测；③通过振动信号进行健康性检测。然而，机械式加载本身具有一定的破坏性，容易造成预埋件的钢板被拉出、钢板与拱顶混凝土脱离等问题。无损探伤对风机结构无损伤，但只能检测基础表面附近损伤，且无损探伤设备对安装环境要求较高。振动传感器的安装、振动信号的采集更为方便，且对风机结构无损伤，对环境要求不高，更适合于风机基础结构检测。

近年来，国内外学者通过振动信号对风机基础结构检测进行了广泛研究。韩坤林[2]利用LLTSA(linear local tangent space alignment)算法对人工提取24维振动混合域特征参数进行特征约简，结合最近邻分类器(K-nearest neighbors classifier，KNNC)实现风机基础健康检测。陈仁祥等[3]结合敏感特征与流行学习约简构造风机基础连接螺栓松动程度低维特征集，通过加权最近邻分类器(weight K-nearest neighbors classifier，WKNNC)实现风机基座螺栓松动诊断。以上方法在同转速下效果不错，但这些方法需要依靠人工提取振动信号特征，依赖于大量信号处理技术和专家知识与经验，难以利用人工提取的浅层特征对原始信号进行全面准确刻画，更难以解决不同转速下风机基础螺栓松动检测问题。

卷积神经网络(convolution neural network，CNN)作为经典的深度学习模型，其局部感知、权值共享及下采样技术等思想可有效降低网络的复杂度，具有强鲁棒性和容错能力[4],在故障诊断和健康检测领域得到了广泛应用。Zhang等[5]将轴承一维振动时域信号转化为二维图像作为输入，利用CNN进行训练和故障分类。Wen等[6]提出一种将时域信号转化为二维图像的方法，结合CNN实现轴承和离心泵的故障诊断。卷积神经网络处理的数据一般是二维的，而鉴于原始振动信号自身一维性的特点，使用一维卷积神经网络模型可避免将一维振动信号转化为二维图像的过程，在处理一维信号上更具备优势[7]。安晶等[8]通过改进的一维卷积神经网络对旋转机械进行了故障识别。周奇才等[9]以原始信号作为输入，通过一维卷积神经网络对旋转机械进行了故障识别。以上方法均取得不错效果,但单层卷积层如果只使用单一尺度的卷积核容易忽略其他精细度的特征，导致提取的特征表达信息不够完整[10],影响特征学习效果，且悬挂风机往往工作在不同转速下，单一尺度卷积核不利于学习转速变化下振动信号特征。

目前，多尺度一维卷积神经网络以其强大的特征学习能力应用在复杂的目标识别等领域。郭晨等[11]运用深度多尺度一维卷积神经网络实现雷达舰船目标识别。吴俊等[12]通过多尺度一维卷积神经网络实现光纤振动事件识别。多尺度一维卷积神经网络可从复杂的信号中提取出不同精细度的特征为从风机基础振动信号(特别是变转速工况下)的处理提供了解决思路。

鉴于以上问题，提出多尺度一维卷积神经网络的风机基础螺栓松动智能检测方法。以原始振动时域信号作为输出，最大程度保留原始信号特征；通过设计多尺度卷积运算，提取到不同精细度的特征，实现风机基础时域信号特征精细化表征，并与模式识别有机融合在一起，形成了端到端的风机基础螺栓松动智能检测，解决了风机基础结构振动信号(特别针对存在转速变化情况)特征提取难的问题。通过在稳定转速和变转速下对风机基础螺栓松动检测试验，证明了所提方法的可行性和有效性。

1 多尺度一维卷积神经网络

1.1 多尺度卷积层

从学习局部感受野特征信息角度考虑：不同尺度的卷积核能提取不同精细度的特征。卷积核的尺度越小，提取的特征越细致，对于高频特征较敏感；尺寸较大的卷积核能获取更大的感受野，可以学习更长时间范围的信息，即信号中存在的低频特征。因而融合不同尺度卷积核的优势，通过设置不同尺度卷积核进行卷积运算，可避免单一尺度卷积核对不同精细度特征的忽略，将信号特征进行精细化表征，使特征信息表达更充分。

多尺度一维卷积神经网络结构如图1所示，多尺度卷积层包含n个并行的卷积层，每个卷积层使用不同尺度的一维卷积核对输入信号进行不同尺度的卷积，实现不同精细度信号特征的提取。然后对各卷积层所提取特征进行拼接，输出到下一层，如图2所示。

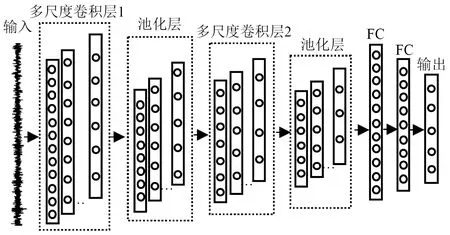
图1 多尺度一维卷积神经网络结构Fig.1 Multi-scale one-dimensional convolutional neural network structure

图2 多尺度卷积层Fig.2 Multi-scale convolutional layer

多尺度一维卷积定义为

(1)

f(x)=max(0,x)

(2)

1.2 池化层

池化层是对上一层数据的缩放映射，通过池化核对输入数据进行子采样，可大幅减少输入数据的空间维度。如式(3)所示

yi=f[βidown(x)+bi]

(3)

式中:down(*)为下采样函数;βi为第i个特征的权值；x对应上一层(卷积层)的输出；bi为第i个特征的偏置。

1.3 全连接层和Softmax多分类器

全连接层中的每个神经元与前一层的所有神经元进行全连接，可以整合卷积层或者池化层中具有类别区分性的局部信息。全连接层后接一个隐藏层，最后由Softmax多分类器完成分类。假设由k类的分类问题，Softmax多分类器的输出可以计算如下[13]

(4)

式中：W和b分别为权重矩阵和偏置值；O为卷积神经网络的最终输出。

2 多尺度一维卷积神经网络的风机基础螺栓松动智能检测方法

所提多尺度一维卷积神经网络的风机基础螺栓松动智能检测方法过程如下：首先，将风机运行时原始振动时域信号作为多尺度一维卷积神经网络的输入，前向传播经交替的多尺度卷积层和池化层将时域信号变换形成精细化分布式特征表达，完成风机基础螺栓松动特征自适应提取；然后，反向传播逐层微调网络参数，建立特征空间到松动状态空间的映射；最终，由Softmax多分类器输出检测结果。整个过程将松动特征自学习与松动识别融合为一个整体，其具体流程如图3所示。

具体步骤如下：

步骤1获取原始振动时域信号，划分训练样本和测试样本；

步骤2以批量方式输入训练样本，设置多尺度一维卷积神经网络结构及其卷积核大小，逐层向前传播获取精细化样本特征，在输出层获取实际松动状态类别，计算期望输出与实际输出的误差；

步骤3将误差反向传播，逐层微调网络参数；

步骤4重复步骤2、步骤3，直到将训练样本全部训练完毕且满足网络精度要求或者达到了迭代次数，得到理想网络；

步骤5输入测试样本，输出检测结果。

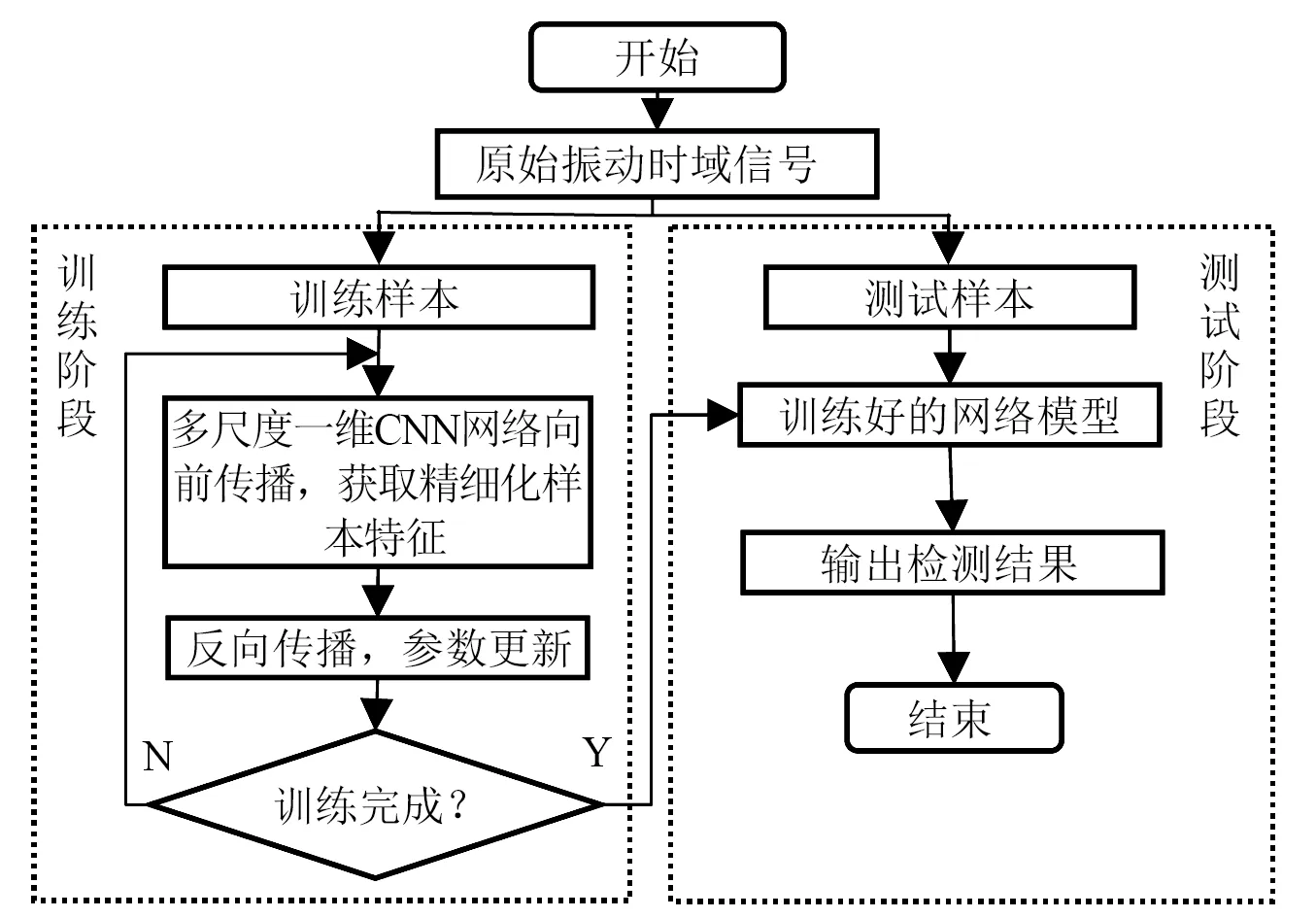
图3 方法流程图Fig.3 The flow chart of method

3 风机基础螺栓松动检测试验

通过风机基础连接螺栓松动情况进行检测试验。基础钢板上一共有10个连接螺栓，每个螺栓都存在预紧和松动两种状态。基础钢板上连接螺栓松动情况测试布置12个测点，12个通道采集。1～10号测点布置在1～10号螺栓旁边，测点11、测点12分别布置在两块安装支架上，安装及测试示意图如图4所示。

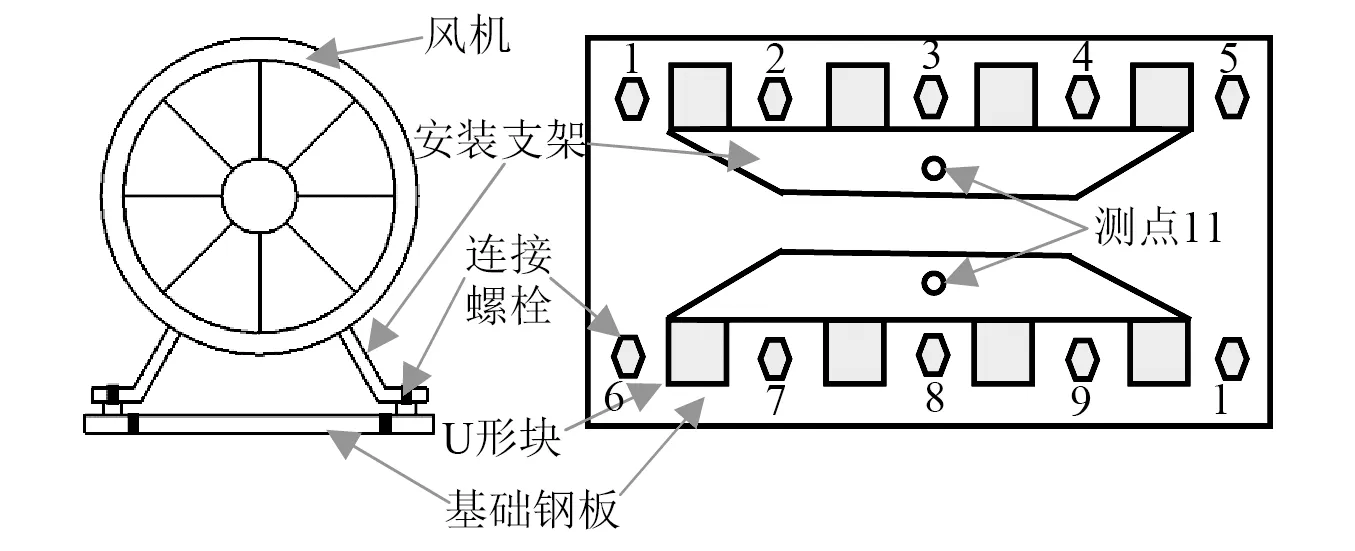
图4 安装及测试示意图Fig.4 Installation and test diagram

由于风机基础螺栓分布对称，试验模拟了5种典型的松动状态来采集其振动信号，如表1所示。其中：L1表示螺栓全紧；L2～L4表示不同数量螺栓松动程度。若松动程度达到L5以上(即松动螺栓数量超过4颗)，则风机运行非常危险，必须停机维修。试验采用PCB加速度传感器，NI9234采集卡；分别在风机稳定转速(1 500 r/min)和变转速(升速由500 r/min升至1 500 r/min,降速有1 500 r/min降至500 r/min)运行下采集振动信号，采样频率为25.6 kHz，采样长度为102 400点。

表1 风机基础连接螺栓松动程度Tab.1 Looseness of connecting bolts of fan foundation

3.1 网络参数设置

3.1.1输入样本构造

输入为一维振动时域信号，考虑深度卷积神经网络对样本数的需求，同时为充分利用试验数据，采用滑窗的形式截取训练和测试样本，如图5所示。滑窗长度为1 024，移动步长为512，可以使样本数量增加一倍，同时避免样本的截断导致特征丢失。

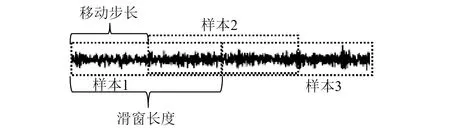
图5 滑窗构造样本示意图Fig.5 Schematic diagram of sliding window construction sample

3.1.2多尺度卷积层设置

多尺度卷积层设计主要包含卷积核尺度选取、卷积核个数n的确定两部分。根据样本长度，同时参照目前一维卷积神经网络对卷积核尺度的设置，卷积核尺度主要从1×2，1×5，1×10，1×20，1×32，1×64进行选取，以获取信号从低到高不同精细度的特征。针对两层多尺度卷积层设计思路如下：第一层多尺度卷积层设置尺度范围较大的卷积核，以提取范围更广的不同精细度特征；第二层使用尺度范围相对小的卷积核，对前面所提取不同精细度特征再次精细化，提取信号更高层抽象特征。同时针对两层多尺度卷积层中不同尺度卷积核个数n1，n2进行比选试验，根据上述设计思路，第一层多尺度卷积层卷积核个数n1=2时尺度分别为1×2，1×32，n1=3时尺度分别为1×2，1×32，1×64，n1=4时尺度分别为1×2，1×10，1×32，1×64；第二层多尺度卷积层卷积核个数n2=2时尺度分别为1×5，1×10，n2=3时尺度分别为1×5，1×10，1×20，n2=4时尺度分别为1×2，1×5，1×10，1×20。比选结果如表2所示。

表2 卷积核个数比选结果Tab.2 Comparison results of convolution kernels

由表2可以看出，在两层多尺度卷积层卷积核个数分别为3，3时，检测准确率达到99.7%，而再增加卷积核个数准确率差别不大，同时考虑网络尺寸和训练参数的增加使得网络模型占用计算资源和内存资源过高，导致训练速度降低。因而针对两层多尺度卷积层设置不同尺度卷积核个数均为3，第一层多尺度卷积层卷积核尺度分别为1×2，1×32，1×64，第二层多尺度卷积层卷积核尺度分别为1×5，1×10，1×20，两层多尺度卷积层设置步长分别为3，2。并设置padding方式为samepadding，避免边缘信息丢失，同时保证多尺度卷积层内并行的卷积层输出维度一致，以便特征拼接。

3.1.3 其余参数设置

池化方式设置为最大值池化，两层池化层池化核大小分别为1×2，1×4，步长均为2。全连接层单元数分别为500，100，针对全连接层设置Dropout和L2正则化以减少因多尺度卷积层设置带来的计算复杂度，同时防止过拟合。第一层Dropout设置在第一层全连接层前，系数为0.25，后两层Dropout分别设置在两层全连接层后，系数为0.5，L2正则化系数为0.000 1。选用交叉熵作为损失函数，衡量预测的Softmax输出概率分布和目标类概率分布的相似性。优化器选用AdadeltaOptimizer自适应调整学习率。批量大小为128，学习率为1.0，迭代次数为200。模型运行的软件环境为：python+keras。硬件环境为：Inter i7-8750H+Nvidia 1050ti。

3.2 稳定转速下基础螺栓松动检测

3.2.1 数据集划分

针对5种风机基础连接螺栓松动状态，每种状态选取样本数为190，共计950个样本。并以7∶3的比例随机划分训练集和测试集，其中训练集为665个样本，测试集为285个样本。训练集样本数目是确保网络是否训练充分以及模型检测精度的重要影响因素之一。一般来讲，网络层数和节点多则需要更多的训练样本，反之亦然。经多次试验，在此确定的训练样本数可满足所设置的网络训练之需求。

3.2.2 对比模型及参数设置

为评估所提方法的性能，将所提方法与二维CNN、使用单一尺度卷积核的一维CNN以及韩坤林研究中人工提取特征算法进行对比。单尺度一维CNN在卷积层设置单一尺度卷积核，两层卷积层卷积核尺度分别为10，5，其余参数与所提方法设置一致。二维CNN参照经典卷积神经网络Lenet5结构，结合Wen等的研究将时域信号转化为二维图像的方法，构造32×32大小的二维图像作为输入。各CNN算法学习率、批量大小、迭代次数、损失函数及优化器设置均相同。人工提取特征算法参照韩坤林的研究构建包含11个时域特征参数和13个频域特征参数的24维混合域特征集，以LLTSA流行学习算法降维后输入KNNC获得检测结果。

3.2.3 试验结果及分析

为展现所提方法相对于单尺度一维CNN和二维CNN的优势。每个CNN经过200次迭代，每次迭代更新权重后输入测试集进行测试，得到风机稳定转速下不同方法准确率对比曲线,如图6所示(曲线通过smooth函数拟合),同时计算单次迭代时间，如表3所示。

图6 稳定转速下不同方法准确率对比Fig.6 Comparison of the accuracy of different methods under steady speed

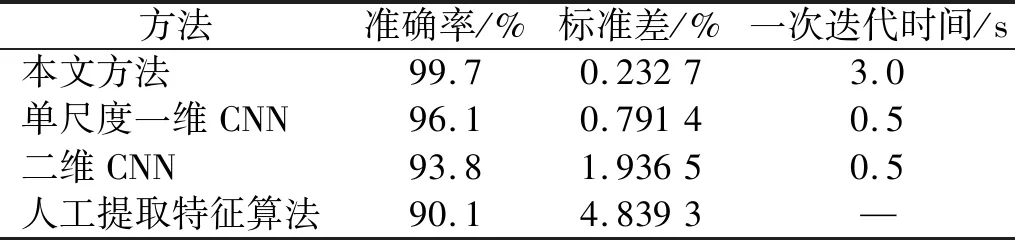
表3 不同方法检测结果Tab.3 Test results of different methods

由表3各CNN方法一次迭代时间对比可知，本文方法一次迭代时间相对于另外两种CNN方法稍长，其主要原因是本文方法是一种多尺度并行处理算法模型，其空间复杂度稍高导致耗时有所增加，而对于训练完成的各CNN方法，输入测试样本进行测试，时间以毫秒计，差异可忽略。由图6可以看出，随着迭代次数的增加，各组的准确率不断提高。对比一维CNN模型和二维CNN模型，一维的CNN模型在检测准确率上均优于二维的网络模型，证明了一维的CNN模型更适合于时域信号的处理；同时，所提方法在检测准确率上均优于其余两种方法，在迭代50次时便达到99%以上检测准确率，且随迭代次数增加，检测精度波动平稳；单尺度一维CNN迭代50次时准确率为80.15%，在迭代100次后趋于平稳；二维CNN迭代50次时仅达到32.12%，在迭代150次后趋于平稳。展现了所提方法在风机稳定转速下能有效地对风机基础螺栓松动进行检测，且所需迭代次数更少，弥补了本文方法单次迭代时间稍长的缺陷，稳定性好。

所提方法随机抽取样本后10次训练和测试后取平均，得到平均准确率，并计算其标准差，同时与人工提取特征算法检测结果作对比，检测结果如表3所示。从检测结果可以看出，相对于人工提取特征算法，卷积神经网络算法平均准确率均高于人工提取特征算法，证明了卷积神经网络自适应提取信号深层特征更具备优势。所提方法平均检测准确率达99.7%，优于其余算法，且标准差更小，证明了所提方法能对风机基础螺栓松动有效检测，方法是可行、有效的，且偏差小，稳定性好。

3.2.4 特征学习验证

为展现所提方法精细化提取特征的优势，利用t分布随机邻域嵌入(t-distributed stochastic neighbor embedding,t-SNE)对上述各卷积神经网络模型倒数第二层全连接层学习到的特征进行分析和可视化，并将韩坤林研究中人工提取特征算法进行对比，如图7所示。由图7可知，对于人工提取特征算法，所提取到的特征存在多个部分混叠在一起，特征分离度不高，无法对风机基础螺栓松动状态进行有效表征；对比各组CNN算法特征可视化结果，所提方法所提取的同一种松动状态特征很好地聚集在一起，不同松动状态的特征则被有效地分离，而其余两种CNN算法提取的特征均存在部分混叠，证明了本文方法精细化提取特征更具备优势，所提特征具有良好的分类性能，能有效表征风机基础螺栓松动状态。

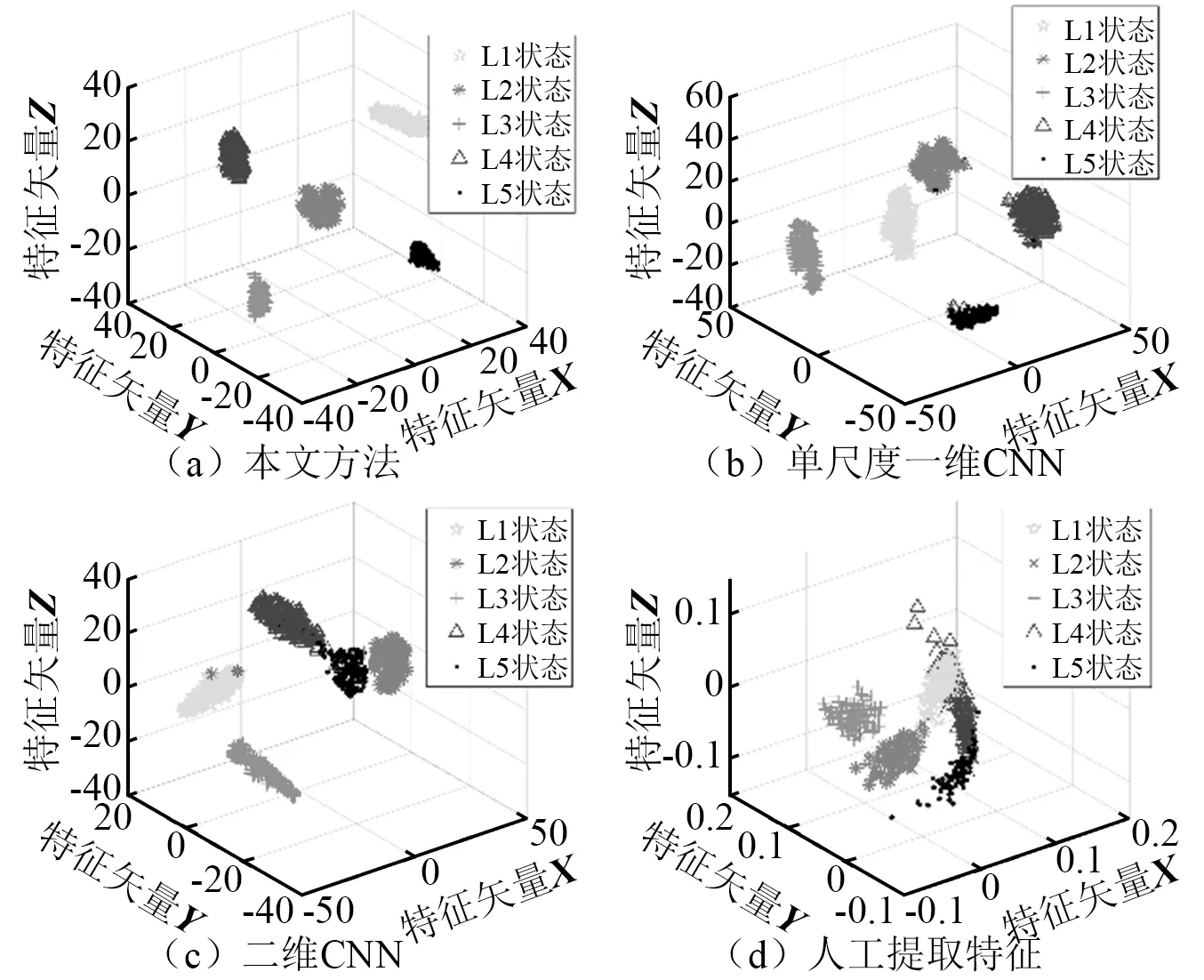
图7 学习特征t-SNE分析Fig.7 t-SNE analysis of learning features

3.3 变转速下基础螺栓松动检测

工程实际中，不同风机通常具有不同的运行转速，采集的振动信号因受转速影响存在差异。所提方法以其多尺度精细化提取信号深层特征的特点为适应不同转速下风机基础螺栓松动智能检测提供了可能。通过风机升速和降速运行时采集振动信号，涵盖从500～1 500 r/min的转速情况以适应对不同转速风机的智能检测。针对5种风机基础连接螺栓松动状态，每种状态取样本数为380(包含风机升速、降速两种变转速状态各190个样本)，共计1 900个样本，同样以7∶3的比例随机划分训练集和测试集，其中，训练集为1 330个样本，测试集为570个样本。对比人工提取特征算法、二维CNN、单尺度一维CNN三种算法。

3.3.1 试验结果及分析

经过200次迭代，风机变转速下不同CNN方法准确率曲线如图8所示，不同方法检测结果如表4所示。由图8可以看出，风机变转速下，所提方法在检测准确率上仍优于二维CNN方法和单尺度一维CNN方法，在迭代50次时准确率达到97.19%，单尺度一维CNN为77.02%，二维CNN仅56.32%。由表3可知，变转速下，人工提取特征算法检测准确率仅为75.6%，单尺度一维CNN为93.8%，二维CNN为85.8%，所提方法仍保持98.9%的高检测准确率，且标准差小，证明了所提方法在变转速下也具备良好的检测能力，可适应不同转速下风机基础螺栓松动检测。

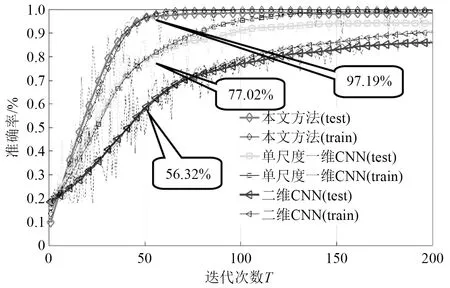
图8 变转速下不同方法准确率对比Fig.8 Comparison of the accuracy of different methods under variable speed

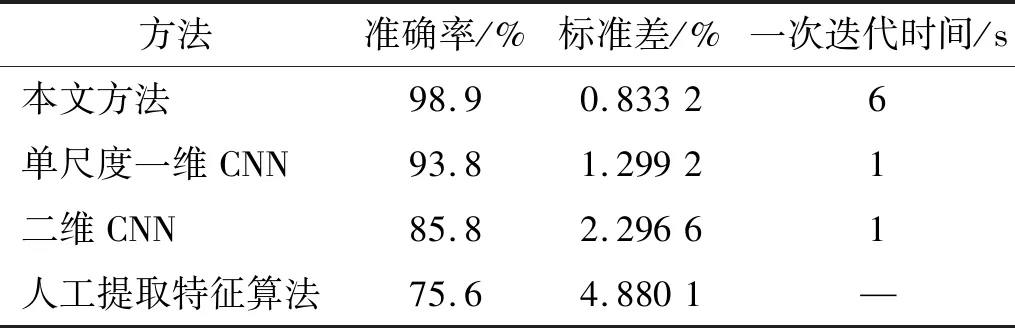
表4 变转速下不同方法检测结果Tab.4 Test results of different methods under variable speed

3.3.2 特征学习验证

为验证变转速下所提方法特征提取能力的优势，同样利用t-SNE对各算法所提取特征进行分析和可视化，如图9所示。根据图9，所提方法在风机变转速下所提取到的各松动状态特征同样具备较高的分离度，其余三种算法各松动状态特征混叠明显，证明了所提方法精细化特征提取的优势，具备更好的特征学习能力，能从风机变转速下的原始时域信号提取到有效的特征。

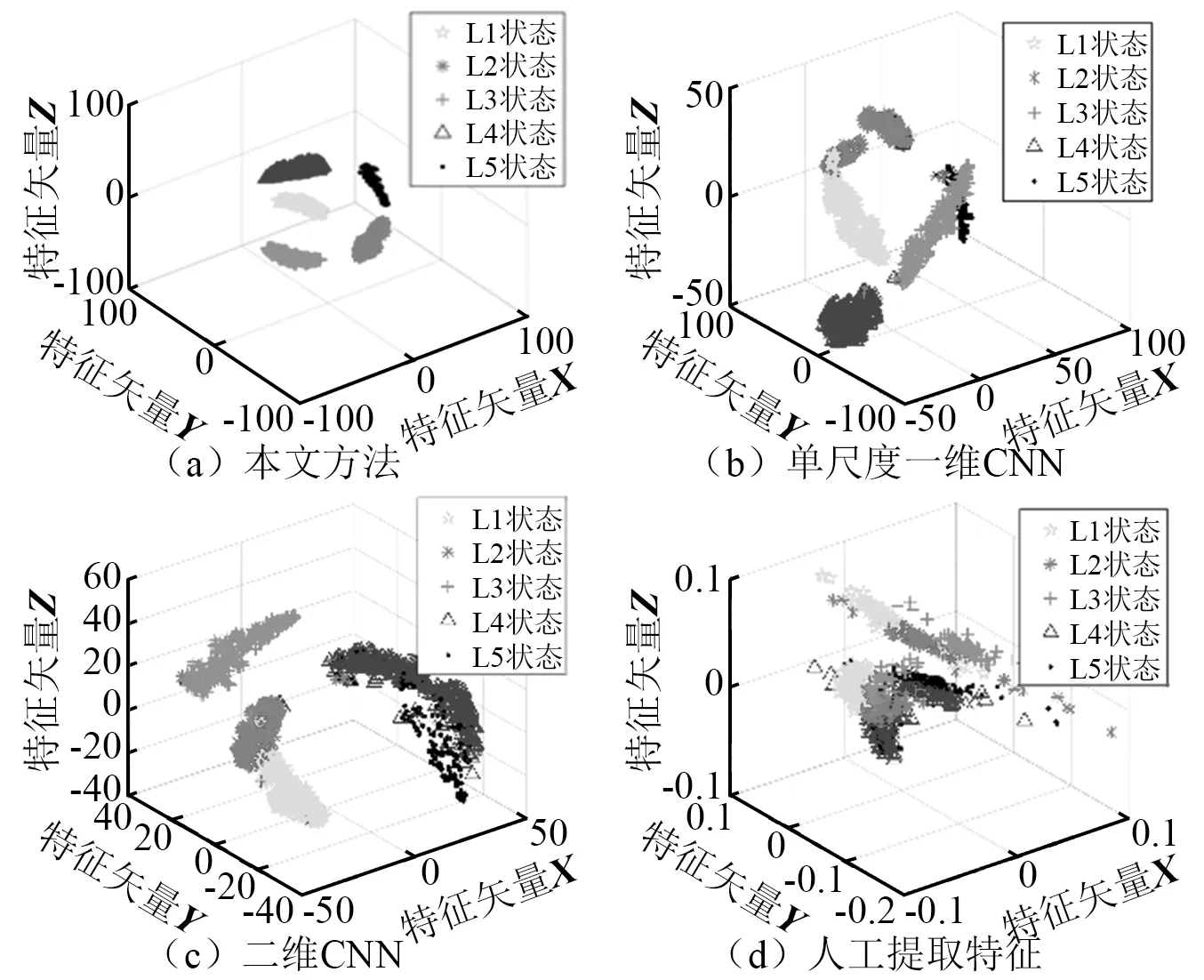
图9 学习特征t-SNE分析Fig.9 t-SNE analysis of learning features

4 结 论

多尺度一维卷积神经网络的风机基础螺栓松动智能检测方法将原始振动时域信号作为输入，通过多尺度卷积运算将风机基础螺栓松动状态特征精细化表征，并与模式识别有机融合在一起，整个过程摆脱了对信号处理和专业知识的依赖，让模型从原始信号自动学习信号特征完成松动检测，解决了风机基础结构振动信号(特别针对存在转速变化情况)特征提取难的问题，实现了“端到端”的风机基础螺栓松动智能检测。所提方法的主要优势在于：运用一维的网络结构来处理一维时域信号，减少了信号预处理的工作量，更利于对悬挂风机基础螺栓松动实时智能检测；运用多尺度卷积运算，融合不同尺度提取的特征信息，使不同尺度特征之间信息相互补充，以对原始信号特征精细化表征；通过在稳定转速和变转速运行下对悬挂风机基础螺栓松动检测试验，证明了所提方法能有效地对风机基础螺栓松动进行检测，且可适应不同运行转速风机，并具有良好的稳定性。

下一步研究重点算法的计算效率提升，以及螺栓由预警到松动的中间状态的检测和不同型号风机间的螺栓松动检测方法。