基于相对密度核估计的实时剩余寿命预测
2022-12-01张江民董增寿
张江民,石 慧,董增寿
(太原科技大学 电子信息工程学院,太原 030024)
近年来,随着工业化设备不断地朝着智能化、高性能和复杂化的方向发展。这类设备在受到系统内部因素和外部环境因素的影响下设备发生故障的概率也随之增加,设备故障会导致其性能和健康状态产生一定程度的退化。如果设备出现大的故障,这不仅造成财政和资源损失重大,也给人民的安全带来危险[1-2]。为此,对设备进行实时监测和剩余寿命预测有着十分重要的研究价值和意义。现研究阶段可将剩余寿命预测的方法大致分为基于物理失效模型、基于知识表示和数据驱动的方法[3]。面对复杂化的设备,获得物理模型是非常困难的事,知识表示的方法更适合于定性推理而不太适合定量计算,且难以获得完整的知识。因此,数据驱动的方法成为剩余寿命预测研究的主流方向[4]。
Si等[5]将数据驱动方法的伽马分布、回归模型、维纳过程和随机滤波模型等[6]寿命预测方法进行总结分析。Zhai等[7]提出自适应维纳过程的剩余寿命预测模型。刘文溢等[8]提出基于高阶隐半马尔科夫模型的剩余寿命预测模型。上述数据驱动方法大部分需要假设退化模型和参数估计,并且参数估计法对模型选择有局限性,过分依赖概率密度函数形式的先验界定,所以不能确保预测模型的精确性和适用性。随着工业系统复杂化的发展,机器学习作为数据驱动的方法,裴洪等对基于机器学习的预测方法从浅层和深度学习两方面进行了详细分析总结。其中,基于深度学习的预测方法有强大的特征提取能力,不需要事先对未知的退化模型假设,是目前剩余寿命预测应用上的主流方法。Zhang等[9]提出用LSTM神经网络的方法对设备进行预测。Li等[10]利用深度卷积神经网络方法进行寿命预测。而Chen等[11]结合了Guo等[12]和Li等两种方法的优势提出了一种基于端到端可训练卷积递归神经网络的机械健康指标构建方法。张继冬等[13]提出一种基于全卷积变分自编码网络的轴承剩余寿命预测方法。上述机器学习的方法,它的算法在适应制造系统和过程的复杂和非线性特性方面往往受到限制,而且其模型内部结构称为‘黑盒子’,不能够清楚地表征系统退化特征的变化,且网络在学习过程中随着输入的不断增加,参数调节不能保证全局最优,从而使系统的剩余寿命预测准确性受到影响。
核密度估计的方法是对数据分布不附加任何假设,从数据本身出发研究数据分布特点的非参数估计方法[14]。该方法避免了大部分数据驱动方法需要模型假设和参数估计的问题以及避免了机器学习的不足。因此,核密度估计方法在剩余寿命预测技术上的应用受到学者们的高度关注和重视。现有的核密度估计模型中,Hu等[15]用非参数核估计的方法对风速建模评估系统可靠性。Sidibé等[16]针对不同运行环境对随机系统退化状态的作用,提出用两个函数建模的方法对系统可靠性进行了计算。杨楠等[17]提出一种基于非参数核密度估计的风功率波动性概率密度建模方法,并针对模型带宽选择问题,构造一种以拟合优度检验为约束条件的带约束带宽优化模型。李存华等[18]将核密度估计方法应用在聚类算法的构造上,提出基于网格数据重心的分箱核估计近似方法。上述文献中核估计窗宽的选取大部分采用的是固定的窗口宽度,将固定值作为窗宽会造成样本点分散的区域拟合度低,密集的区域拟合度过高。为了解决固定窗宽的不足,赵渊等[19]提出一种非参数多变量核密度估计负荷模型研究的方法,该方法在核估计窗宽选择上实现了自适应选取窗宽。颜伟等[20]针对核估计中最优带宽选取的重要性,提出一种不依赖总体真实分布的最优带宽改进模型。为了提高预测的准确性,张卫贞等提出的实时剩余寿命预测方法,将积分均方误差方法引入核估计窗宽的选择上实现了自适应窗宽选取。上述方法能够自适应的选择窗宽和实现了特征退化分布和剩余寿命预测的实时更新,但是在数据分布不均匀的、变密度的样本处选择窗宽的合理性有待提高。而且现有核密度估计模型在有界支持[0,+∞]上的核估计量在0附近是有偏的,并且从支持的原点引入了一个值为-h的左移。会使得剩余寿命估计的准确度降低,Silverman[21]提出对有界支持[0,+∞]的对数变换;这样就可以处理无界支持[-∞,+∞];这种转换减少了零附近的初始偏差。在Silverman的基础上Saoudi等[22]提出微分同胚变换的方法,该方法除了在边界附近是弱偏差外,且还满足核密度估计的统计性质,即一致性、渐近正态性和非偏性。Sidibé等针对不同环境下维修优化问题,提出了核微分同胚可靠性函数估计方法,并与J-Sh变换法[23]进行比较,结果表明核微分同胚估计具有更好的收敛性,能够更好的解决边界偏移问题。
鉴于此,本文提出了一种相对密度核估计的实时剩余寿命预测方法。首先,建立非参数核密度估计剩余寿命预测模型,利用k近邻距离计算样本点的相对密度来构造自适应相对密度窗宽模型,以能够对任意形状,密度不均匀的数据集进行有效分析,并根据样本数据的密度自适应地选择窗宽值进行自适应核密度估计,即高密度区域采用较小的核窗宽,而低密度区域采用较大的核窗宽,以提高核密度估计的准确性。其次,在剩余寿命预测模型的构建上,引入微分同胚映射的方法来解决预测在边界的偏差性和无界性,该方法利用微分同胚变换将有界随机变量变换到整个实数域,从而转换为传统意义上的核密度估计问题进行求解,从而提高预测的平滑性和准确性。通过相对密度核估计的剩余寿命预测模型实时更新的递推算法,以避免每增加一个样本数据就要进行一次计算带来计算量复杂问题。最后,采用齿轮磨损试验和滚动轴承的加速寿命试验来验证本文模型的有效性和准确性。
1 核密度估计模型
核密度估计方法对数据分布不附加任何假定,是一种从数据本身出发,用来估计未知变量的概率密度函数的方法。其由已知的N个样本点,通过选择任意核函数(如高斯核函数)及窗宽得到N个核函数,再线性叠加形成核密度的估计函数。例如,对样本集为
在现有的研究中,自适应窗宽的窗宽选择法已经成为一个发展趋势,该方法能够在监测数据实时变化的情况下,自适应的选择合理的窗宽,也能解决固定窗宽带来数据拟合不足和过度的问题。而通过k近邻思想[24]计算样本点的相对密度,其能通过样本点之间的k近邻距离范围判断出各样本点与其周围样本点的稀疏和密集程度,从而选择合理的相对密度。此外,相对密度的思想本质就是直接对数据分析计算来判断密度的大小,与核密度估计思想不谋而合,而且能够对任意形状的数据集进行快速、准确地识别样本的中心。因此可以将k近邻思想计算样本点的相对密度引入自适应窗宽来提高核密度估计的准确性。
中国乳制品进口价格的由乳制品的进口数量和乳制品的进口金额获得。其选取的样本区间为2006—2016年,记作ln P。
x={x1=-2.1,x2=-1.3,x3=-0.4,x4=1.9,x5=5.1,x6=6.2}的核密度估计拟合结果如图1所示。
深谙选择重要的刘备,对关、张的行为提出批评。说“孤之有孔明,犹鱼之有水也。愿诸君勿复言”。看看,刘备的着眼点,是为合作者,打造能够干事的平台。后来的实践,更证明诸葛亮选择的重要。反过来,平台步步惊心、处处障碍,正确的得不到弘扬,错误的却左右大局,结果只有一个,逼着合作者“重新选择”。

图1 核密度估计示意图Fig.1 Schematic diagram of kernel density estimation
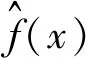
(1)
式中:h为窗宽;K(·)为核函数;n为样本数。其中,核密度估计取决于K(·)和h的选择。
核函数作为影响核密度估计的一个因素,一般情况下任何函数都可作为核函数,常用的有四次核、均匀核、三角核和高斯核。核函数的选择对核密度估计的准确度作用不大。本文选用广泛应用的高斯核函数。
(2)
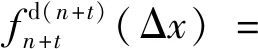
(1)固定窗宽是在核密度估计时采用固定不变的值。这种选取窗宽的方法一般会导致核估计在低密度区拟合不足,高密度区过度拟合。通过图2可以清楚的分析出固定窗宽的不足之处。
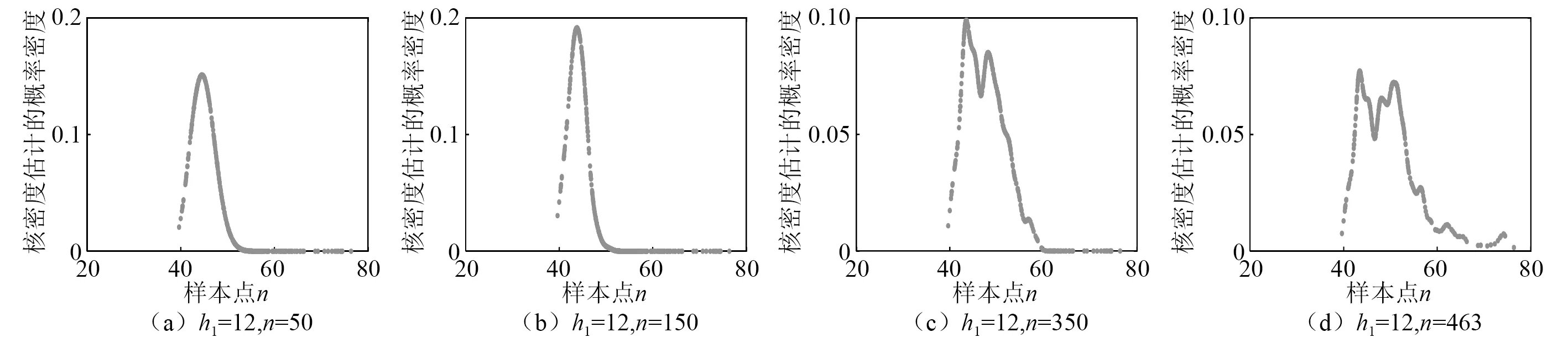
图2 固定窗宽下的核密度估计示意图Fig.2 Kernel density estimation with fixed window width
图2为固定窗宽h1=12,在四组样本数据密度不同情况下的核密度估计示意图,由图可知在数据不足的区间,核估计欠拟合;在数据集中的区域,核估计过度拟合。
(2)目前自适应窗宽是窗宽选择的主流方向,其本质是随着样本点的增加能够自适应的选取窗宽,提高估计准确度。在现有研究阶段常用的自适应窗宽方法大多采用的是通过式(3)积分均方误差求其最小值得到初始最优窗宽hn。
(3)
通过以上递推可知,当任意tn+j时刻增加j个样本时,n+j个样本数据的核密度估计可递推为
(4)
将高斯核函数代入式(4)可求出hn为
(5)
式中,σn为n个初始样本特征退化增量的方差。
1.2.1 细胞培养及转染 SHG-44细胞用含10%胎牛血清的RPMI-1640培养基于37℃、5%CO2的培养箱内培养,根据Lipofectamine2000操作说明转染miR-543 mimic及mimic NC序列、miR-543 inhibitor及inhibitor NC序列。实验分为5组:Con-trol(对照组)、mimic NC组、inhibitor NC组、miR-543 mimic组和 miR-543 inhibitor组。细胞转染48 h后,进行后续实验。
上述自适应窗宽方法在实际应用中,解决了样本数据在实时变化下选取窗宽以及固定窗宽造成过(欠)拟合问题。如果样本接近于正态分布时,选取该方式是最优选择。但是当真实分布为非对称或者多峰时,该方法可能导致过度平滑,准确性有待提高。
2 相对密度窗宽的确定
其四,“此在单元”的微观视域是推动中国城市社会发展的落脚点。“此在单元”是不同的家庭、社区、日常生活的实在场域,是人们的共性与个性基本关联单位,城市命运共同体合理性构建是宏观性政策与各项制度实现的合法性路径与社会发展的稳定基础。“此在单元”之间的差异性及其共融性,是宏观环境正义化与公平化在实践中使人们获取幸福感和满足感,以及实现人的自由全面发展的价值所在。因此,鼓励民间社会组织的发展,细心经营家庭与社区的紧密性,给城市社会不断注入活力且形成城市行动与行为合力,是克服奥尔森所指出的“集体行动悖论”的有效方式。
从世界范围看,城市基础设施项目投资的特点是投资量大、回收时间长,只有通过收费、享受政策优惠或得到政府补贴才能弥补经营亏损。引进社会资本是解决政府一次性投入不足的办法,但前提一是要有完善的基础设施投资、建设、运营的市场化环境,二是创新融资方式和金融工具使社会资本大规模进入。资本的本性决定了只有能产生收益的项目才能成为其追逐的对象,政府在一定范围内通过价格调整减少乃至消除投资带来的亏损,是投资建设必要的前提。因此,垃圾处理的市场化基础是建立收费制度,同时政府有足够的经济能力。德国是世界上实施垃圾收费制度最有效的国家之一,垃圾处理价格机制非常完善,使垃圾处理设施的建设投资和运营费用有了可靠保证。
2.1 相对密度的模型建立
假设x1,x2,…,xi,…,xn为n个样本点并用数据集A表示,则相对密度的模型建立过程如下:
步骤1计算样本点xi与样本点xj的欧式距离
(6)
步骤2计算样本点xi的k近邻距离[25]
k_dist(xi)=d(xi,xj),并且满足:
a) 对于任意正整数k,在样本中至少有不包括xi在内的k个点x′j∈A{xi},则d(xi,x′j)≤d(xi,xj);
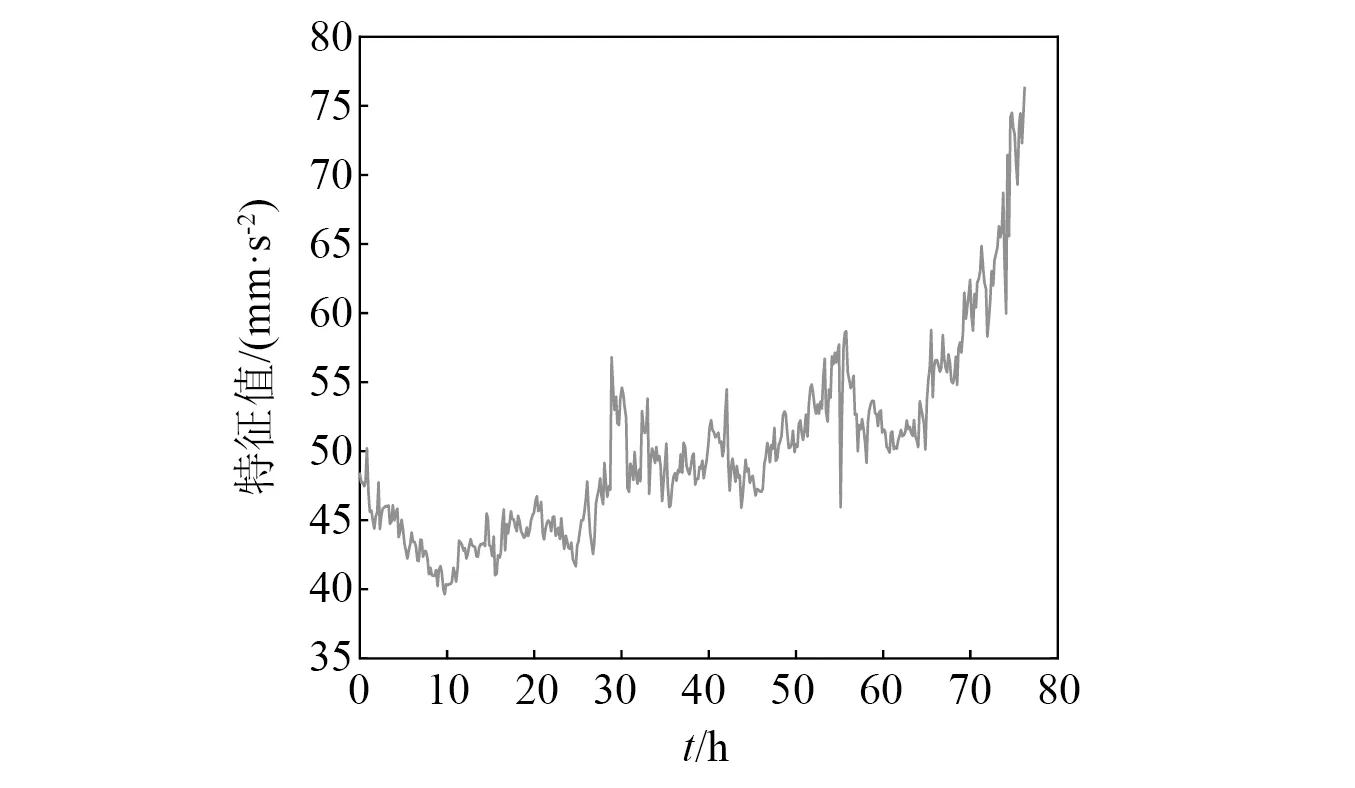
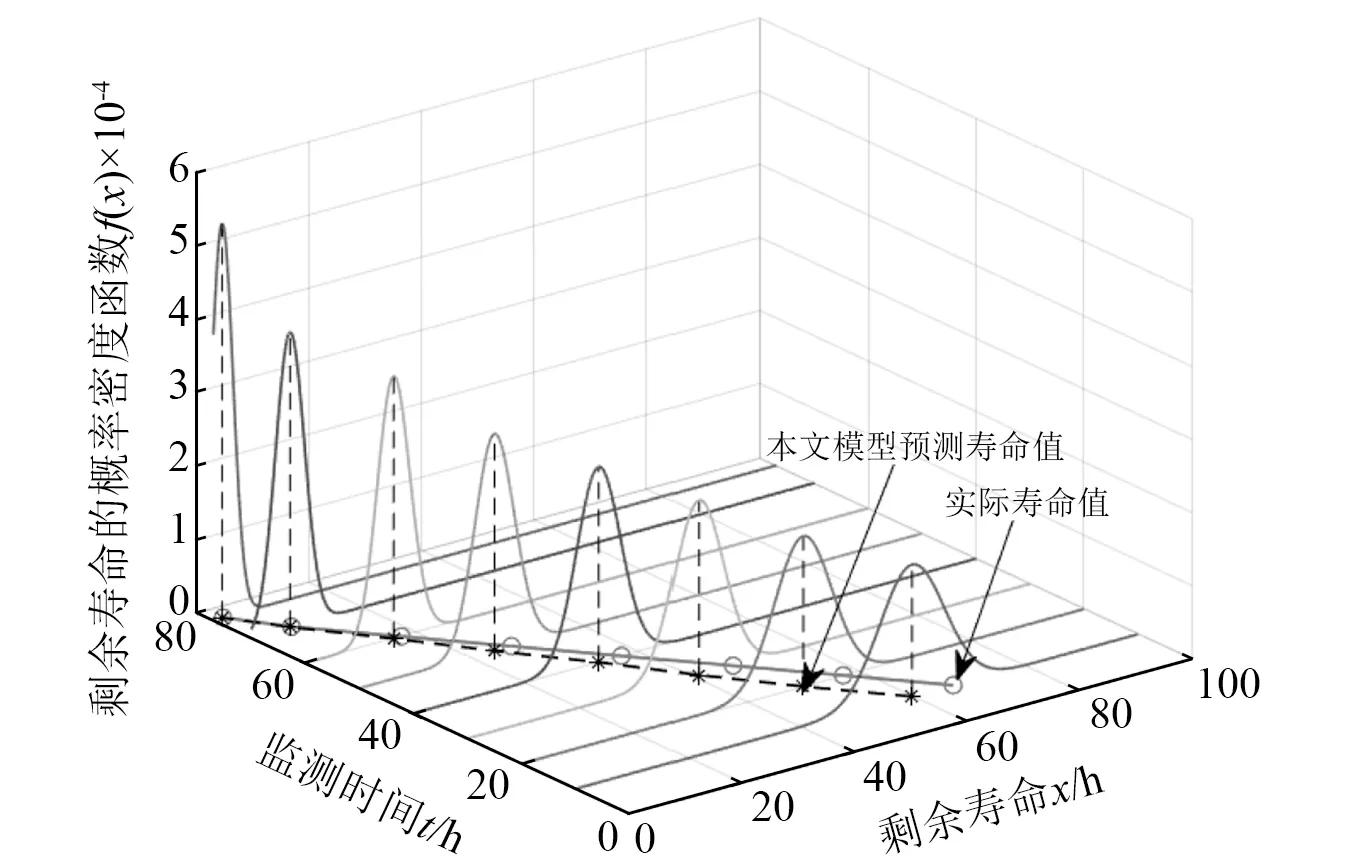
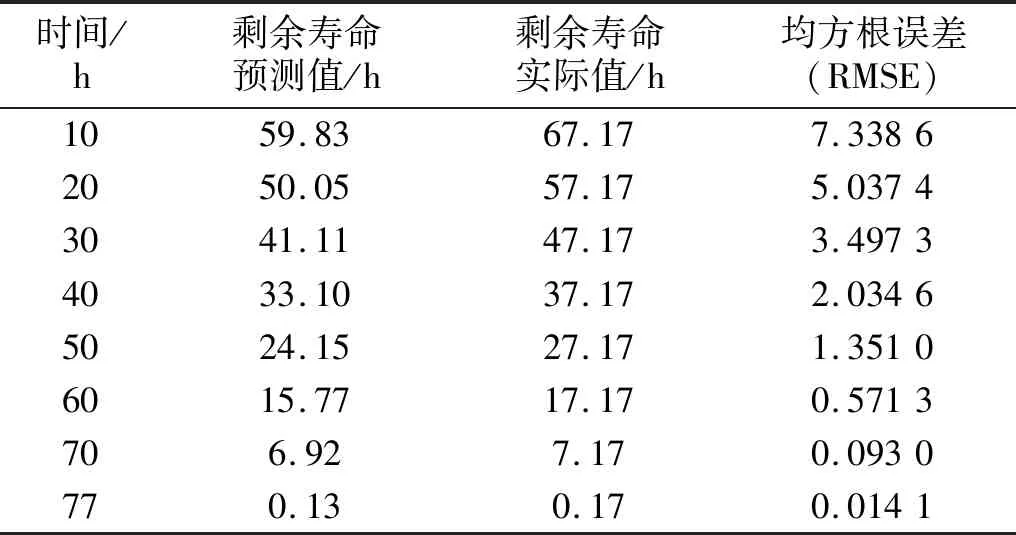
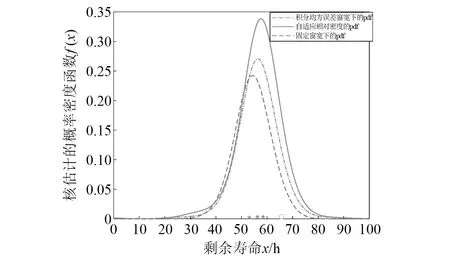
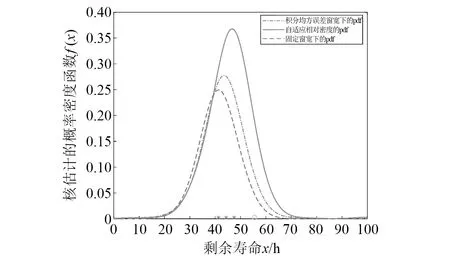
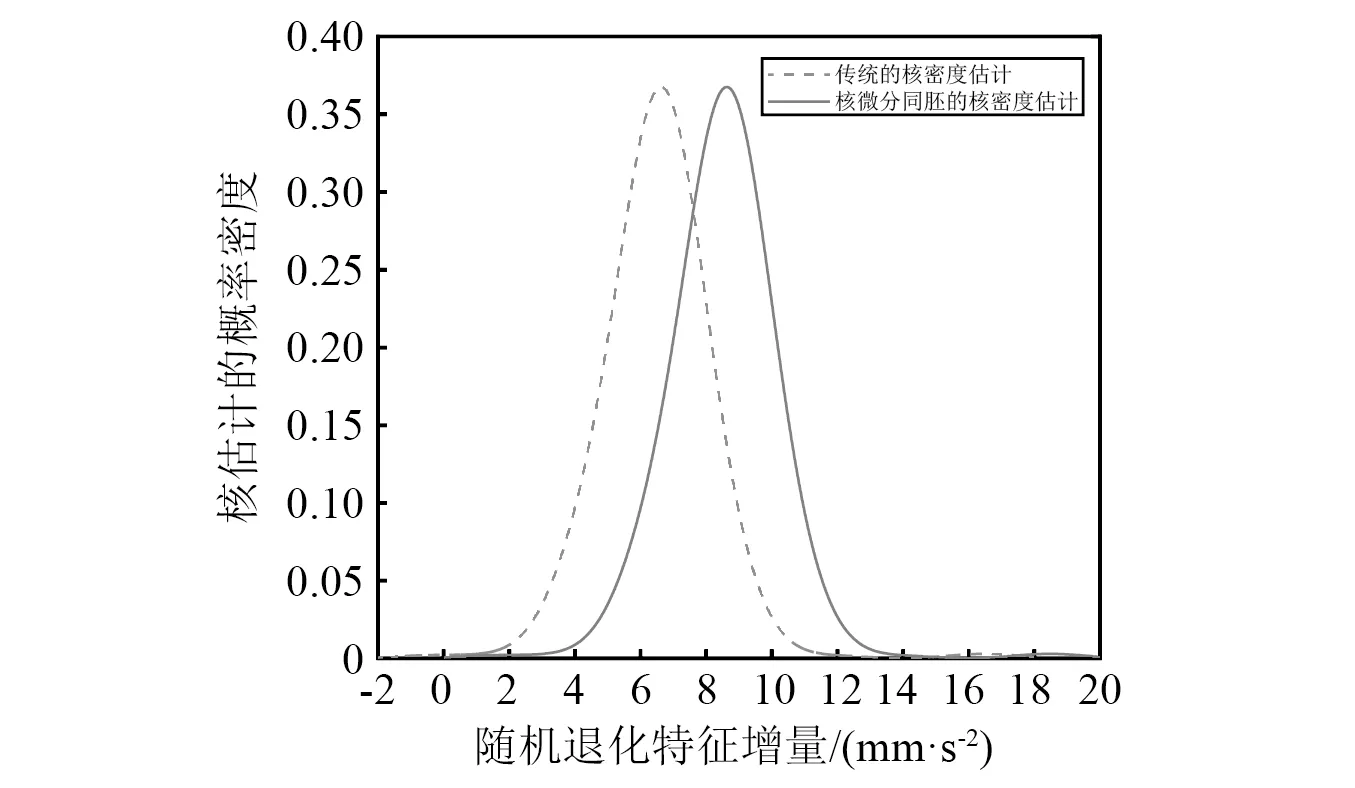
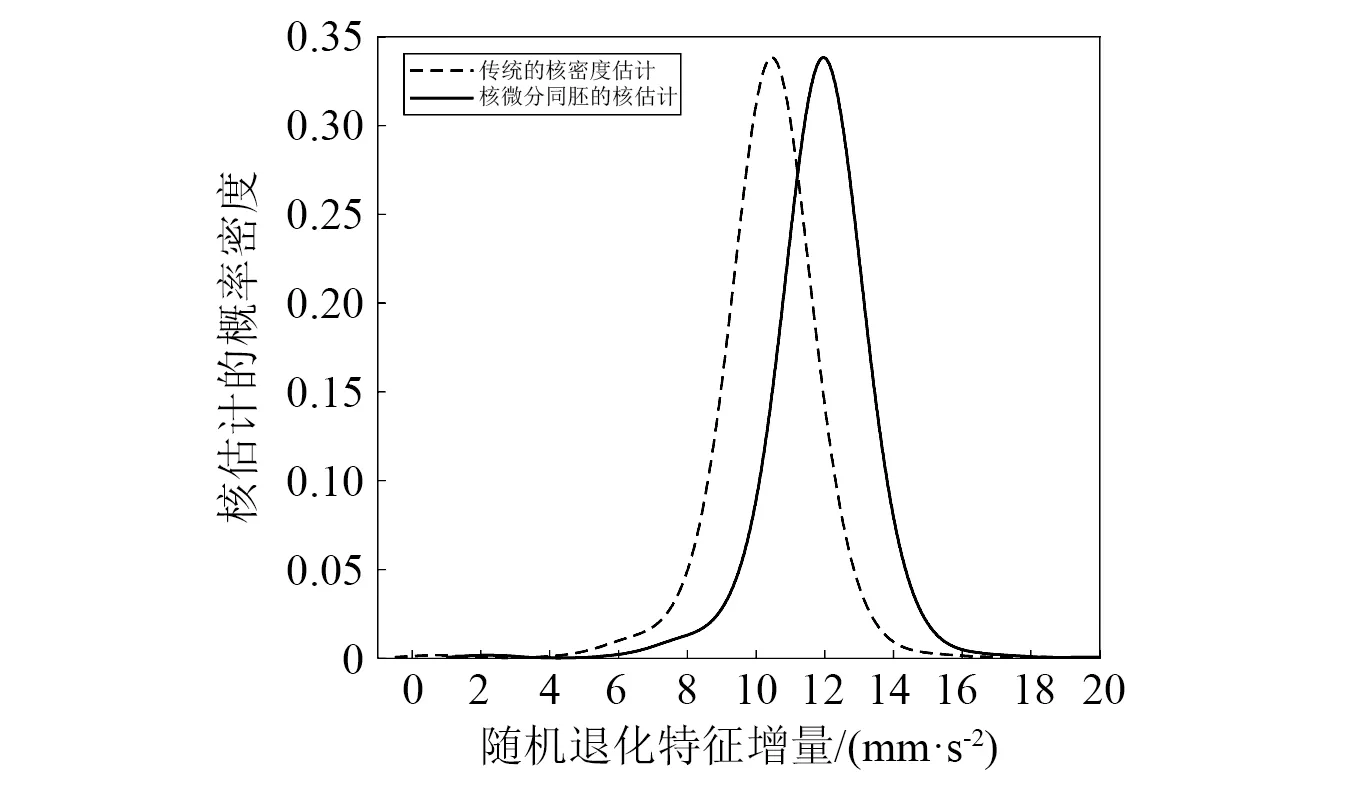
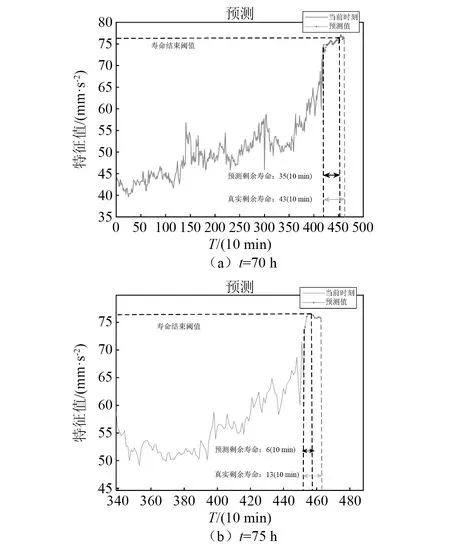
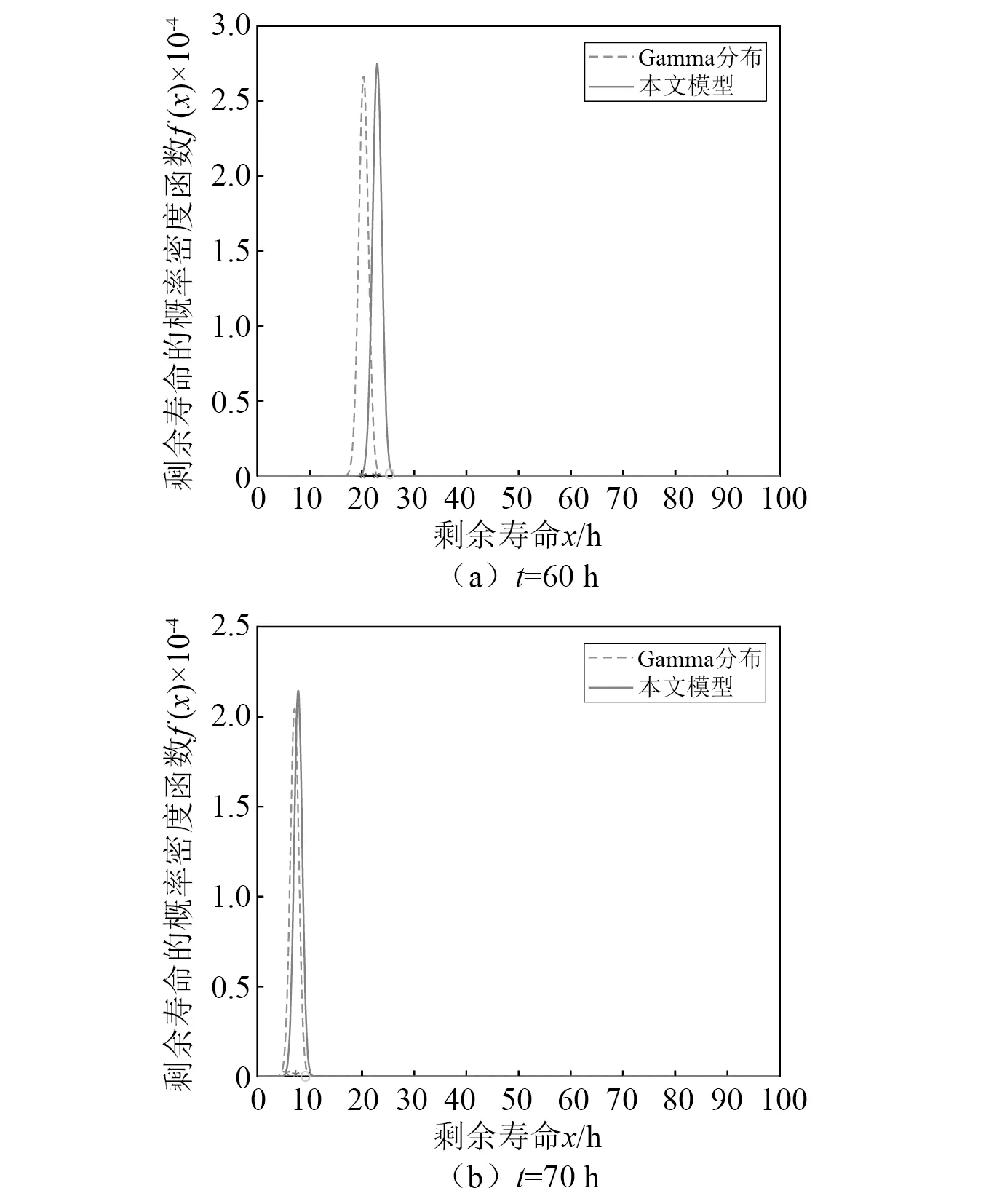
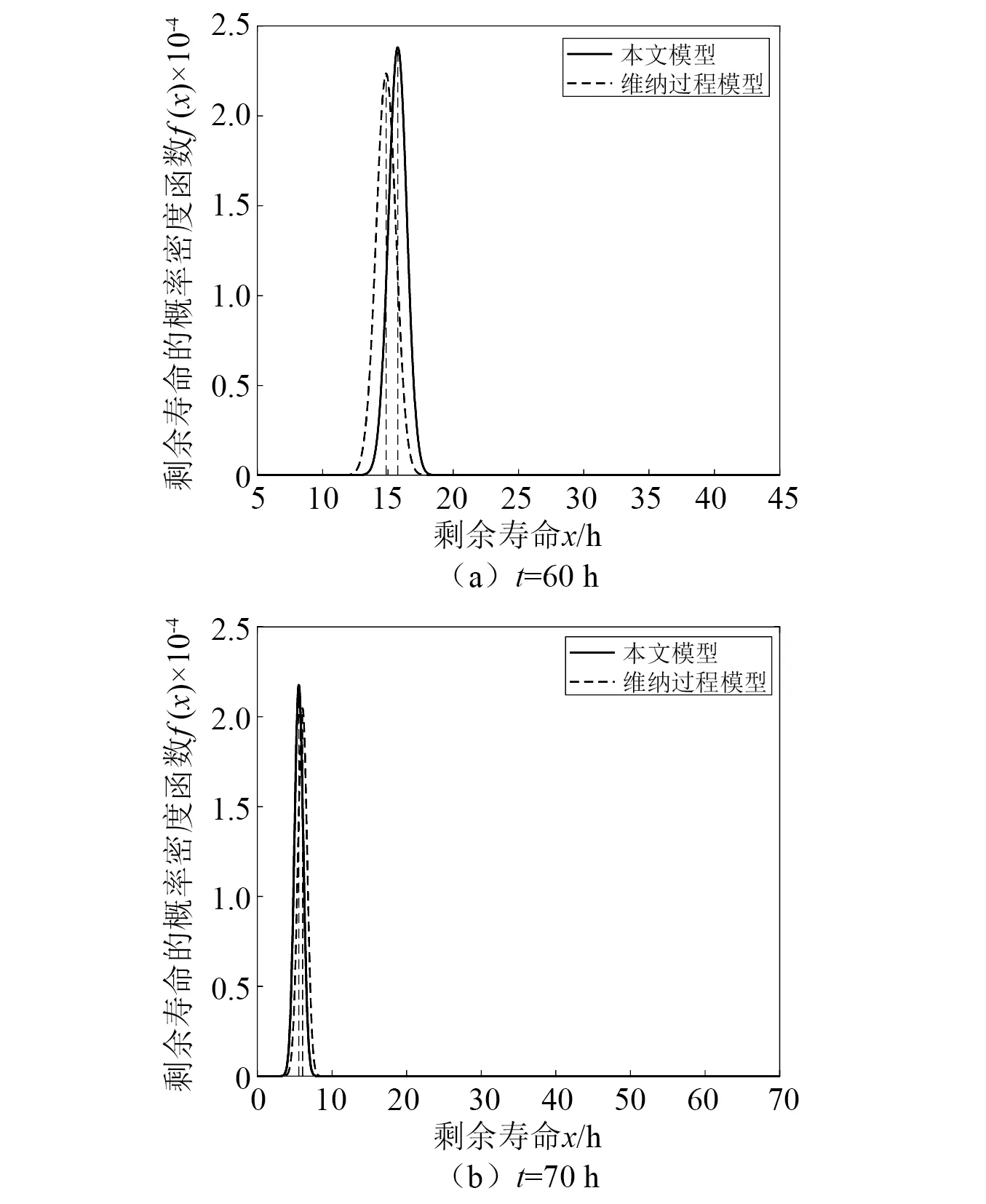
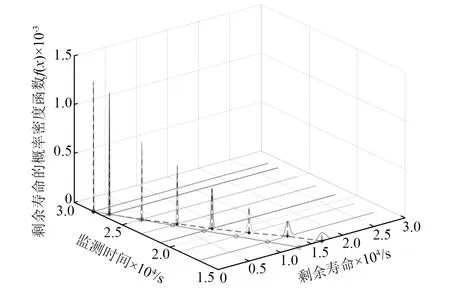
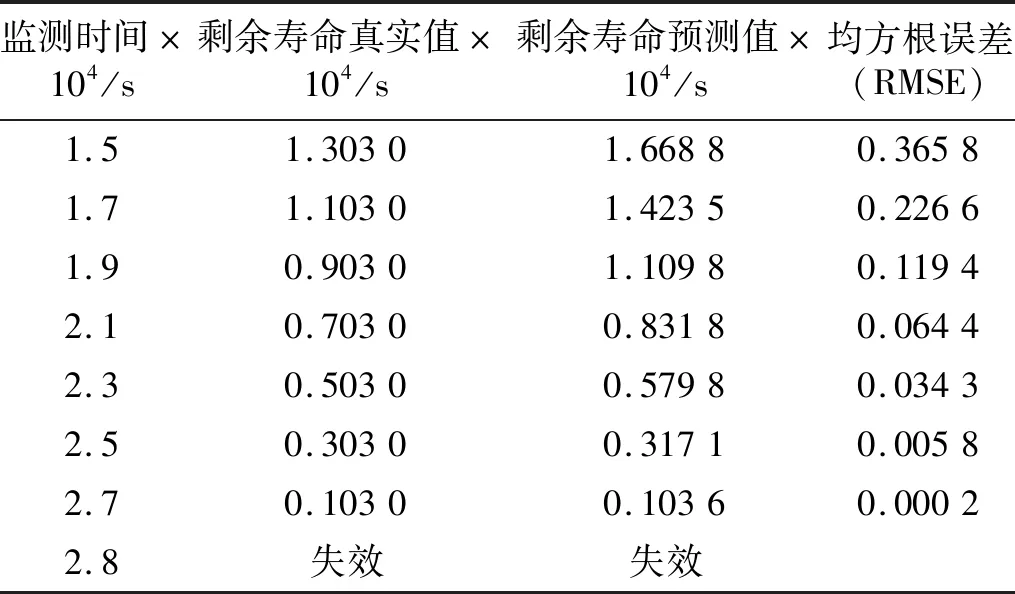
b) 样本中最多有不包括xi在内的k-1个点x′j∈A{xi},满足d(xi,x′j) 式中,k_dist(xi)为样本点xi的k近邻距离。 步骤3已知k_dist(xi),样本点xi的k距离邻域可表示为 (7) 式中:Nk(xi)为样本点xi的k距离邻域包含到xi的距离不大于k_dist(xi)的所有样本;x′i为xi的k近邻;d(xi,x′i)为xi和x′i的欧式距离。 步骤4计算样本点xi相对于xj的可达距离 为消除核估计的边界偏移,使其准确性提高,对有界系统退化增量进行对数核微分同胚变换[26] 比如,跑腿小哥,他们每天“往死里跑单”,跑得多的每天至少有两三百千米,但是却没有社会保障。甚至在具体协议中,由于不存在劳动关系,劳动者与平台之间不存在缴纳相关社会保险的义务,而劳动者由于患病或工作期间负伤,应自行承担相关责任,与平台方无涉。可见,零工经济带来了自由和效率,但也让劳动关系确认变得更加复杂。 (8) 式中:reach_dist(xi,xj)为样本点xi相对于xj的可达距离;d(xi,xj)为样本点xi与xj之间的欧氏距离,k_dist(xj)为样本点xj的k近邻距离。 步骤5计算样本点xi的局部可达密度,可表示为 (9) 式中:lrd(xi)为样本点xi的k距离邻域内点到xi的平均可达距离的倒数;|Nk(xi)|为样本点xi的k距离邻域内所有样本。 步骤6样本点xi的相对密度ρ(xi)可表示为 (10) 式中:样本点xj为k距离邻域内所有样本点;lrd(xj)为样本点xj的局部可达密度。通过上述推导将式(9)代入式(10)可推出相对密度ρ(xi)的表达式为 处于妊娠期,尤其是对于孕晚期的产妇来说,其往往会处于一种致糖尿病状态,极容易导致妊娠期糖尿病的发生[1]。若产妇的机体无法自主增加分泌胰岛素,来克服妊娠期出现的胰岛素缺乏情况,则会导致妊娠糖尿病发生。而随着妊娠糖尿病发病情况增加,临床咋检验技术方面也在不断进步,其中糖化血红蛋白检测在临床中应用最为广泛[2]。该次研究了2016年1月—2017年12月收治的60例妊娠糖尿病患者与60名健康妊娠产妇,分析了妊娠糖尿病筛查中即时检验糖化血红蛋白的应用价值,具体报道如下。 (11) 从公式不难看出相对密度ρ(xi)表示的是样本点xi的局部可达密度与样本点xi的k距离邻域内的样本点|Nk(xi)|的局部可达密度平均值之比。如果ρ(xi)越接近1,则点xi的邻域点密度相对均匀;若ρ(xi)越小于1,则点xi的密度高于其邻域点密度,xi为密集点;ρ(xi)越大于1,则点xi的密度小于其邻域点密度,xi为稀疏点。 样本点的相对密度ρ(xi)能够通过计算点之间的距离来计算样本的密度,点之间的距离越大,密度越低;点之间的距离越小,密度越高。而通过ρ(xi)来选择窗宽,能够根据ρ(xi)与数值1之间的大小关系来先判断样本的疏密程度再选取窗宽,从而在低密集区域选择大的窗宽,在高密度区域选择小的窗宽。因此,将相对密度ρ(xi)作为窗宽引入核密度估计的模型中,从而构建相对密度的核密度估计表达式为 (12) 式中:ρ(xi)为不同样本点处核估计的相对密度窗宽,且计算公式为式(11)所示;K(·)为核函数。 由于在实际应用中样本数据都是实时更新的,如果每增加一个样本都对其从头开始计算,那么计算量会随数据的增多变得复杂化。所以,为使核估计的计算性能得到提升,实现核密度估计的实时更新是不可或缺的。 核密度估计的实时更新用已知的n个样本的核估计推导第n+1个样本的核密度估计。推导过程如下: 第n个样本点的核密度估计表示为 (13) 第n+1个样本点的核密度估计为 (14) 式中,ρ(xn+1)为样本点在xn+1处的相对密度窗宽。 由式(3)求得hn为 (15) (16) 式中,ρ(Δxi)(i=1,2,3,…,n)为不同样本点处的相对密度窗宽。 图3 样本特征退化随时间变化的曲线Fig.3 Curve of sample feature degradation over time (17) 当tn+1时刻增加一新样本时,[0,tn+1]的退化量的概率密度函数如下 (18) 当tn+j时刻新增j个样本时,[0,tn+j]的退化量的概率密度函数为 (19) 上文引入相对密度建立核估计的剩余寿命估计模型来保证核估计的平滑性和收敛性。为了消除传统核密度估计的有界偏差问题,本文在自适应相对密度的核密度估计模型的基础上引入核微分同胚变换的方法,通过空间映射的方式对剩余寿命预测模型进行变换,从而解决核函数剩余寿命预测模型在边界上估计的偏差性和无界性。 (20) 式中:K(·)为核函数;hn为带宽;φ为随机变量从区间[a,b]~的微分同胚变换;当x趋于下限或上限时,它的一阶导数φ′(x)趋于无穷。其中,φ(x)和x的关系式为 φ(x):[a,b]→, (21) 设tn为当前时刻,[0,tn]监测时间内采集到的当前样本退化数据,其相应的特征退化随时间退化的特征增量可以作为随机变量Δx∈[0,xth](xth为失效阈值)。 以精神科护士遭受暴力种类、暴力发生频次、暴力应对方式、医院态度等作为自变量,以护士职业倦怠3个维度分别作为应变量,进行多元线性回归分析,分析结果见表5~表7。 从广义角度分析,行政问责制要求国家行政部门的人员在行使权力的过程中秉承对人民负责的原则,坚持以满足人民的根本利益为目的,实现权为民所使、利为民所谋。在行使权力的过程中出现的不良后果,人民都能找到具体的行政主体来承担相应责任。在这个过程中,人民群众是主体,政府是问责对象,政府行政人员在行使权力的过程中接受人民群众的监督和质询并承担对应的责任。从狭义角度分析,行政问责制可应用于行政部门对内部相关行政人员问责的制度。若行政人员在其应负责的工作中有失职情况,行政部门可对相关行政人员问责。通过对失职情况的及时调查并追究相应责任,实现部门内的自我监督进而实现权为民所用。 reach_dist(xi,xj)=max{k_dist(xj),d(xi,xj)} (22) 由上述将有界随机变量转换到实数域上,通过这种空间映射方式,建立微分同胚的核密度估计模型有效减少了边界处的自变量偏移问题。 式中:K(·)为核函数;ρ(xi)为相对密度窗宽。 设tn+t时刻,特征退化量达到xth(见图3)时系统失效。要对当前tn时刻的剩余寿命进行预测,可通过初始时刻到当前tn时刻的退化量x1∶n(记xn=x(tn),x1∶n={x1,x2,…,xn}),推出tn+t时刻的xn+t。设T为设备的剩余寿命,则剩余寿命的概率密度分布函数FT(t)为 贾楠(1983-),女,辽宁省营口人,硕士研究生,毕业于美国天普大学,现有职称:中级经济师,研究方向:经济管理。 通过对已知的单位时间随机退化特征增量核微分同胚估计,用卷积求其特征退化量的概率密度函数,将对数微分同胚变换后[0,tn+t]特征退化量的概率密度记为gd(xn+t) (25) 剩余寿命预测的概率密度为 (26) 在实时监测数据的更新下,tn+t时刻n+t个样本核微分同胚变换的相对密度核估计为 根据式(25)和式(27)可推出 1.1 对象 选取2011年1月—2012年12月在我院儿科实习的全日制护理学生104名,均为女性。其中本科学历38 名,大专学历66 名,平均年龄(20.8 ±1.2),实习时间均为4周。以2011年1—12月实习护生52名为对照组。以2012年1—12月52名学生为实验组,两组学生一般资料比较,差异无统计学意义(P>0.05)。 窗宽h作为影响核密度估计平滑性和核函数宽度的主要因素,当h较小时,核密度估计曲线不够光滑且曲折,表露了较多细节;当窗宽较大时,核密度估计曲线比较平滑,但掩盖了较多细节。因此,选择合适的窗宽对核密度估计是非常重要的。现有的研究中核估计的窗宽分为固定窗宽和自适应窗宽。下面分别对两种窗宽进行介绍,并将其存在的问题进行分析。 对于250 MW等级的发电电动机,电负荷一般选取在700~800 A/cm左右,可以获得合理的利用系数。另外,从控制热负荷、运行稳定域宽考虑,选择360槽方案是比较适宜的。 式中,g(xn+t)为[0,tn+t]特征退化量的概率密度。 在园林绿化施工过程中,花卉移植是一项非常重要的工作。具体指的是将提前培育好的花卉品种根据园林设计的具体情况进行移植,从而达到布景的效果。移植过程通常可以分为2个步骤:起苗和栽植。栽植过程也被称为定植过程。有些花卉由于在移植过程中容易死亡,因此可以通过有性繁殖的方式,提前在容器或者苗床内完成育苗工作,为后续的定植提供便利条件。具体的栽植方式又可以分为有土和无土2种[3]。 从而能够推出tn时刻系统剩余寿命预测的概率密度函数为 (29) 随着实时监测的进行,监测到的样本数据不断增多,样本的核密度估计也随着不断更新,采用非实时的寿命预测模型时,每新增一个样本数据,基于这些样本的核密度估计都要重新计算,这样会造成历史样本不断重复计算,计算量也会越来越大,为避免实时监测系统中样本核密度估计不断重复计算的问题,提出对核密度估计模型实时更新的递推算法,进而实现对特征退化分布和实时剩余寿命的不断实时更新。 以齿轮箱的齿轮为研究对象对本文模型进行验证,图4为齿轮试验台架,其中心距为150 mm,电机转速为1 200 r/min。本试验过程主要是针对加速度传感器的振动信号进行监测。 图5介绍了各个传感器的分布,1#~8#为加速度传感器(4#装设在轴承座的径向);在主试箱和陪试箱的正上方40 cm处安装了9#和10#为声音传感器;齿轮箱的温度是通过主试箱内的11#温度传感器来测。采用快速测定法,加载了八级载荷,在第八级载荷发生断齿。本试验主要对4#传感器记录齿轮箱在第八级载荷的加速度数据进行分析。采样频率为25.6 kHz,每次持续60 s,每9 min记录一次数据。 为了能够更好的展现退化趋势,可通过采用均方幅值方法对数据进行特征提取,减少后期预测中的误差。求得采样信号的均方幅值为 (30) 式中:n为采样点数;yj为初始振动信号;yi为均方根幅值。 图6为特征值随监测时间变化曲线。由图6可看出,该特征提取方法可以很好的把齿轮箱退化趋势展示出来。 图6 特征值随监测时间变化曲线Fig.6 Curve of characteristic values changing with monitoring time 由图6知,在t∈[0,10]h时,齿轮处于啮齿阶段;t∈[10,68]h时,特征值逐渐增大,齿轮进入正常磨损;t∈[68,77]h时,齿轮磨损加剧,在77.17 h发生断齿,此时齿轮的故障阈值为y=76.325 mm/s2。 5.1.1 自适应相对密度窗宽的确定 通过前文提出的自适应相对密度方法对核密度估计的窗宽进行选取。图7给(a)~图7(c)分别给出了t=40 h,t=70 h,t=77 h三个不同时刻样本点的相对密度窗宽选取。图中:“o”为特征退化增量样本值;“*”为相对密度窗宽值从而可看出,随着样本数据的增多,相对密度窗宽方法能够自适应的选取窗宽,在不同样本密度下能够选择出合适的窗宽。 图7 不同时刻样本相对密度窗宽的选取Fig.7 Selection of window width of relative density of samples at different moments 5.1.2 齿轮的实时剩余寿命预测 用本文模型对齿轮实时剩余寿命预测,得到图8所示的自适应相对密度核估计的剩余寿命预测估计值与实际值在实时监测系统下不同监测时间的比较图。其中,剩余寿命预测值通过平均剩余寿命求得 (31) 由图8分析可得,在初始阶段由于样本数据少,剩余寿命的预测值与实际值之间的误差较大;随着监测时间的变化,样本的增多,剩余寿命的概率密度越来越高,越来越窄,方差逐渐越小,预测值逐渐贴近实际值,表明预测的剩余寿命愈加准确。(图8中:‘*’为估计值;‘o’为实际值) 图8 不同监测时刻的概率密度函数Fig.8 Probability density function at different monitoring moments 为了更加清楚地分析不同时刻剩余寿命的概率密度比较,表1给出了本文所提方法的剩余寿命预测值和实际值的均方根误差。由表1中数据可以分析出,在监测系统的实时更新,随着样本数据的不断增多,预测值与实际值之间的误差逐渐变小,验证了本文方法的可行性。 表1 剩余寿命预测值与实际值的比较Tab.1 Comparison of predicted and actual values of remaining life 5.1.3 基于固定、积分均方误差和相对密度三种窗宽准确性比较 在实时监测系统下,随着数据的不断变化,要使选择的窗宽能够满足自适应地在密度小的区间选择较大的窗宽,在密度大的区间选择较小的窗宽。 图9和图10分别给出了监测时间t=40 h和t=70 h时基于固定窗宽、自适应大拇指法则窗宽与自适应相对密度窗宽三种窗宽的核估计概率密度的比较(图中:‘*’为估计值;‘o’为实际值)。 图9 t=40 h的核估计概率密度比较Fig.9 Comparison of kernel estimate probability density for t=40 h 图10 t=70 h的核估计概率密度比较Fig.10 Comparison of kernel estimate probability density for t=70 h 由图可知,基于自适应相对密度窗宽的方法与其他两种窗宽的方法相比,其结果更接近实际值。随着监测时间的变化,样本数据的不断增加,三个窗宽下的剩余寿命估计值与实际值之间的误差会逐渐变小,而本文相对密度窗宽的方法相较于其他方法预测结果的误差相对更小。从整体分析来说,本文所提的相对密度窗宽在核估计时可以更好的将数据拟合,并能更加准确的对概率密度函数进行估计,从而使剩余寿命预测的可靠性和准确度进一步提高。 5.1.4 核估计的边界偏移问题 在剩余寿命预测上,为了消除核估计的边界偏移问题,对有界随机变量进行对数核微分同胚变换将定义域转化到实数域上,再用核密度估计进行概率密度估计,从而提高预测的准确性。图11和图12给出在t=40 h和t=70 h两个不同时刻下本文提出模型与传统核密度估计模型在核估计的偏差问题的比较。 图11 t=40 h的核估计偏差比较Fig.11 Comparison of kernel estimation deviations for t=40 h 从图中可以看出,两个不同时刻都反映出传统核密度估计存在有界性产生的边界偏差问题,而本文提出的方法经过核微分同胚变换将定义域转化到实数域上,有效的消除了核估计的边界偏差。因此,本文提出的模型能够有效解决边界偏移问题,提高了剩余寿命预测可靠性和准确性。 图12 t=70 h核估计偏差比较Fig.12 Comparison of deviation of kernel estimation for t=70 h 5.1.5 不同模型比较 目前在机器学习的剩余寿命预测方法中LSTM神经网络方法对于故障时间序列有着较好的预测效果;Gamma过程和Wiener过程是两个最常用随机过程退化建模的方法,在寿命预测建模中应用较多。因此,为了验证本文模型的精确度,采用上述三种方法与本文模型进行比较分析。 (1)采用Zhang等的LSTM神经网络方法对齿轮进行了剩余寿命预测。图13(a)为周期数为420(10 min),即70 h时预测的剩余寿命结果,在周期数为455(10 min)时,达到阈值76.325 mm/s2,故其预测的剩余寿命为455-420=35(10 min)=5.83 h。图13(b)为周期数为450(10 min),即75 h时预测的剩余寿命结果,在周期数为456(10 min)时,达到阈值76.325 mm/s2,故其预测的剩余寿命为456-450=6(10 min)=1 h。与本文模型具体的结果比较见表2。 图13 LSTM模型不同时刻的剩余寿命预测Fig.13 Residual life prediction of LSTM model at different times (2)齿轮的退化是一个持续累积退化的过程,Gamma过程由于具有非负、增长、独立增量的属性,被广泛用于逐渐累积损伤过程的退化建模中。为进一步测试本文模型的准确性,在相同条件下,采用基于Gamma过程的剩余寿命预测方法进行比较说明。图14(a)和图14(b)分别是监测时间t=60 h和t=70 h时两种模型的剩余寿命概率密度(图中:‘*’为预测值;‘o’为实际值)。 图14 不同时刻下本文模型与Gamma过程的比较Fig.14 Comparison of the model and Gamma process at different time point 通过图14可分析出,本文模型方法相对于基于Gamma过程的方法来说,其剩余寿命的概率密度函数的方差愈来愈小,可以更好地反映样本数据,预测值更加贴近真实值。t=70 h时能够明显看出本文方法的预测值更接近实际值。因此,本文模型在剩余寿命预测的应用上更加准确有效。 (3)Wiener过程模型多用于对具有非单调退化过程的设备进行建模。在相同条件下采用Zhai等研究中Wiener过程模型对齿轮的剩余寿命进行预测。图15(a)和图15(b)分别给出了监测时间t=60 h和t=70 h时本文模型和Wiener过程模型的剩余寿命概率密度比较。 由图15可以看出,本文模型与维纳过程模型相比,剩余寿命的概率密度函数的方差愈来愈小,预测值更加贴近真实值,预测的准确性提高。 此外,通过引入相对误差指标进一步量化预测的精确度,给出监测时间在t=60 h,t=65 h,t=70 h,t=75 h,t=77 h五个时刻下四种方法的比较结果。 图15 不同时刻本文模型与Wiener过程模型的比较Fig.15 Comparison between the model in this paper and Wiener process model at different times 通过表2可知,在不同时刻的相对误差比较下,四种模型的剩余寿命预测结果都逐渐趋于真实值,而本文模型的预测结果与LSTM模型、Gamma过程以及基于Wiener过程三种方法相比,其相对误差更小,从而验证了本文模型的优越性。 表2 不同监测时刻下相对误差的比较结果Tab.2 Comparison results of relative errors at different monitoring times 为验证本文方法的有效性,利用IEEE PHM2012提供的轴承全寿命数据对模型进行验证。本文以转速为1 800 r/min,载荷为4 000 N工况下的Bearing 1-1的全寿命振动数据为例进行分析。该数据来源于FEMTO-ST研究中心PRONOSTIA试验台对滚动轴承的加速寿命试验,振动信号的采样频率为25.6 kHz,10 s采集一次,一次采集0.1 s,即一次采集2 560个样本点。 通过均方幅值法处理Bearing 1-1的全寿命振动数据,如图16所示的特征值随监测时间变化曲线。从图16可以看出,均方根随时间基本呈现单调增加的趋势,能较好地反映其退化趋势,该轴承在t=2.749×104s时磨损开始加剧,且在t=2.803×104s时失效,均方根的失效阈值为5.607 mm/s2。 图16 特征值随监测时间变化曲线Fig.16 Curve of characteristic values changing with monitoring time 采用本文模型对轴承进行剩余寿命预测,由图17可知,随着系统运行时间的增加,接收到的监测样本不断增多,基于相对密度核估计的剩余寿命的概率密度不断实时更新,剩余寿命的概率密度变窄变高,方差越来越小,说明预测的准确性不断提高。 图17 不同监测时刻的概率密度函数Fig.17 Probability density function at different monitoring moments 为进一步对本文提出方法的预测效果进行评估,表3给出了对不同监测时间,实际剩余寿命、本文模型预测的平均剩余寿命的均方根误差(root mean square error,RMSE)比较。 从表3可以看出,随监测时间的增加,RMSE呈现逐渐减小的趋势,且随着监测数据的增多,预测的剩余寿命与真实寿命的误差更小,说明本文模型预测的剩余寿命更接近实际的寿命值。 表3 剩余寿命预测值与实际值的比较Tab.3 Comparison of predicted and actual values of remaining life 本文针对核密度估计在设备剩余寿命预测时,由于在监测数据分布不均匀区域选择的窗宽不够准确和核估计模型中随机变量的有界性产生的边界偏差,从而导致预测的不准确,提出一种基于相对密度的核估计实时剩余寿命预测方法。该模型将k近邻思想计算出的样本点的相对密度作为核密度估计的窗宽,不仅解决了固定窗宽由样本数据分布不均导致拟合不足的问题,而且能够对任意形状,密度不均匀的数据集自适应地选择出更加准确的窗宽,提高了拟合度。在核估计的边界偏差上,引入核微分同胚变换的方法有效的消除了核密度估计带来的边界偏差问题。此外,随着样本的增加,为了避免核密度估计的重复计算,建立了基于相对密度核估计的实时更新模型。实例分析表明,随着样本数据的增加,剩余寿命的预测越来越接近实际值,方差变得越来越小,提高了预测的准确性;并且通过与LSTM模型、基于Wiener过程以及基于Gamma过程的预测方法比较,进一步验证了本文模型的准确性和有效性。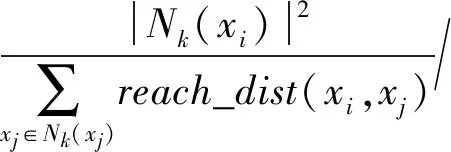

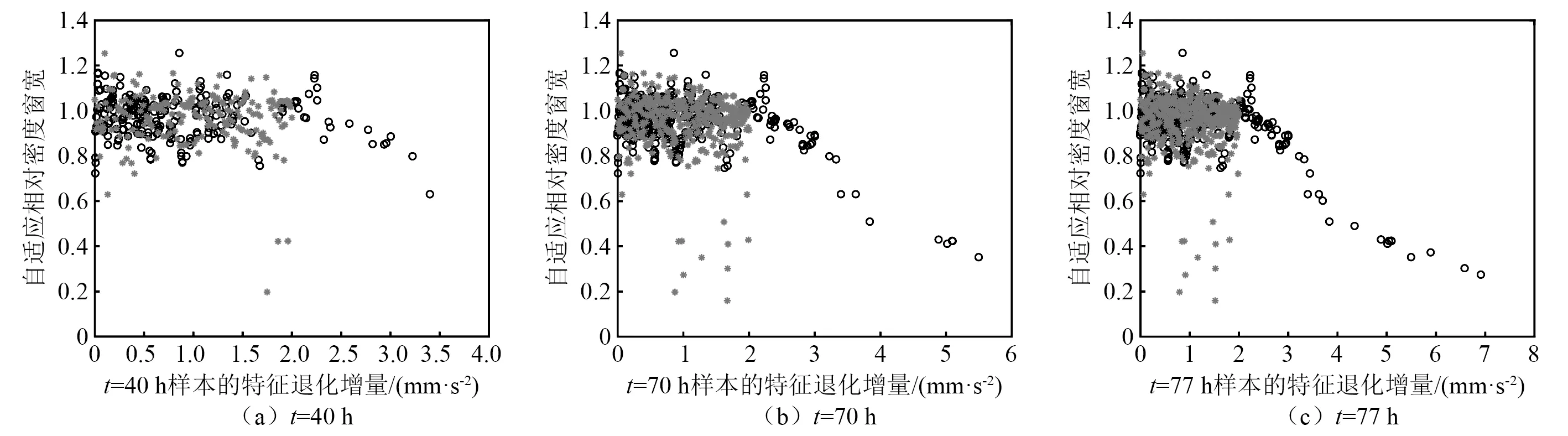
2.2 自适应相对密度窗宽的确定
2.3 自适应相对密度窗宽的实时更新
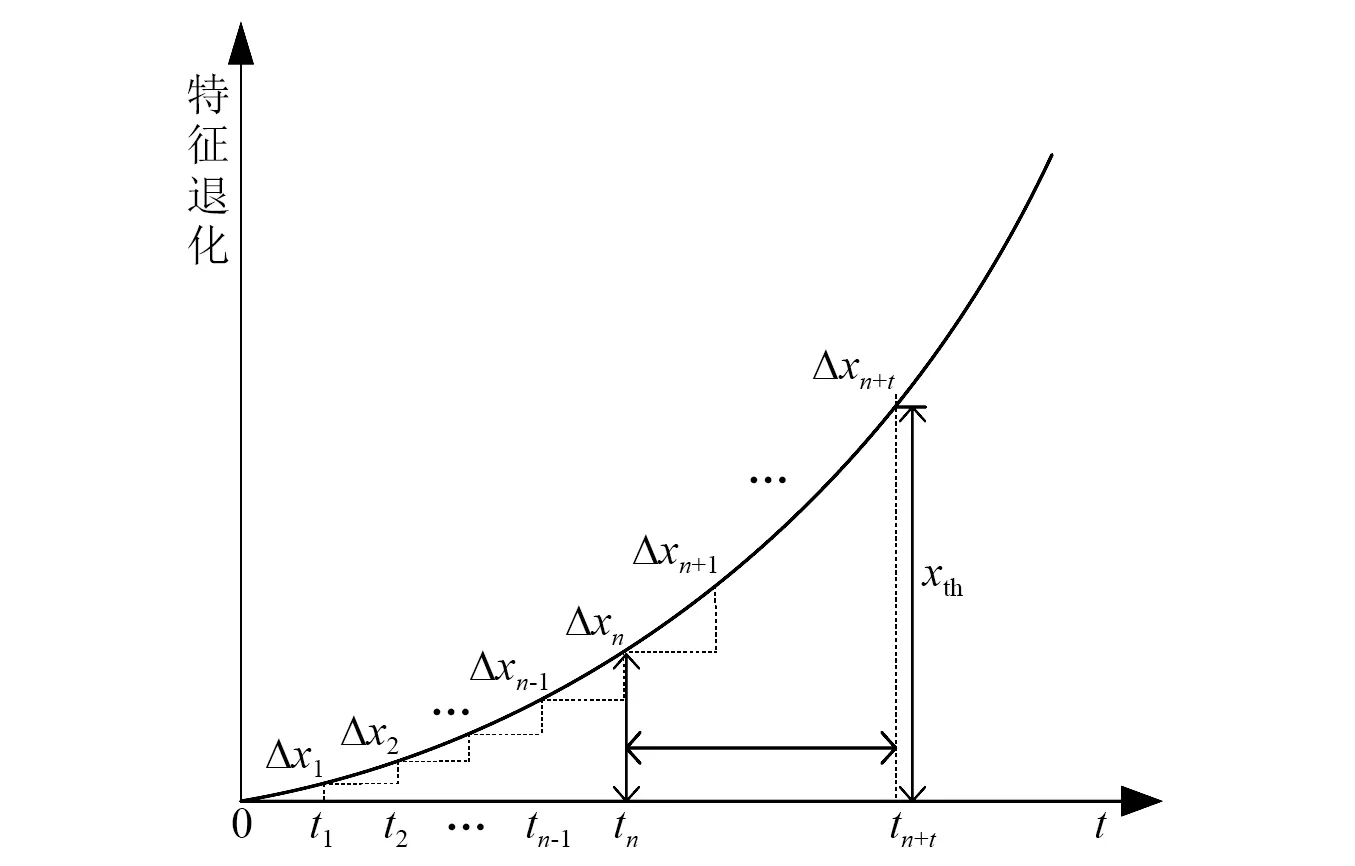
3 特征退化分布的计算
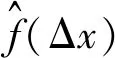
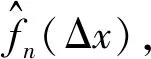
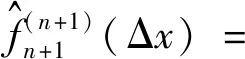
4 剩余寿命预测模型
4.1 核微分同胚估计

4.2 核微分同胚估计的剩余寿命预测模型

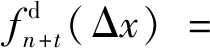
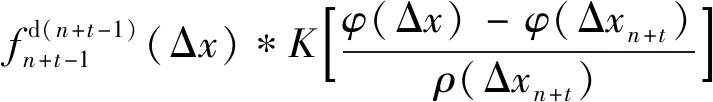
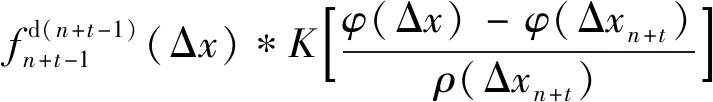
5 实例分析
5.1 齿轮磨损试验

5.2 滚动轴承的加速寿命试验

6 结 论
