气动调节阀最优分数阶PID控制器设计

朱 敏，臧昭宇，胥子豪，肖 阳

(合肥工业大学 电气与自动化工程学院，合肥 230009)

气动调节阀作为自动化系统中关键的终端设备，被广泛应用于金属冶炼、石油化工、核电、污水处理等工业控制领域[1-2]。气动调节阀由于其密封性能、摩擦力、流量特性曲线等自身固有属性，使其难免具有滞后、死区等非线性特性[3]。在工业生产过程中，若阀位控制不当使得震荡过大，会加大阀杆磨损，严重时会造成喘振，减小调节阀寿命。若调节时间过长则不利于生产效益。气动调节阀不仅需要快速平稳的到达指定阀位，还需要有较高的精确性。

针对气动调节阀的阀位控制，国内外学者们也做了诸多的工作。Plestan等[4]设计了一种新的自适应滑模控制器，控制器确保增益不被高估，并减小了阀位控制过程中的抖振。Zabiri等[5]将预测控制应用到气动调节阀中，尽管在某种意义上解决了调节阀非线性因素干扰，但仍存在鲁棒性差、稳定性低的问题。Guo等[6]根据阀缸伺服系统特点设计了一种自抗扰控制器，通过AMESim与MATLAB的联合仿真验证了控制器具有抗干扰性强、精度高的优点。吴朋等[7]将仿人智能控制应用到阀位控制中，结果表明控制器对被控对象参数变化不敏感。此外，模糊神经网络-PID[8]、PID-IMC(internal model control)[9]、Expert-PID[10]等也被提出用于调节阀阀位控制，在一定程度上提高了调节阀的控制精度和响应速度。目前工程中大多控制策略仍主要为整数阶PID或基于整数阶PID的其他控制策略，而传统的整数阶PID已难以满足日益增长的控制需求。

在已有的文献中，少有研究人员将分数阶控制理论应用到气动调节阀阀位控制中，由于分数阶微积分运算具有记忆特性，且相对于整数阶PID引入了微分阶次μ与积分阶次λ，增加了控制器的设计的灵活性，将分数阶计算与控制器参数整定结合是目前的研究热点之一[11-12]。分数阶PID控制器参数整定主要方法有智能优化法[13]、相角裕度和幅值裕度法[14]、主导极点法[15]以及基于理想bode传递函数设计法[16]等。部分学者引入智能优化算法调整分数阶PID参数，结果显示具有良好的效果[17-19]。例如，量子粒子群算法作为粒子群算法的变体，已被证明具有高随机性和全局收敛性[20]。

为有效实现调节阀阀位控制，本文提出一种改进的量子粒子群算法，通过引入混沌映射和非均匀高斯变异增强算法寻优能力，标准的气动调节阀模型由于未考虑气源气压波动、系统黏滞和死区等而不够精确，因此本文采用改进的量子粒子群算法拟合控制系统开环响应曲线，并推导新的气动调节阀模型。另外，将分数阶PID控制方法应用于气动调节阀阀位控制中，并通过所提出的改进算法整定分数阶PID控制器参数。最后，通过仿真和试验证明了所提出的调节阀阀位控制方法的有效性。

1 气动调节阀数学模型

1.1 气动调节阀结构和工作原理

气动调节阀主要由三部分构成：阀门定位器、阀执行器以及调节阀阀体。其结构示意图如图1所示。阀门定位器阀体为调节阀的“大脑”，对控制信号进行运算并发送气压信号给执行机构修正阀位。阀执行机构作为执行器，在气压作用的信号下调整阀位，直到气室达到平衡状态。阀体通过阀芯和阀座组成节流件，以此实现流量和阀位的对应关系。

气动调节阀工作原理为阀门定位器接收阀位设定信号，控制器将阀位设定信号和已采集的阀位反馈信号实时运算处理，阀门定位器输出信号不能直接驱动阀执行器，需要由定位器中的电/气转换单元转换为气压信号，转换后的气压信号经过气动放大器放大后由控制气压气路进入腔室，改变腔室气压并推动薄膜产生推力，推动执行机构(即阀执行器)中阀杆动作，在理想情况下，当阀位反馈信号和预设信号相等时，执行机构腔室内薄膜处于平衡状态，此时阀位便达到了指定位置。

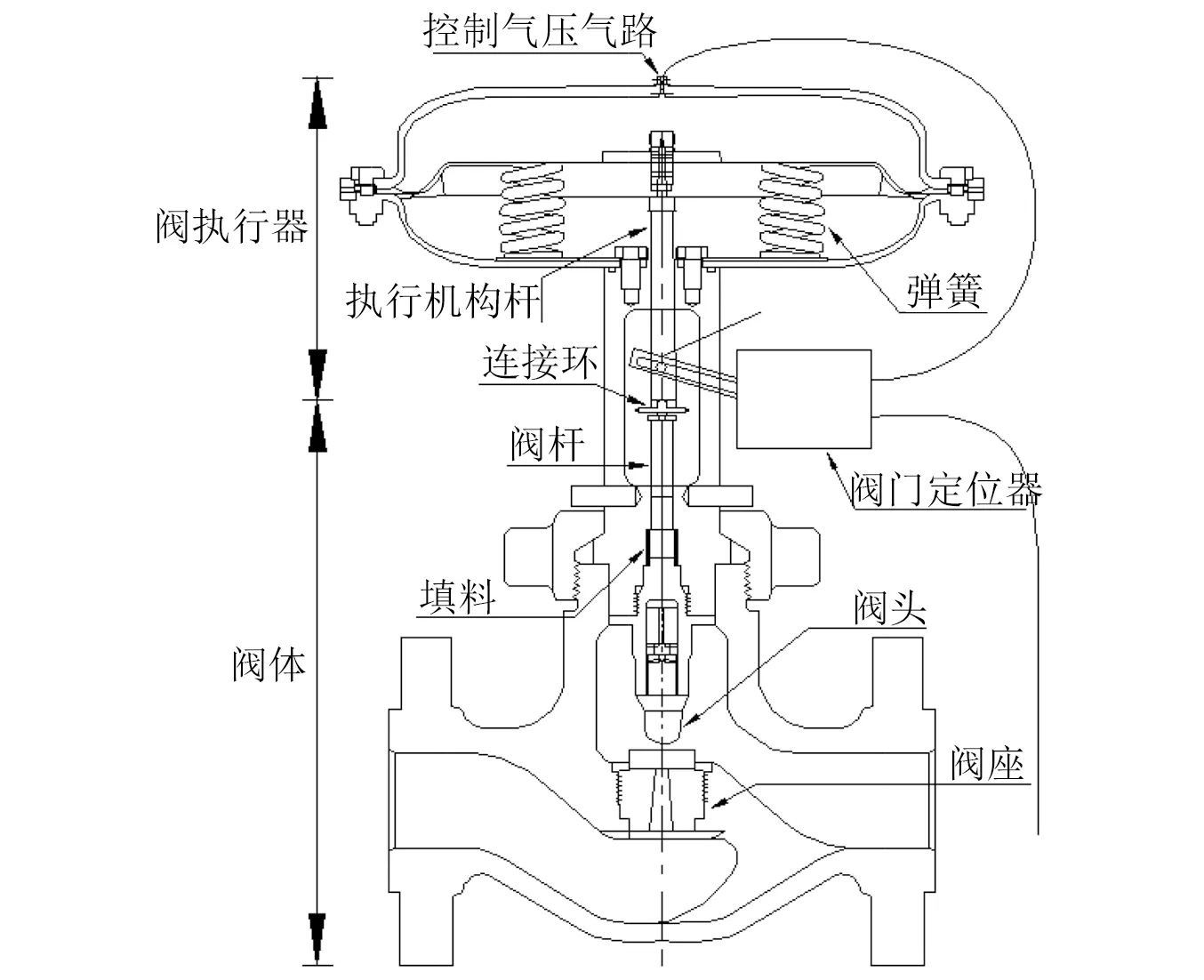
图1 气动调节阀结构图Fig.1 Structural of pneumatic control valve

1.2 气动调节阀模型

气动薄膜执行器分为阀执行器机构和调节机构，阀执行器机构工作过程分为输入气源气压转换为气室内气压、气室气压转换为推力以及推力转换为阀杆位移三个阶段。其中后两个环节可看作为线性环节处理。阀执行器数学模型微分方程近似为

(1)

式中:P1为输入气源气压；P2为腔室气压；Kr为弹簧刚度；Ae为腔室内膜片有效面积；R为气路气阻；C为气路气容。

调节机构杆由弹簧结构驱动，对阀杆进行受力分析，腔室气体对腔室薄膜上的压力与阀杆重力之和大于阀杆受到的摩擦力和弹簧弹力之和时，阀杆向下滑动。由牛顿第二定律有

ma=Fm+Fp-Ff-Fd-Fs-Fvc

(2)

式中:Fm为阀杆所受重力；Fp为腔室压力；Ff为阀杆所受静摩擦力；Fd为弹簧预紧力；Fvc为介质反作用力；Fs为弹簧反作用力，忽略弹簧预紧力和反作用力，展开式(2)有

(3)

式中：m为阀杆质量；g为重力加速度；p为腔室压强；Kb为阀杆库伦摩擦因数；Kf为弹簧刚度系数。

阀门定位器主要由力矩马达、喷嘴挡板及气动放大器组成。其中力矩马达包含线圈电路和磁性单元，其输出力矩Td和挡板偏转角θ关系简化为

Td=KtΔi+Kmθ

(4)

(5)

(6)

式中：Kt为力矩马达电磁力矩系数；Km为力矩马达磁弹簧刚度；Δi为输入电流；Nc为线圈匝数；φg为初始零位磁通量；a为力矩的力臂长度；g为铁片在中间位置的气隙宽；ξ为磁路中磁阻对力矩马达影响系数。

喷嘴挡板的节流口与挡板之间距离由力矩马达输出转角决定，喷嘴挡板的流量特性简化为

(7)

式中：ρ为流体密度；Ps为气源气压；QL为喷嘴挡板流量；Cq为流量系数，一般取0.6～0.8；D0为节流孔直径；Df为喷嘴孔径；xf为挡板到平衡状态的偏移量。

气动放大器对喷嘴挡板的输出气压放大，使气体进入薄膜气室驱动阀杆运动。充气和排气的工作过程可用小孔流量特性等价。阀开口处流量方程为

(8)

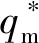
2 量子粒子群算法及改进

2.1 标准量子粒子群算法

Sun等[21]将量子学和群体智能相结合，提出了具有量子行为的粒子群优化算法(quantum particle swarm optimization,OPSO)。相较于标准粒子群算法(particle swarm optimization,PSO),QPSO算法中的粒子的轨迹和速度并不确定，粒子在空间中某点出现的概率密度由波函数ψ(X,t)的平方表示，由薛定谔方程求解粒子在空间中某点出现的概率密度函数，再通过Monte-Carlo随机模拟测量粒子位置。设粒子规模为M，第i个粒子在t+1时刻位置Xi(t+1)为

(9)

Pi(t)=φ·Xib(t)+(1-φ)·Xgb(t)

(10)

Li(t)=2α·|C(t)-Xi(t)|

(11)

(12)

(13)

式中：Pi(t)为第i个粒子的吸引子；Li(t)为势阱特征长度；ui(t)和φ为[0,1]的随机数；Xib为第i个粒子t时刻的最优位置；Xgb(t)为t时刻群体全局最优位置；C(t)为所有粒子最优位置的平均值；Tmax为最大进化次数；α为收缩-扩张系数，多数情况下采用线性减小方式可取得较好效果。

2.2 混沌优化算法

混沌系统具有随机性和遍历性，可以通过迭代覆盖目标区域所有点，并最终逼近最优解。为减小QPSO算法陷入局部最优可能性，引入混沌映射序列。混沌系统Logistic映射方程为

Zt+1=μZt(1-Zt)，t=1,2,3,…

(14)

式中：Zi∈(0,1]，为迭代t时刻混沌向量；μ为混沌变量，当μ=4时，模型为完全混沌状态。由t时刻第i个粒子位置Xi(t)和Pi(t)距离确定混沌映射关系，并根据迭代调整每一代粒子的混沌搜索范围。

(15)

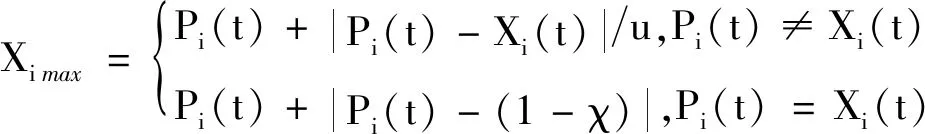
式中,u,χ∈(0,1)。再由式(17)将粒子Xi(t)归一化，求得混沌向量初值Ri,1。

(17)

由混沌映射结构得到混沌向量集合Ri=(Ri1,Ri2,…,Rim)，m为混沌向量个数。由式(18)使混沌向量反变换到原始空间。

H[Xi,r(t)]=Xi min+Ri,r(Xi max-Xi min)

(18)

最后选择效果最优的粒子为下一代粒子，迭代公式为

(19)

2.3 非均匀高斯变异

混沌映射和变异操作都是增加种群多样性的方法，前者是在粒子初始化时进行，后者则是在粒子优化过程中进行。本文为适应度为后20%的粒子,设计一种非均匀高斯变异方法，更新公式为

C′(t)=C(t)+Δ[t,Gi(t)]

(20)

(21)

Gi(t)=N{[Xgb(t)-Xi(t)],σ}

(22)

式中：Δ[t,Gi(t)]为通过高斯分布Gi(t)自适应调节步长的变异算子;b为决定变异非均匀程度的系统参数，一般取2或5[22]；r为[0,1]区间随机数;σ为高斯分布标准差。当迭代次数t增加，函数Δ(t,y)返回值就会变小，即非均匀变异算子随着迭代次数变化调节变异尺度，前期变异尺度大，搜索较大范围以发现可能的潜在区域；后期变异尺度小，加强局部搜索能力。

3 气动调节阀模型辨识

气动调节阀集气路、电路及磁路于一体，控制系统复杂，其白箱模型往往未考虑到调节阀的黏滞、磨损等情况且需要大量准确的参数；当模型和实际过程有所偏差时，还需对实际过程数据进行补偿。对气动调节阀做开环阶跃试验，将结果归一化，其试验结果如图2所示。

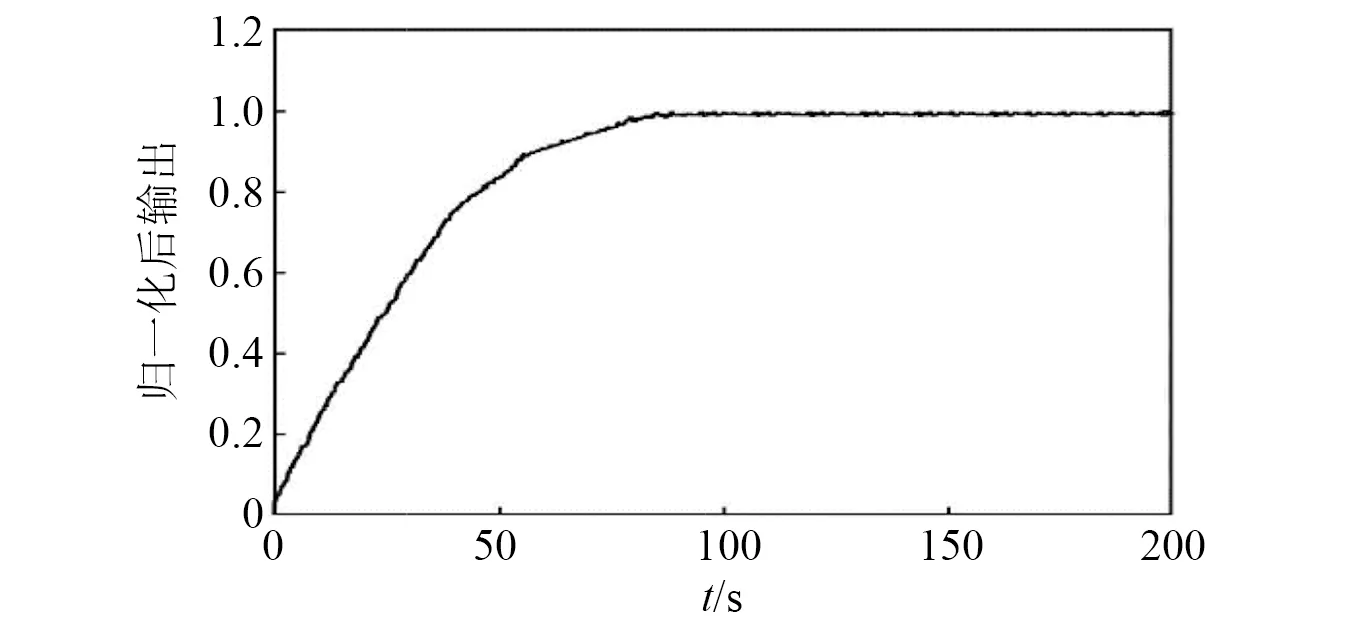
图2 调节阀辨识结果Fig.2 Identification results of control valve

气动调节阀模型往往以三阶传递函数形式表示[23]，为建立有效的模型，通过本文改进量子粒子群算法辨识传递函数，在每次迭代中，将模型阶跃响应与试验数据比较，并将差值作为算法适应值，流程图如图3所示。

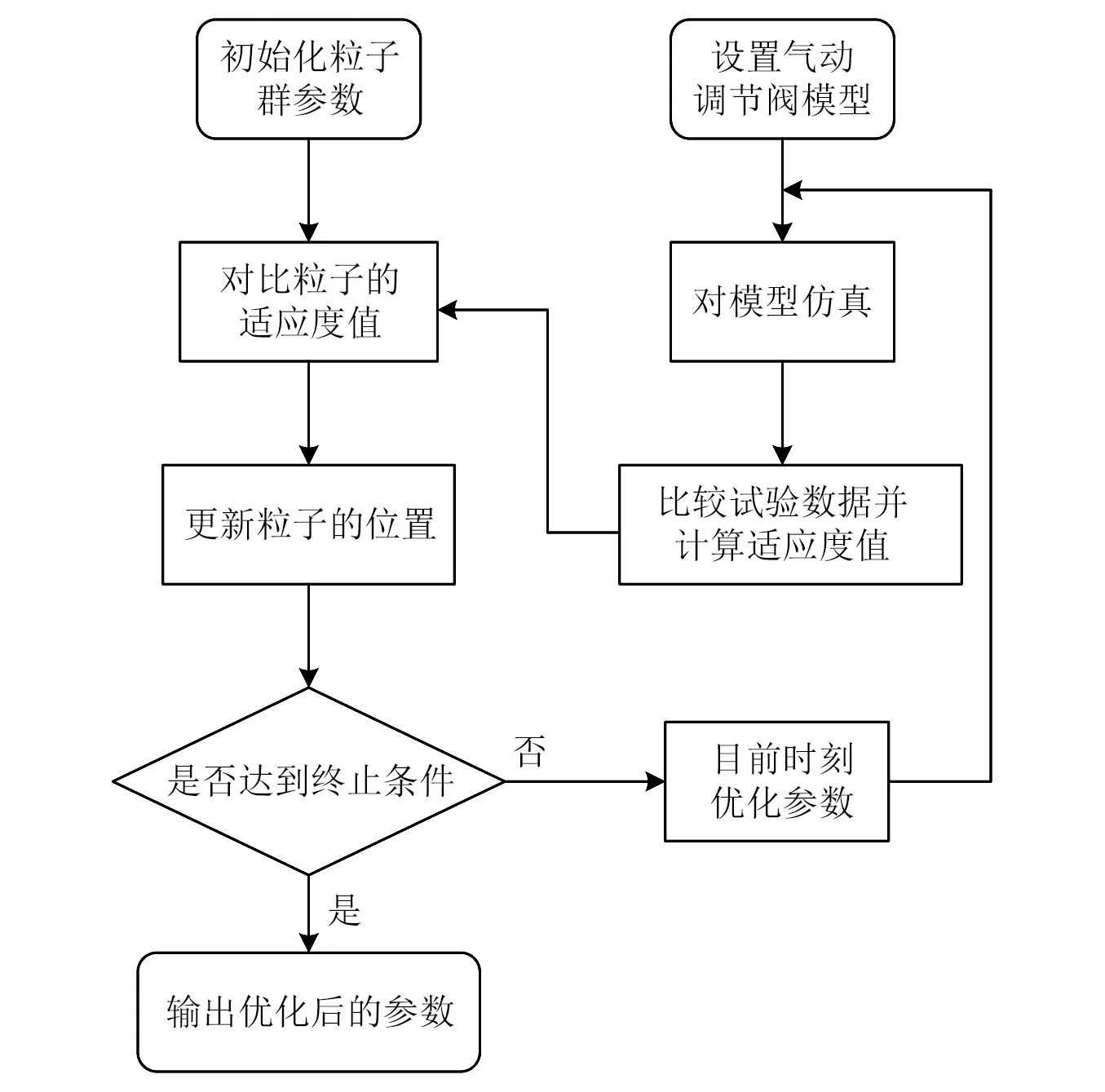
图3 改进量子粒子群算法辨识模型流程图Fig.3 Flow chart of identification model based on IQPSO algorithm

多次迭代后，得到气动调节阀模型G(s)为

为检验模型是否准确，通过均方根误差(root mean square error,RMSE)衡量模型准确性，公式为

(24)

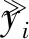
表1 四种不同算法辨识准确性对比Tab.1 Comparison of identification accuracy of four different algorithms

由表1可见，提出改进的量子粒子群算法均方根误差最小，其拟合程度最高，表明了改进算法的有效性和优越性。

4 分数阶PID控制器设计

4.1 分数阶PID控制器

目前常用分数阶微积分定义有三种：Riemann-Liouville、Grunwald-Letnikov和Caputo定义。在一定条件下前两种定义基本等效，其中Grunwald-Letnikov定义为

(25)

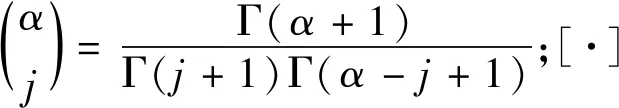
(26)

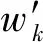
K=(wh,wb)δ

(27)

(28)

(29)

式中，δ为分数阶阶次。设定wb=0.001，wh=10 000，N=5。PIλDμ比整数阶PID多了积分阶次λ和微分阶次μ，可以更灵活的控制被控对象，从而满足复杂系统性能指标。图4为PIλDμ控制平面图。

图4 分数阶PID控制平面图Fig.4 Fractional order PID control plan

图5为PIλDμ控制系统模型。r(t),u(t)和y(t)分别为期望输入、控制器输出和系统输出；G(s)为被控对象。

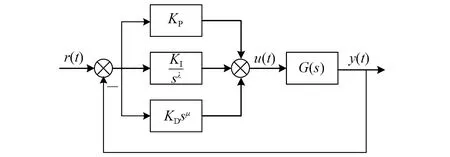
图5 分数阶PID控制系统模型Fig.5 Fractional order PID control system model

分数阶PID控制器传递函数为

(30)

4.2 分数阶PID控制器的参数整定

本文根据阀门控制系统的阀门开度输出信号设计性能指标，将KP,KI,KD,λ和μ作为单个粒子5个分量，在5维空间中寻优计算。

通过适应度函数的值判断参数寻优结果的好坏，选取ITAE性能指标(系统的绝对值误差和时间的积分)，可以反映系统的精确性和快速性，同时可兼顾较小超调量以尽量避免阀位超调；将控制器输出平方项加入适应度函数以避免输出量过大。适应度函数为

(31)

式中：e(t)为控制误差;u(t)为控制器输出量;λ1和λ2为权重系数,λ1和λ2分别取0.999和0.001。

改进量子粒子群算法优化分数阶PID参数步骤如下：

步骤1对粒子群规模M、寻优维度D、最大迭代次数Tmax和混沌变量μ等进行初始化。

步骤2由适应度函数计算粒子初始适应度值，求解粒子的全局最优值以及其对应的最优位置。

步骤3由式(10)计算粒子的吸引子不动点，并对粒子位置进行限制。

步骤4将种群中粒子适应度值由高到低排序，对适应度值差的粒子进行非均匀高斯变异，并再次更新全局最优适应度值及其对应的最优位置。

步骤5使用混沌优化算法扩大优化变量的取值范围，由当前最优解位置产生混沌序列。根据适应度值判断是否出现更好的位置，若出现更好位置，则使其取代原最优位置。

步骤6判断是否达到最大迭代次数Tmax或达到搜索精度要求，都不满足则使迭代次数加一，返回步骤2再次执行，直至达到终止条件。

5 仿真验证

为检验改进量子粒子群算法优化PIλDμ参数的效果，使用式(23)传递函数，利用Simulink搭建控制模型。设置标准PSO、标准QPSO以及IQPSO算法种群规模M=60，最大迭代次数Tmax=100，分数阶PID参数取值范围为：KP1∈[0.01,300]，KI∈[0.01,300],KD∈[0.01,300],λ∈[0.01,2],μ∈[0.01,2],给定系统输入为单位阶跃信号。将标准PSO算法、标准QPSO算法以及IQPSO算法三者各进行20次试验，取最优值作为参数对比，得到适应度值曲线如图6所示。

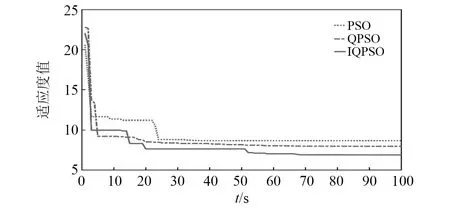
图6 不同算法最优个体适应度变化Fig.6 Variation of fitness of optimal individuals in different algorithms

如图6所示，标准PSO算法和标准QPSO算法最优适应度值分别在26代和64代基本不再改变，相比较于标准PSO和标准QPSO,IQPSO收敛速度较快，可以更好地跳出局部最优值，即寻到的参数更优，因此IQPSO具有较高的搜索精度和收敛速度。

将三种方法优化后的PIλDμ参数值进行阀门开度控制的仿真试验，取优化后最优适应度值下控制参数，在单位阶跃输入下进行仿真试验。结果如图7所示。

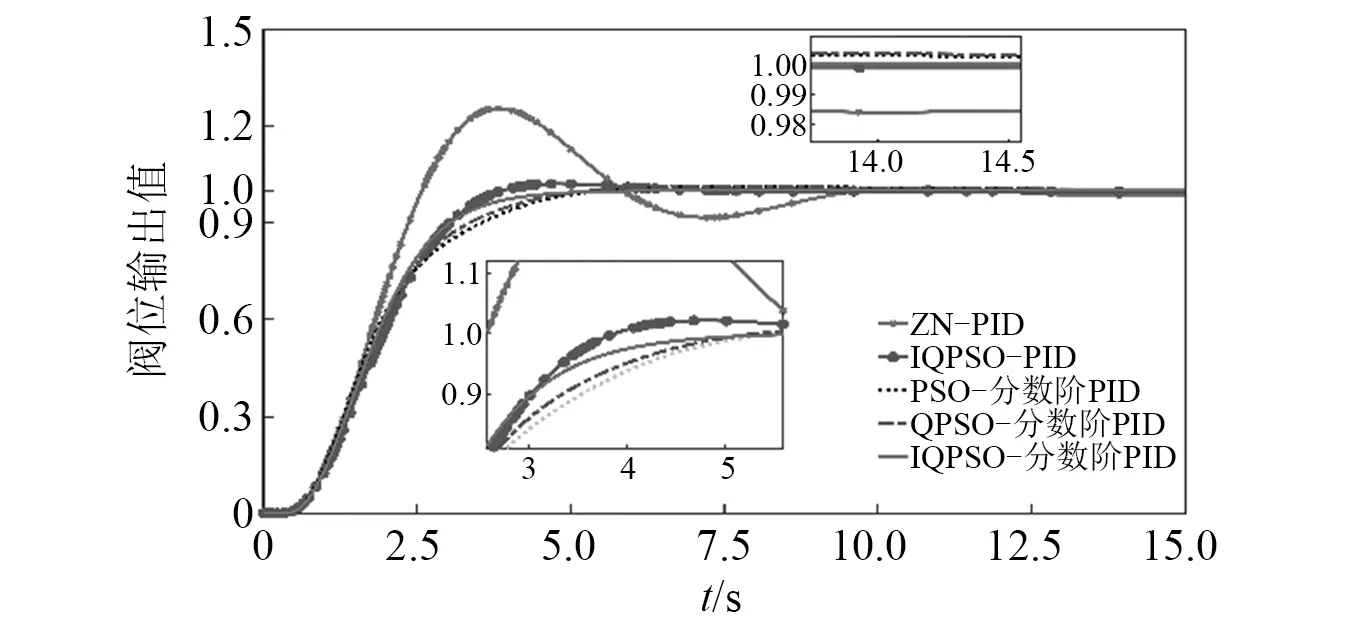
图7 不同算法的阶跃响应对比Fig.7 Comparison of step response of different algorithms

将五种算法的超调量、调节时间和稳态误差三项性能指标进行对比并得出如表1所示结果。

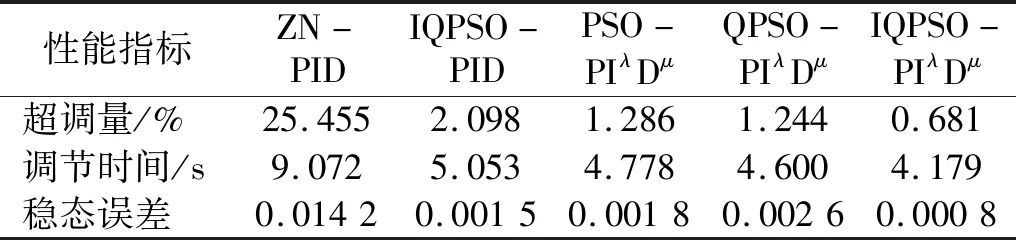
表2 五种算法性能指标对比Tab.2 Performance comparison of five algorithms

通过图7和表2可以看出，相比于另外四种优化后算法，IQPSO优化PIλDμ算法有着超调量小、调节时间短以及稳态误差低的优点，另外，从表2也可以看出，在相同算法的参数优化下，相比较整数阶PID，PIλDμ稳态误差更小，超调量降低，具有更优的动态性能。

为进一步验证控制算法的性能,以一组正弦信号为y=sin(0.4t)作为仿真系统的期望阀位开度信号，图8为阀位开度控制系统在五种不同算法作用下对目标阀位的跟踪控制系效果，可得出IQPSO优化PIλDμ后的算法对调节阀阀位的跟踪控制具有更好效果。

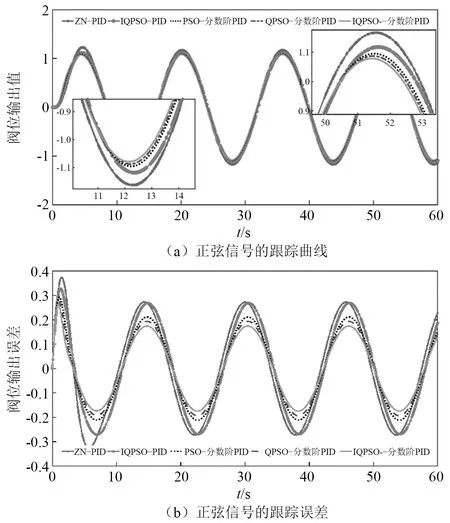
图8 不同算法的控制作用下正弦跟踪曲线及跟踪误差Fig.8 Sinusoidal tracking curve and tracking error under the control of different algorithms

6 试验验证

为检验分数阶PID控制器有效性，建立气动调节阀试验平台，通过上位机LabVIEW图形化编程软件分别编写两种不同的控制器算法，试验平台设备装置如图9所示。

1.去除控制器的阀门定位器；2.气动薄膜调节阀；3.电位器接口；4.减压阀；5.USB5633数据采集卡；6.开关电源；7.工控机；8.显示屏；9.分离净化器；10.空气压缩机。图9 试验设备及装置Fig.9 Experimental equipment and devices

图9设定气动调节阀工作压力为0.6 MPa，由USB5633采集阀门定位器反馈电压信号，并向其输出0～5 V的电压信号以驱动调节阀阀杆运动。

分别以阶跃、正弦波和方波信号作为输出期望阀位，分别用整数阶PID控制器和分数阶PID控制器跟踪所设定期望阀位值。

(1)给定阶跃信号的输出试验，主要考验系统的瞬态性能，给定输出为50%的阀位开度期望信号试验结果如图10所示。

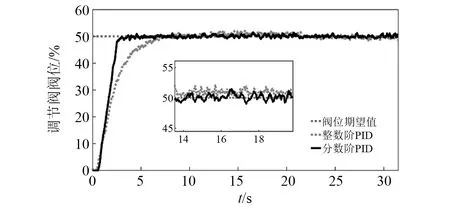
图10 两种算法在50%开度下的阶跃响应信号Fig.10 Step response signals of two algorithms at 50% opening

根据图10，在瞬态响应方面，整数阶PID和PIλDμ的超调量几乎都为0，整数阶PID的上升时间tr=3.669 s、过渡时间ts=5.489 s，PIλDμ的上升时间为tr=1.603 s、过渡时间ts=2.503 s，可见PIλDμ控制器的瞬态性能优于整数阶PID控制器，而在稳态方面，相比于整数阶PID，PIλDμ控制器使系统稳态误差更小、控制精度更高。

(2)给定正弦波的输出试验，主要考验控制器的动态性能，试验中选择阀位跟踪信号为y=30sin(0.4t)+50。试验结果图如图11所示。

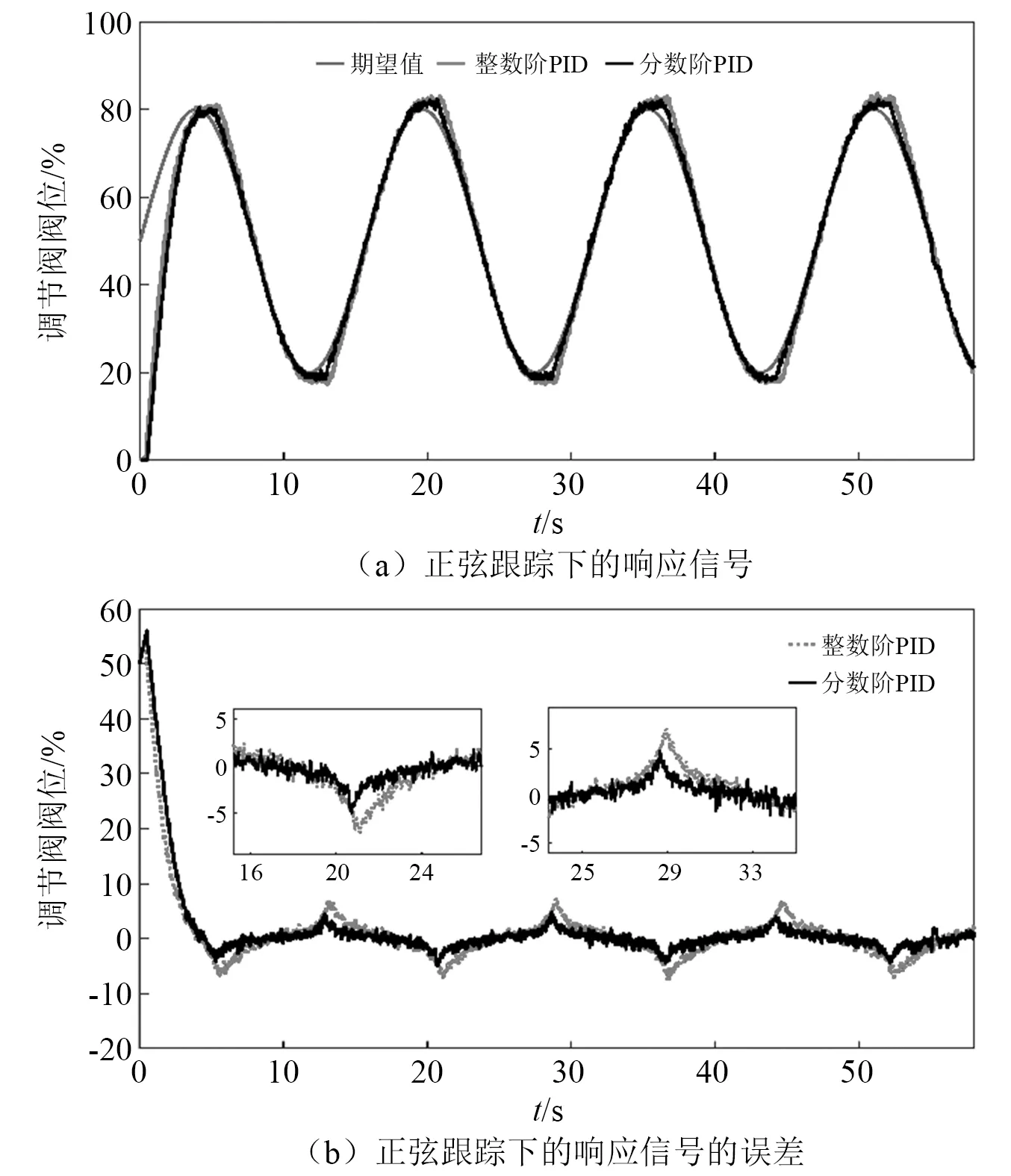
图11 两种算法的正弦试验跟踪曲线及跟踪误差Fig.11 Tracking curve and tracking error of two algorithms in sinusoidal experiment

根据正弦跟踪曲线图中几乎看不出整数阶PID和PIλDμ的控制效果区别，都可以较好的跟踪给定信号，但在误差曲线图中可以看出PIλDμ控制下的正弦跟踪误差更小，因此PIλDμ控制效果优于整数阶PID。

(3)给方波输出试验,主要测试控制器的快速性能和跟踪突变信号能力。设定阀位期望值输出为30%-75%-30%，并重复三～四次。试验结果如图12所示。

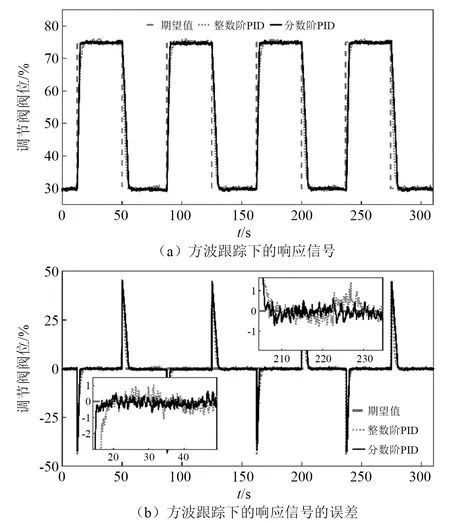
图12 两种算法的方波试验跟踪曲线及跟踪误差Fig.12 Square wave experimental tracking curve and tracking error of two algorithms

由图12可以看出，当给定信号正向或反向突变时，PIλDμ控制下的系统可以更快的几乎无超调的跟踪给定信号，且跟踪误差更小，显然PIλDμ控制器具有更好的动态性能。

同时，为进一步评估两种方法的性能，引入平均绝对误差(mean absolute error,MAE)和平均绝对百分比误差(mean absolute percentage error,MAPE)进一步比较说明，定义如下

(32)

(33)

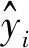
根据表3中指标对比，表明PIλDμ控制器对气动调节阀阀位控制具有更小的平均绝对误差和平均绝对百分比误差，对调节阀的控制精度优于整数阶PID控制器。

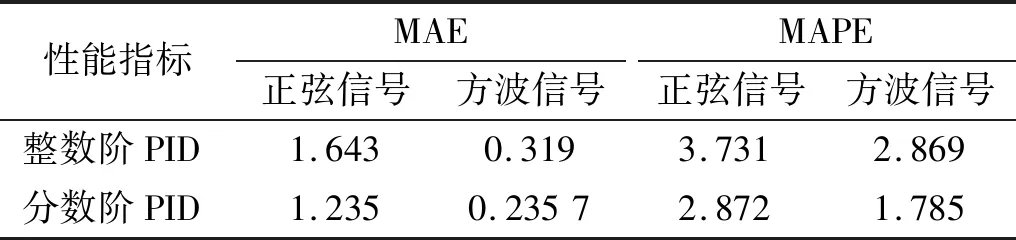
表3 整数阶PID与分数阶PID的性能指标对比Tab.3 Performance comparison between integer order PID and fractional order PID %

7 结 论

本文根据气动调节阀的特点建立了气动调节阀数学模型，在此基础上提出了基于分数阶PID的气动调节阀阀位控制方法。针对PIλDμ控制器参数整定范围广、复杂性高等问题，提出一种改进量子粒子群算法优化PIλDμ控制器参数，通过引入混沌映射增加粒子初始化时种群多样性，引入非均匀高斯变异增强粒子在优化时种群多样性，将改进后算法用于调节阀模型辨识，并由仿真证明了所提方法具有良好效果；最后开展气动调节阀阀位跟踪控制试验，通过上位机LabVIEW图形化编程软件分别编写两种算法的控制程序，并根据试验验证了PIλDμ控制器在气动调节阀阀位控制系统中的适应性和有效性，通过试验对比，PIλDμ相较于整数阶PID具有更优的动态性能，为调节阀阀位的控制提供了一种可靠的方法。