考虑连接部刚度的调焦机构组件动力学特性分析
2022-12-01李永昆王建永张绪国张春瑞
张 春,李永昆,魏 鑫,王建永,张绪国,张春瑞
(1.北京空间机电研究所,北京 100190;2.北京市航空智能遥感装备工程技术研究中心,北京 100190)
调焦机构作为光学遥感器的重要组件,可以校正因环境(振动、压力、温度等)条件变化导致的光学遥感器像面位置产生的偏离,保证遥感器在复杂环境下的成像质量。这就需要研究调焦机构的动力学特性,保证调焦机构在冲击、振动环境下的定位精度。目前,对调焦机构的研究大多针对机构形式设计与验证方面[1-3],而对机构的动力学特性研究内容较少,王永宪等[4]通过理论计算得到了空间遥感器调焦机构组件的低阶固有频率和对应的主振型,并利用锤击法对调焦机构组件进行了模态测试,验证了调焦机构组件的有限元模型准确性,对空间遥感器调焦机构组件试验模态与计算模态进行了对比,说明空间遥感器调焦机构组件计算模态与试验模态具有比较好的相关性。程鹏辉等[5]以某型空间相机调焦机构平台作为研究对象,基于Hertz接触理论获取动力学参数,将调焦平台中滚珠丝杠和联轴器的刚度等效至导轨结合部上,并提出了关系表达式和修正参数,建立了含串联弹簧阻尼单元的调焦平台的有限元模型,通过以联轴器为变量的对比实验获取修正参数,完成了空间相机调焦平台的动力学仿真分析。张巍等[6]以滚珠直线导轨副为研究对象,基于齐次变换矩阵建立了滚珠直线导轨副的接触刚度模型,研究了预紧力和接触角变化对直线滚动导轨刚度的影响规律。
本文以某型航空相机调焦机构组件为研究对象,基于弹性力学中的赫兹接触理论,计算直线滚动导轨的刚度、滚珠丝杠螺母副轴向刚度,分析预紧力与连接部刚度大小的关系,把刚度值嵌入到Bushing连接中,基于Ansys Workbench软件建立考虑连接部刚度的调焦机构组件的动力学模型,分析计算不同预紧力作用下,连接部刚度对调焦机构组件的动态特性的影响,实际应用时匹配合理的预紧力使调焦机构组件中三镜的动力学响应满足要求,确保航空相机在复杂机载振动环境的成像质量。
1 调焦机构组成
调焦机构组件的结构组成如图1所示,其中三镜与三镜框之间通过胶斑[7]黏结固定,三镜框通过螺钉与三镜连接板固连,三镜连接板通过螺钉与螺母固连。步进电机通过联轴器带动丝杠转动,再通过丝杠螺母带动三镜连接板来实现三镜的直线运动。组件的运动简图如图2所示,滚珠丝杠的支承方式为一端固定一端游动,固定端采用配对的角接触球轴承支撑,游动端使用单个深沟球轴承支撑。为了提高各结合部的刚度、消除滚珠丝杠的回程误差,调焦机构组件安装时对丝杠螺母副、滚动导轨副和支撑轴承组进行了预紧。

图1 调焦机构组件Fig.1 Focusing mechanism component
调焦机构组件连接部主要包括导轨滑块-三镜连接板、三镜连接板-三镜框、左轴承座-机架以及右轴承座-机架之间的固定连接部;滚动连接部包括滚珠丝杠螺母副、直线滚动导轨副和配对支撑轴承的连接部。对于固定连接,进行固连处理,忽略接触刚度,对于滚动连接部,均为滚珠与滚道的接触,基于Hertz接触理论计算滚动连接部刚度。
2 连接部刚度计算
2.1 滚珠丝杆螺母副刚度计算
滚珠丝杠螺母副的轴向刚度Kx为与滚珠丝杠副相关联的零部件刚度的串联总和[8],其刚度模型如图2(a)所示。
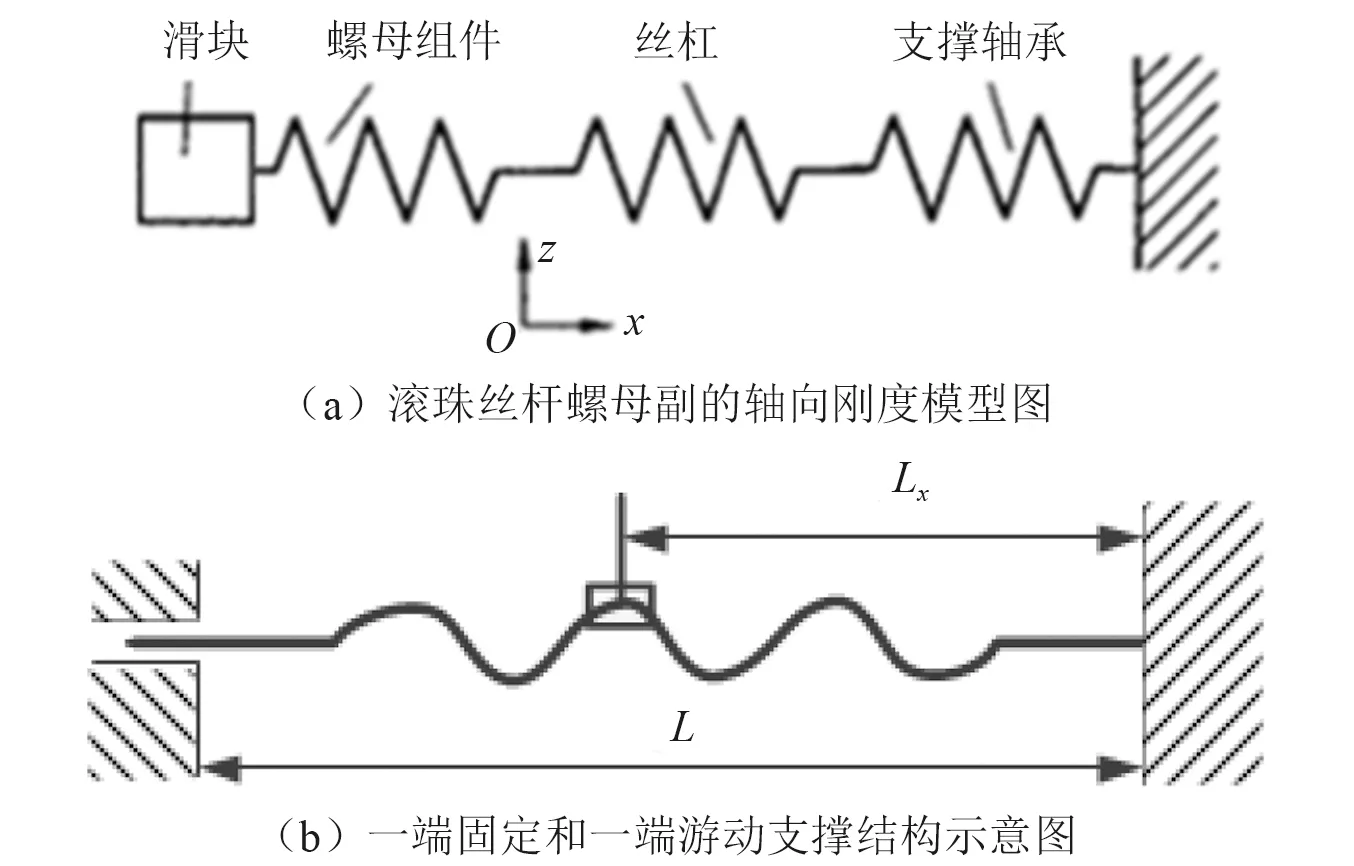
图2 滚珠丝杆螺母副简化图Fig.2 Simplified diagram of ballscrew assembly
由图2(a)可知,滚珠丝杆螺母副的轴向刚度可表示为
(1)
式中:KS为丝杠轴向刚度;KN为螺母组件轴向刚度;KB为支撑轴承轴向刚度。
2.1.1 丝杠刚度的计算
随丝杠支承方式的不同,丝杠轴向刚度的计算存在着差异,如图2(b)所示,本文只讨论一端固定支承和另一端游动的结构方式。
由材料力学[9]得到丝杠的轴向刚度为
(2)
式中:d为丝杠的螺纹底径,mm;Lx为载荷作用点至左端轴承的距离,mm;E为丝杠材料的纵向弹性模量,N/mm2。
当螺母在丝杠最右端位置时,Lx取最大L,KS丝杠轴向刚度KS的值为最小,即
以最小刚度KSmin作为丝杠的轴向刚度值,滚珠丝杠的参数和计算的轴向刚度如表1所示。

表1 滚珠丝杠参数和刚度Tab.1 Parameters and stiffness of the ballscrew
2.1.2 螺母组件轴向刚度:
如图3所示,滚珠丝杠副主要由螺母、滚珠和丝杠螺母组成,丝杠与滚珠和螺母滚道与滚珠的接触满足Hertz接触理论的4个条件[10],滚珠丝杠螺母副采用预压的方式进行预紧,预紧力为Fa。
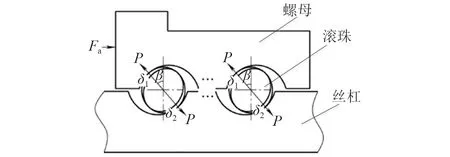
图3 滚珠丝杠和螺母受力简图Fig.3 Force diagram of ballscrew and nut
图3中:P为滚珠对螺母滚到及滚珠对丝杠滚道的法向作用力;β为压力角;δ1和δ2分别为接触变形,则螺母轴向受力平衡方程
Fa-P·Z·sinβcosφ=0
(3)
式中:Z为承载滚珠数目;φ为丝杠的螺旋升角。
根据文献[11]中螺母组件的刚度计算公式,丝杠螺母副的结构参数和计算的刚度如表2所示。

表2 丝杠螺母副参数和刚度Tab.2 Parameters and stiffness of the screw assembly
2.1.3 支撑轴承刚度计算
调焦机构组件丝杠固定端使用配对角接触轴承,预紧力为Fa,配对角接触轴承受力分析如图4所示。
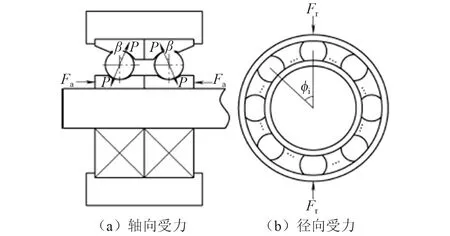
图4 配对角接触轴承受力简图Fig.4 Force diagram of paired angular contact bearing
图4中:β为接触角;P为接触压力;Z为滚珠数目;δ1外圈滚道与滚珠的接触变形;δ2为内圈滚道与滚珠的接触变形,则水平方向轴承的受力平衡方程
Fa-Z·P·sinβ=0
(4)
根据朱坚民等研究中支撑轴承的刚度计算公式,配对角接触轴承的结构参数如表3所示,计算的轴向刚度KB=17.558 N/μm,径向刚度Kτ=61.121 N/μm。

表3 配对角接触轴承参数Tab.3 Parameters of paired angular contact bearing
所以,由以上计算数据代入式(1),计算滚珠丝杠螺母副的轴向刚度
所以,KX=14.528 N/μm。
2.2 直线滚动导轨刚度计算
如图5所示,直线滚动导轨连接部共有4排滚珠。图5中:Z为滚珠总数;β为接触角;F为外部载荷;FU为上排单个滚珠对导轨和滑块滚道的法向力;FL为下排单个滚珠对导轨和滑块滚道的法向力。

图5 滚动导轨受力简图Fig.5 Force diagram of rolling guide
根据朱坚民等研究中直线滚动导轨刚度的计算公式,直线滚动导轨的基本参数如表4所示,计算所得垂向刚度KN=26.483 N/μm,径向刚度Kτ=54.234 6 N/μm。

表4 直线滚动导轨基本参数和刚度Tab.4 Parameters and stiffness of linear rolling guide
2.3 预紧力对连接部刚度的影响
根据2.1节可知,由于丝杠选定后,丝杠的底径和长度就确定了,因此KS大小不变了。同理,螺母组件的轴向刚度KN大小不变。滚珠丝杠螺母副的刚度只与支撑配对轴承的预紧力Fa的大小有关。由2.2节滚动导轨刚度计算过程可知,给定滚动导轨不同预紧力Fa,可得到导轨对应的刚度值,通过计算得到连接部刚度随预紧力变化如图6所示。
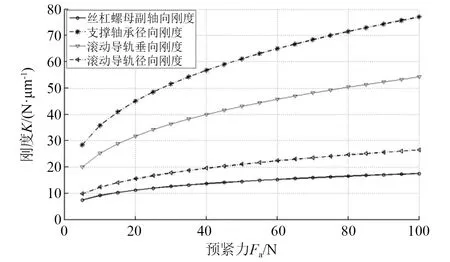
图6 预紧力对连接部刚度的影响Fig.6 Influence of the preload on the joint stiffness
3 调焦机构组件动力学模型的建立
3.1 调焦机构组件实体模型的建立
3.1.1 几何模型简化
首先在Creo4.0软件中建立三维模型,然后保存成后缀名为.x_t文件,将文件导入Workbench的Design Modeler模块中,在不影响结构动态特性的前提下,忽略结构的倒角、圆角等,最后得到其实体模型如图7(a)所示。
3.1.2 材料及物理性能
在Workbench中需要对调焦机构组件的各零件材料属性进行设置,调焦机构组件各零件材料的物理性能和力学性能参数如表5所示。
3.2 定义约束关系和网格划分
根据图1组件的结构组成,三镜、三镜框和三镜连接板之间的连接关系全部设置成固连(黏结:Bonded),三镜连接板与滑块之间采用Bonded连接,支撑轴承与轴承座之间采用Bonded连接,支架与轴承座、电机部件和码盘部件之间采用Bonded连接。
而导轨与滑块为直线运动副、丝杠与螺母为螺旋运动副和丝杠与支撑轴承为转动副,这些有相对运动的零件之间的约束关系统一用Bushing连接来模拟,Bushing连接是一种特殊的连接,是一种通用的运动副连接形式,通过一种数学模型和软件设置来模拟两零件间的弹性阻尼连接[12],由刚度矩阵和阻尼矩阵组成,其中刚度矩阵如式(5)所示。
(5)
式中:Kx,Ky,Kz分别为3个方向的位移刚度;Kxx,Kyy,Kzz分别为3个方向的转动刚度。
通过给定刚度矩阵中的K值,来模拟连接部的实际刚度值,而连接部的阻尼都很小,忽略不计[13],从而仿真计算考虑连接部刚度值时,调焦机构组件的动力学特性。最后通过Workbench中运动副的设置,得到主要零、部件之间的约束关系设置后的约束关系如图7(c)和表6所示。
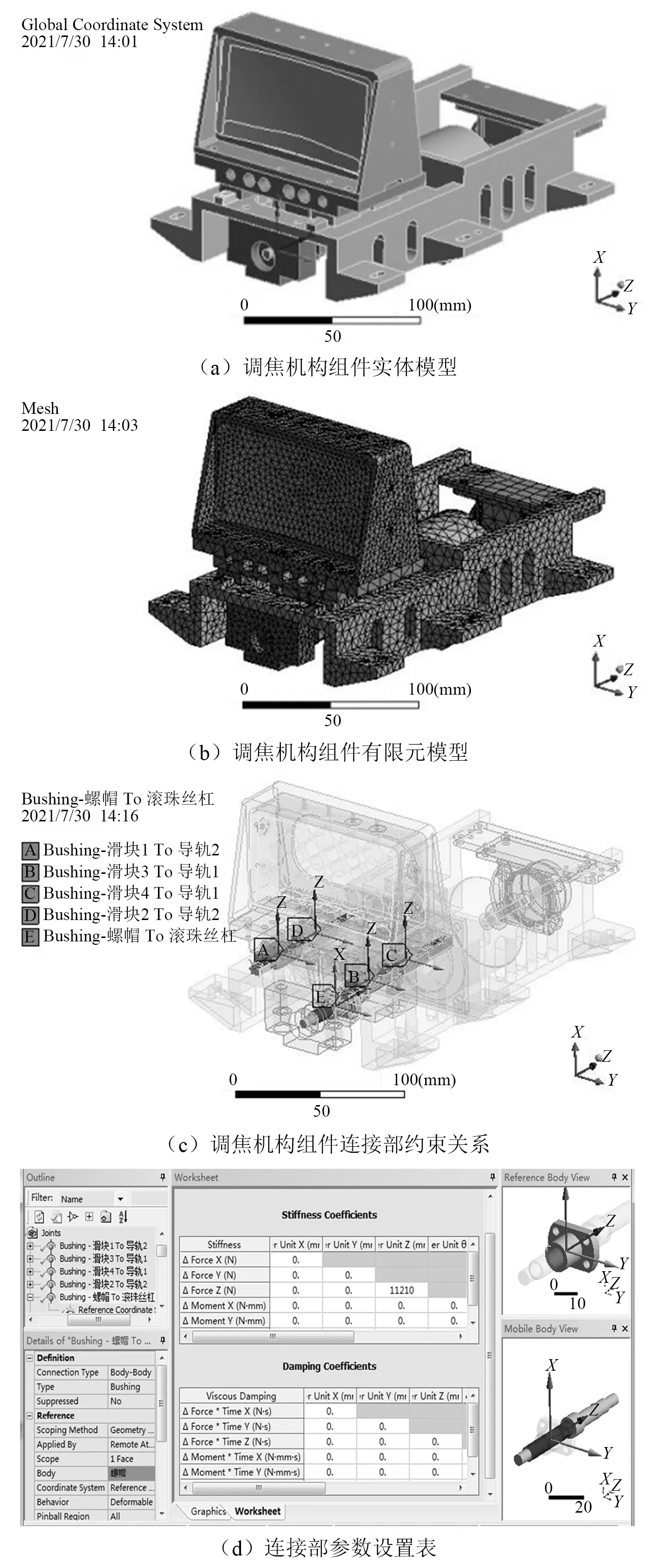
图7 调焦机构组件模型和约束关系Fig.7 Contact relationship and model of the focusing mechanism component
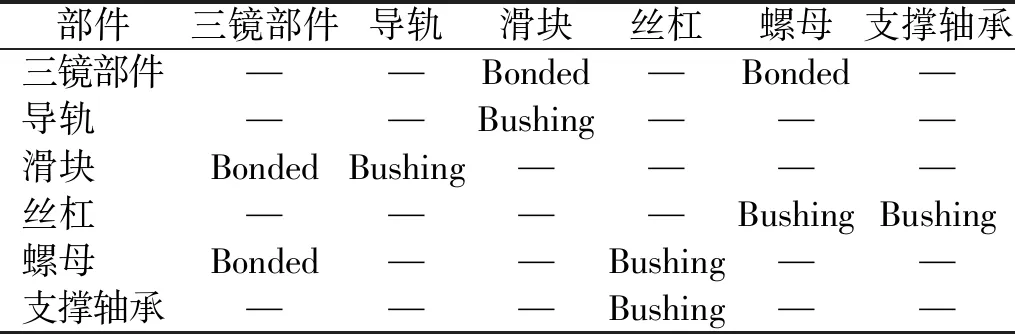
表6 主要部件之间的约束关系Tab.6 Relations of the main parts
3.3 边界条件和仿真参数设置
为了更好地反映调焦机构组件的动力学特性,仿真计算模型的边界条件必须与实际的工况一致。组件工作时,整个组件通过支架的6个腰形孔与大地固连,则采用支架全约束来模拟组件的边界条件。
为研究连接部刚度对调焦机构组件动力学特性的影响,连接部位的刚度情况分如下两种情况进行设置:①不考虑连接部刚度值(刚性连接),即通过定义3.2节中刚度矩阵的刚度值为无穷大,来模拟刚性连接;②考虑连接部刚度值,即把计算得到了各连接部刚度值写入到Bushing连接的刚度矩阵中,来计算考虑连接部刚度时调焦机构组件的动态特性。并可通过改变刚度值进行仿真计算,比较不同刚度值对动态特性的影响,从而匹配连接部合理的预紧力,提高调焦机构组件的固有频率,降低组件中三镜的动力学响应,以适应机载随机振动环境。
4 调焦机构组件的动力学分析
4.1 调焦机构组件的模态分析
4.1.1 模态分析
模态分析用来确定组件的固有频率和振型,为调焦机构组件的动力学分析做准备,通过3.3节中的刚性处理、设置,经过仿真计算,提取前4阶模态,如表7所示,振型如图8(a)所示。通过3.2节中的刚度值设置,取滚珠丝杠螺母副的轴向刚度为11.21 N/μm(轻预紧),滚动导轨的垂向刚度为38.22 N/μm,径向刚度为18.66 N/μm(轻预紧),经过仿真计算,得到考虑连接部刚度时调焦机构组件的固有频率如表7所示,振型如图8(b)所示。
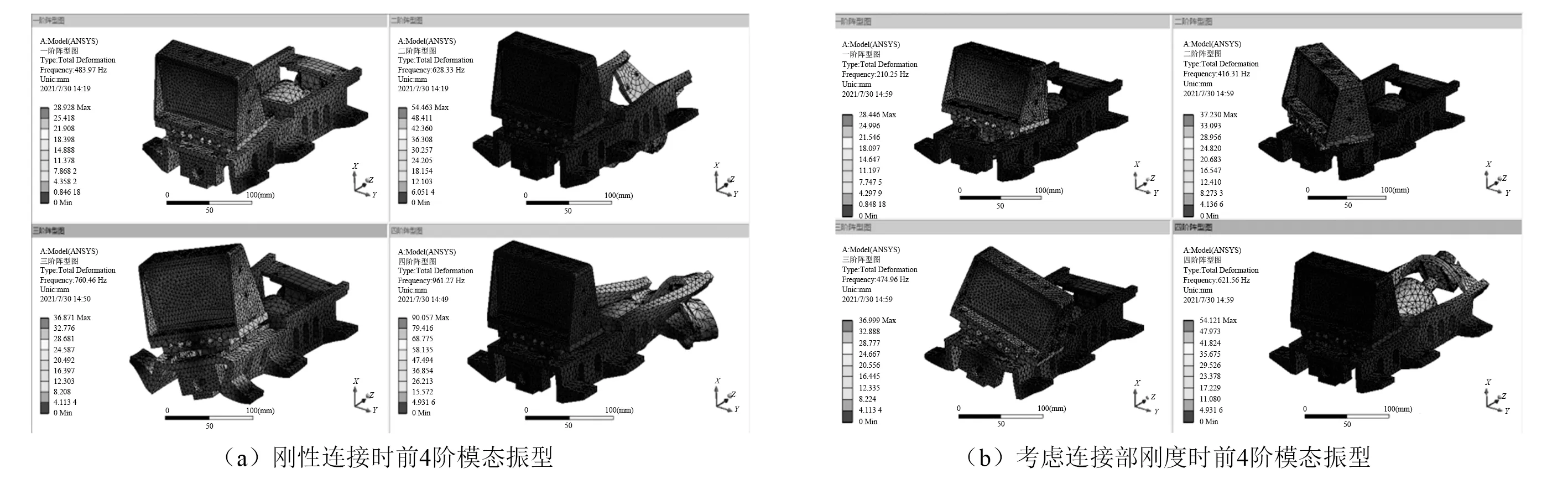
图8 模态振型图Fig.8 Modal shape diagram

表7 模态分析结果Tab.7 Modal analysis results
对比表7可知,连接部刚度是影响调焦机构组件动力学性能的重要因素,特别是对于第1阶固有频率特性计算,影响更为明显,仿真计算时必须考虑连接部的刚度值,不能简单地做刚性连接处理,因此,研究含连接部刚度的调焦机构组件力学模型,对调焦机构组件的动态特性分析与设计有重要意义。
4.1.2 不同刚度值对系统动态特性影响
由2.3节可知,通过匹配不同的预紧力,可以得到不同的刚度值,从而分析不同预紧力对组件系统动态特性影响。保持其他参数不变,改变滚珠丝杠螺母副的轴向刚度,并通过仿真计算,得到不同刚度对应的调焦机构组件的固有频率,在滚珠丝杠螺母副连接部刚度变化的过程中,调焦机构组件的2~6阶频率保持不变,变化的是第1阶频率,第1阶固有频率随连接部刚度的变化如图9(a)所示,第1阶固有频率随着螺母副轴向刚度的增大而增加,并且增加的速度逐渐降低。
保持其他参数不变,按照直线滚动导轨垂向刚度和径向刚度原有的比例,改变滚动导轨的刚度,并通过仿真计算,得到不同刚度对应的调焦机构组件的固有频率,如图9(b)所示,在滚动导轨连接部刚度变化的过程中,调焦机构组件的4阶频率保持不变,变化的是第1~3、第5~6阶固有频率,第1~3、第5~6阶固有频率随着滚动导轨副结合部刚度的增大而增加,并且增加的速度逐渐降低。
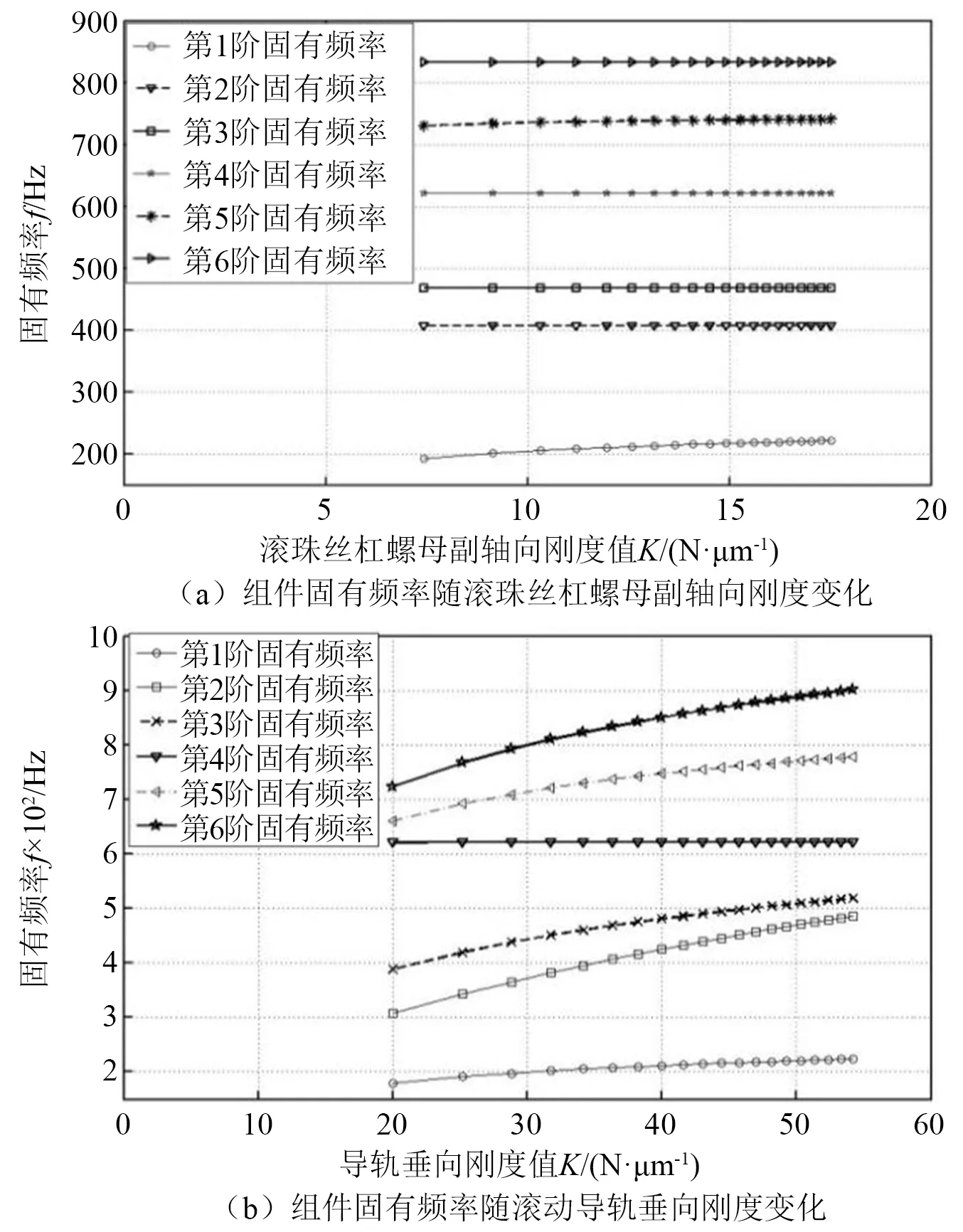
图9 刚度对调焦机构组件固有频率的影响Fig.9 Influences of stiffness on the focusing mechanism component
4.2 连接部刚度对组件的随机振动影响分析
如图1所示,调焦机构组件实际工作时三镜沿着导轨运动到规定的位置锁定,组件承受的随机振动激励曲线如图10所示。
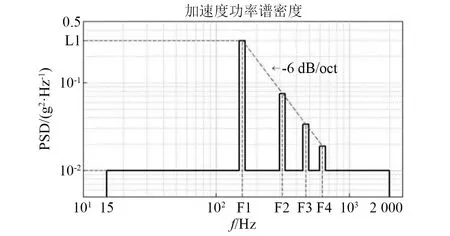
1.F1=156.7 Hz,F2=2F1,F3=3F1,F4=4F1;2.L1=0.3 g2/Hz;3.振动带宽等于围绕每个频率F1~F4的±5%。图10 随机振动功率谱密度曲线Fig.10 Random vibration PSD
为保证调焦机构组件锁定条件下,承受机载振动时三镜几何中心点位置的振动位移响应RMS≤0.05 mm,根据匹配滚珠丝杠螺母副和滚动导轨副不同的刚度值,通过仿真计算并提取得到三镜几何中心点的位移功密度曲线如图11所示。图11中:各曲线与横坐标围成面积的平方根就是中心点位置的随机振动位移响应RMS值[14];三镜几何中心点位置的振动位移响应满足RMS值小于等于0.05 mm指标要求曲线有两条,保守取0.023 mm的那条曲线,此时需匹配各连接部刚度值和预紧力如表8所示。
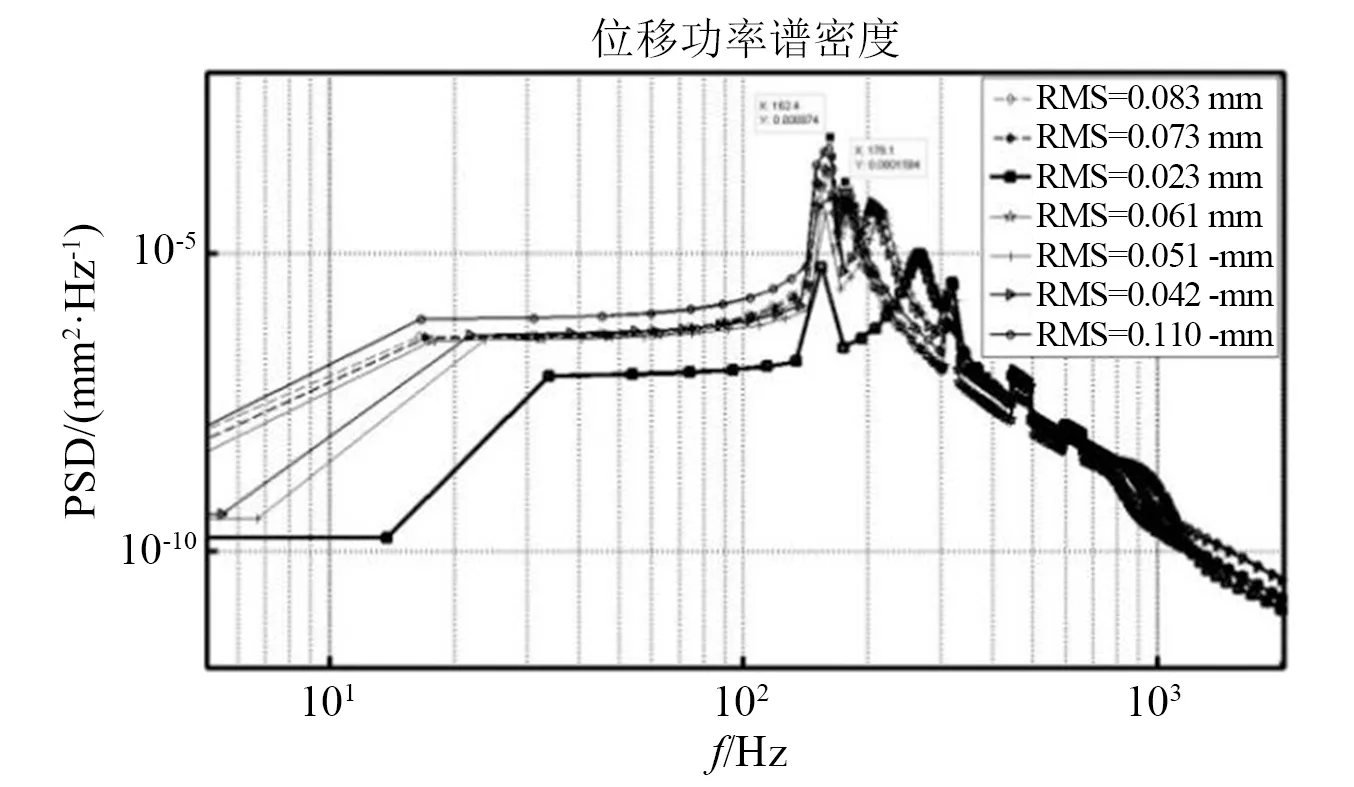
图11 不同刚度值对应的三镜中心位置的位移功率谱密度Fig.11 The displacement PSD of the three mirror center position with different stiffness values
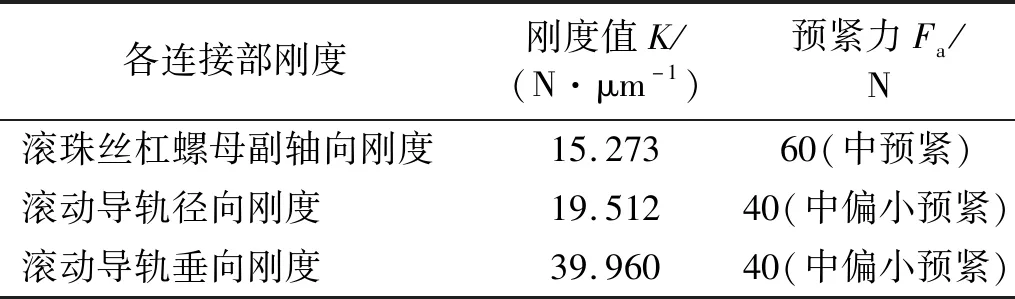
表8 连接部刚度值和预紧力值Tab.8 Stiffness and preload of joints
由表8且结合第2章连接部刚度计算过程可知实际使用中选用支撑配对轴承的预紧力为60 N,为中预紧量,滚动导轨预紧力为40 N,为中等偏小预紧量。仿真计算对应组件的1阶固有频率为312.36 Hz,避开激励的1频点156.7 Hz,提高了组件的动力学特性,降低了三镜的动力学响应,调焦机构组件的应变云图如图12所示。由图12可知,组件最大的随机振动位移响应为0.034 mm,发生在三镜顶端,三镜中心位置附近的振动位移响应为0.025 8 mm,与图11中的曲线保持一致。
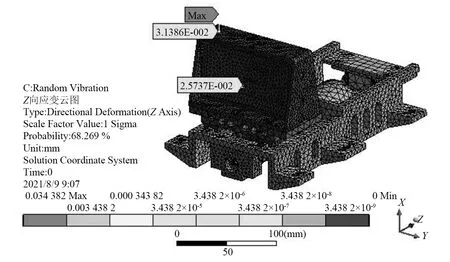
图12 调焦机构组件的应变云图Fig.12 The strain of the focusing mechanism component
5 结 论
为研究连接部刚度对调焦机构组件动力学特性的影响,以某调焦机构组件为研究对象,采用赫兹接触理论计算得到组件各连接部的刚度值,把刚度值嵌入到Bushing连接的刚度矩阵中,基于Ansys Workbench软件,建立了考虑连接部刚度的调焦机构组件的动力学模型,完成了组件模态分析和随机振动分析,详细地研究了刚度值对组件动力学特性的影响,结论如下:
(1)连接部刚度是影响调焦机构组件固有频率的重要因素,特别是对于第1阶固有频率影响更为明显,组件建模仿真时必须考虑连接部的刚度值,不能将连接部简单地做刚性连接处理,应考虑连接部刚度对调焦机构组件的动态特性影响。
(2)滚珠丝杠螺母副的轴向刚度影响组件的第1阶固有频率,且第1阶固有频率随着螺母副轴向刚度的增大而增加,并且增加的速度逐渐降低。滚动导轨垂向刚度和径向刚度影响组件的第1~3、第5~6阶固有频率,且第1~3、第5~6阶固有频率随着滚动导轨副结合部刚度的增大而增加,并且增加的速度逐渐降低。
(3)为保证调焦机构组件锁定条件下,承受机载振动时三镜中心点位置的振动位移响应满足小于等于0.05 mm的指标要求,通过仿真计算可知实际使用中滚珠丝杠副的预紧力为60 N,为中预紧量,滚动导轨副预紧力为40 N,为中等偏小预紧量。此时组件的1阶固有频率为312.36 Hz,避开随机激励的1频点156.7 Hz,提高了组件的整体刚度,避开了共振频率点。组件最大的随机振动位移响应为0.034 mm,降低了三镜的随机振动位移响应,增强了调焦机构组件的抗机载振动环境的能力。
