中介轴承复合故障动力学建模与振动特征分析
2022-12-01艾辛平刘丽丽张凤玲
田 晶,艾辛平,刘丽丽,张凤玲,王 志
(沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室,沈阳 110136)
中介轴承是双/三转子航空发动机转子系统的关键部件。中介轴承工作在高温、高压、高转速和重载的恶劣工况下,极易发生机械故障。中介轴承一旦出现故障,将会起整台发动机发生事故。建立准确的中介轴承动力学模型,分析中介轴承故障特征,对发展中介轴承故障诊断具有重要意义。
Walters[1]首次开展动力学建模尝试,随后国内外专家学者针对滚动轴承动力学建模开展了大量研究。Gupta[2-3]建立了对轴承各部件运动及受力状态进行描述的动力学模型。Patel等[4-5]提出了一种深沟球轴承6自由度动力学模型,采用脉冲序列和延迟脉冲序列组合的形式对恒定载荷下单点故障和多点故障进行仿真分析。Patil等[6]基于非线性接触理论将滚道和滚子之间的接触考虑成一个非线性接触弹簧,提出了一种用于分析局部缺陷的动力学模型。张建军等[7]建立的轴承故障6自由度模型,考虑了由轴承间隙引起的变刚度振动,使用单元谐振器模拟故障轴承元件的高频固有振动。剡昌锋等[8-9]基于非线性Hertz理论,考虑了弹流润滑的影响,建立了深沟球轴承单点故障2自由度模型,深入分析了弹流润滑对滚动体与滚道之间接触刚度的影响。董振振[10]同样以Hertz接触理论为基础,采用脉冲序列对滚动轴承存在的单点故障和复合故障情况进行分析,建立了考虑撞击力的动力学模型。王凯[11]对滚动体经过滚道的全过程进行了有限元分析,在此基础之上建立了相应的4自由度动力学模型。Cao等[12-13]将Gupta的轴承模型与刚性滚动体模型相结合,建立了球轴承转子系统的动力学模型。该模型考虑了转子-轴承-轴承座系统的转子弹性变形,研究了在配合间隙影响下轴承系统的振动特性和稳定性。结果表明配合间隙会引起局部冲击现象。Chen等[14]提出了一种基于Hertz接触理论的振动信号模型,探究了振动信号的变化过程。在滚动轴承动力学建模方法基础上,结合中介轴承的工作特点,学者们也提出了多种中介轴承动力学建模方法。徐可君等[15]建立了一种中介轴承内圈存在单一故障的动力学模型,该模型考虑轴承的径向游隙以及内、外圈的径向载荷。曹宏瑞等[16-17]以Gupta复杂动力学模型为基础,分别研究了高速运转下普通轴承和中介轴承的时变刚度受静载荷和动载荷的影响规律,还针对中介轴承的磨损故障和局部缺陷故障建立了相应的动力学模型,并对这两种故障所带来的振动响应进行了分析。研究表明,基于非线性Hertz接触理论建立的滚动轴承动力学模型能够有效模拟滚动轴承的故障特征,同时相较于其他方式,采用考虑时变位移激励的建模方式可以更加准确的描述带有局部缺陷轴承的实际工作状态。
本文对中介轴承振动故障特性进行分析,结合现有滚动轴承动力学建模方法,提出了一种基于非线性Hertz接触理论的4自由度动力学模型,实现了中介轴承内圈多点故障、外圈多点故障和内外圈多点复合故障的振动特征分析,模型中采用时变位移激励描述滚子的多点局部缺陷的冲击,并通过试验验证了所建模型的有效性与准确性。
1 故障动力学模型建立
1.1 非线性Hertz接触模型
航空发动双转子通常采用内、外圈同向或反向旋转方式工作,中介轴承位于高、低压转子之间,内、外圈随高、低压转子旋转,比普通轴承具有更为复杂的动力学特性。本文以内、外圈反向旋转的情况为例,在非线性Hertz接触理论的基础上,采用时变位移激励对轴承内圈多点故障、外圈多点故障、内外圈复合故障进行模拟,建立4自由度多点故障动力学模型。模型中假设滚动体不发生打滑,内圈缺陷和外圈缺陷的形式相同。中介轴承径向位移图如图1所示。
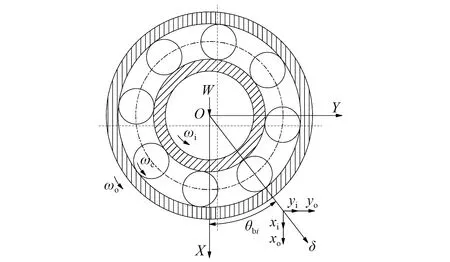
图1 中介轴承径向位移图Fig.1 Radial displacement diagram of inter-shaft bearing
本文采用非线性Hertz接触力-变形关系来计算滚子和接触点之间的弹性趋近量,公式如式(1)所示[18]
Q=Kδn
(1)
式中:K为Hertz接触刚度;δ为径向变形量。对于圆柱滚子轴承n=10/9,K=8.06×104l8/9,其中l为滚子长度。
因为中介轴承的内、外圈均存在振动,所以滚子在内外圈之间总的变形量δ为
δ=(xo-xi)cosθbi+(yo-yi)sinθbi-Cr-Ht
(2)
式中:xo和yo分别为外圈中心沿X轴和Y轴方向上的位移;xi和yi为内圈中心沿X轴和Y轴方向上的位移;θbi为第i个滚子中心与X轴的夹角;Cr为滚子和滚道之间的初始径向间隙;Ht为滚子经过缺陷时产生的时变位移激励。
(3)
(4)
式中:θb0为第1个滚子在初始时刻相对于X轴的夹角;Z为中介轴承滚子个数;ωc,ωi和ωo分别为中介轴的保持架、内圈和外圈的角速度;db为滚子直径;Dm为中介轴承节径;α为中介轴承接触角。
由式(1)可得到第i个滚子的非线性Hertz接触力为
Qi=K[(xo-xi)cosθbi+
(yo-yi)sinθbi-Cr-Ht]10/9
(5)
因此,中介轴承总的非线性Hertz接触力在X方向和Y方向上的分量分别为
(6)
1.2 故障动力学模型
基于非线性Hertz接触理论,建立4自由度中介轴承复合故障的动力学模型如下
(7)
式中:Mi为内圈质量;Mo为外圈质量;Fi内圈所受偏心载荷;Fo为外圈所受偏心载荷;W为轴承所受径向载荷;Ki为 内圈与滚子接触刚度;Ko为外圈与滚子接刚度;Ci为轴承径内圈向间隙;Co为轴承径外圈向间隙;λ为滚子与滚道是否接触的开关量,表达式为
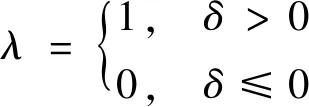
(8)
2 轴承故障时变位移激励
在滚子经过缺陷的整个过程中,位移激励先增大后减小,此过程与半正弦函数相似,所以采用分段函数来描述时变位移激励。图2所示为滚子经过缺陷的过程图,图2中滚子经过缺陷时产生的最大附加位移H如式(9)所示。
(9)
式中:db为滚子直径;b为缺陷宽度。时变位移激励是指滚子在公转过程中,滚子中心在径向方向上位移随时间的变化量。
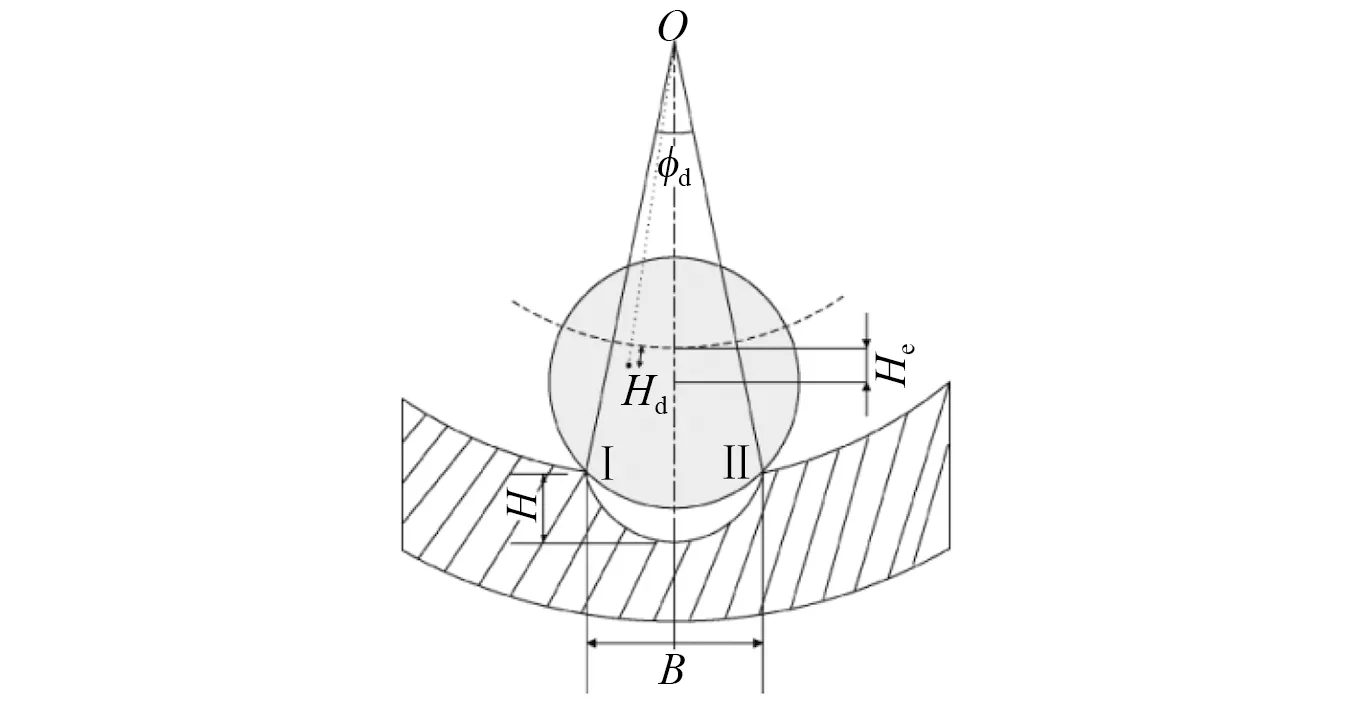
图2 滚子经过缺陷过程图Fig.2 Process of roller through the defect
2.1 内圈多点故障时变位移激励
本文研究内圈同时存在两点缺陷的情况。中介轴承内、外圈反向旋转时滚子和内圈缺陷的位置关系,如图3所示。图3中:ωi,ωo和ωc分别为内圈、外圈和保持架的角速度;σ01为故障的缺陷角度;σ02为另一个故障的缺陷角度,规定逆时针为正方向。
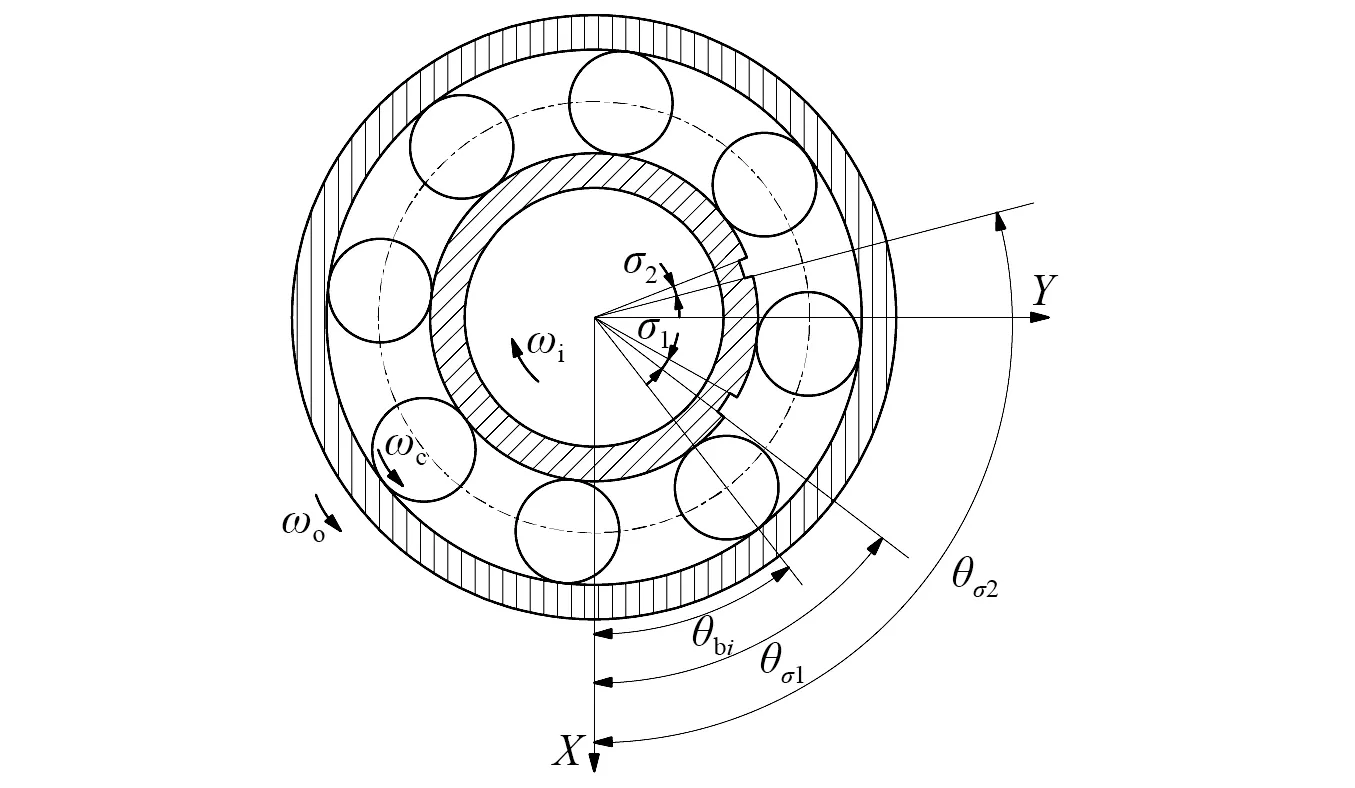
图3 内圈多点故障滚子和缺陷位置关系图Fig.3 Location relation diagram of roller and defect in inner ring with multi-point faults
假设ωo>ωi,根据保持架角速度ωc与内圈和外圈角速度的大小关系,可以判断其保持架角速度ωc的值处于内圈角速度和外圈角速度之间,方向与外圈方向一致。经过时间t,两种故障的位置角度分别为θσ1和θσ2。时变位移激励Hmi可由式(10)表示为
(10)
(11)
式中:mod为求余;H为滚子经过缺陷时产生的最大附加位移;θb0为初始时刻第1个滚子的位置角度;θσ01和θσ02分别为初始时刻两种故障右侧的位置角度。
2.2 外圈多点故障时变位移激励
当中介轴承外圈同时存在两点故障,内、外圈反向旋转时,滚子经过内圈缺陷产生的时变位移激励Hmo如式(12)所示
(12)
(13)
θφ1=ωot+θφ01
(14)
θφ2=ωot+θφ02
(15)
式中:mod为求余;H为最大附加位移;θb0为第1个滚子在初始时刻的位置角;θφ01和θφ02分别为在初始时刻两故障右侧相对X轴的角度。
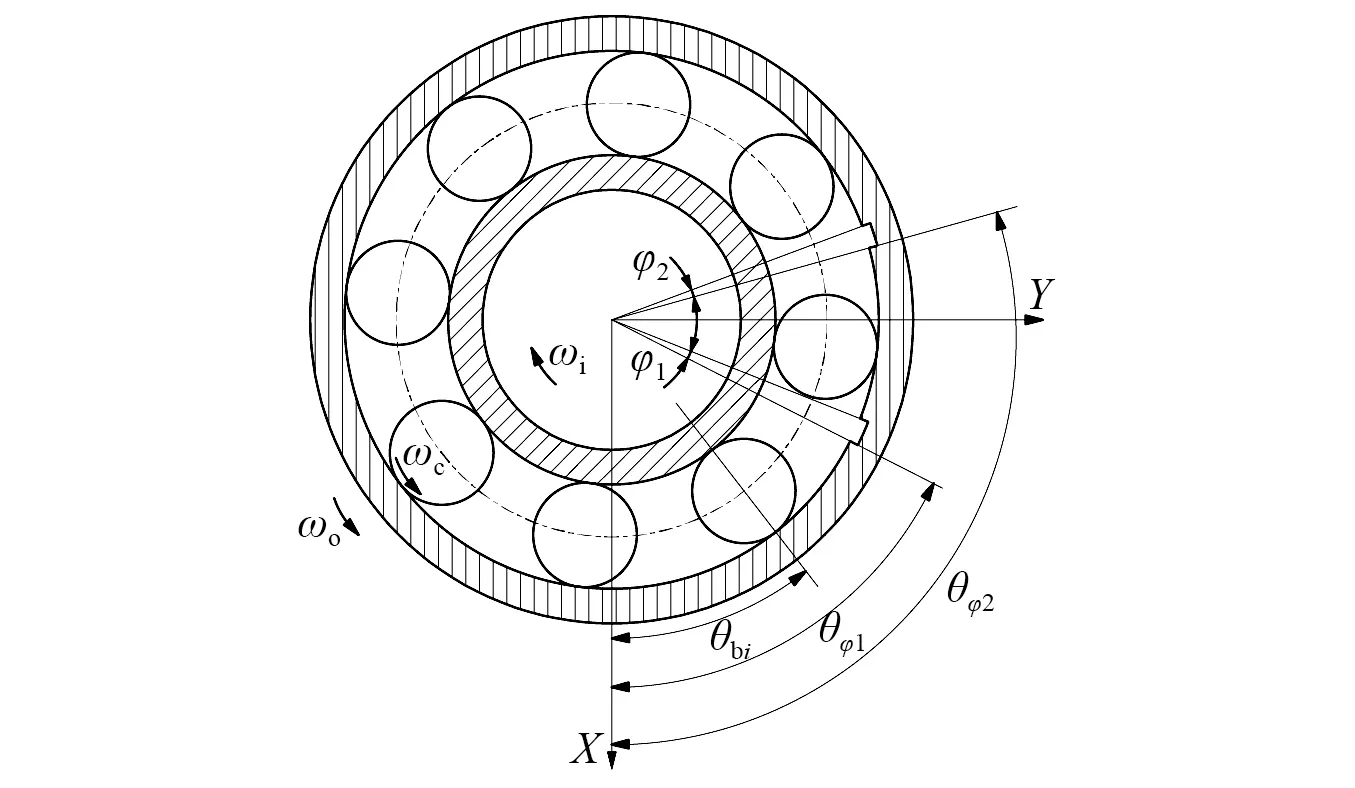
图4 外圈多点故障滚子和缺陷位置关系图Fig.4 Location relation diagram of roller and defect in outer ring with multi-point fault
2.3 内外圈复合故障时变位移激励
当中介轴承内圈存在单点故障,内、外圈反向旋转时,滚子经过内圈缺陷产生的时变位移激励Hti如式(16)、式(17)所示
(16)
(17)
当中介轴承外圈存在单点故障,内、外 圈反向旋转时,滚子经过外圈缺陷产生的时变位移激励Hto如式(18)、式(19)所示
(18)
(19)
基于单点故障的时变位移激励,当设置内、外圈各一个缺陷时,得出滚子在内外圈之间总的变形量δ为
δ=(xo-xi)cosθbi+
(yo-yi)sinθbi-Cr-Hti+o
(20)
式中,Hti+o为中介轴承内、外圈复合故障的时变位移激励。Hti和Hto以及Hti+o之间的关系为Hti+o=Hti+Hto。将其代入式(2)中可对复合故障进行描述。
3 试验验证
3.1 试验设备与轴承参数
中介轴承支承结构主要应用在双转子航空发动机中。中介轴承的外圈连接于高压转子,内圈与低压转子相连,既可以同向旋转又可以反向旋转。根据中介轴承的实际工作状态搭建试验台,如图5所示。

图5 中介轴承试验台Fig.5 Inter-shaft bearing test rig
试验采用西门子公司的LMS SCADAS Recorder SCR202系统采集振动信号,该采集系统具有2个转速通道,8个振动信号采集通道,最大采样频率为102 400 Hz,24位的采样精度,如图6所示。

图6 LMS数据采集仪Fig.6 LMS data acquisition instrument
试验采用6个加速度传感器,型号均为333B30,传感器的采样范围是0~6 400 Hz,本文试验设置的采样频率为4 096 Hz,频率分辨率为0.1 Hz。3个传感器安装在靠近低压电机的轴承座上,灵敏度分别为98.6 mV/g,99 mV/g和97.6 mV/g,如图7(a)所示;其余3个安装于中介轴承的轴承座上,灵敏度分别为99.3 mV/g,98.3 mV/g和100.4 mV/g,如图7(b)所示,用于检测轴承3个方向的振动。
3.2 轴承结构参数
试验采用NSK公司NU202EM型号的圆柱滚子轴承作为试验轴承。轴承参数如表1所示。使用电花火线切割的加工方式,在正常的轴承内、外圈上,加工出纵向贯穿整个滚道的矩形故障,故障的宽度和深度均为1 mm。

图7 加速度传感器布置示意图Fig.7 Acceleration sensor layout schematic

表1 NU202EM轴承参数Tab.1 NU202EM bearing parameters
3.3 振动特征分析
3.3.1 中介轴承内圈多点故障
本文设置内圈转速为200 r/min,外圈转速为1 000 r/min,根据文献[19]的中介轴承故障特征频率公式计算出此转速下中介轴承的故障特征频率理论值,如表2所示,其中反向旋转指内、外圈反向旋转的情况。

表2 内圈多点故障特征频率理论值Tab.2 Theoretical value of characteristic frequency of inner ring multipoint fault
基于本文所建立的模型计算出内圈多点故障的时域波形和包络谱[20],如图8所示。从图8中可以看出,仿真模拟的故障特征频率Fi为132.1 Hz,与表2中理论计算故障特征频率值132 Hz基本一致。图9表示为试验测得的时域波形和包络谱图。对比仿真分析与试验结果可以发现,在时域波形中可以看出中介轴承内圈存在多点故障时,信号具有周期性的脉冲特征。在包络谱中可以看到明显的转频及其倍频、故障特征频及其倍频。由于滚子与缺陷的接触处存在周期性变化,故障信号会出现以故障频率为中心,转频及其倍频为边带的转频调制幅值频率现象。图9中试验测得的故障特征频率为131 Hz,而理论模型仿真分析的故障特征频率为132.1 Hz,对比发现试验数据与理论数值误差小于1%。且转频、倍频及边带频均与模拟的包络谱相同,因而验证了该模型的有效性与准确性。
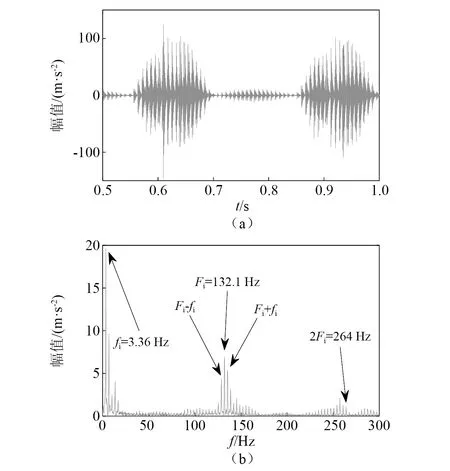
图8 反向旋转时内圈多点故障时域波形和包络谱仿真结果Fig.8 Simulation results of time domain waveform and envelope spectrum of inner ring with multi-point fault in reverse rotation
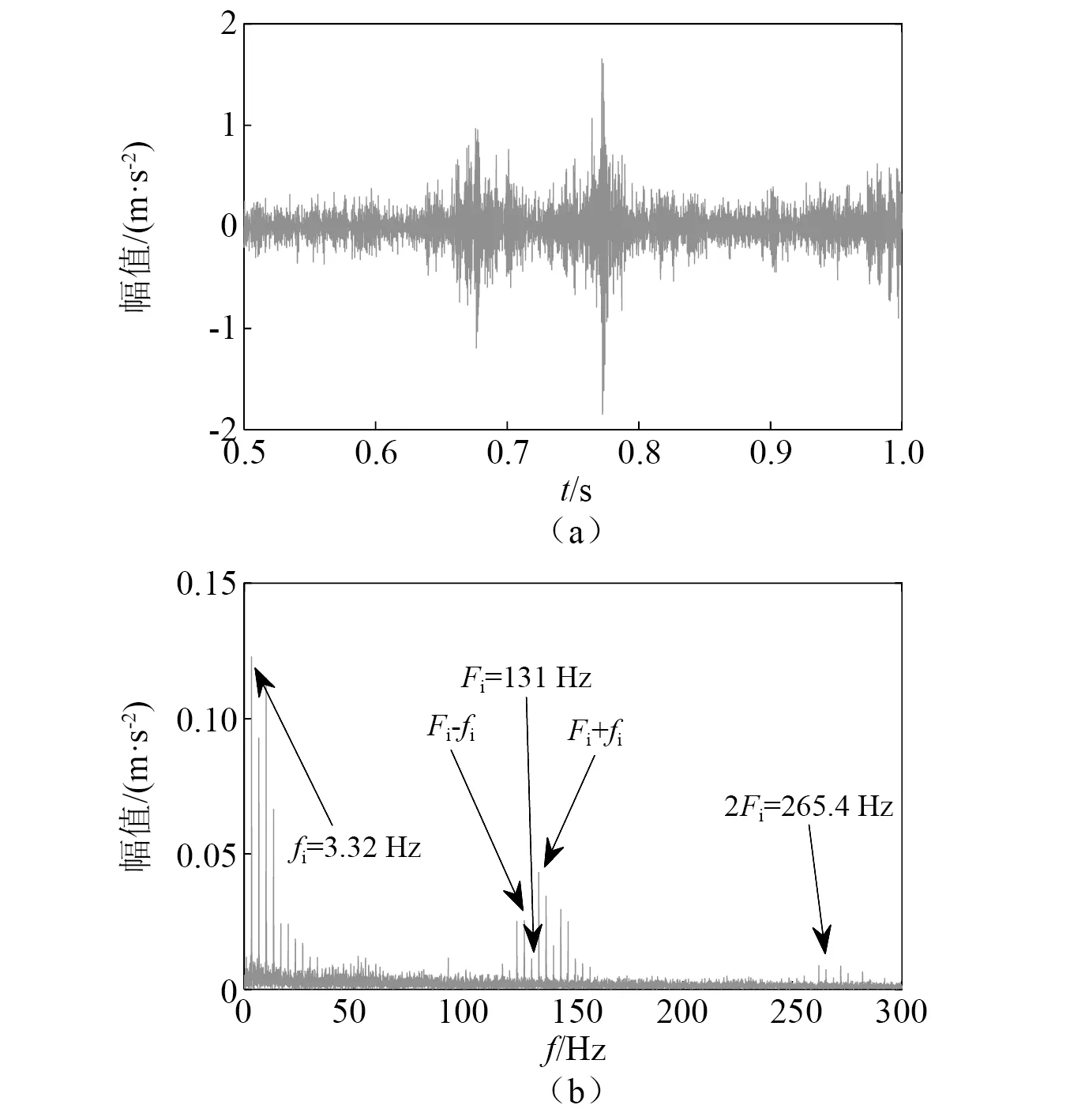
图9 反向旋转时内圈多点故障时域波形和包络谱试验结果Fig.9 Experimental results of time domain waveform and envelope spectrum of inner ring with multi-point fault in reverse rotation
图10为滚子与缺陷的位置关系图,图10为提取的局部时域信号细节图。图10中的脉冲叠加现象是由于内圈含有2个故障,同一个滚子在相隔的时间内和2个故障接触形成脉冲。假设图11中t1时刻的脉冲是由图10中第1个滚子和第1个故障产生的,则t2时刻的脉冲是由第2个滚子和第2个故障形成的,通过内圈和保持架的转速关系,可以计算出这2个脉冲的时间间隔为0.005 79 s。同理,t3与t1时刻的脉冲均是由第1个故障产生,2个脉冲的时间差值为1/132=0.007 58 s。而通过图11可计算t2-t1=0.005 7 s,t3与t1的时间间隔为0.007 6 s,两组数值基本一致,证明了模型的准确性。
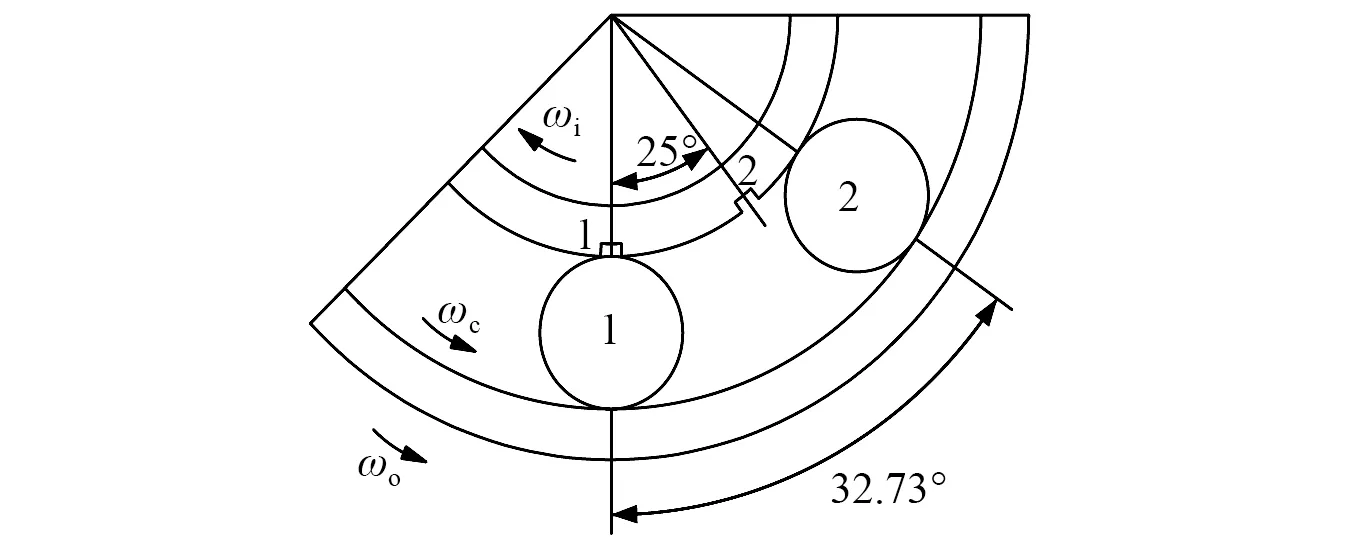
图10 反向旋转内圈多点故障运动分析图Fig.10 Motion analysis diagram of inner ring with multi-point fault reverse rotation
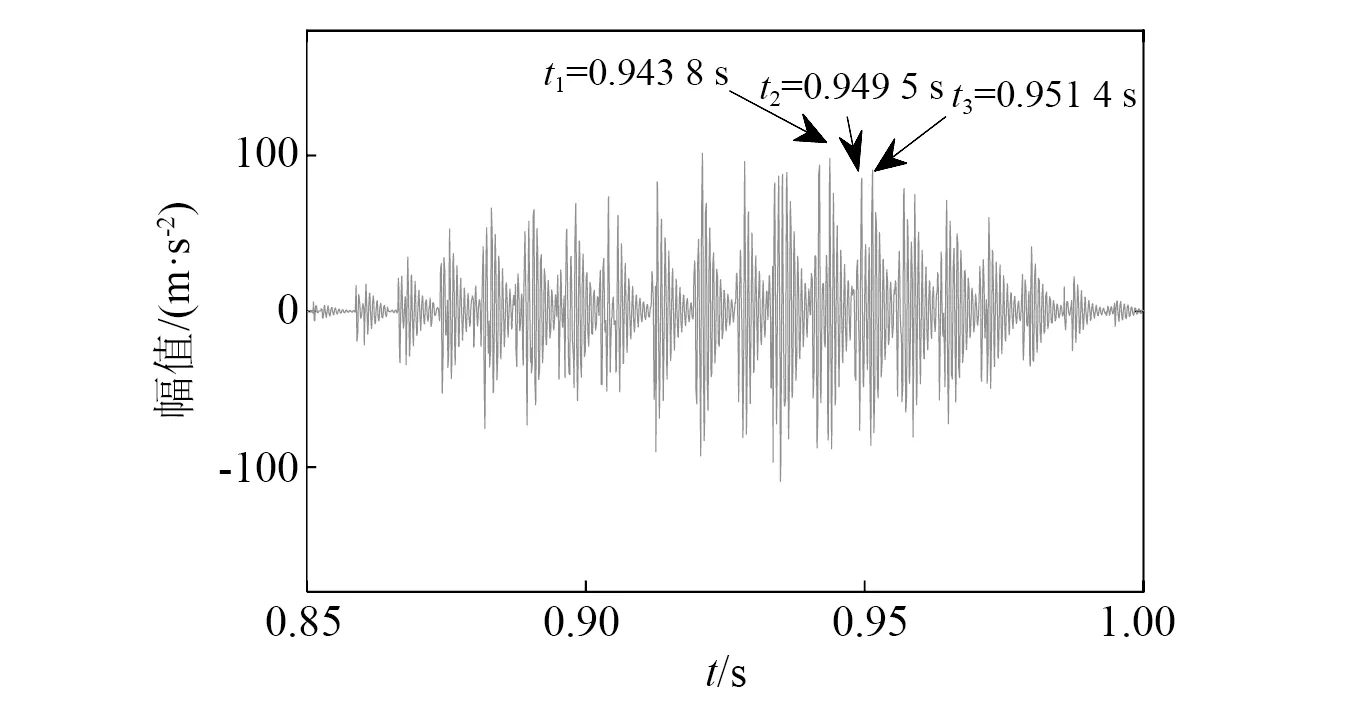
图11 仿真模拟反向旋转内圈多点故障时域波形细节图Fig.11 Simulation results of detailed time domain waveform of inner ring with multi-point fault in reverse rotating
3.3.2 外圈多点故障试验验证
在分析外圈多点故障时,设置内圈转速为800 r/min,外圈转速为200 r/min,此转速下中介轴承的故障特征频率理论值,如表3所示。

表3 外圈多点故障特征频率理论值Tab.3 Theoretical value of characteristic frequency of outer ring multipoint fault
外圈多点故障的仿真模拟的时域波形和包络谱,如图12所示。仿真模拟的故障特征频率Fo为73.2 Hz,表3中的经验公式计算故障特征频率理论值为73.3 Hz,两者计算误差为0.1 Hz。从时域波形中可以看出中介轴承外圈存在多点故障时具有周期性的脉冲特征。同一个故障与不同滚子接触形成的脉冲为故障特征频率的倒数。
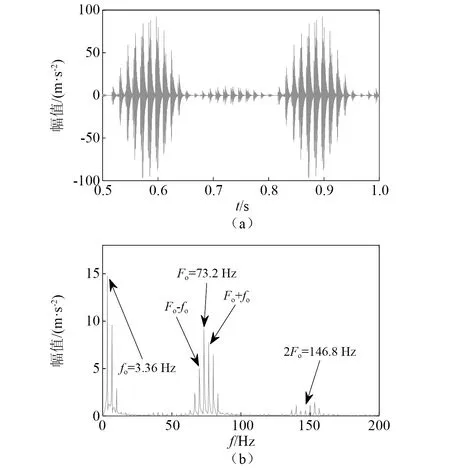
图12 反向旋转时外圈多点故障时域波形和包络谱仿真结果Fig.12 Simulation results of time domain waveform and envelope spectrum of outer ring with multi-point fault in reverse rotation
图13为故障轴承模拟试验获得时域波形和包络谱图。图13中存在周期性的脉冲信号是同样由于滚子受到内、外圈转动及保持架转动频率的调制包络谱中存在的故障频率以及故障频率的边频同样证明该现象的发生。在包络谱中的故障特征频率试验值Fo为73.1 Hz,与理论模型仿真模拟的故障特征频率73.2 Hz同样仅差0.1 Hz,试验结果与理论的故障特征频率值基本一致。证明了数值模型的准确性。

图13 反向旋转时外圈多点故障时域波形和包络谱试验结果Fig.13 Experimental results of time domain waveform and envelope spectrum of outer ring with multi-point fault in reverse rotation
图14为滚子与缺陷的位置关系图。图15为提取的局部时域细节图。与内圈多点故障中滚子的运动相似,根据相对位置关系可计算t2与t1的时间间隔为0.003 22 s,t3与t1的时间间隔为故障特征频率的倒数,即1/73.3=0.013 64 s。而通过图15可提取得t2-t1=0.003 3 s。同理,t3与t1的时间间隔为0.013 7 s,与分析值保持一致。
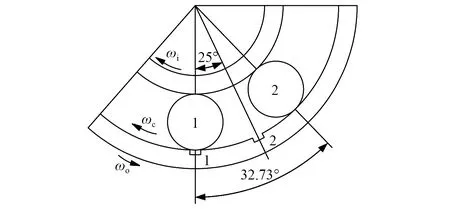
图14 反向旋转外圈多点故障运动分析图Fig.14 Motion analysis diagram of outer ring with multi-point fault reverse rotation
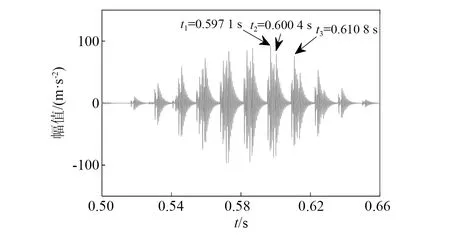
图15 仿真模拟反向旋转外圈多点故障时域波形细节图Fig.15 Simulation results of detailed time domain waveform of outer ring with multi-point fault in reverse rotating
3.3.3 内外圈复合故障试验验证
设置中介轴承内圈转速为300 r/min,外圈转速为1 400 r/min。根据田晶等的研究计算得到中介轴承内、外圈故障频率,如表4所示。

表4 内、外圈复合故障特征频率理论值Tab.4 Theoretical value of characteristic frequency of compound fault inner and outer rings
基于本文所建立的模型计算出内、外圈复合故障的仿真模拟时域波形和包络谱如图16所示。在图16中可以观察到内圈、外圈的故障特征频率。内圈故障特征频率Fi为187.1 Hz,外圈故障特征频率Fo为124.5 Hz,二者与表4中经验公式计算的故障特征频率187.0 Hz和124.7 Hz的误差值小于1%。图17为故障轴承由试验得到的时域波形和包络谱图。时域波形中可以明显的观察到存在两种冲击信号,包络谱中同样包含内圈和外圈各自的转频、故障特征频率和边带频及其二倍频。这说明,内、外圈均有故障时,内、外圈故障相互独立,互不干扰,内外圈复合故障信号为内、外圈单点故障信号的叠加,且受转频调制。在包络谱中试验测得的内圈故障特征频率试验值为188.8 Hz,外圈故障特征频率试验值为125.1 Hz,对比理论模型仿真得到的故障特征频率值187.1 Hz和124.5 Hz,误差同样小于1%。因而验证了该模型的有效性与准确性。
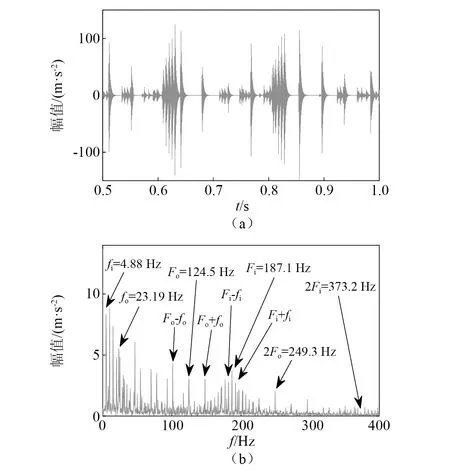
图16 反向旋转时内、外圈复合故障时域波形和包络谱仿真结果Fig.16 Simulation results of time domain waveform and envelope spectrum of compound fault inner and outer rings in reverse rotation
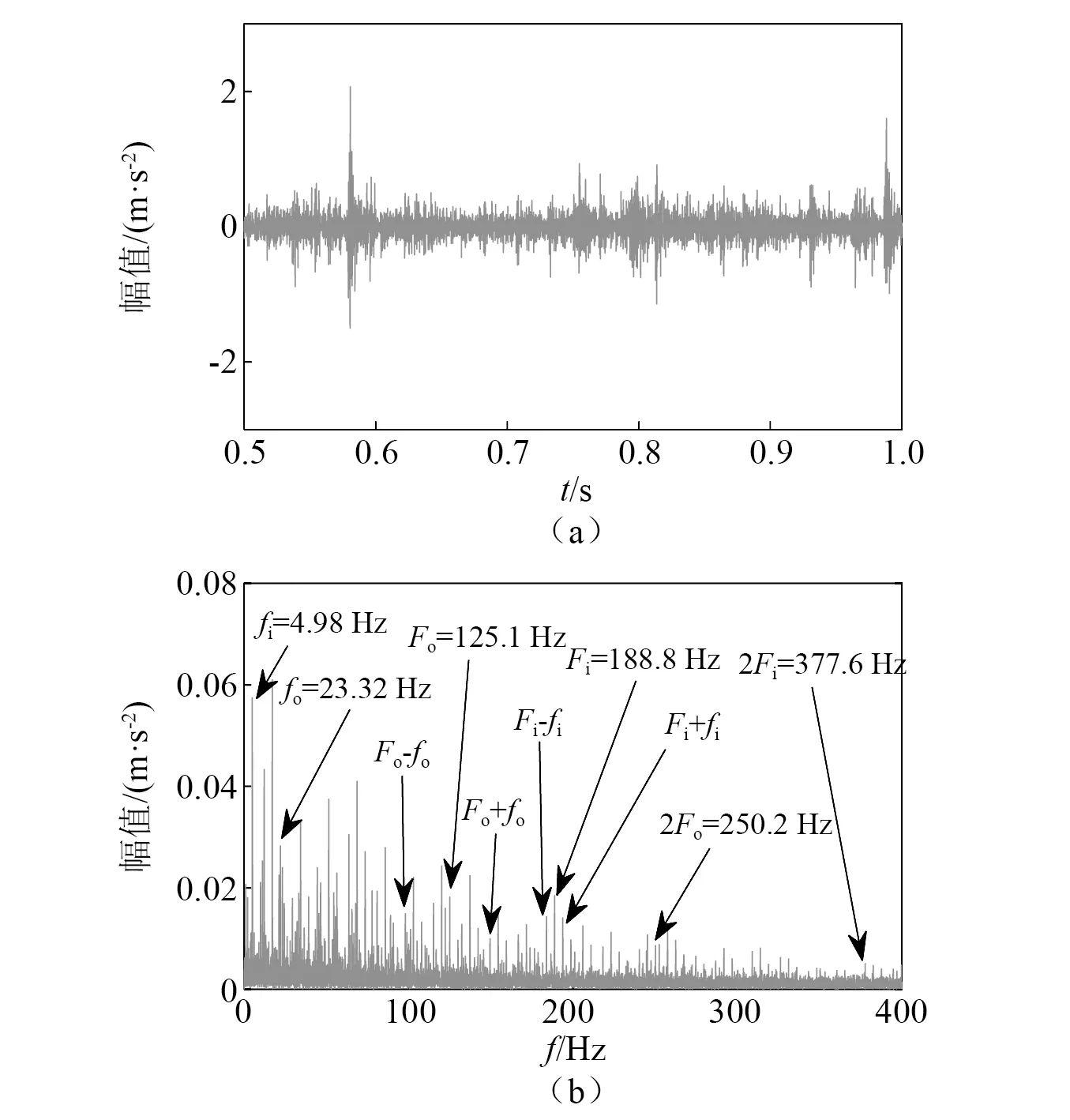
图17 反向旋转时内、外圈复合故障时域波形和包络谱试验结果Fig.17 Experimental results of time domain waveform and envelope spectrum of compound fault inner and outer rings in reverse rotation
4 结 论
(1) 基于本文建立的中介轴承内圈多点故障、外圈多点故障和内外圈复合故障模型数值模拟获得的故障特征频率值与试验值的误差均小于1%,获取的时域波形及包络谱中的时频信息分布规律与试验一致,验证了本文所建立模型的准确性。
(2) 同一个滚子在旋转的整个过程中会与不同的故障相撞形成脉冲,两次脉冲在时间上会有间隔,时域图中表现出脉冲叠加的现象。由模型计算得到的同一故障、不同滚子形成的脉冲的时间间隔数值与理论分析值基本一致,且由同一故障与不同滚子相接触形成的相邻脉冲,其时间间隔为故障特征频率的倒数。
(3) 中介轴承内圈、外圈存在复合故障时,在时域波形和包络谱中可以看到复合故障信号中包括内圈故障信号及外圈故障信号,且每种信号皆受与其对应的转频的调制。
