基于MUSIC及波束成形算法的非线性Lamb波微裂纹成像与评估

张 凡，徐 旭，李义丰

(南京工业大学 计算机科学与技术学院，南京 211899)

板状结构在生产建设中被广泛应用于机械、化工、建筑、航空航天等领域[1-3]。在长期承受载荷的应力作用下，易产生疲劳损伤，继而发展成为有损于结构强度的宏观损伤，引发结构破坏，生产事故。因此，结构体的早期微裂纹检测是安全生产的重要保障手段[4-5]。

Lamb波是一种在薄板中传播的导波，具有传播距离长和对内部缺陷敏感的特点，被广泛地应用于板结构的无损检测领域中。传统的Lamb波检测技术多基于线性理论，根据缺陷引起回波的声速、衰减、相位、反射系数等特性的变化来实现损伤的检测，但对于早期的亚波长微裂纹不敏感[6-10]。结构中的微裂纹具有接触非线性效应，会在透射和反射波中产生高次谐波，这为微裂纹 定位和评估提供了新的可能性。

传统的基于Lamb波的损伤定位成像算法多采用飞行时间(time of flight,TOF)或基于损伤指数的概率损伤成像算法。Sohn等[11]通过使用16个PZT贴片传感器阵列并基于时间反转方法实现了对复合板中的缺陷检测。Huang等使用概率损伤算法高效地实现了板中损伤定位成像。Caterina等[12]对“T”型碳纤维增强层合(carbonfiber reinforced polymer，CFRP)结构的常规损伤进行了定位成像研究。此类算法都是基于稀疏阵列构建的，具有构建简单和计算量小的优点。TOF类算法需要人为地区分激励信号、损伤的回波信号以及边界反射信号波包，并通过测量损伤回波信号的飞行时间，计算损伤和激励源的位置，实现损伤定位成像。但是，微裂纹的回波幅值较小，易淹没在系统噪声和其他回波信号之中，难以准确地分别损伤回波信号，故而该类方法无法实现微小损伤的精确定位成像[13-16]。而概率损伤成像方法仅能对布置传感器时规划的检测路径上的损伤实现精确成像，而对规划路径外的损伤则不具备高精度的成像定位能力[17]。

近年来，基于非线性Lamb波的检测研究越来越引起研究者的关注。Jiao等通过对微裂纹混频非线性技术的研究，使用非线性Lamb波信号对板中微裂纹情况进行了检测；祝伟光等[18]利用非线性参数，对微裂纹生长方向的识别进行了研究；Hong等和Wang等[19]则分别对非线性Lamb波使用概率损伤算法和椭圆定位算法进行了微裂纹定位研究，但其算法定位准确性较差，定位精度不高。Lamb波在传播经过微裂纹时，会与损伤相互作用产生新的散射波。因此，通过布置传感器阵列，依托波达方向估计(direction of arrival,DOA)算法来实现损伤的定位成像。波达方向估计是一类使用阵列信号确定外界发射信源和阵列之间相对的方向信息的阵列信号处理方法，被广泛的应用于现代雷达、通信、汽车、声纳中。此类算法中最广泛的应用是利用噪声子空间正交性的多重信号分类(multiple signal classification,MUSIC)算法[20-24]，具有高分辨力、强抗噪声的特点。使用MUSIC算法进行阵列信号处理可以有效的解决非线性Lamb波的低幅值和易淹没在系统的非线性噪声中的问题，实现对微裂纹的高精度定位成像。

另外，微裂纹的损伤评估是结构健康检测的重要内容。鉴于微裂纹非线性效应产生的二次谐波容易被各种噪声的干扰所淹没，本文在使用多重信号分类算法获得损伤的准确定位后，进一步采用波束成形算法，实现对信号的空间滤波，进而提高损伤方向的信号强度，并根据接收波的非线性参数，完成对板中微裂纹情况的定量评估[25-26]。

1 理论基础

1.1 非线性Lamb波基本理论

Lamb波是一类在无牵引、均匀和各向同性板中传播的平面应变弹性波。其传播受Navier方程约束。

(1)

式中：λ0和μ0为材料的拉梅常数；ρ为密度；bi为每单位质量的力；u为位移；i，j为坐标索引。

针对材料的非线性，其应力应变关系可以表示为

σ=Eε(1+βε+…)

(2)

式中：E为弹性模量；β为二阶弹性系数；σ和ε分别为应力、应变。忽略二次以上的高阶项，代入一维波动方程，可得

(3)

式中：u为位移；x为波传播的距离；t为时间；c为波速。展开得

(4)

对于较小的振动幅值时，设其解得形式为

u(x,t)=u(0)+βu(1)

(5)

式中，u(0)，u(1)分别为通解和二阶摄动解。一般情况下，摄动解与传播距离成正比，故有

u(1)=xf(τ)

(6)

式中：f(τ)为任意一二阶可微且连续的函数；τ=t-x/c。

本文使用激励信号为正弦信号，故可表示为

u(0)=A1cos(f1t-k1x)

(7)

将式(6)、式(7)代入式(5)求解得

(8)

因此，式(5)可写作

(9)

设二次谐波分量为A2，则有

(10)

不同于材料本身的非线性，微裂纹引起的声学非线性而产生高次谐波的物理机制是接触声学非线性。Lamb波在传播经过微裂纹时，会牵引其界面而产生半波整流效应。这种半波整流效应源于接触部位刚度的不对称特性。在压缩过程中，微裂纹受Lamb波的作用而闭合，拉伸过程中，则会使微裂纹开放，使得在压缩过程中的刚度高于拉伸过程的。这意味着Lamb波的压缩过程可以传播过界面，而拉伸过程会受到界面的阻挡，而无法通过界面。该效应导致了在透射波和散射波中高次谐波的产生，会在激励频率的整数倍频率处产生分量。通过比较Lamb波信号的基波和二次谐波振幅，可以定性和定量的实现对微裂纹的评估。

图1 微裂纹的接触声非线性Fig.1 Contact acoustic nonlinearity of micro cracks

图1(a)和图1(b)中：虚线表示微裂纹的初始位置；实线表示在Lamb波的压缩和拉伸作用下，微裂纹左侧界面的实际位置。图1(c)为Lamb波通过微裂纹后的半波整流效应示意图。尽管实际界面间的相互作用过程非常复杂，但其反射波非线性参数的形式皆可定义为二次谐波分量与基频分量平方的比值。故定义相对非线性参数β′，用以衡量微裂纹情况。

(11)

1.2 MUSIC算法基本理论

MUSIC算法从阵列接收信号的协方差矩阵分离出信号子空间和噪声子空间,而后利用信号方向向量与噪声子空间的正交性构建空间扫描谱,实现信号的波达方向估计。常用于信号接收的线状阵列建模如图2所示。

设线状阵列由N个间距为d的子阵元组成，远场有M个不相干的信源，其与阵列首阵元的法线方向所成夹角θ为入射角。阵列接收到的信号矩阵X(t)可以通过式(12)描述。

X(t)=A(θ)S(t)+N(t)

(12)

式中，A(θ)，S(t)及N(t)的表达式分别为

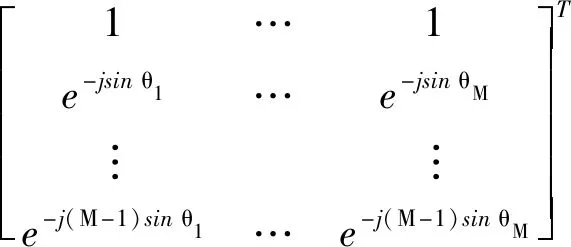
(13)

S(t)=[S1(t),S2(t),…,SM(t)]T

(14)

N(t)=[n1(t),n2(t),…,nN(t)]

(15)

式中：A(Θ)为线状阵列的方向矩阵；S(t)为M个从远场入射的信源所发射信号矩阵，并分别与阵列首个阵元的法线方向成夹角Θ=[θ1,θ2,…,θM]T；N(t)为噪声矩阵。

图2 线状阵列示意图Fig.2 Schematic diagram of linear array

接收信号的互相关矩阵为Rx=E[XXH]，其中H表示矩阵的共轭转置。假定噪声为互不相关的零均值加性的高斯白噪声。将式(12)代入后，可得

Rx=E[(A(θ)S(t)+N(t))(A(θ)S(t)+N(t))H]=
AE[SSH]AH+E[NNH]=ARSAH+RN

(16)

式中：RS=E[SSH]为信号相关矩阵；RN=σ2I为噪声相关矩阵；σ2为噪声信号的方差；I为M×M的单位矩阵。现假定协方差矩阵Rx的特征值为{λ1,λ2,…,λN}，所对应的特征向量依次为{q1,q2,…,qN}。在多信源不相干且信源个数Mλ2>…>λM>…λN，其中,M个较大的特征值对应于信号空间，余下的N-M个较小的特征值对应于噪声空间。信号特征值和噪声特征值对应的特征向量分别为信号特征向量和噪声特征向量。

根据特征值和特征向量定义

Rxqi=λiqi

(17)

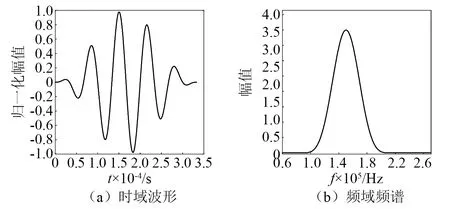
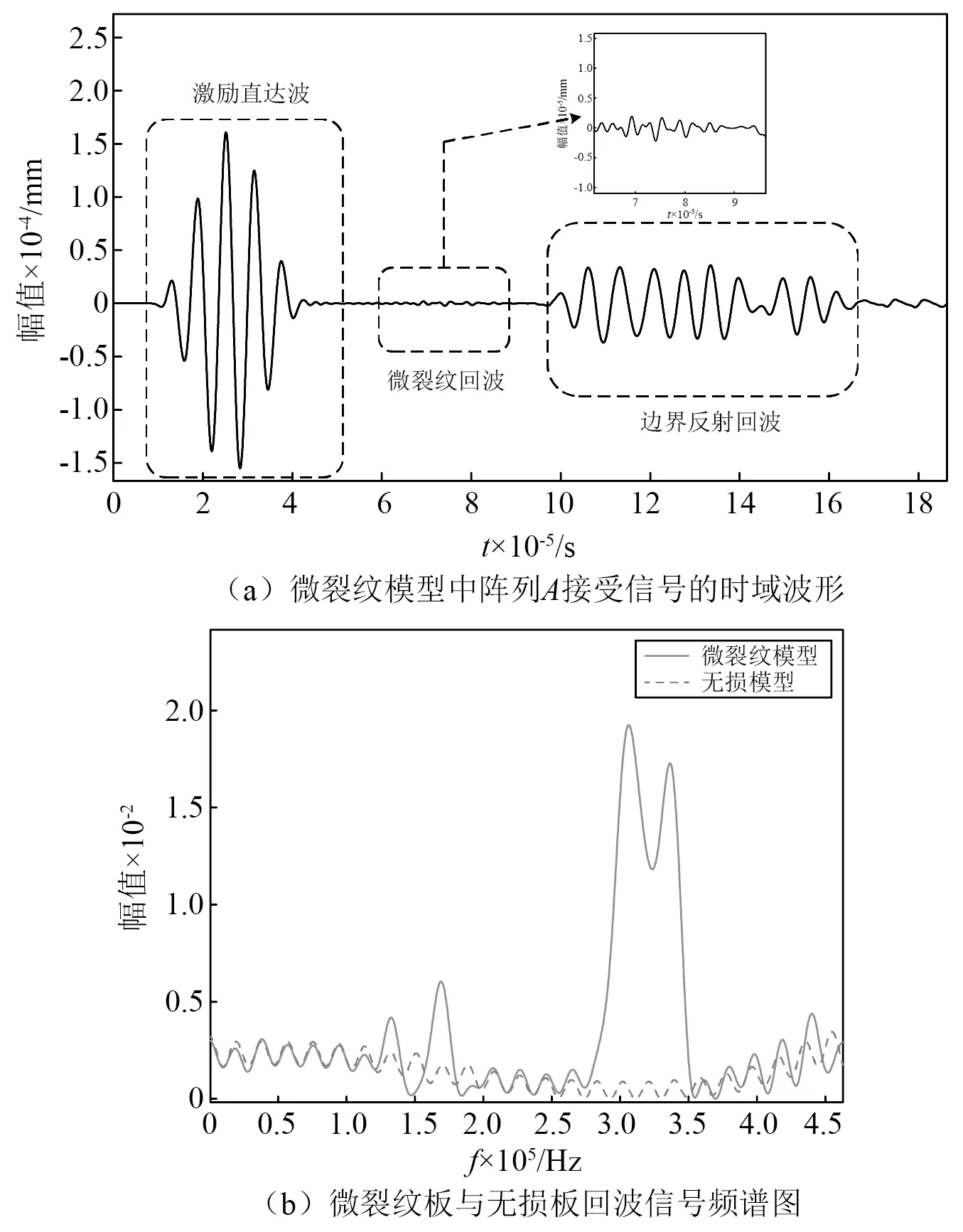
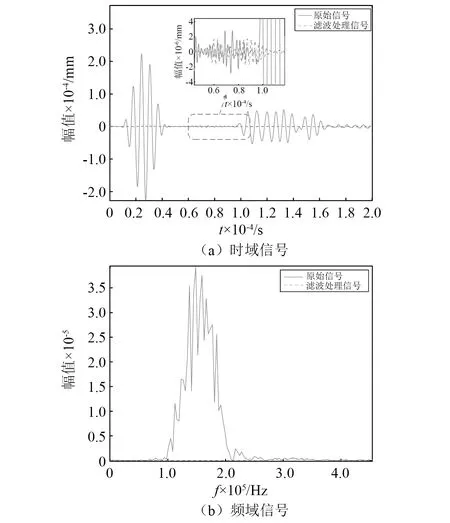
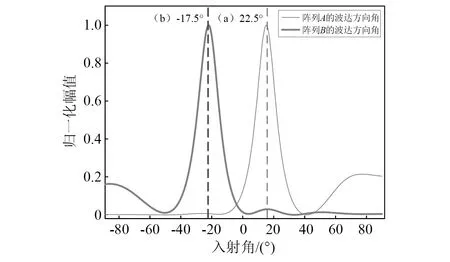
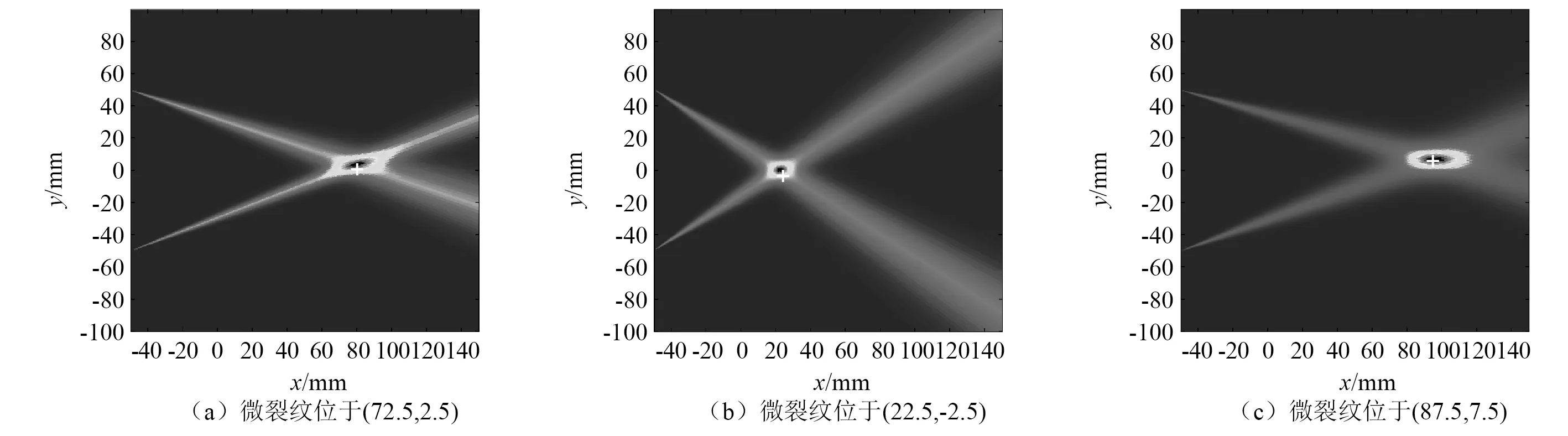
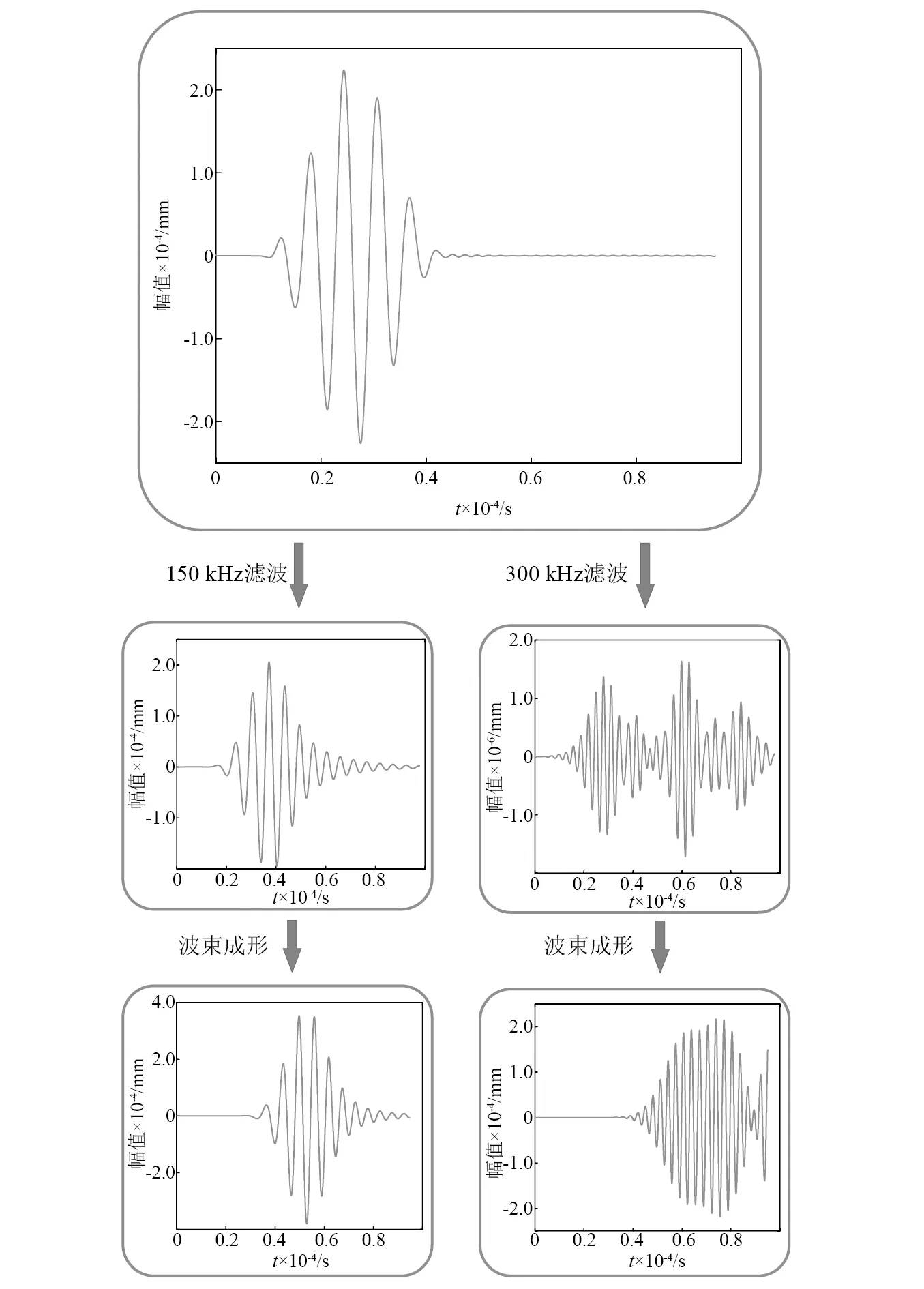
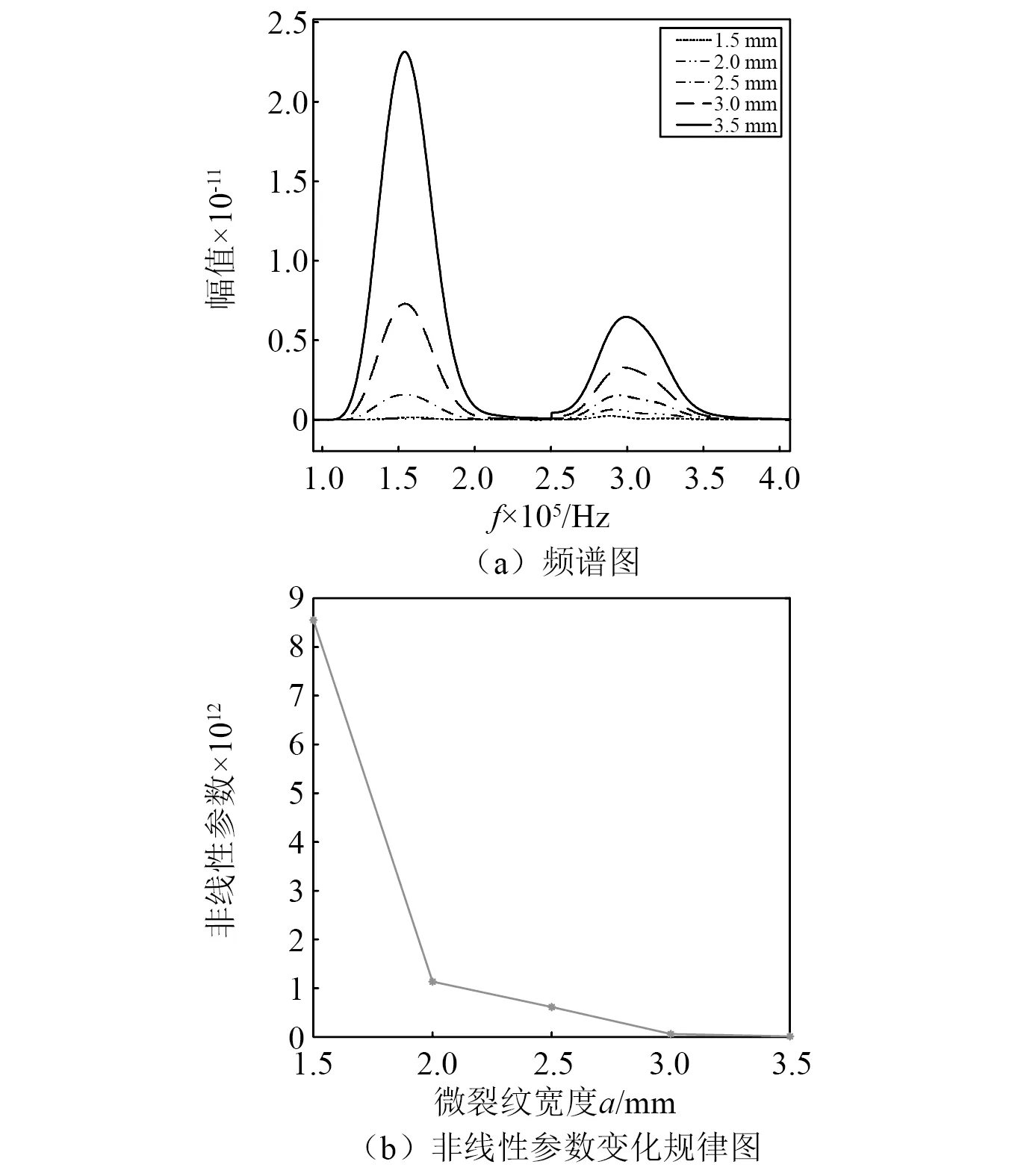
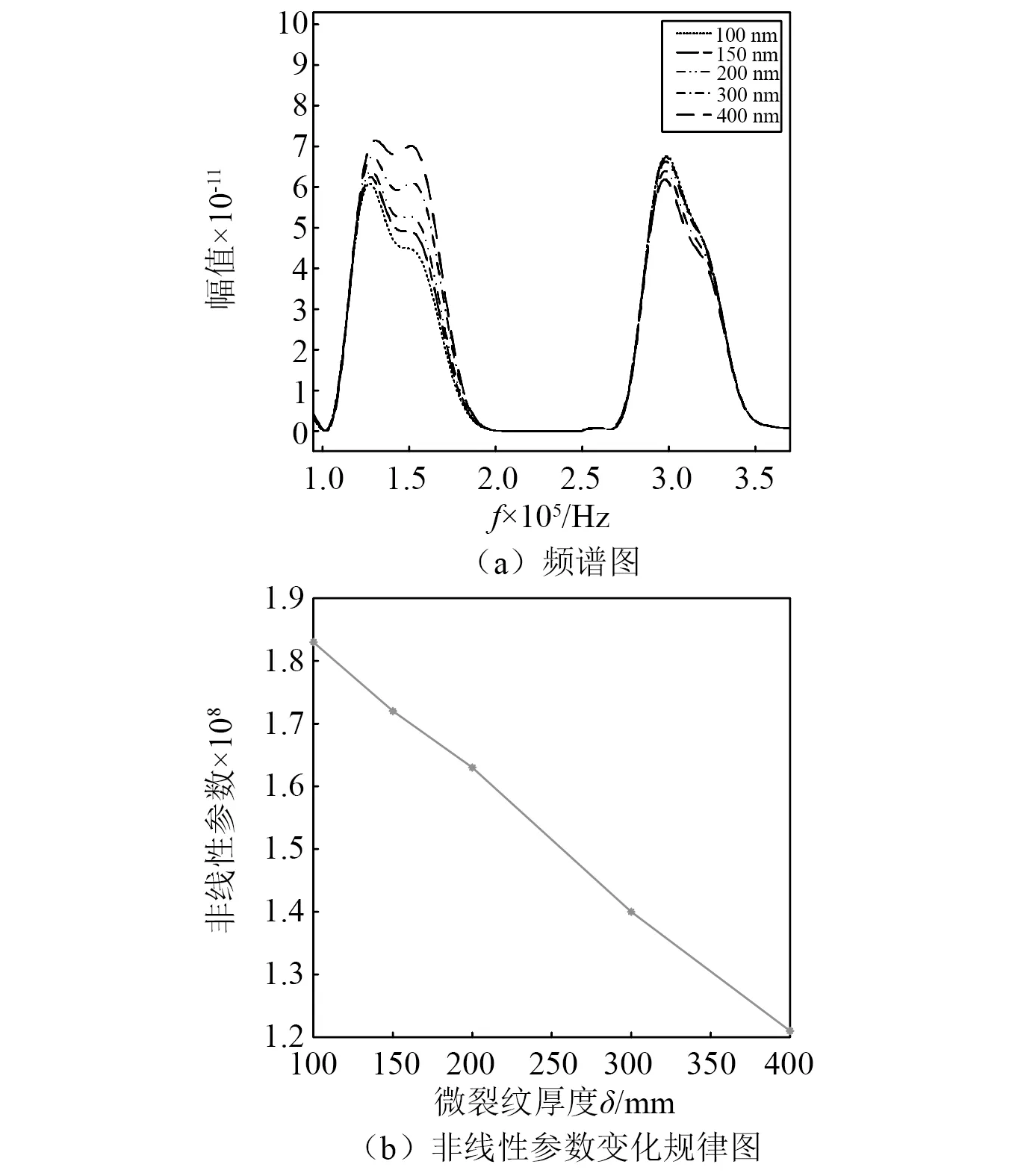
对于M

Rxqk=λkqk=σ2qk

(18)

此时，将式(16)左右同乘qk可得

Rxqk=(ARSAH+σ2I)qk=ARSAHqk+σ2qk

(19)

(20)

AHqk=0

(21)

式(21)表明，噪声特征向量和阵列方向选择向量相正交。利用此正交特性，通过求解阵列信号的互相关矩阵对应的噪声特征向量EN，对信源到达方位角进行搜索，生成空间谱，实现波达方向估计。空间谱函数定义为

(22)

本文使用以上的MUSIC算法对非线性Lamb波回波信号进行处理，以实现对微裂纹的高精度定位成像。

在实际检测中，声学非线性效应很微弱，产生的二次谐波的幅值会远远小于基波的幅值，极易被淹没在噪声中。因此，为实现对微裂纹的定性和定量分析，需要开发针对微弱的二次谐波的信号的增强算法和抗干扰检测技术。本文通过提取非线性Lamb波的高次谐波信号及对非线性参数的分析，完成对微裂纹的定位成像和损伤程度评估。

1.3 波束成形算法

线状阵列接收到信号后，通过将多个阵元接收到的数据进行延时、加权、求和等一系列处理，使得处理后的信号对指定的方向具有较高的增益而对其他方向的信号的增益较低，实现空间滤波。传统波束形成通常按以相移波束形成或时延波束形成的方法，选择合适的加权信号，使得指定方向的信号被加强而其他方向接收到的信号被减弱，这有利于从阵列信号中完成对幅值较低，易被淹没在噪声中的微裂纹信号的提取。

本文采用基于时延加权求和方法的波束成形算法(conventional beamforming,CBF)实现对微裂纹信号的空间滤波，通过式(23)实现对阵列信号的波束成形。

(23)

式中：n为阵列的序号；N为阵列的阵元数；θ0为所形成的波束的指向角；f和c分别为Lamb波的频率和波速。

通过该波束成形算法的使用，可降低阵列信号中其他方向杂波所造成的干扰，确保非线性参数评估方法的准确性。

2 有限元仿真模型

本文使用有限元软件ABAQUS 建立了三维铝板的仿真模型，通过显式动力学分析法对非线性Lamb波在铝板中的传播进行分析。铝板的物理参数如表1所示，其几何参数为600 mm ×600 mm ×4 mm，如图3所示。通过嵌入Cohesive界面单元创建埋藏微裂纹模型，其上下界面设置为硬接触，且为法向无位移的面-面相互作用。以板的几何中心点作为原点，长宽方向分别为坐标系的x轴和y轴方向，厚度方向为z轴方向。以坐标(-50,50) 的A1点，和坐标(-50,-50)的B1点为首阵元，5 mm为阵元间距，分别设立由7个阵元构成的A、B两个传感器阵列。于坐标(-50,0)处施加对称载荷，在板中激发出单一S0模态的Lamb波。激励载荷信号为中心频率150 kHz的经5周期汉宁窗调制的正弦波信号，时域波形和频域频谱如图4所示。在本文中基频信号的群速度约为5 440 m/s，波长为36.3 mm,与微裂纹相互作用产生的300 kHz非线性Lamb波二次谐波信号的波速约为5 210 m/s，波长为17.4 mm。

表1 铝板材料参数Tab.1 Material parameters of aluminum plate

图3 三维铝板及埋藏裂纹示意图Fig.3 The schematic of 3D aluminum plate model and buried crack damage modes

图4 激励信号Fig.4 Excitation signal

3 仿真结果与分析

3.1 微裂纹定位成像

于板中(87.5,7.5)处设立埋藏微裂纹(见图3)。零厚度Cohesive界面单元的长度l为5 mm，高度h为3 mm。首先，对无损模型和含微裂纹模型的有限元仿真结果进行对比分析，验证Lamb波的非线性效应。图5(a)为微裂纹模型中阵列A首阵元所接收信号的时域信号，图5(b)为首阵元所接收回波信号的频谱。可见，微裂纹板相较于无损板，二倍频处产生了由微裂纹而引起的非线性信号。

图5 传感器阵列接收的信号Fig.5 Signal received by sensor array

接收到的回波信号为同时包含基波和二次谐波分量混叠波形，为了实现损伤定位，需要滤除不能表征微裂纹的基波信号。本文设计并使用巴特沃尔兹带通滤波器提取二次谐波信号，回波信号的波包通过滤波器前后对比时域波形图及频谱图，如图6所示。图6表明了带通滤波器在有效滤除了基波信号的同时，较好地保留了二次谐波分量。

滤波后的微裂纹回波信号经过MUSIC算法处理后，可获得微裂纹位置与阵列的法线方向夹角。为实现损伤定位成像，需通过两个不同位置的传感器阵列，分别获得微裂纹相对于两个阵列的不同方向角，而后利用交叉定位的方法来实现对微裂纹的定位。由以A1点和B1点为首阵元的两个线状阵列A、B，分别计算得到这两个阵列所接收信号的空间谱，结果如图7所示，两虚线分别表示微裂纹相对于阵列A、B的实际入射方向角。

图6 滤波前后首阵元接收到的信号Fig.6 Original and filtered signals received by the first element of array

图7 不同阵列回波信号处理后的空间谱Fig.7 Spatial spectrums calculated from different arrays’ echo signal

利用不同位置阵列所提取到的空间谱，分别对位于(72.5,2.5) 、(22.5,-2.5) 和(87.5,7.5)处的微裂纹进行MUSIC算法定位成像，结果分别如图8(a)～图8(c)所示，其中‘+’号标注为实际损伤的位置。图8表明通过使用MUSIC算法处理非线性Lamb波信号可以获得优秀的微裂纹定位成像。

在实际检测中，微裂纹的回波信号幅值较低，易被淹没在系统噪声和其他回波干扰信号中，故难以使用传统检测方法实现定位。对无噪声的仿真信号中添加高斯白噪声以模拟真实环境中接收到的信号。信噪比为25 dB时的信号如图9所示，可见回波信号被淹没在噪声中。在此情况中，传统检测方法不具备准确区分回波信号和杂波信号的能力。

图8 基于MUSIC算法的非线性Lamb波微裂纹成像图Fig.8 Micro crack imaging by using nonlinear Lamb wave based on MUSIC algorithm

图9 25 dB信噪比时的回波信号Fig.9 Echo signal at SNR of 25 dB

本文的MUSIC算法具备较强的抗噪声能力，在上述信噪比为25 dB的情况下，使用MUSIC算法对位于(87.5,7.5)处的微裂纹进行定位成像，结果如图10所示。该图表明在低信噪比情况下，基于MUSIC算法的非线性Lamb波对微裂纹仍具备较好的微裂纹定位成像能力。

图10 信噪比为25 dB时微裂纹定位成像图Fig.10 Imaging of micro crack location at SNR of 25 dB

3.2 微裂纹尺寸评估

利用非线性MUSIC算法，可以从回波信号中获得微裂纹的位置信息。为了减少噪声和其他方向反射Lamb波的干扰，本文使用波束成形算法对信号进行空间滤波，以提取获得指定方向角上的回波信号。通过分析特定角度的回波信号，在微裂纹成像的基础上，进一步实现对微裂纹情况的评估。

对坐标位于(72.5,2.5)处的微裂纹进行分析。首先，对上文中的微裂模型进行有限元分析，并通过波束成形算法对阵列信号进行空间滤波。图11为对阵列所接收原始信号中的基频信号及二倍频信号分别进行滤波及波束成形处理后所得到的波形图。

图11 波束成形处理后的波形图Fig.11 Waveform obtained after beamforming processing

本文分两种情况，即分别单独改变Cohesive界面单元的高度(h)、厚度(δ)两组模型进行仿真分析。第一组仿真分析为保持Cohesive界面单元的长度l与厚度δ不变(h=5.0 mm,δ=300 nm)，选择不同高度(h=1.5 mm,h=2.0 mm,h=2.5 mm,h=3.0 mm,h=3.5 mm)的裂纹模型；第二组仿真保持微裂纹长度l与高度h不变(l=5.0 mm,h=3.0 mm)，选择不同厚度(δ=100 nm,δ=150 nm,δ=200 nm,δ=300 nm,δ=400 nm)的裂纹模型进行分析。

图12为进行第一组仿真分析得到的结果，图12(a)对不同高度的微裂纹模型所接收的信号波束成形处理后得到的频谱图，图12(b)为对不同高度的微裂纹采用式(11)计算所得的非线性参数。图12(b)表明随着微裂纹的高度增加，回波信号的非线性参数会随之而单调递减。根据接触非线性理论，当微裂纹的高度增加时，只有在微裂纹的端点附近处的界面会受到Lamb波的作用，产生持续的拍击。微裂纹高度上的变化并不会引起拍击面积的大幅度变化，在频域上表现是二次谐波的幅值随微裂纹高度不同的变化较小。而基波主要是由裂纹的反射产生的，其幅值随着裂纹高度的增加而增加，且变化明显。因此，表现为随着微裂纹高度的增加，回波信号的非线性参数单调递减。

图12 对不同高度的微裂纹回波信号波束成形处理Fig.12 Beamforming processing of echo signal with different height h of microcrack

图13为进行第二组仿真分析得到的结果，图13(a)为对不同厚度的微裂纹模型所接收信号波束成形处理后得到的频谱图，图13(b)为对不同厚度的微裂纹采用式(11)计算而得的非线性参数。该图表明，随着微裂纹的厚度增加，回波信号的非线性参数会随之而单调递减。根据接触非线性理论，当微裂纹的厚度增加时，基波幅值在增加，而能产生接触非线性的区域将减少，导致了二次谐波幅值的降低，因此，随着微裂纹厚度的增加，回波信号的非线性参数单调递减。

图13 对不同厚度微裂纹回波波束成形处理Fig.13 Beamforming processing of echo signal with different deepths d of microcrack

4 结 论

本文研究了非线性Lamb波检测中微裂纹定位成像和评估问题。利用有限元模拟分析方法，建立了包含埋藏微裂纹的薄铝板结构模型。利用多输入信号算法，实现了对埋藏微裂纹的定位成像，并通过向接收信号中人工添加高斯白噪声来模拟实际检测信号，验证了该MUSIC算法具有非常好的抗干扰损伤定位成像能力。继而结合波束成形算法，对阵列信号进行空间滤波处理，可有效提高微裂纹所在方向回波信号的幅值；通过频谱分析可知该回波信号的非线性参数与微裂纹高度呈递减关系，与微裂纹厚度呈下降关系。说明回波信号的非线性参数可以有效反映板中损伤的情况，通过分析该非线性参数可实现对微裂纹损伤情况的评估。