下击暴流作用下输电线路导线风偏响应特性研究
2022-12-01刘春城
刘春城,侯 萌
(东北电力大学 建筑工程学院,吉林 吉林 132012)
对近年来的输电线路的风偏闪络跳闸事故分析发现,发生事故的区域均出现了局部的中小尺度强对流天气,即下击暴流[1]。下击暴流为雷暴天气中强烈的下沉气流冲击地面,并由冲击点沿地表向四周扩散的极具突发性和破坏性的一种强风,瞬时风速超过30 m/s[2],会在输电线路的局部区域内产生很大的风荷载,使绝缘子串和导线的风偏位移峰值突然增大,造成风偏闪络事故,经济损失重大。并且下击暴流的发生频度较高,其中水平尺度较小的微下击暴流在雷雨天气发生的概率可达60%~70%[3],已被证实对大量工程结构物产生较大的影响,尤其是对输电线路的影响巨大。目前关于下击暴流作用下输电线路风偏响应的研究还很不成熟,在已有的输电线路设计规范里也没有相关规定。因此为保证高压输电线路的安全稳定运行,开展下击暴流风场特性及其对输电线路风偏响应的影响研究,对指导输电线路的防风偏设计和控制具有重要的科学意义和工程应用价值。
目前关于输电线路风偏响应的研究大多数都基于常规边界层风场[4-8],这部分的研究已经相对成熟。而关于下击暴流作用下的输电线路风偏响应研究还不完善,楼文娟等[9]结合矢量合成法和谐波叠加法对运动雷暴冲击风风场中输电线路风荷载计算参数开展了全面的研究,得到了输电导线风荷载的完整表达式。吕中宾等[10]对雷暴冲击风风场进行数值模拟,对雷暴冲击风作用下的导线风偏进行求解,并就风暴中心与线路的相对位置和风暴结构参数对计算结果的影响进行讨论。冯珂等[11]通过采用Oseguera模型,建立下击暴流的风速模型,采用Newmark-β法研究了输电导线下击暴流风致响应的特点和规律。王嘉伟[12]考虑输电线路相邻跨间的联动作用,建立了输电线路与绝缘子的耦合有限元模型,探讨冲击风场下输电线路的风偏响应特征及挂点处的不平衡张力,并开展了雷暴冲击风参数影响分析。
以上研究主要是改变了风暴参数(射流直径、射流速度等)以及射流中心到线路的垂直距离,并未考虑射流倾角变化对风场特性和线路风偏的影响,也未考虑线路结构参数(如档距、导线张力等)变化对风偏的影响。本文基于已有研究基础上开展了下击暴流作用下输电线路风偏响应特性研究,考虑了下击暴流射流倾角变化对其风场特性的影响。同时以四档输电线路为例,分析了射流倾角、线路档距和导线张力变化对绝缘子串风偏角及档距中央导线风偏位移的影响,研究成果为雷暴多发地区输电线路的防风偏设计提供参考。
1 下击暴流风场的数学模型
下击暴流由于发生的瞬时性和随机性,现场实测很难开展,实测结果缺乏普遍适用性。在缺乏实测数据的条件下,解析理论模型作为重要的分析手段,得到了广泛应用,已满足实际工程应用的需求。
1991年,Vicroy[13]依据Oseguera等[14]模型通过分析改进从而提出了更加贴合实际的下击暴流平均风速模型。Vicroy模型为
(1)
式中:Vmax为下击暴流最大径向风速;zmax为风速最大时的竖向高度。
1998年Wood等[15]通过物理模拟下击暴流,提出了不完全的半经验下击暴流风场模型,Wood模型为
(2)
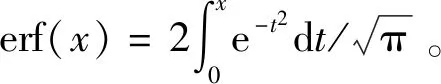
2 下击暴流风场的CFD数值模拟
2.1 几何模型参数设置
本文采用的模型为三维冲击射流模型。Kim等[16]将不同参数设置的冲击射流模型模拟结果与现场实测等数据进行对比,发现射流初速度Vjet=29 m/s,射流直径Djet=600 m,下击暴流入口高度取H=4Djet,这样的初始条件模拟结果同足尺的实测数据有极佳的吻合,考虑到射流的充分发展又兼顾计算资源的消耗,因此本文参考文献[17]在下击暴流模拟中选用的几何缩尺1∶2 000,速度缩尺1∶3和时间缩尺1∶1 000[18],这样缩尺条件下的数值仿真结果与经验剖面和早期的CFD模拟结果吻合较好。
考虑下击暴流在空间上的对称性,通过设置对称边界来计算整个风场模型的1/4即可,射流倾角为0°下击暴流风场计算域的剖面图,如图1所示,计算域设置为长10Djet、宽10Djet、高6Djet。
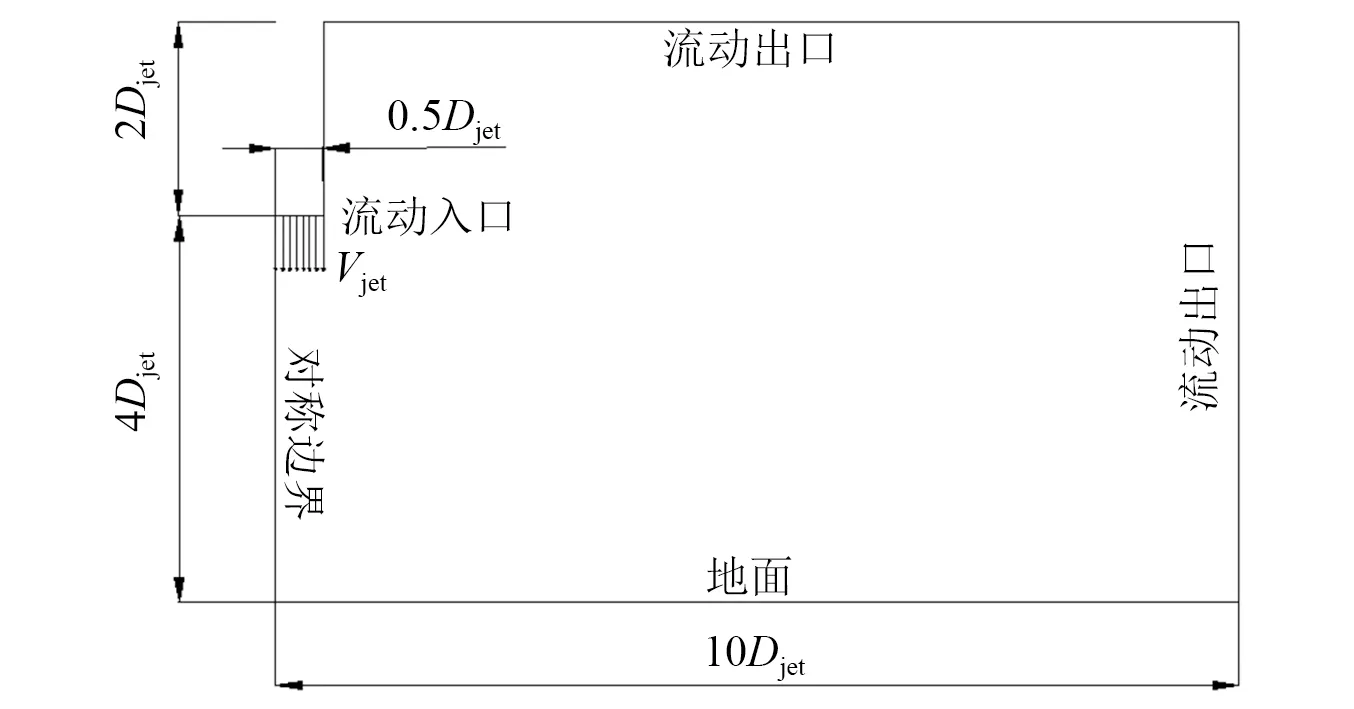
图1 计算域剖面图Fig.1 Cross section of computational domain
2.2 计算域边界条件设置
Fluent模拟中,边界条件的设定尤为重要,会对数值计算产生重要影响。计算域的边界条件设置如表1所示。

表1 边界条件设定Tab.1 Boundary condition setting
2.3 网格划分及湍流模型选择
在ICEM CFD模块中划分结构化网格,在近壁面边界层处加密网格,从而使冲击射流在边界层区域内得到充分的发展。第一层网格距壁面的距离为2×10-5m,每层网格间的竖向增长率为1.2,在靠近壁面区设置10层~15层的近壁面网格,从而让y+≤1,y+定义见式(3),能够在黏性子层中进行求解。湍流模型选用结合k-ω模型在近壁面区计算优点和k-ε模型在远场计算优点的SSTk-ω模型。
(3)
式中:Δy为首层网格至壁面的距离,m;v为空气黏性系数,m/s2;τw为壁面切应力,Pa。
2.4 下击暴流风场分析
2.4.1 数值模拟验证
将本文基于SSTk-ω模型模拟所得到的r=1.0Djet和r=1.25Djet处的竖向风剖面与Vicroy模型和Wood模型两种经验模型求得的竖向风剖面进行对比,其中对径向风速V与入口速度Vjet进行了归一化处理,高度z和射流管直径Djet进行归一化处理,如图2所示。
由图2可知,本文模拟的竖向风剖面与Wood模型和Vicroy模型在近地面处吻合较好,沿高度分布趋势也保持一致。本文模拟风剖面与其他两种经验风剖面在r=1Djet极值风速的对比,如表2所示。
在r=1.0Djet处极值风速相对误差在1.5%以下,说明了本文模拟的精度与正确性,为下文的模拟研究奠定了基础。
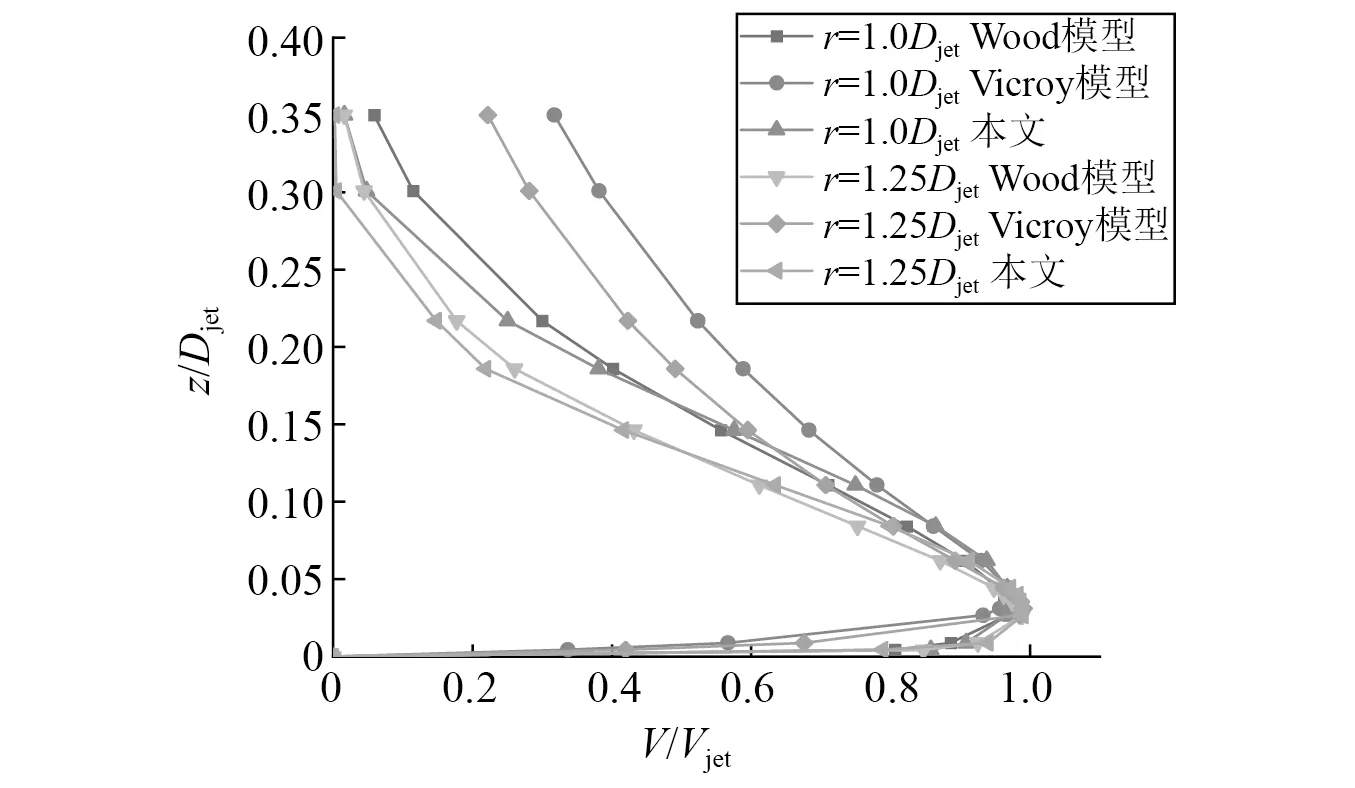
图2 竖向风剖面与经验模型对比Fig.2 Comparison of vertical wind profile and empirical model
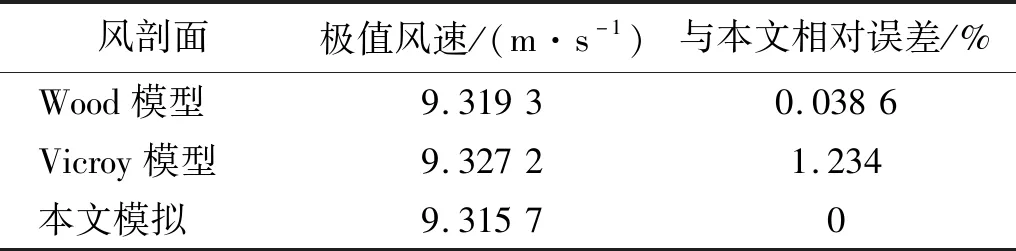
表2 极值风速误差表Tab.2 Error table of extreme wind speed
2.4.2 风场瞬态特征
选取射流倾角为0°,即射流口垂直于地面的风场情况。计算结果如图3所示。下击暴流发展过程与实测下击暴流的生命周期基本一致,表现出生成阶段、下沉阶段、冲击阶段、扩散阶段的特征明显,选取这4个阶段对应的时间点作为分析对象详细分析下击暴流的特点。

图3 不同时刻风速云图Fig.3 Cloud chart of wind speed at each time
(1) 在时间为100 s~230 s时,为下击暴流生成阶段和下沉阶段,在230 s时下沉气流前端刚接触到地面,下击暴流初始射流速度为29 m/s,气流从射流口向正下方冲击,下沉气流由于周围气体的阻碍作用,在下沉气流前端形成涡旋。最大速度出现在下沉气流前端涡旋中心位置,可达34.2 m/s。
(2) 在时间为230 s~400 s时,为下击暴流冲击地面加速阶段,下沉气流撞击地面,以涡旋的方式向四周发散,并且在涡旋的上方存在面向射流中心的径向速度。当下沉气流刚刚撞击地面时,会在距离地面较高处产生一个较大的涡旋,随着气流向四周发散,这个涡旋的高度会逐渐降低,与近地面冲击气流相互影响,速度相互叠加,致使气流速度逐渐增大,导致了距射流中心径向距离在1.0Djet~2.0Djet的近地面处产生了极强的向四周发散的径向风速,在330 s时风速在涡旋加速效果作用下达到最大,达到37.8 m/s,随着涡旋的离开,近地面的风速开始降低。
(3) 在时间为400 s~900 s时,为下击暴流的扩散阶段,射流前端涡旋继续向四周行进,在这个行进的过程中,涡旋高度有所升高、影响范围变大,但强度逐渐减弱,在900 s时涡旋底部近地面处的最大风速衰减到14.1 m/s;在1 200 s时,冲击射流风场前端涡旋开始消散;在1 500 s时,冲击射流风场前端涡旋已经基本上完全消散。
2.4.3 径向风速的竖向风剖面
在下击暴流风场发展完全后,经过归一化处理不同径向位置r处径向风速V随高度z变化的规律,如图4所示。
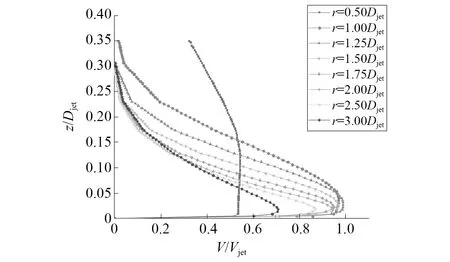
图4 径向风速的竖向风剖面Fig.4 Vertical wind profile of radial wind speed
由图4可知,最大径向风速Vmax发生在r=1.25Djet处,高度z在0.02Djet~0.03Djet,由几何缩尺为1∶2 000可换算为12 m~18 m,约为0.99Vjet。
图4中,r=0.5Djet位置处与其他位置处的竖向风剖面明显不同。这主要是因该位置正好处于射流口侧壁面边界的正下方,由于地表存在阻碍作用,下沉气流在此处处于刚刚撞击地面还未完全向四周发散的时候,因此在近地面的风速与其他近地面风速发展完全的径向位置相比较小,而在r=0.5Djet位置高度较高处由于射流口的能量输入风速主要是竖直向下的,向下的气流与周围空气作用,在水平方向上产生一定的水平发散气流,导致了在r=0.5Djet位置处径向风速沿高度变化的规律与其他径向位置有比较明显的差异。
在r=1.0Djet~3.0Djet时,径向风速V随高度z的增加而增加,在达到最大值后,V并不会立刻减小,而是在一定高度范围内保持极值风速,且距离射流中心越近,保持极值风速的高度越大。产生该现象的主要原因是由于下沉气流冲击地面后向四周扩散,由于地表存在物体阻力而引起流体在靠近地表一侧的速度减小,而在边界层区域内必须考虑黏性力,导致在较高处的流体流速也会受到黏性力的阻碍作用,两层流体之间形成的速度差较小,从而产生以上规律。
2.4.4 径向风速的径向风剖面
在下击暴流风场发展完全后,经过归一化处理不同高度z处径向风速V随径向距离r变化的规律,如图5所示。
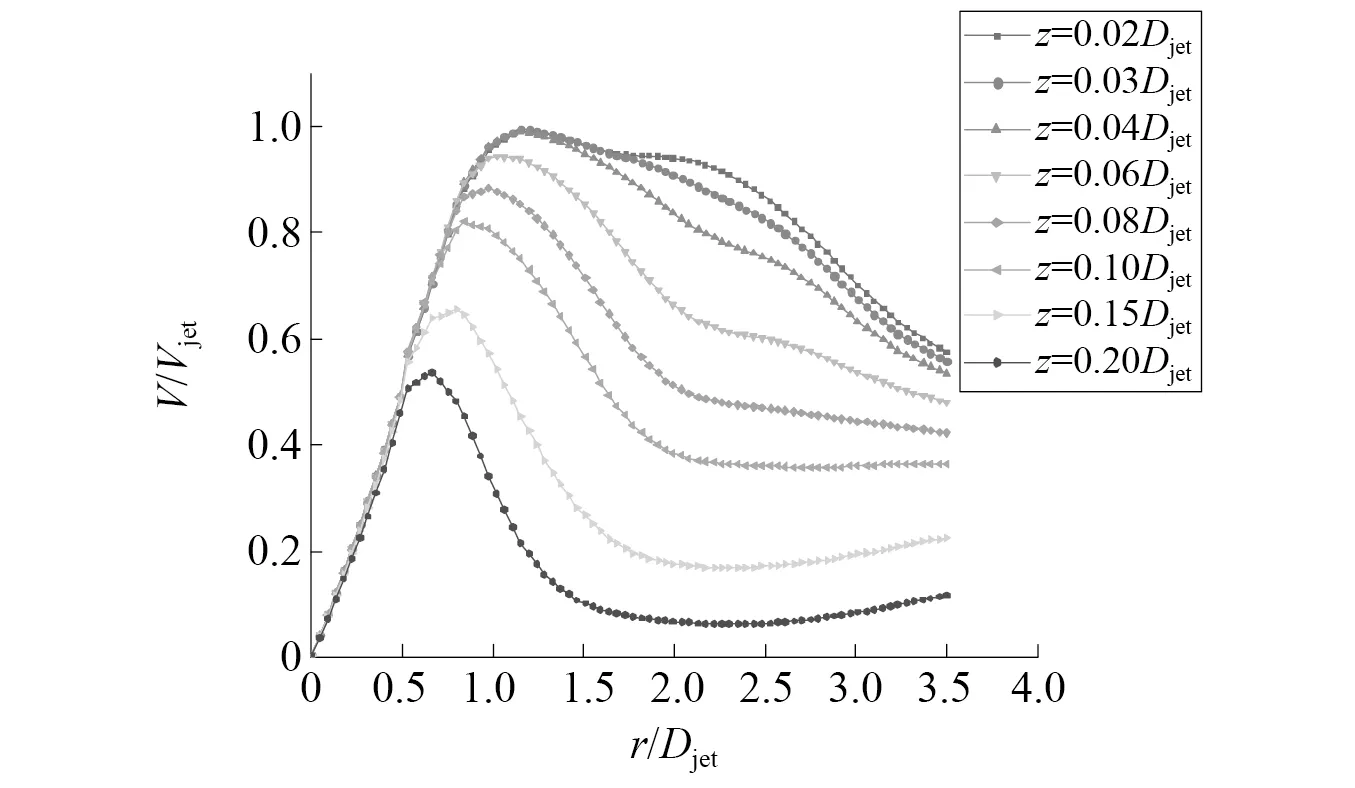
图5 径向风速的径向风剖面Fig.5 Radial wind profile of radial wind speed
由图5可知,径向风速最大值出现在高度z=0.02Djet~0.04Djet,r=1.0Djet~1.25Djet,约为0.99Vjet。虽然三条曲线的峰值基本相同,但z=0.04Djet的曲线明显比z=0.02Djet和z=0.03Djet两曲线随径向距离衰减的快。随着高度的增加,在达到峰值后随径向距离衰减的更快,并且高度越高的曲线达到峰值的速度越快。
通过对下击暴流风场特性的研究,得到了径向风速的竖向和径向风剖面变化规律,为输电线路风偏响应特性分析奠定了基础。
2.5 射流倾角对风场影响分析
2.5.1 竖向风剖面对比分析
在下击暴流风场发展完全后,经过归一化处理后射流倾角为10°和20°两种风场径向速度的竖向风剖面以及风暴前缘的径向位置分别为r=1.0Djet,r=1.25Djet和r=1.5Djet处不同倾角下竖向风剖面的对比图,如图6所示。
由图6可知,在射流倾角α为10°和20°风场中,径向风速最大值同样是发生在r=1.25Djet处,α为0°,10°和20°风场中的极值风速分别为28.5 m/s,27.99 m/s和27.9 m/s,因此对比三种风场在r=1.25Djet处的极值风速可发现,风场中的极值风速随着倾角的增加反而略微减小。并且随倾角α的增大,径向风速随高度增加而减小速率变缓,但极值风速所维持的高度区间变小,因此会发生在近地面处倾角α为0°风场的风速较大,但随着高度的增加,倾角α为10°和20°风场的风速较大,在55.8 m处倾角α为10°风场的风速开始大于倾角α为0°风场的风速,在39.9 m处倾角α为20°风场的风速开始大于倾角α为0°风场的风速,所以在分析风速沿竖向高度变化时要考虑射流角度的影响。
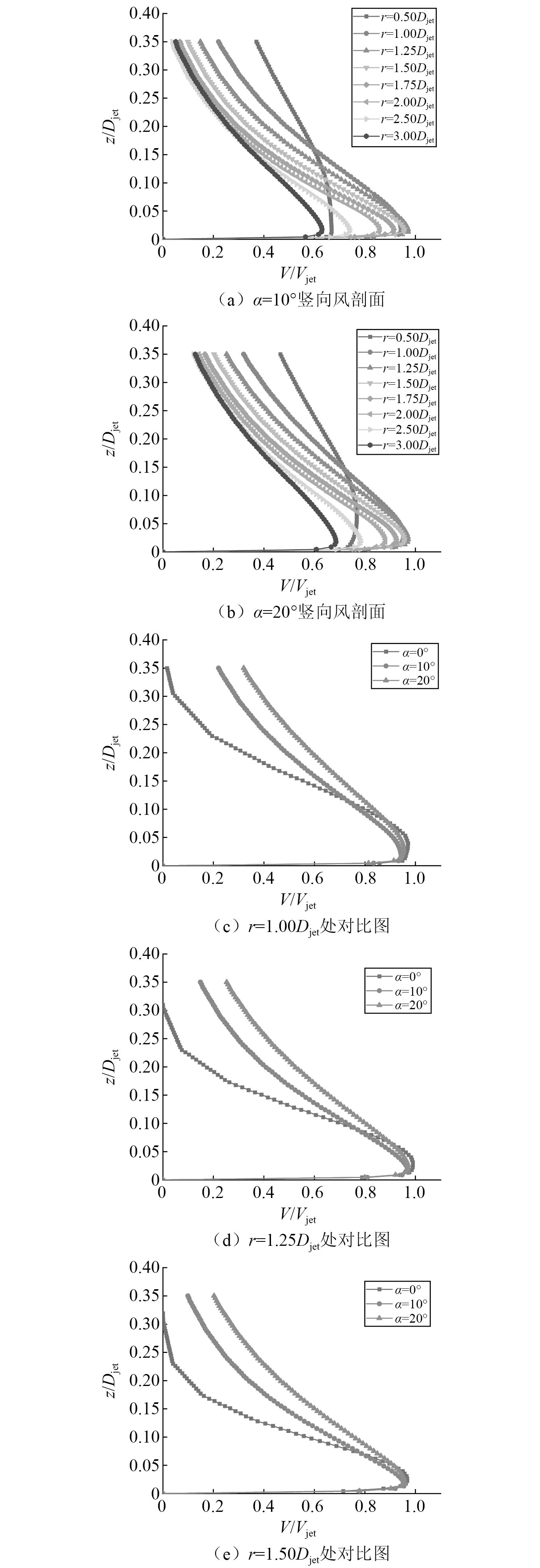
图6 带倾角风场竖向风剖面Fig.6 Wind profile of wind field with dip angle
三种风场竖向风剖面随射流倾角的变化规律主要是由于当射流倾斜时,更多的气流从前侧逸出,使得射流倾角大的射流风速沿高度下降得比射流倾角小的慢,在地面处风场所影响的范围高度较高。并且随着倾角的增加,射流口到地面的距离变大,气流在下沉的时候能量损耗增大,因此随着倾角的增大,风场的极值风速反而会略微的减小。
2.5.2 径向风剖面对比分析
在下击暴流风场发展完全后,经过归一化处理后倾角α=10°,α=20°两种风场径向速度的径向风剖面以及高度分别为z=0.02Djet,z=0.04Djet和z=0.06Djet处不同倾角下径向风剖面的对比图,如图7所示。
由图7可知,在z=0.02Djet处,射流倾角为10°和20°风场的极值风速基本相同,均小于射流倾角为0°的风场。但随着高度的增加射流倾角为20°风场的极值风速开始大于射流倾角为10°的风场,这与竖向风剖面分析所得的规律是相符合的。以z=0.06Djet处为例,可得射流倾角为10°和20°风场的径向风速在随径向距离的增加先增加最大值后呈近乎线性的衰减,并且衰减的速率明显较射流倾角为0°的风场小,这种规律在较高处更明显。在r=1.59Djet处射流倾角为10°的风场风速开始大于射流倾角为0°的风场;在r=1.33Djet处射流倾角为20°的风场风速开始大于射流倾角为0°的风场。
3 下击暴流作用下输电线路风偏响应
3.1 输电线路参数
依据王嘉伟的研究结果,为了使本文研究结果更具有一般性,选取耐-直-直-直-耐四档输电线路为实例。电压等级为1 000 kV特高压,直线塔呼高为50 m,耐张塔呼高为41 m,导线采用八分裂型式,导线型号为JL/G1A-500/35,复合绝缘子的型号为 FXBW-1 000/300,导线单元长度取10 m,经过试算,确定导线单元长度取10 m可满足收敛性和精度要求。
3.2 导线风荷载计算
大风作用下,多分裂导线各子导线以顺风向运动为主,且由于间隔棒的作用,各子导线运动基本同步。文献[19]表明,将分裂导线等效为单导线对于风偏响应计算而言具有足够的精度。因此本文模拟导线风偏时,将八分裂导线等效为一根导线,并将截面积、风荷载等参数做等效化处理,将导线离散成多段索单元,从风场中提取出每个单元处的风速,计算每个单元所承受的风荷载,然后施加到节点上。每个单元所受风荷载计算公式为
(4)
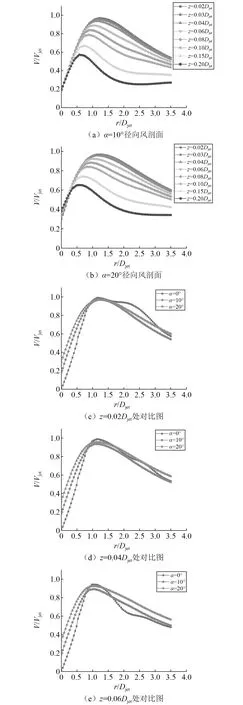
图7 带倾角风场径向风剖面Fig.7 Radial wind profile of wind field with dip angle
式中:Fx为单元所受风荷载;Vh为单元所在高度h处的风速;μsc为导线的体型系数,取1.1;βc为风荷载调整系数,取1.76;d为导线直径,l为单元长度。
3.3 风暴中心位置变化对线路风偏影响分析
3.3.1 计算工况
绝缘子串编号示意如图8所示。图8中:1号和5号为耐张绝缘子串;2号、3号、4号为悬垂绝缘子串。本文以悬垂串为研究对象。
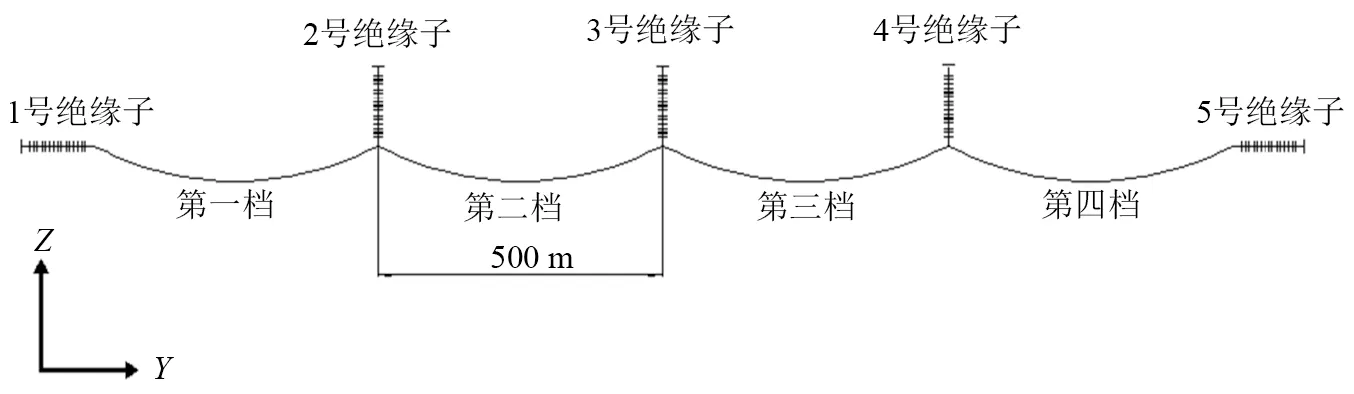
图8 绝缘子编号示意图Fig.8 Schematic diagram of insulator number
线路档距选为500 m,导线运行张力为导线计算拉断力的20%,风暴中心分别垂直于3号、4号和5号绝缘子及第三、第四档档距中央,并改变风暴中心到线路的垂直距离,提取各计算工况下绝缘子串底部导线挂点处的X向位移,(X向位移为垂直于线路走向方向的位移,如图9所示,即绝缘子串风偏角形成的三角形底边长度)讨论各绝缘子串最大风偏位移与风暴中心的位置关系。计算风偏角并给出各绝缘子串风偏角随风暴中心位置变化的规律曲线图。在图9中:dp为射流中心到线路的垂直距离;Djet为射流直径;Ppe为射流中心在水平投影面的投影点。
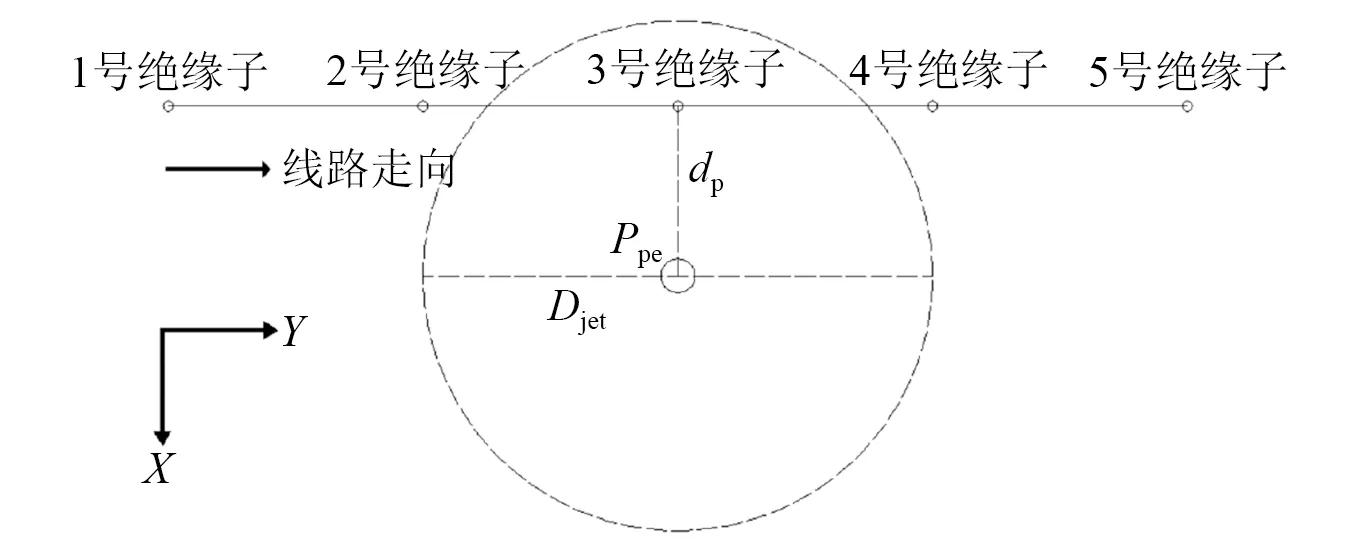
图9 风暴中心与线路位置示意图Fig.9 Schematic diagram of calculation conditions
3.3.2 风偏响应分析
由于线路档距均匀且下击暴流风场是三维对称风场,选取3号绝缘子作为代表分析。表3为3号绝缘子在不同工况下的风偏角最大值。
风暴中心位置改变时各绝缘子串风偏角的变化规律图,如图10所示。
由图10可知,射流中心与线路垂直距离不变的情况下,目标绝缘子与射流中心的水平距离越近,目标绝缘子风偏角越大。而随着射流中心与线路垂直距离的增大,目标绝缘子的风偏角是先增大后减小的。当在射流中心垂直目标绝缘子且射流中心距线路垂直距离为1.25倍射流直径时,目标绝缘子风偏角达到最大值,以3号绝缘子为例,最大风偏角为56.541 9°。这与风场径向风速的最大值产生在r=1.25Djet处的结果是相吻合的,也说明了输电线路风偏有限元分析的正确性。
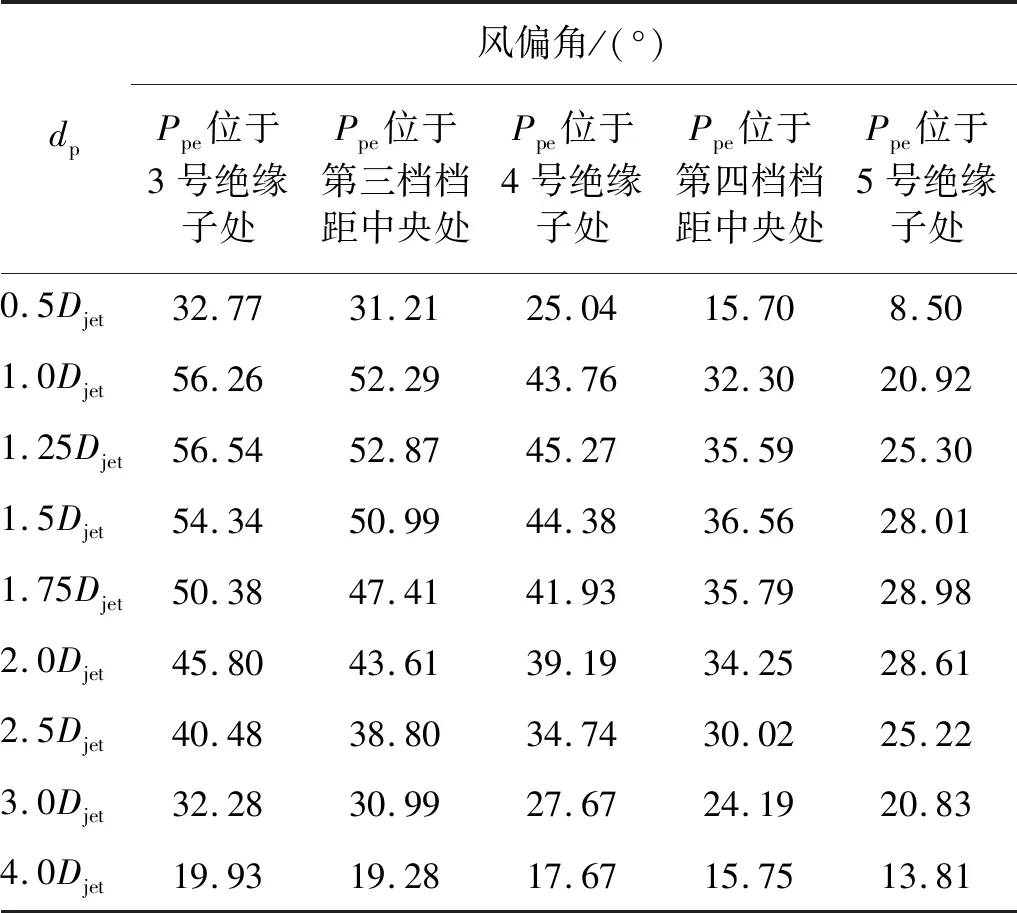
表3 3号绝缘子风偏角最大值Tab.3 Finite element wind deflection results of No.3 insulator
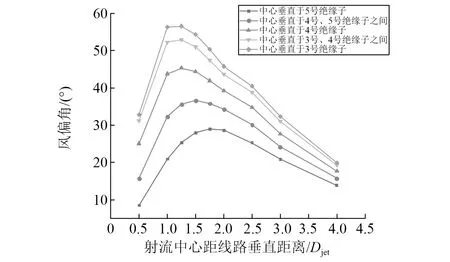
图10 风暴中心位置变化时3号绝缘子串风偏角Fig.10 Effect of storm center position on wind deflection of insulator string
3.4 线路档距和运行张力变化对风偏影响
本文档距变化为400 m~600 m,档距增量为50 m。导线张力变化为17.5%~25.0%导线计算拉断力,射流倾角分别为0°,10°和20°,风暴中心垂直于3号绝缘子且垂直距离为1.25Djet,分别计算得出3号绝缘子串的风偏角,图11给出了3号绝缘子风偏角随档距变化的规律曲线。
由图11可知,最不利工况为在射流倾角为0°、导线张力为17.5%导线计算拉断力、档距为550 m时,3号绝缘子的最大风偏角为57.18°;在三种风场中,当其他因素不变时,随着输电线路档距的增加,绝缘子串风偏角逐渐变大。但随着档距的增加,风偏角随着档距增大而增大的趋势逐渐变缓,且在射流倾角为0°和20°、线路档距改变为550 m~600 m时,导线张力较小工况下绝缘子串风偏角呈下降趋势。
在档距为400 m处的倾角为20°的风场中的风偏角大于倾角为0°的风偏角,而档距为600 m处又小于倾角为0°的风偏角。故当导线张力较大时,档距在400 m~500 m,在倾角为20°的风场中,线路发生风偏闪络事故的可能性更大;档距在500 m~600 m,在倾角为0°的风场中,线路发生风偏闪络事故的可能性更大。
不同风场下3号绝缘子风偏角随导线张力变化的规律,如图12所示。
由图12可知,在3种射流倾角下,当其他条件不变时,随着导线张力的增加,绝缘子串风偏角逐渐变小。但随着导线张力的增加,风偏角随着导线张力增大而减小的趋势逐渐变缓 ,且在风场倾角为0°和20°时,在线路档距为550 m和600 m、导线张力较小时绝缘子串风偏角基本保持不变。其中由于档距为600 m、导线张力为15%导线计算拉断力工况的档距中央导线弧垂过大,导线最低点距离地面过近。不符合实际,没有讨论意义。故舍去此种工况。

图11 档距变化对风偏角影响Fig.11 Influence of span change on wind deflection angle
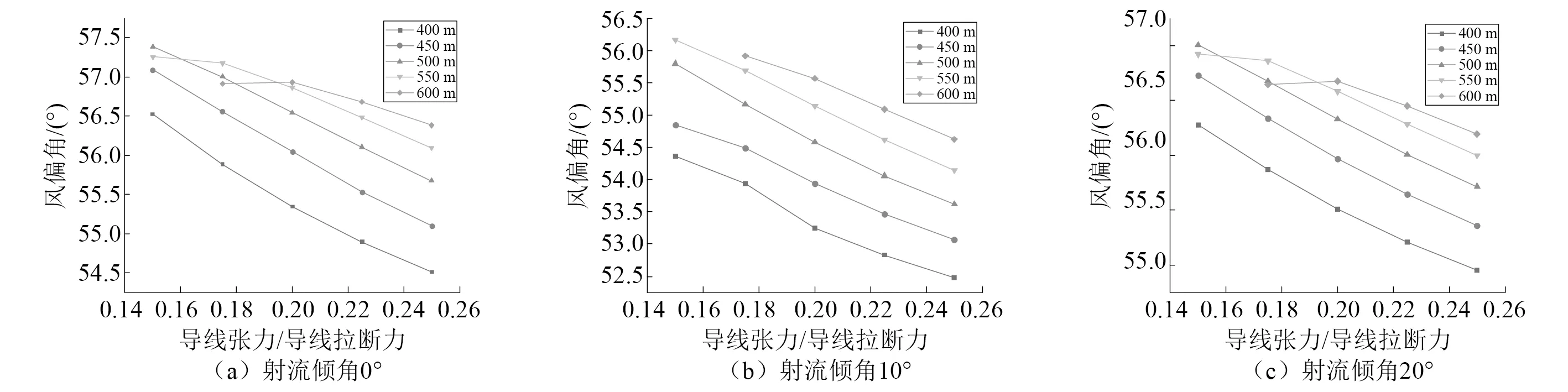
图12 导线张力变化对风偏角影响Fig.12 Influence of conductor tension variation on wind deflection angle
3.5 档距中央导线风偏位移分析
对于输电线路而言,不仅要关注绝缘子串悬挂导线处的风偏,也要关注档距中央导线的风偏,下面给出档距中央导线风偏位移的计算结果。风暴中心分别垂直于第3、第4档距中央、垂直距离为1.25Djet时档距中央导线风偏位移对比图,如图13所示。同样工况下图14和图15分别给出了线路档距和导线运行张力变化时第3档档距中央导线风偏位移响应。
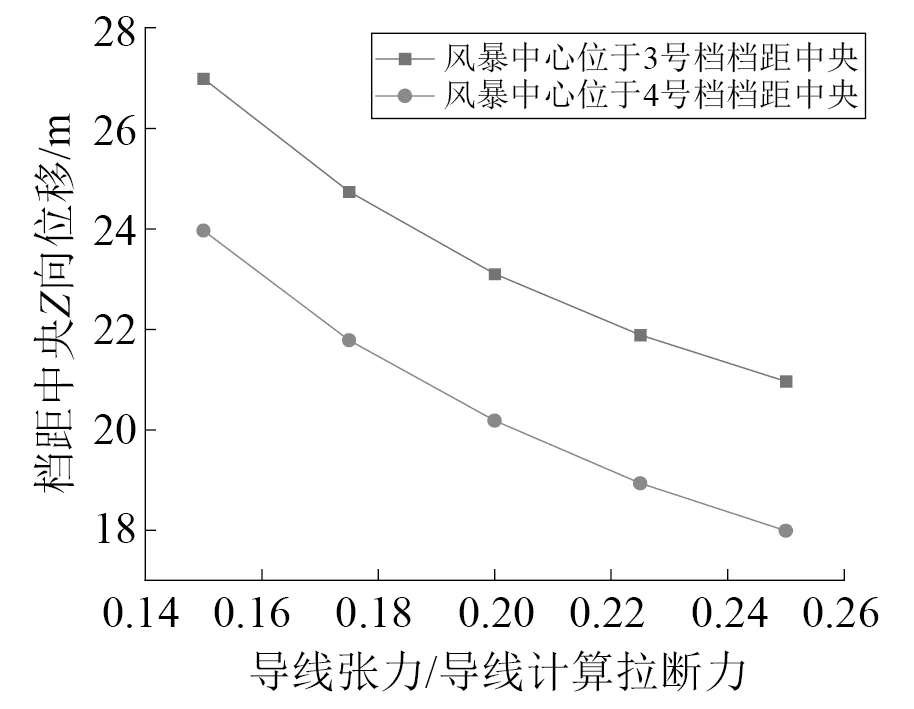
图13 风暴中心不同位置时档距中央导线风偏位移Fig.13 Comparison of wind deflection of span central conductor
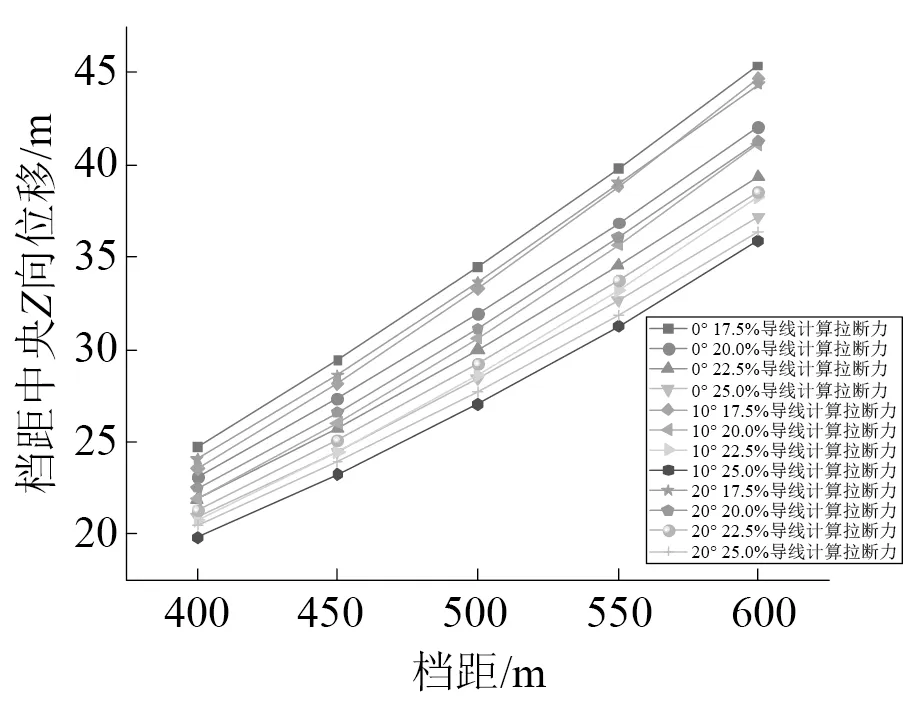
图14 导线风偏位移随档距变化Fig.14 Variation of wind deflection displacement of conductor with span
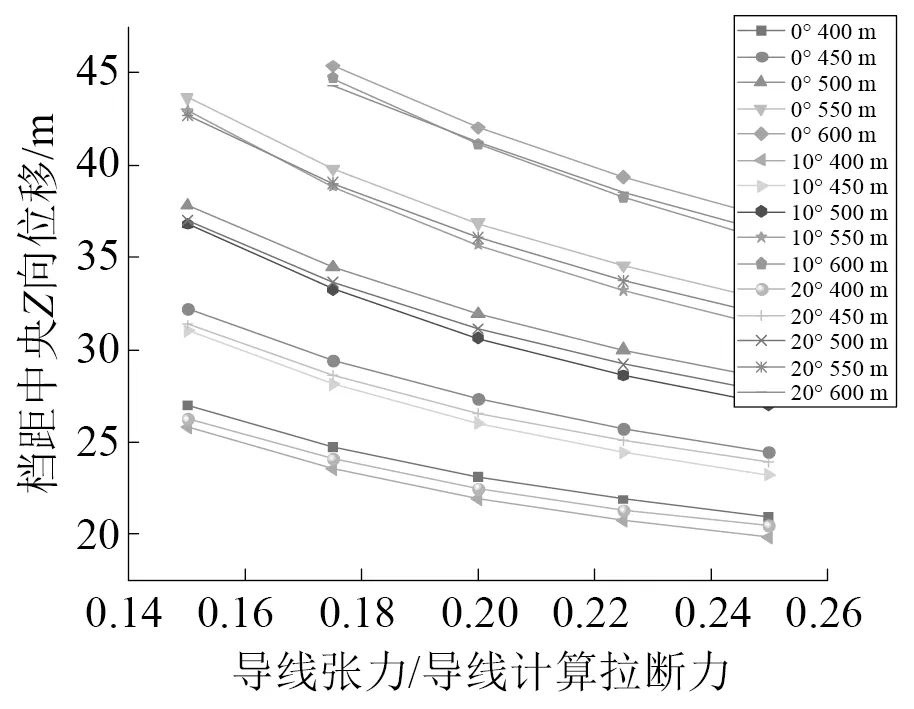
图15 导线风偏位移随导线张力变化Fig.15 Variation of wind deflection displacement of conductor with conductor tension
由图13可知,当将风暴中心置于第三档档距中央时,档距中央导线的风偏位移(为档距中央处导线垂直于线路走向方向的位移,即X方向的位移)明显大于风暴中心位于第四档档距中央的情况。
由图14可知,三种风场下档距中央导线风偏位移都是随着档距的增加而增大,三种风场中风偏位移的大小分别是倾角为0°的最大,倾角为20°的其次,倾角为10°的最小。最大的档距中央风偏位移发生在风场倾角为0°、档距为600 m、导线张力为17.5%导线计算拉断力时,最大的档距中央风偏位移达到了45.36 m,其他因素不变的情况下,档距为400 m的档距中央风偏位移仅为24.74 m,两者相差了20.62 m,可见档距变化对档距中央导线风偏位移的影响极大,在线路设计时要充分的考虑线路周围的地形因素,防止导线风偏对周围物体放电。
由图15可知,三种风场下档距中央的导线风偏位移随着导线张力的增加而减小,但随着导线张力的增加。风偏位移减小的趋势变缓,最大的风偏位移同样是发生在风场倾角为0°、档距为600 m、导线张力为17.5%导线计算拉断力时,最大的风偏位移为45.36 m,在其他因素不变的情况下,当导线张力增加到25%导线计算拉断力时,导线风偏位移为37.2 m,减小了8.16 m,相对于档距变化减小的20.62 m来说,导线张力变化对档距中央导线风偏位移的影响较小,不到档距变化带来的影响的一半,因此在实际线路设计中可以着重考虑缩小档距,防止线路档距中央导线风偏位移过大带来的风偏闪络危险。
3.6 输电线路风偏响应时程分析
下击暴流可分为生成阶段、下沉阶段、冲击阶段和扩散阶段,考虑到三维下击暴流风场和线路在空间上的对称特性,本节以档距为400 m,导线张力为导线计算拉断力的17.5%,风暴中心垂直于3号绝缘子,垂直距离为1Djet的工况为例分析。分析线路3号绝缘子在下击暴流各个阶段时的风偏响应特征,风偏位移随时间变化的规律,得出最大风偏角,将得出的最大风偏角θ1与稳定后的风偏角θ2对比,得出绝缘子串在下击暴流冲击地面加速阶段的风偏角增大百分比η,见式(5)。导线上各点风速时程曲线,如图16所示。3号绝缘子底端风偏位移时程曲线,如图17所示。
η=(θ1-θ2)/θ2
(5)
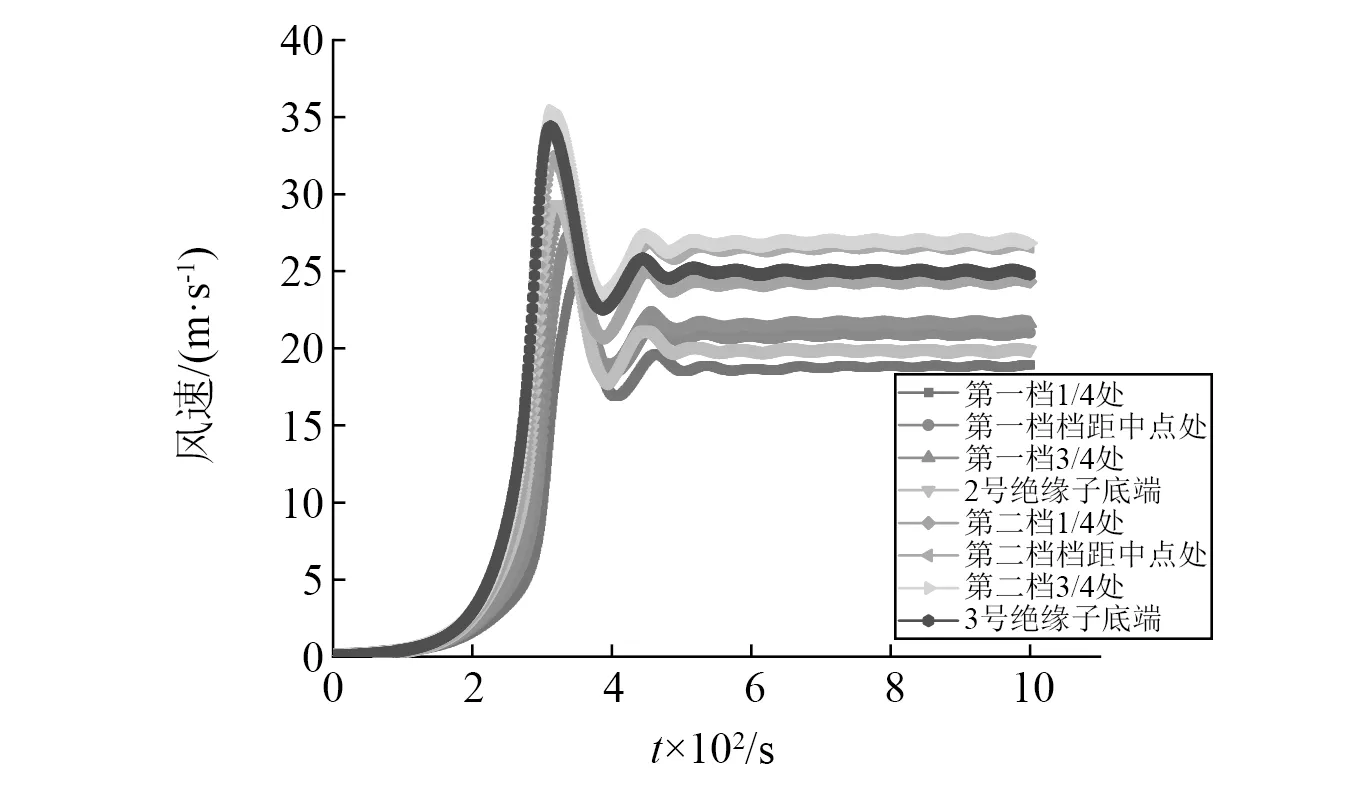
图16 导线上各点的风速时程曲线Fig.16 Wind speed time history curve of each point on the conductor
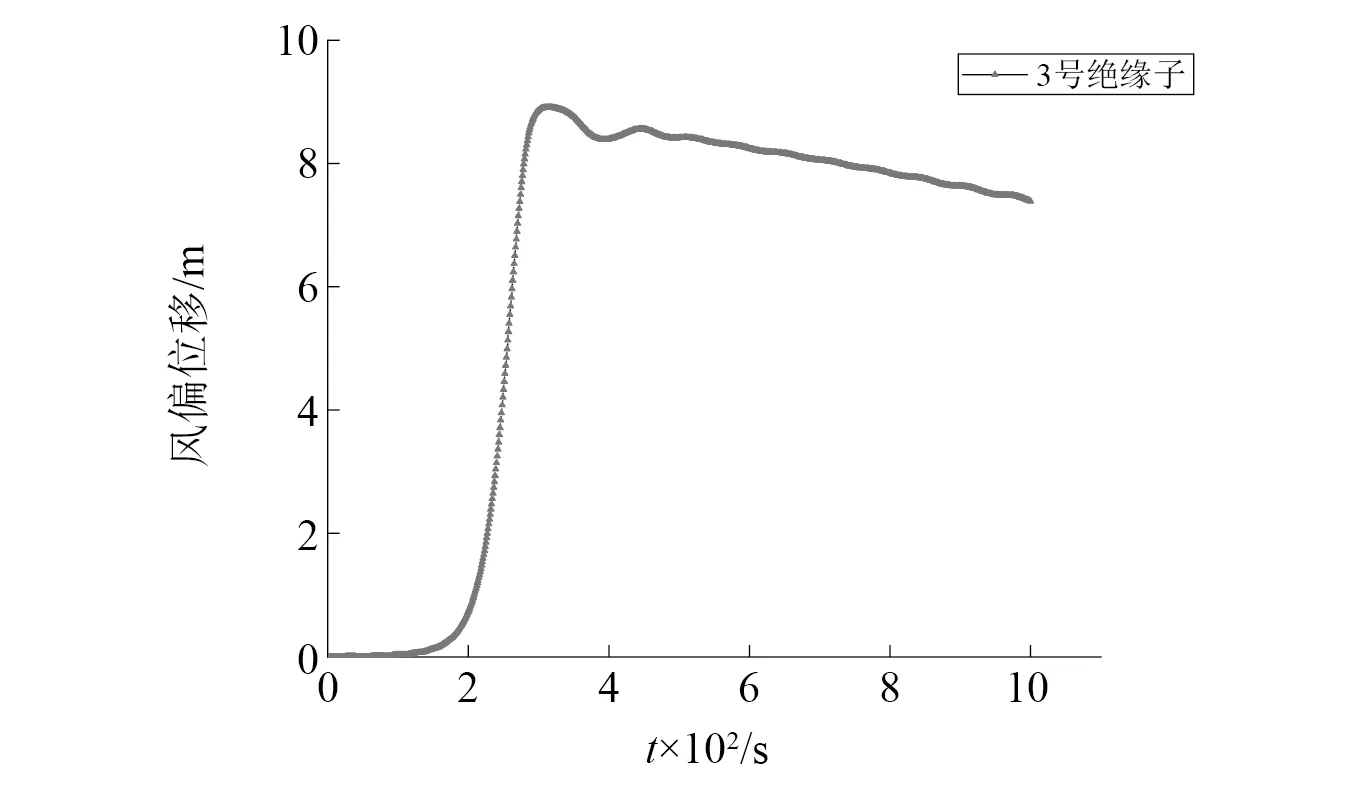
图17 绝缘子串风偏位移时程曲线Fig.17 Time history curve of wind deflection displacement of insulator string
由图16可知,导线上各点的风速随着时间的变化的规律基本相同,大致可分为3个阶段,与风场的瞬态特征相对应。
(1) 此阶段风速从0迅速增至最大值,此阶段与风场瞬态特征中的下沉与冲击地面加速阶段相对应,下沉气流冲击地面产生漩涡,旋涡向线路方向移动,导线上各点风速迅速增加,并且在漩涡到达线路处时达到最大值。
(2) 此阶段风速由最大值开始下降并达到整个时间历程中的最小值,与风场瞬态特征中扩散阶段的前期相对应。此时漩涡经过导线开始向远处扩散,由于漩涡离开导致能量损耗,该位置近地面风速持续降低,导线上各点风速迅速减小,达到最小值。
(3) 此阶段风速由最小值开始略微增加直至稳定,在稳定后只有微小的波动,对应风场瞬态特征中扩散阶段的后期。由于漩涡的远离并且开始脱落,此时漩涡对导线上各点风速没有影响,又因射流口能量的持续输入,线路位置处的风速开始逐渐增大直到到稳定。并且由总体的风速时程曲线可看出,风速无论是的增大还是减小,所用的时间都较短,在整个下击暴流生命周期内,风速平稳的阶段占据了绝大部分。
由图17可知,3号绝缘子串的风偏位移时程大致也可分为3个阶段与上述相对应,略有不同的是当风速稳定后绝缘子的风偏位移是近似成线性下降的。3号绝缘子的最大风偏位移为8.91 m,风偏角为81.97°,发生在311 s,也就是下击暴流的冲击地面加速阶段,随后逐渐下降,在风速平稳阶段的风偏位移由计算结果得为7.396 8 m,风偏角为55.27°,经计算风偏角增大百分比η=48.3%。可见在下击暴流的冲击地面加速阶段,由于极大的风荷载以及风速迅速增加产生的动力响应导致线路绝缘子的风偏角极大,约为风速平稳阶段的1.5倍,极易发生风偏闪络事故,但持续时间较短,随着漩涡的远离,风速迅速下降,绝缘子串的风偏角也逐渐减小。
4 结 论
(1) 在射流倾角α分别为0°,10°和20°风场中,径向风速最大值都发生在r=1.25Djet处。风场中的极值风速随着倾角的增加反而略微减小,并且随倾角α的增大,径向风速随高度增加而减小速率变缓,极值风速所维持的高度区间变小。
(2) 随着射流中心与线路垂直距离的增大,绝缘子的风偏角是先增大后减小的,垂直距离为1.25Djet时,目标绝缘子风偏角达到最大值,并且绝缘子与射流中心的水平距离越近,绝缘子风偏角增大和减小速度越快。
(3) 在三种射流倾角风场中,绝缘子串风偏角和档距中央导线风偏位移都是随着输电线路档距的增加逐渐变大的;都是随着导线张力的增加逐渐变小的,但对于档距中央导线风偏位移来说导线张力的变化相对于档距变化带来影响是有限的,在实际线路设计中应着重考虑档距的变化带来的影响。
(4) 由于射流倾角较大风场的极值风速比较小风场的小,且风速沿高度变化下降的较慢,所以在导线平均高度较低的情况下,在倾角小的风场中发生风偏闪络的可能性更大;在导线平均高度较高的情况下,在倾角大的风场中发生风偏闪络的可能性更大。
(5) 在下击暴流作用下,绝缘子串风偏位移是先迅速增到最大值再近似呈线性下降直至稳定,风偏角的最大值约为稳定后风偏角的1.5倍。
