整体螺栓滚轮滚针轴承滚子素线优化设计研究
2022-09-17姜艳红丁士钊张剑李鑫斌刘静
姜艳红,丁士钊,张剑,李鑫斌,刘静
(1.中浙高铁轴承有限公司,浙江衢州 324400;2.重庆大学机械工程学院,重庆 400044;3.西北工业大学航海学院,陕西西安 710072;4.西北工业大学,无人水下运载技术工业和信息化部重点实验室,陕西西安 710072)
0 前言
整体螺栓滚轮滚针轴承在航空航天领域得到了广泛应用,但是该轴承在工作过程中需要灵活回转,因此需要合适的轴向间隙,同时为了提高轴承径向承载能力,应设计合理的滚针表面型线。圆柱形滚子边缘的应力集中会使轴承的工作精度和工作寿命都大幅度下降。因此,开展滚子素线优化设计研究能够为提高滚轮滚针轴承的承载能力提供参考。
目前,许多学者在滚动轴承滚子修形方式方面开展了大量的研究工作。陈亚军等分析了大挡边形状对圆锥滚子轴承接触应力和疲劳寿命的影响规律。吴正海等建立了圆锥轴承滚子与滚道接触的非等温脂润滑模型,分析了滚子修形、打滑、歪斜和倾斜等对接触副脂润滑热成膜性能和拖动性能的影响规律。吴继强等综合考虑轴承接触工况、滚子修形参数和真实表面粗糙度等因素的影响,建立了圆柱滚子轴承混合润滑数学模型,分析了滚子修形参数和转速对轴承润滑性能的影响规律。鄢闯和杨霞建立了不同修形曲线的圆柱滚子轴承有限元模型,分析了外圈剥落缺陷对轴承振动特性的影响规律。魏延刚等基于轴承载荷离散分布模型的计算方法,采用对数修形曲线进行对称修形,分析了圆锥滚子的最大接触应力沿其母线的分布规律;采用有限元方法研究了圆柱滚子轴承滚子的凸度修形量对接触应力和等效应力的影响规律。李海涛等应用有限元分析方法分析了直母线圆锥滚子轴承端部存在的应力集中现象,并研究了滚子母线对数修形的载荷适应性。KOUNTANYA和JAGDALE提出了凸度圆柱滚子的赫兹无摩擦弹性接触公式。何培瑜等分析了纯径向力工况、中心偏载工况和偏中心倾斜工况下对数修形滚子对转盘轴承应力分布的影响规律。
虽然许多学者已经对圆柱滚子和圆锥滚子轴承滚子的修形方式进行了大量研究,但是对滚轮滚针轴承滚子修形方式对接触变形和接触应力分布影响的研究较少。针对这一问题,运用非理想赫兹接触理论,建立整体螺栓滚轮滚针轴承滚子与滚道非理想赫兹接触模型,研究全圆弧母线修形、相交圆弧母线修形、相切圆弧母线修形和对数母线修形方式对滚子与滚道之间接触变形和应力分布的影响规律。研究结果可为滚轮滚针轴承滚子修形方式的优化设计提供参考。
1 滚轮滚针轴承结构特征与载荷分析
滚轮滚针轴承为满装圆柱滚子轴承,其外圈可以直接在滚道上滚动,并可以承受较重负荷和冲击负荷。滚轮滚针轴承的结构简图如图1所示,其中:左端是为滚针轴承;轴承外圈在外部滚道上面滚动;右端通过螺纹连接固定,轴承螺栓承受径向载荷。在径向载荷作用下,螺栓会引起滚子发生偏斜,影响滚子与内外滚道之间的接触变形和接触应力,从而影响轴承的工作特性和疲劳寿命。对滚轮滚针轴承的滚子素线进行优化设计可有效改善滚子与滚道之间的接触特性,从而改善轴承的工作特性和提高轴承的疲劳寿命。

图1 滚轮滚针轴承剖面简图
根据滚轮滚针轴承的安装条件,该轴承可近似为一个悬臂梁结构,如图2所示。
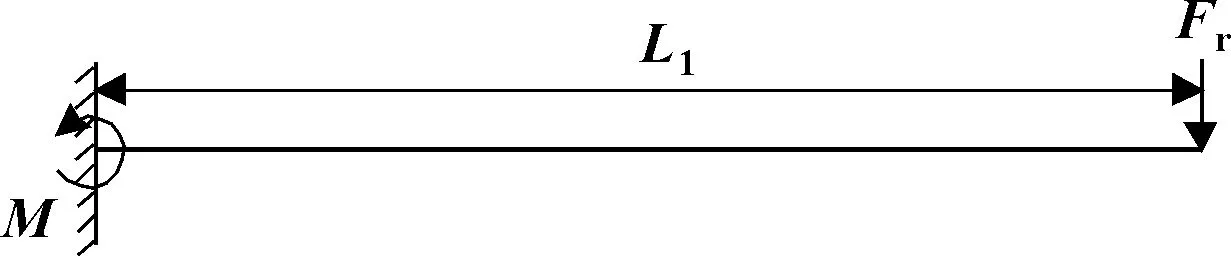
图2 滚轮滚针轴承受力示意
根据载荷平衡条件,轴承两端支点载荷的关系式为
=
(1)
式中:为轴承的径向载荷。轴承单个滚子的最大载荷表示为

(2)
式中:为滚子最大载荷;为滚子数;为初始接触角,其取值为=0°。
2 非理想赫兹接触算法
滚轮滚针轴承滚子长度通常都小于滚道宽度,滚针素线一般存在修形(图1所示),滚子与滚道之间的接触问题已经超出理想赫兹线接触理论的范围。该类问题可采用非理想赫兹接触理论进行计算。非理想赫兹接触算法的基本方程为
∬(,)dd=
(3)
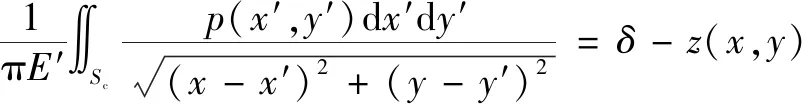
(4)
式中:为两接触体的接触区域;(,)为接触区域内的接触应力;为径向载荷;为接触变形;(、)为两接触体的初始间距。该算法中假定将接触表面划分为×的矩形单元,每一个单元的中心为一个节点,并假设每一个单元内的接触应力为常数。各单元的柔度系数为

(5)
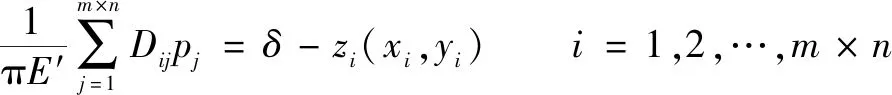
(6)
该算法计算过程:设定变形量的初值,若计算过程中小于0,说明该区域两接触体已经分离,下次迭代计算则不考虑此单元。通过改变的值,可利用式(5)和(6)迭代计算滚子与滚道的非理想线接触的接触应力与变形,直至值在误差范围内为止。具体计算方法参见文献[11]。
3 滚子修形方式
参考典型滚针滚子轴承的修形方式,文中选取的滚轮滚针轴承滚子素线的修形方式包括全圆弧母线、相交圆弧母线、相切圆弧母线和对数母线,如图3所示。
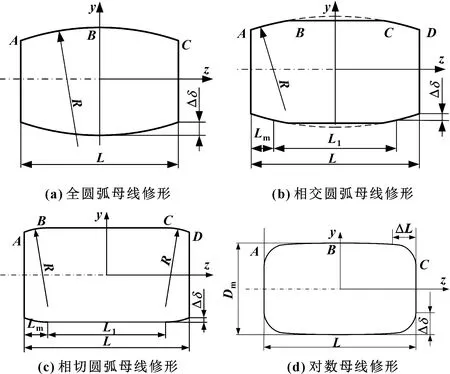
图3 滚子修形方式
3.1 全圆弧母线修形
全圆弧母线修形的素线是整段圆弧,如图3(a)所示,其修形量为

(7)
式中:为弹性模量;为泊松比;为滚针接触长度;为设计载荷。图3(a)中,曲线半径和的计算公式为
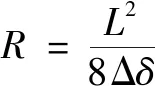
(8)
该滚子素线在向的方程为

(9)
3.2 相交圆弧母线修形
相交母线修形的滚子形状如图3(b)所示,该滚子素线包括两条曲线和及一条直线,其修形量公式与式(7)相同。曲线半径和的计算公式为
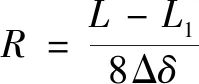
(10)
其中:未修形部分的滚子长度的公式为
=07
(11)
修形部分的滚子长度为
=015
(12)
该滚子素线相对于轴的方程为
=
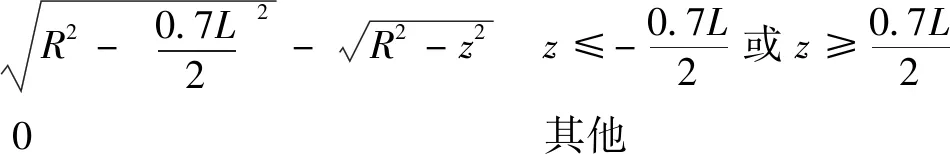
(13)
3.3 相切圆弧滚子修形
相切母线修形的滚子形状如图3(c)所示,该滚子素线包括两条曲线和及一条直线,其修形量公式与式(7)相同。曲线半径和的计算公式为

(14)
该滚子素线相对于轴的方程为
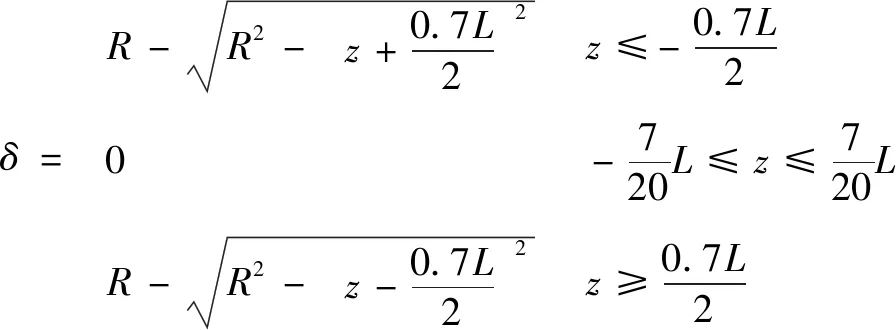
(15)
3.4 对数母线修形
对数母线修形的滚子形状如图3(d)所示,该滚子素线包括两条曲线和,其修形量公式与式(7)相同。
该滚子和滚道之间的接触宽度为
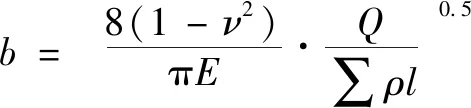
(16)
滚道和滚子之间的综合曲率半径为

(17)
式中:为圆柱滚子轴承节圆直径;为滚动体有效直径。该对数母线修形素线方程为
=
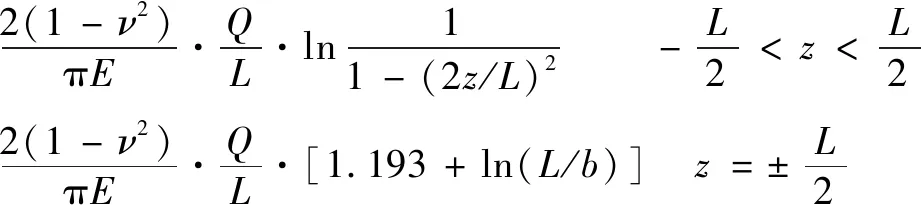
(18)
4 仿真结果与分析
选取滚轮滚针轴承KRV30为研究对象,其主要尺寸参数如表1所示。
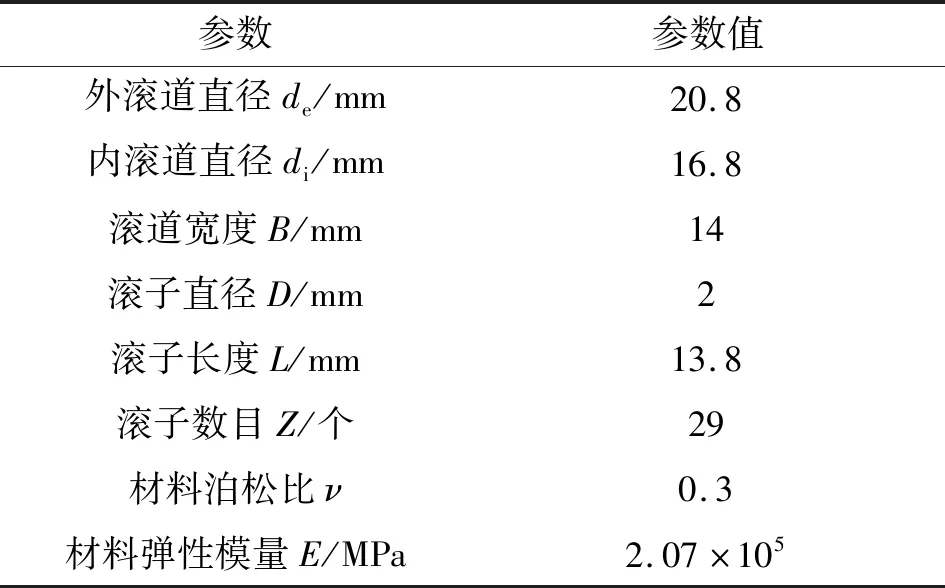
表1 滚轮滚针轴承KRV30主要参数
4.1 滚子修形方式对滚子与滚道之间接触变形的影响规律
当许用载荷为11 000 N时,利用公式(1)和(2)计算获得的滚轮滚针轴承滚子最大载荷为1 547 N。运用非理想赫兹接触理论计算方法,得到4种不同修形方式对滚子与滚道之间接触变形的影响规律如图4所示。可知:滚子径向接触变形随着径向压力的增加而增加;相同载荷下,相切圆弧母线修形滚子的接触变形最小,全圆弧母线修形滚子的接触变形最大;对数母线修形滚子的接触变形与相切圆弧母线修形滚子和相交圆弧母线修形的滚子的接触变形量相近。

图4 滚子修形方式对滚子与滚道之间接触变形的影响规律
4.2 滚子修形方式对滚子与滚道之间接触应力分布的影响规律
滚子修形会改变滚子的应力分布,减少应力集中现象,改善工作状况,增加工作寿命。图5—图8分别为全圆弧修形、相交圆弧母线修形、相切圆弧母线修形和对数凸度修形滚子的接触应力分布规律。可知:相交圆弧母线修形和相切圆弧母线修形滚子存在接触应力集中现象;全圆弧母线修形和对数母线修形的接触应力分布均匀;对数母线修形滚子的接触应力最小;随着径向载荷增大,滚子与滚道之间接触应力随之增大。结果表明,对数母线修形是更合适的滚轮滚针轴承滚子素线的修形方式。
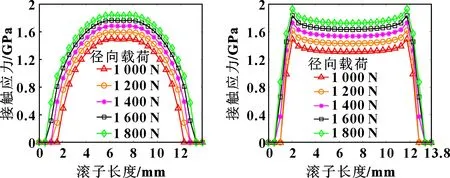
图5 全圆弧母线修形滚 图6 相交圆弧母线修形滚
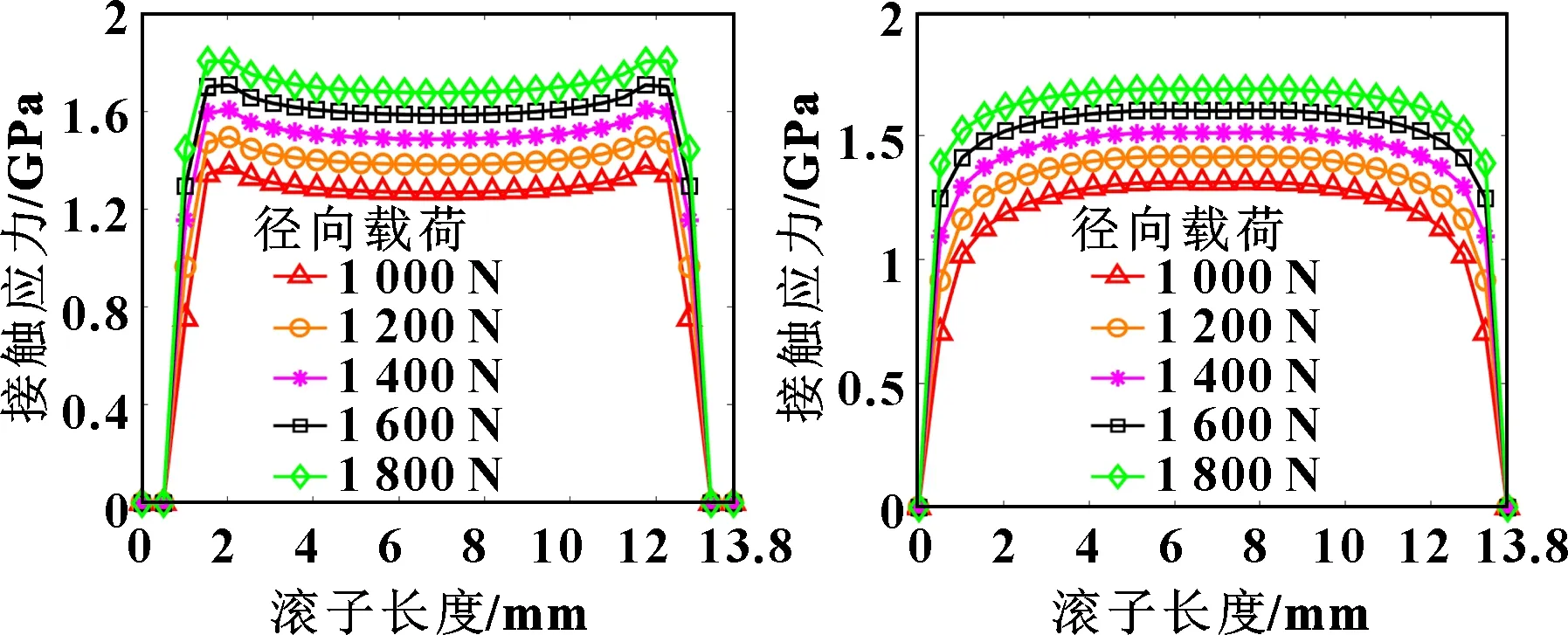
图7 相切圆弧母线修形滚 图8 对数母线修形滚子
4.3 滚子偏斜对对数母线修形滚子接触变形和接触应力的影响规律
由图4—图8可知对数母线修形相对于其他3种修形方式更合适于滚轮滚针轴承滚子修形。因此,选取的滚子修形方式为对数母线修形,分析滚子偏斜对其接触变形和接触应力的影响规律。图9所示为滚子偏斜对对数母线修形滚子接触变形的影响规律。可知:相同径向载荷情况下,滚子偏斜会增大对数母线修形滚子的接触变形量。图10所示为滚子偏斜对对数母线修形滚子接触应力的影响规律。可知:滚子存在偏斜时,对数凸度修形滚子在滚子素线上的一端有很大的应力,在滚子素线上接触应力依然分布均匀。
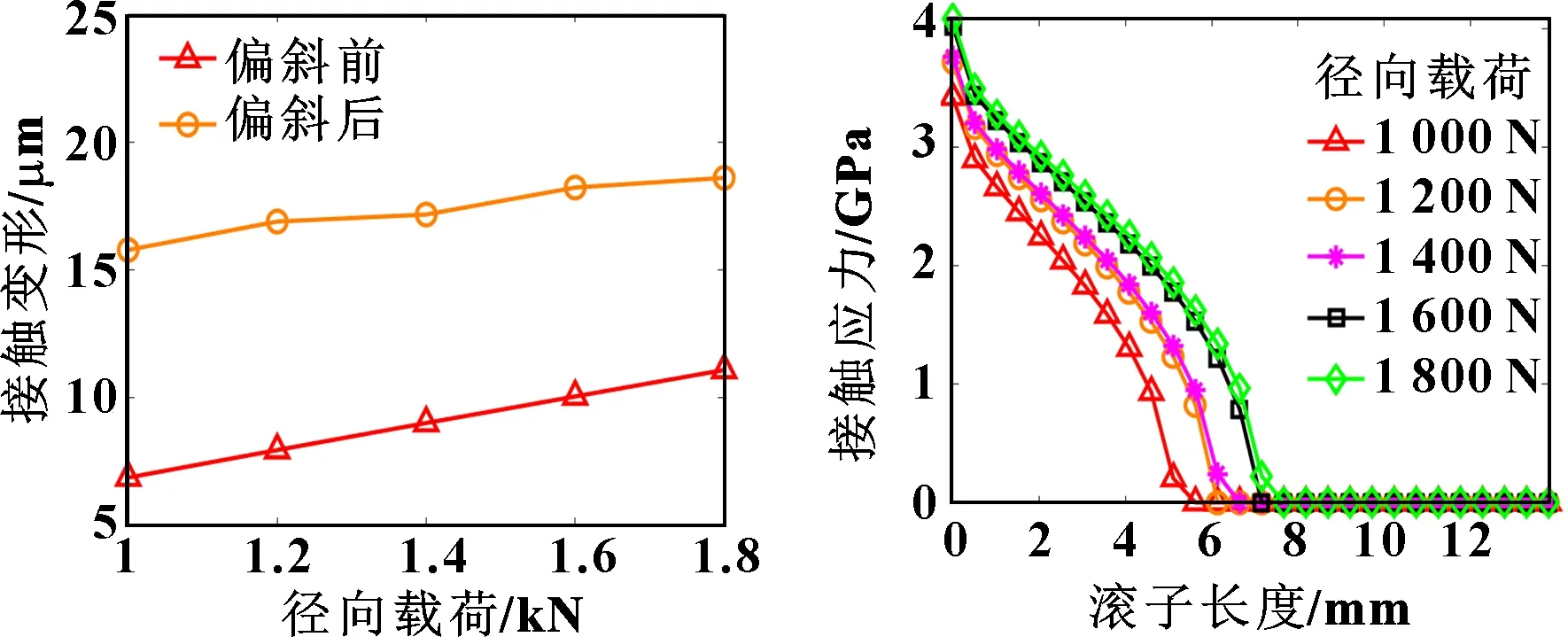
图9 对数母线修形 图10 滚子偏斜对对数母
5 结论
本文作者运用非理想赫兹接触理论,建立了整体螺栓滚轮滚针轴承滚子与滚道非理想赫兹接触模型,分析了全圆弧母线、相交圆弧母线、相切圆弧母线和对数母线4种修形方式对滚轮滚针轴承滚子与滚道之间的接触变形和接触应力分布的影响规律。结果表明,滚子修形对滚子与滚道之间的接触变形和接触应力有较大的影响。主要结论如下:
(1)滚子径向接触变形随着径向载荷的增加而增加;相同载荷的情况下,相切圆弧母线修形的滚子接触变形最小,全圆弧母线修形滚子的接触变形最大;对数母线修形滚子的接触变形与相切圆弧母线修形滚子和相交圆弧母线修形的滚子的接触变形量相近。
(2)相交圆弧母线修形和相切圆弧母线修形滚子存在接触应力集中现象;全圆弧母线修形和对数母线修形的接触应力分布均匀;对数母线修形滚子的接触应力最小。
(3)相同径向载荷情况下,滚子偏斜会增大对数母线修形滚子的接触变形量;滚子存在偏斜时,对数凸度修形滚子在滚子素线的一端有很大的应力,在滚子素线上接触应力依然分布均匀。
(4)相对于其余3种滚子修形方式,对数母线修形是更合适的滚轮滚针轴承滚子素线修形方式。
