基于改进阈值估计和改进阈值函数的局部放电信号降噪方法
2022-12-01刘志坚赵浩益罗灵琳李鹏程
刘志坚,赵浩益,刘 航,罗灵琳,宋 琪,李鹏程
(昆明理工大学 电力工程学院,昆明 650500)
超声波检测是一种经典的高压电力设备局部放电故障源定位和类型识别的基础方法,对于维护电力系统运行稳定性和安全性有重要意义[1-2]。然而运行经验表明,现场工作环境中存在大量以白噪声、电磁噪声为代表的干扰源,造成局放信号的污染甚至淹没。因此,如何准确、完整地提取原始超声波信号,最大程度地抑制干扰成为局部放电监测的关键内容[3-5]。
小波变换方法具有多频段分离、多分辨率分解的能力,在非平稳信号降噪处理中体现出较好的优势而得到广泛应用[6-7]。基于小波阈值的降噪方法基本步骤包括:①对原始信号进行小波分解;②对分解后的各系数组分进行降噪处理;③将处理后的各低噪系数组分重构,获得降噪后的原始信号[8]。在步骤②中,阈值优化估计及阈值函数的选择和设计是影响降噪效果的重要因素,现有的研究大多围绕上述两个关键内容来展开。
在阈值优化估计方面:文献[9-11]构造了含阈值梯度的适应度函数,并基于启发式算法搜索最优阈值,克服了降噪适应度函数对于标准信号的先验依赖,为实现阈值梯度构造,此方法要求阈值函数在阈值邻域内具有连续可导性,所以对于不连续、不可导的阈值函数不具备适应性;文献[12-15]将时间序列样本熵理论引入阈值估计中,以估计噪声序列复杂度为依据,选取噪声序列最大样本熵值下的阈值作为最优阈值估计值。然而,这种阈值估计方法存在两方面局限性:①最大样本熵指标不能完整描述原始信号中全部噪声的集合,最大样本熵下估计的阈值存在偏小风险,使信号降噪不完全;②不同阈值步长下样本熵极值的搜索精度和搜索速度存在矛盾性,估计的阈值容易陷入局部解。针对局限性①,目前鲜有相关研究和解决办法;针对局限性②,有研究考虑采用启发式算法优化最大样本熵,避免人为选择步长对寻优误差的影响,但其基本原理仍然是基于最大样本熵的阈值估计,并没有克服局限性①带来的问题。
在阈值函数改进方面:文献[16]构建了一种在阈值处连续且可导的阈值函数,以改进传统阈值函数存在的重构偏差和过度降噪缺陷;文献[17-19]提出介于软、硬阈值之间的连续阈值函数。上述提出的各种阈值函数改进形式不同,但均可以通过调整函数携带的参数在不同程度上实现对软、硬阈值函数缺陷的改善,达到提升降噪效果的目的,但是存在着参数选择讨论不充分、函数临界阈值处不可导、系数处理过渡不平滑的情况,在一定程度上影响了重构信号的质量。
在上述研究的基础上,提出一种基于快速综合熵和改进阈值函数的局部放电信号小波降噪方法。首先,建立了融合噪声序列样本熵和降噪序列样本熵的综合熵模型,使用二分变步长迭代方法实现了最优阈值的快速估计;进而,提出一种融合软、硬阈值特征的新型阈值函数,该函数的连续平滑过渡特征能够有效抑制原始信号的重构振荡和重构偏差;最后,使用多个高压电力设备局部放电超声波脉冲信号开展仿真和测试,对本文所提降噪方法的有效性进行了验证。
1 局部放电超声波模型及小波降噪基本流程
1.1 局部放电超声波信号数学模型
电力设备长期运行在高压电磁环境下,随着工作时间的增加,当设备绝缘出现局部缺陷时,会在该区域产生伴随声、光放射的放电现象,称为局部放电(partial discharge,PD),简称局放。局放源属于点源,其产生的超声波信号以简谐波的形式向周围环境辐射,常见的局放超声波信号数学模型如式(1)所示[20]
(1)
式中:A0为幅值;t0为初始时间;τ为衰减常数;f为衰减振荡频率。
根据式(1)模型,标准的局放超声波时域仿真信号如图1(a)所示,可见局放超声波是一种高频振荡的衰减信号,运行环境中产生的局放超声波信号往往会受到各种噪声干扰,含噪的超声波脉冲时域仿真信号如图1(b)所示。实际上,在带绝缘缺陷的电力设备运行中,并不是仅仅产生一次局放现象,而是在同一局放源处会以一定的时间间隔周期性地发生局部放电,时域仿真信号如图1(c)所示。
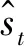
(2)

图1 局部放电超声波信号模型Fig.1 Model of partial discharge ultrasonic signal
1.2 基于小波理论的局放超声波信号降噪过程
基于小波阈值的信号降噪基本过程如下:
步骤1小波分解——选择合适的小波基与分解层数对原始信号进行尺度分解,得到各频段的小波系数;
步骤2系数处理——确定系数处理的阈值,通过阈值函数对高频小波系数去噪处理得到降噪系数;
步骤3信号重构——基于步骤2得到的降噪系数与低频系数完成信号重组,实现信号降噪。
其中,步骤2的阈值选取和阈值函数设计反映了系数处理的映射规则,会对降噪质量产生重要影响,是小波阈值去噪的重要环节,本文从最优阈值估计和阈值函数改进两个方面实现对传统阈值函数降噪方法的优化。
2 基于综合熵的最优阈值估计方法
2.1 基于样本熵的阈值估计基本原理及不足
2.1.1 样本熵基本理论及阈值估计应用
(1) 样本熵基本理论
样本熵通过计算一维时间序列中新模式的生成概率来反映序列混乱度,由于具有良好的噪声序列复杂度表征能力而被广泛引入到阈值估计中,针对长度为N的信号序列Xi={x1,x2,…,xN},其样本熵值计算过程如下:
步骤1设定嵌入维数m和相似容限r,考虑维数为m的向量组{xm(1),…,xm(N-m-1)},其中
Xm(i)={x(i),x(i+1),…,x(i+m-1)}
(3)
步骤2设两个向量Xm(i)和Xm(j)之间的距离d[Xm(i),Xm(j)]为向量之间对应元素之差绝对值的最大值,其表达式为

(4)
步骤3设定固定的Xm(i),对Xm(i)和Xm(j)之间的距离小于等于相似容限r的数目j(1≤i≤N-m,j≠i)进行统计,并记作Bi,定义两个向量在相似容限下匹配m个点的概率,记作Bm(r),其表达式为
(5)
(6)
步骤4将嵌入维数增加到m+1,按照上述计算Xm+1(i)与Xm+1(j)之间的距离小于等于相似容限r的数目j(1≤i≤N-m,j≠i)进行统计,记为Ai,定义两个向量在相似容限下匹配m+1个点的概率,记作Am(r),其表达式为
(7)
(8)
步骤5定义序列样本熵(sample entropy,SE)为
(9)
实际信号中N通常为有限值,样本熵估计为
(10)
根据上述步骤,样本熵的计算与参数m,r取值有关,在实际应用中,一般取m=1或m=2,r=0.1std(X)~0.25std(X),std(X)为时间序列X的标准差。
(2) 基于噪声序列最大样本熵的阈值估计应用
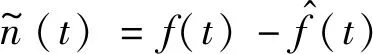
(11)
(12)
(3) 基于降噪序列最小样本熵的阈值估计应用
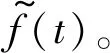
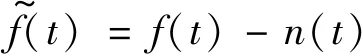
(13)
(14)
2.1.2 基于单样本熵阈值估计方法的局限性
(1) 样本熵值对噪声集合完整度表征的影响
样本熵值用于表征时间序列复杂度,却无法描述序列集合的完整度,复杂度最大的噪声序列并不一定是全部噪声信号的完整集合。相反,完整集合的噪声序列可能由于相似元素样本量的增加导致样本熵值下降。在降噪处理中,最大样本熵值下的噪声序列最复杂,可能不是全部噪声的完整集合情况,所以根据噪声序列最大样本熵值估计得到的阈值存在保守、偏小的风险,得到的降噪信号去噪不完全。同样的,基于降噪序列最小样本熵估计阈值,随着阈值增大降噪序列样本熵降低,估计得到的阈值存在偏大的风险,使信号降噪程度过度加强,重构信号信息缺失。

图2 基于样本熵极值的阈值估计模型Fig.2 Threshold estimation model based on sample entropy extreme value
以图1(b)所示的局放单次脉冲含噪信号为试验对象,噪声估计信号和降噪估计信号的样本熵曲线分别见图2(a)和图2(b)。按照最大熵原则选取阈值为0.101 0,在此阈值下对信号进行降噪,效果如图3(a)所示,结果表明,基于噪声序列最大样本熵下的阈值进行小波降噪,得到的重构信号中仍然含有噪声成分,降噪不完全;按照最小熵原则选取阈值为0.800 0,在此阈值下对信号进行降噪,效果如图3(b)所示,结果表明,过度降噪造成重构信号故障信息缺失。
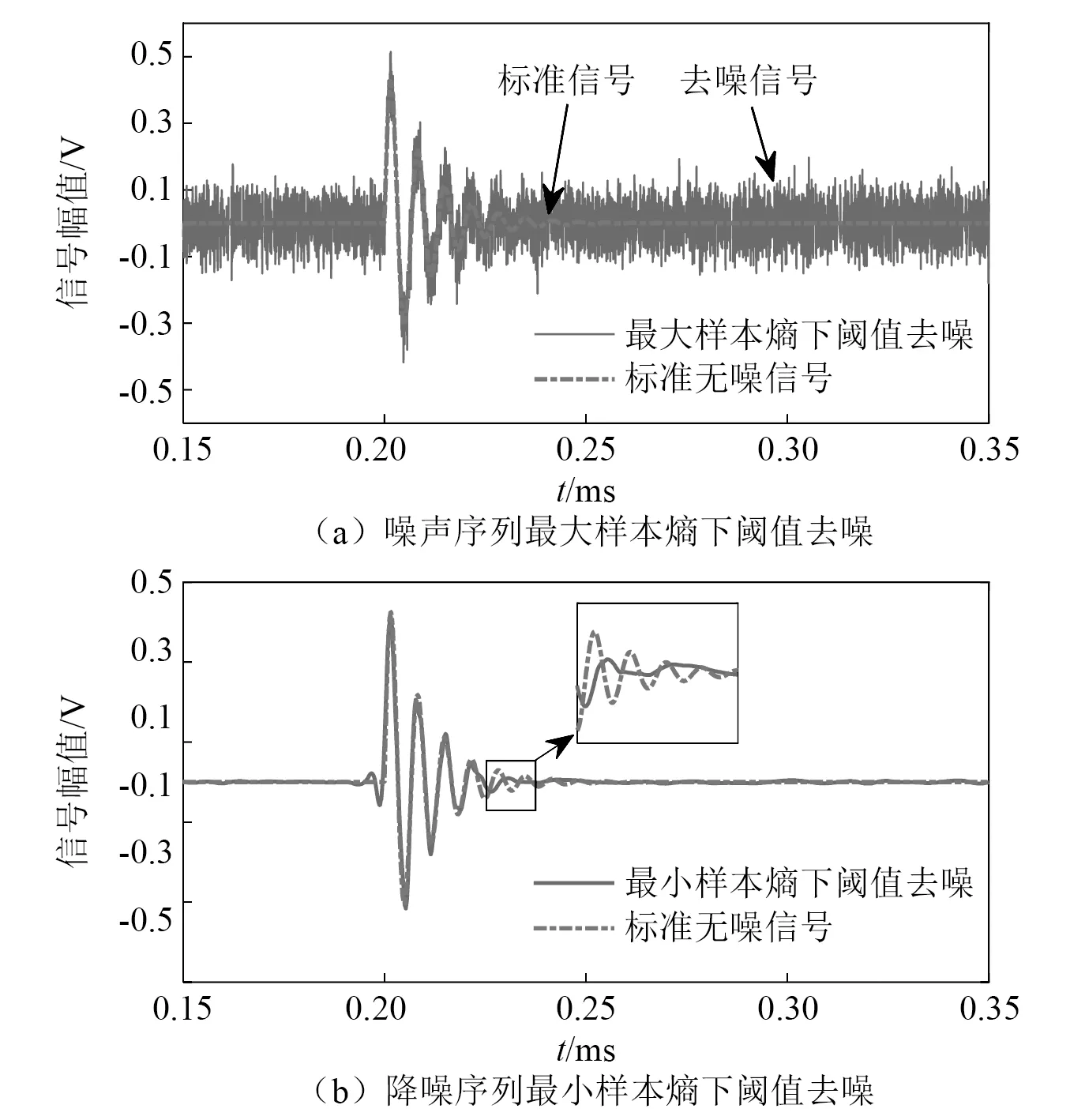
图3 基于样本熵极值下的阈值降噪效果Fig.3 Noise reduction effect based on the threshold under the extreme value of sample entropy
(2) 阈值步长对样本熵极值搜索速度和精度的影响
在传统样本熵阈值估计算法中,阈值的惯性步长为一固定值,当步长设置过大时,容易影响全局搜索精度,使阈值估计值陷入局部最优;当步长设置过小时,会影响全局搜索速率,造成巨大计算资源消耗。针对图1(b)所示的仿真信号,设置降噪阈值范围为[0.01,1.01],不同步长下的最大样本熵线性搜索结果如表1和图2(a)所示。当阈值以步长k=0.025线性递增时,获得的样本熵值曲线精度最高,但迭代次数最多,运算时间最长,最大样本熵值的搜索速率低、计算负担大;当阈值以步长k=0.100线性递增时,运算时间变短,资源消耗相对减小,但搜索精度下降,得到的最大样本熵值陷入了局部解。
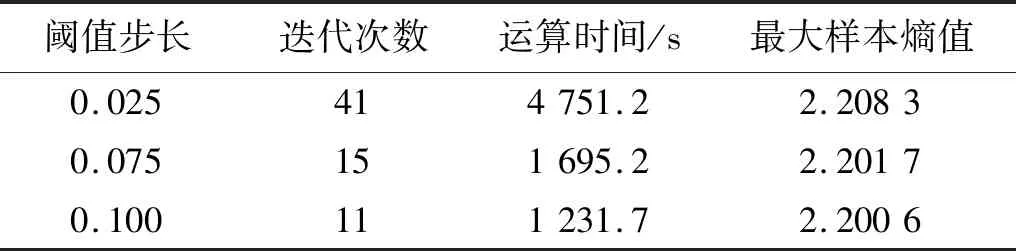
表1 不同步长下最大样本熵线性搜索结果Tab.1 Linear search result of maximum sample entropy value under asynchronous length
2.2 综合熵模型及其曲率拐点
针对上述2个局限性提出一种基于综合熵的最优阈值快速估计方法。按照2.1.1节,选取样本熵参数m=2,r=0.2std(X),计算降噪信号序列样本熵值Sf,噪声信号序列样本熵值Sn,定义如式(15)所示的综合熵(comprehensive entropy,CE)模型。
(15)
不同阈值作用下的降噪效果不一致,得到的综合熵值也不同。在阈值域内,噪声序列样本熵值Sn先增后减,降噪序列样本熵值Sf不断减小,经过最优阈值节点后,信号降噪效果变化不明显,样本熵Sn和Sf值变化缓慢,使综合熵Cλ值变化缓慢,研究认为最优阈值点位于综合熵曲线变化走势的拐点,称其为曲率拐点Kmax。不同于单序列样本熵最值估计问题,本文最优阈值的估计问题归结为综合熵曲率拐点的估计,如式(16)所示。
(16)
2.3 基于二分变步长非线性搜索的阈值快速估计
为了协调定步长线性迭代法存在的搜索精度与搜索速度的矛盾,本文引入非线性的惯性步长,采用二分变步长快速估计法,随着搜索进行,步长逐渐缩小。搜索流程Ⅰ如图4所示。首先,求解初始阈值对应的综合熵曲率集;接着,以最大曲率对应阈值为中心,以二分阈值差为步长寻找中心域前后的阈值并考察其熵线曲率情况,不断迭代逼近曲率拐点和最优阈值。值得说明的是,综合熵是以信号处理后得到的降噪序列和噪声序列为计算基础,所以算法中需要提前确定阈值函数,而对于确定性序列,最优阈值往往是固定的,与阈值函数种类选取无映射关联,为避免函数参量的影响,本文以硬阈值函数作为阈值寻优的试验性函数,具体步骤如下:
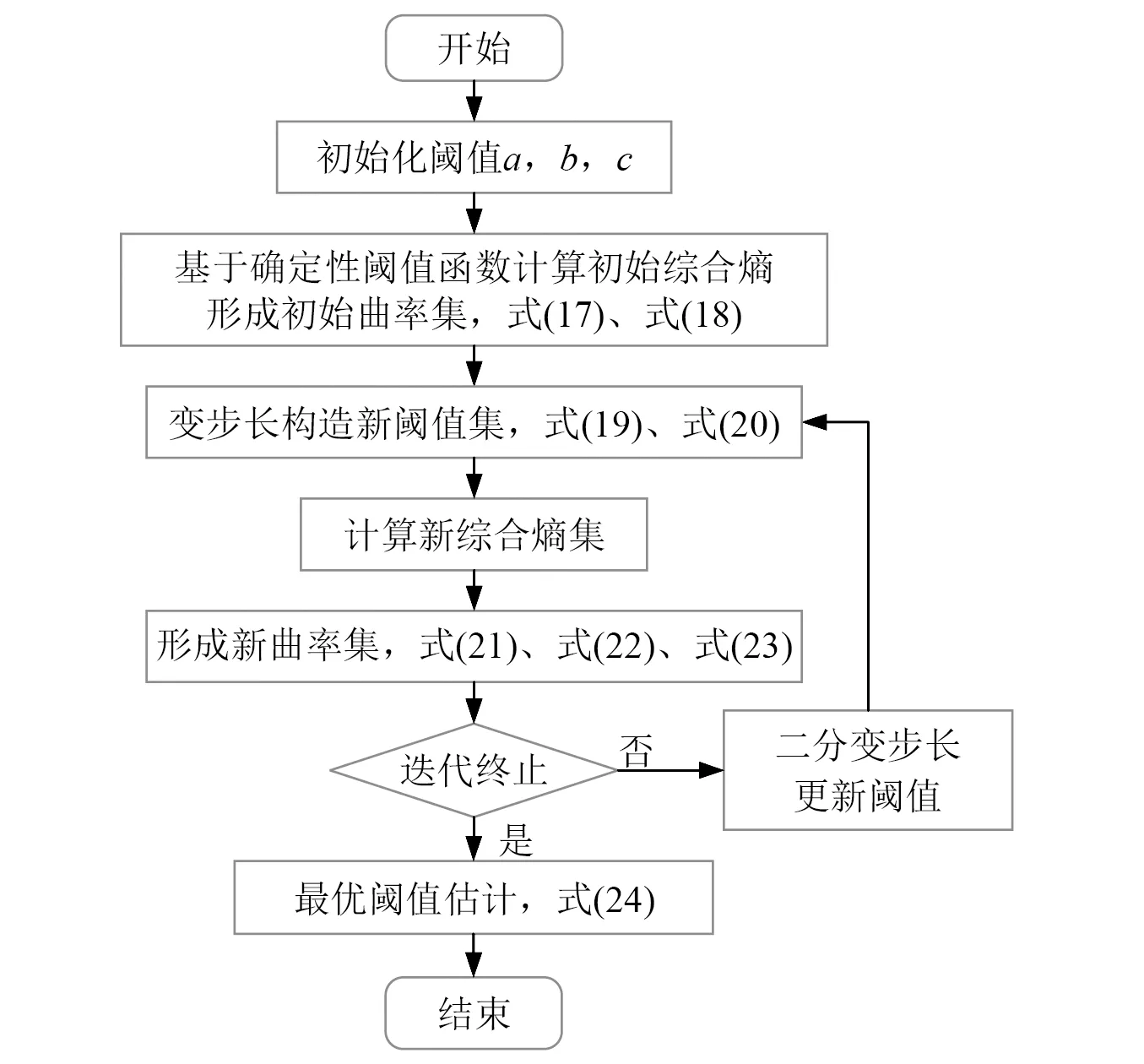
图4 基于快速综合熵的最优阈值估计(流程Ⅰ)Fig.4 Estimation of optimal threshold based on fast comprehensive entropy (Process Ⅰ)
步骤1设置阈值范围λ⊂[a,c],迭代次数n,为使最优阈值有效地包含于该范围中,λ的下限a应不大于“噪声最大样本熵法”得到的偏小估计值,上限c应不小于“降噪最小样本熵法”得到的偏大估计值;
步骤2计算初始离散阈值域下的估计信号样本熵,针对离散阈值集{a,b,c},b=(a+c)/2,基于试验性函数估计各阈值下的降噪信号和噪声信号,并计算其样本熵值Sfa,Sna,Sfb,Snb,Sfc,Snc;
步骤3计算初始离散阈值域下的综合熵曲率值,根据样本熵计算阈值对应综合熵Cza,Czb,Czc及其曲率Kb,Kc值,形成离散曲率集{Kb,Kc};
(17)
(18)
步骤4半步长构造新的离散阈值域,选择当代最大曲率Kmax⊂{Kb,Kc}下对应的阈值b1,以b1为中心,阈值域b1的前位a1为首元素,(b1-a1)/2为步长构造新阈值a2,b2,顺序形成下一代离散阈值集{a1,a2,b1,b2},若Kb=Kc,则取Kc下对应阈值b1为中心,(b1-a1)为步长构造新阈值;
(19)
(20)
步骤5考察新阈值集各元素对应曲率值,计算新一代各阈值下估计信号的样本熵值Sfa1,Sna1,Sfa2,Sna2,Sfb1,Snb1,Sfb2,Snb2。进而计算a2,b1,b2阈值下综合熵曲率值,形成新离散曲率域{Ka2,Kb1,Kb2};
(21)
(22)
(23)
步骤6终止迭代,判断是否满足迭代条件,若满足则最大曲率值为估计曲率拐点,对应的阈值即为最优估计阈值,如式(24)所示;否则转至步骤4基于半步长构造新一代离散阈值集,继续考察新阈值处的曲率,不断逼近最优阈值点。
(24)
3 改进阈值函数实现
3.1 经典阈值函数及改进
3.1.1 传统阈值函数及其局限性
经典的小波阈值函数包括硬阈值函数和软阈值函数,分别如式(25)和式(26)所示[21-25]。
(25)
(26)
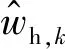
硬阈值函数表达如式(25)所示,将尺度系数绝对值与阈值比较,小于或等于阈值的系数置为0,大于阈值的系数保留不变,同阈值下的硬阈值函数降噪充分、效果明显,但在正、负阈值处存在间断的阶跃点,使处理后的高频尺度系数不连续,信号重构会产生振荡。为此提出了如式(26)所示的软阈值函数,尺度系数绝对值与阈值比较,小于或等于阈值的系数置为0,大于阈值的系数置为该点与阈值的差值,软阈值函数实现系数在阈值处的连续性,抑制了重构信号振荡,然而却对系数的处理整体进行了收缩,重构信号较标准信号会存在恒定偏差。
3.1.2 改进阈值函数
(1) 改进阈值函数基本原理
针对上述软、硬阈值函数存在的局限性,本文提出一种含参量的改进阈值函数,如式(27)所示。
(27)
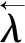
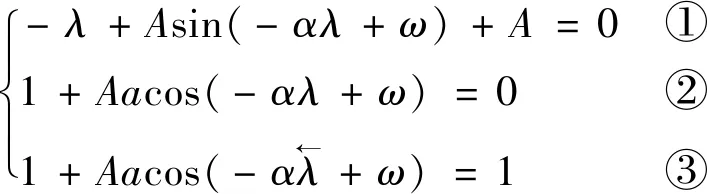
(28)
根据式(28)求得函数相关参数
(29)
(30)
(31)
一般取k1=k2=0,假设某阈值为5,根据式(27)~式(31),所提改进函数模型如图5所示。

图5 改进阈值函数模型Fig.5 Improved threshold function model
(2) 改进阈值函数特点
1) 连续性讨论——在函数左半支对阈值点和前向阈值点处函数连续性讨论如下:

2) 可导性讨论——在函数左半支对阈值点和前向阈值点处函数可导性讨论如下:
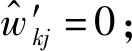
改进函数为关于原点对称的奇函数,右半支函数同样具有连续可导性。综上,所提改进阈值函数在全阈值域内具有连续可导性。
3.2 基于平滑过渡数的函数参数选择方法
改进阈值函数具有一个可调节的品质因子α参量(见图5)。α值不会对函数的连续性与可导性产生影响,但决定了其他参量的取值,不同α下得到的改进函数不同,一定程度上约束了降噪效果和重构信号的品质,根据式(29),α可由式(32)估计得到
(32)
由式(32)可知,函数阈值幅度A越小,品质因子α值越大,函数越接近硬阈值函数特性,A越大,α值越小,函数越接近软阈值函数特性,在阈值点不发生漂移的情况下,通过调整α值实现改进函数向软、硬阈值函数平滑过渡和继承。为快速完成对参量α的选择,本文建立平滑过渡数模型,定义硬过渡数Ph和软过渡数Ps表达式用以刻画函数软、硬化程度。
(33)
(34)
Ph+Ps=1
(35)
硬过渡数Ph和软过渡数Ps取值范围为0~100%,当阈值幅度A=λ/2时,过渡数Ph=1,Ps=0,表明函数100%继承硬阈值函数特性,代入式(32)中可得α趋于无穷大;当阈值幅度A=λ时,过渡数Ph=0,Ps=1,表明函数100%继承软阈值函数特性,此时α=1/λ。
基于平滑过渡数的参数选择示例:设置硬过渡数Ph=99.6%,软过渡数Ps=0.4%,根据式(33)~式(35)有A=1.004λ/2;代入式(32)中得α≈1/0.063λ,阈值λ由最优阈值估计法获取;基于α值,根据式(30)和式(31)计算其余参量,最终得到改进阈值函数,流程Ⅱ如图6所示。
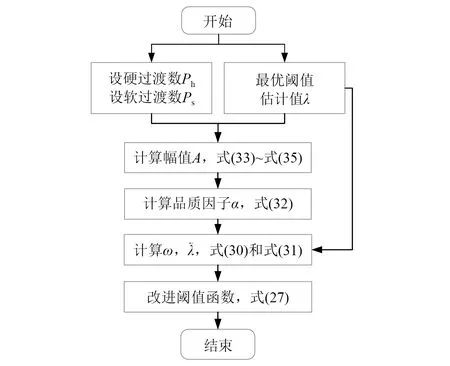
图6 改进阈值函数参数计算(流程Ⅱ)Fig.6 Improve the parameter calculation of the threshold function(Process Ⅱ)
4 基于改进阈值估计和改进阈值函数降噪方法
4.1 改进降噪方法过程概述
基于快速综合熵改进最优阈值估计和改进小波阈值函数实现对信号st的降噪过程,如图7所示,具体步骤如下:

图7 基于改进阈值估计和阈值函数的信号降噪过程Fig.7 Signal denoising process based on improved threshold estimation and improved threshold function
步骤1根据信号特性选取合适的小波基,确定信号分解层数,对含噪信号st进行小波尺度分解,得到低频系数与高频系数;
步骤2根据第2章,基于二分变步长非线性搜索法快速估计序列综合熵曲率拐点,得到估计最优阈值λ;根据第3章,基于平滑过渡指数模型完成函数参数选择,得到改进阈值函数;
步骤3基于最优阈值估计值λ和改进阈值函数,对高频系数进行处理,得到降噪后的高频系数;
步骤4基于分解的低频系数与阈值处理后的降噪高频系数进行小波重构,得到降噪后的信号。
4.2 降噪效果性能评估指标
为了验证本文改进小波阈值方法的有效性,选择信噪比(signal-noise ratio,SNR)、均方根误差(root mean square error,RMSE)和皮尔逊相关系数(Pearson correlation coefficient,PCC)作为降噪效果评价指标,降噪后信号与标准信号的SNR越大,RMSE越小,PCC越大,表明降噪信号与标准信号相关度越好,降噪效果越好。
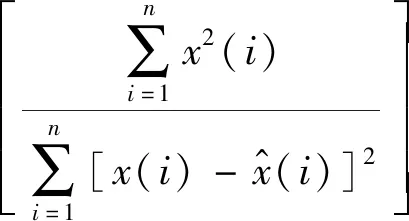
(36)
(37)
(38)
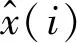
5 基于改进阈值估计和改进阈值函数降噪实例
5.1 实例一:基于MATLAB实验室的局部放电超声波仿真信号降噪应用
5.1.1 平台环境与小波分解预处理
基于MATLAB实验室环境搭建如图1(b)和图1(c)的含噪局放超声波脉冲仿真信号,按照文献[26]的方法基于互相关系数实现信号分解的小波基和分解层数优化选择,分别计算不同db小波基(db2~db10)、不同分解层数(4层~11层)下降噪信号与标准信号的互相关系数值,以互相关系数最大值为目标优化选择小波分解参数,试验结果如图8所示。图8(a)表明,不同小波基函数下降噪效果不一致,得到的互相关系数值也不同;图8(b)表明,随着分解层数的增加,信号分辨率愈高,降噪效果愈好,互相关系数值增大,当超过最优分解层后,降噪效果提升不明显甚至呈下降趋势。根据试验结果,针对单次局部放电超声波仿真信号,小波参数选取为互相关系数值最优的db6小波、9层分解;针对周期局部放电超声波仿真信号,则选取db5小波、7层分解。
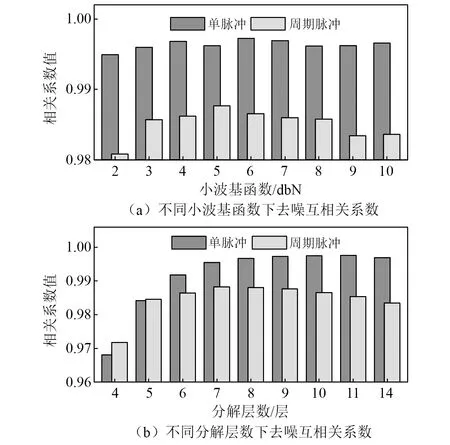
图8 基于互相关系数的小波基和分解层数选取试验Fig.8 Experiment on the selection of wavelet basis and decomposition level based on PCC
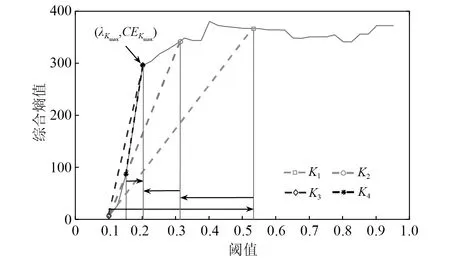
5.1.2 最优阈值估计试验
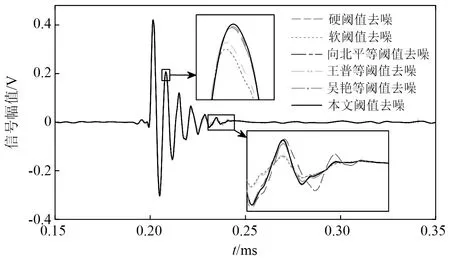
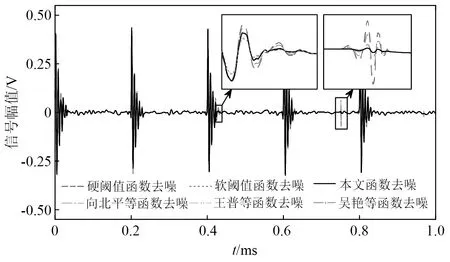
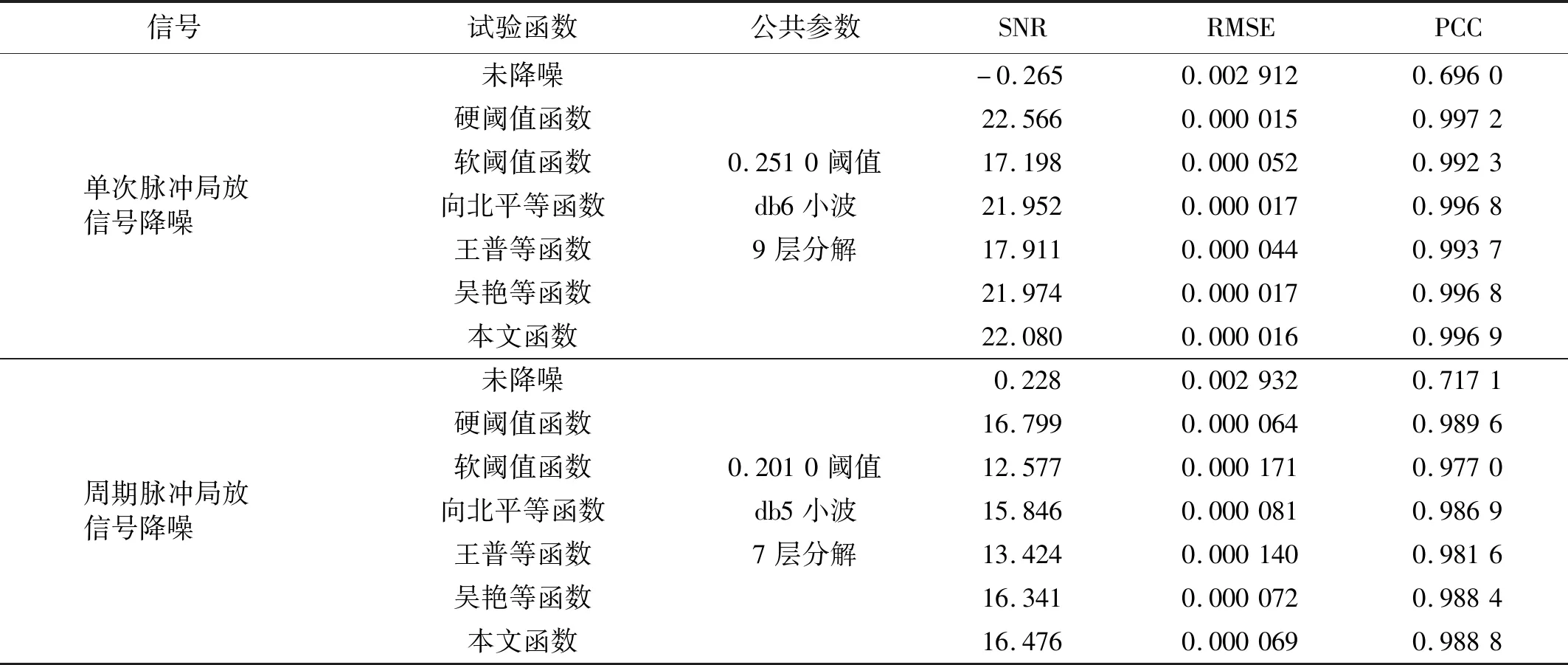
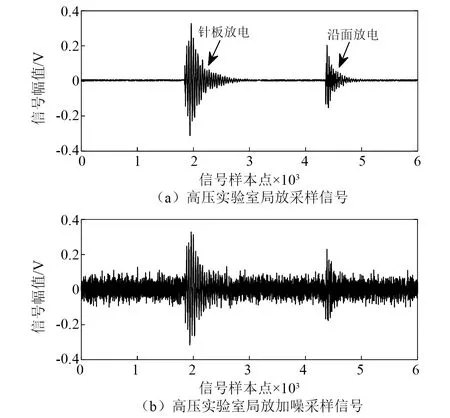
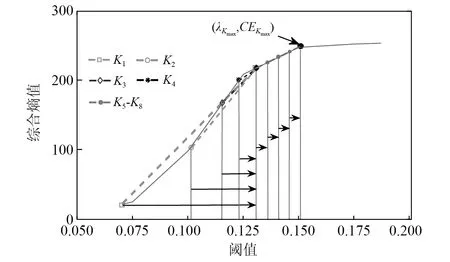
针对局放超声波脉冲仿真信号,表2列出了各种方法下的阈值估计值。由表2可知:单脉冲工况下噪声最大样本熵法估计的偏小阈值为0.101 0,降噪最小样本熵法估计的偏大阈值为0.800 0,根据阈值范围选取原则(见2.3节),可设λ⊂[0.101 0,0.800 0],其综合熵曲线如图9所示;周期脉冲工况下阈值估计偏小值为0.101 0,偏大值为0.951 0,可设λ⊂[0.101 0,0.951 0],其综合熵曲线如图10所示。对曲率拐点的搜索,若采用小步长惯性迭代,搜索次数和计算负荷增大;若采用大步长惯性迭代则会导致搜索精度下降。本文所提的二分变步长非线性搜索法的寻优过程如图9和图10中矢量箭头所示,5次搜索的熵曲率值大小为K1 为验证所提快速阈值估计方法的有效性,分别与噪声序列最大样本熵阈值估计法、降噪序列最小样本熵阈值估计法、经典统一阈值估计法[27]进行对比,不同估计方法下估计阈值的降噪效果见表2。由表2可知:不论是单脉冲还是周期脉冲的局放超声波信号,基于噪声序列最大样本熵估计的阈值相对最小,由于小阈值作用信号使噪声处理不完全,降噪后信号的SNR值相对最小,RMSE值相对最大,PCC值相对最小,降噪效果最不理想;而基于降噪序列最小样本熵估计的阈值由于偏大而产生过度降噪,得到的降噪信号与标准信号仍然存在偏差;经典的统一阈值估计法简单快速,但估计得到的阈值存在偏大风险,对于复杂的周期脉冲信号降噪效果不明显;本文所提二分变步长非线性搜索法寻优收敛速度快、精度高,估计阈值作用下降噪信号的SNR值最大,RMSE值最小,PCC值最大,获得了良好的信号降噪效果。 图9 基于综合熵的最优阈值估计(针对单次局放信号)Fig.9 Optimal threshold estimation based on comprehensive entropy(For a partial discharge signal) 图10 基于综合熵的最优阈值估计(针对周期局放信号)Fig.10 Optimal threshold estimation based on comprehensive entropy(For periodic partial discharge signal) 表2 不同阈值估计方法下的超声波仿真信号降噪Tab.2 Noise reduction of ultrasonic simulation signal under different threshold estimation methods 5.1.3 改进阈值函数降噪试验 为验证所提改进阈值函数降噪方法有效性,针对局放超声波脉冲仿真信号,分别采用硬阈值函数、软阈值函数、向北平等、王普等、吴艳等所提改进阈值函数和本文改进阈值函数降噪方法进行对比,各阈值函数模型如图11所示。按照参数选择方法,设置硬过渡数Ph=99.96%,软过渡数Ps=0.04%,得到A=1.004λ/2,α≈1/0.063λ,根据表2,两种仿真信号的最优估计阈值λ分别取0.251 0,0.201 0,其中各阈值函数降噪得到的重构信号如图12、图13所示,降噪效果如表3所示。 图11 各阈值函数模型对比Fig.11 Comparison of various threshold function models 图12 基于改进阈值函数的信号降噪(针对单次局放信号)Fig.12 Signal noise reduction based on improved threshold function (For a partial discharge signal) 图13 基于改进阈值函数的信号降噪(针对周期局放信号)Fig.13 Signal noise reduction based on improved threshold function (For periodic partial discharge signals) 表3 不同阈值函数方法下的超声波仿真信号降噪Tab.3 Noise reduction of ultrasonic simulation signal under different threshold function methods 由图11可知,几种改进阈值函数均介于软、硬阈值函数之间,试验结果表3表明,相对于未去噪情况,所有降噪方法均有效提升了SNR值和PCC值,降低RMSE值,参数约束域内的降噪效果为:软阈值<王普等<向北平等<吴艳等<本文<硬阈值函数降噪方法。 由表3可知:硬阈值函数降噪的SNR值和PCC值最大、RMSE值最小,降噪效果显著,然而图13所示结果表明此方法在0.75 ms左右处重构信号时出现了振荡缺陷;软阈值函数在阈值域内连续,有效抑制了重构振荡,但图12所示结果表明此方法在信号脉冲波峰处与标准信号存在恒定偏差,SNR值和PCC值较小、RMSE值较大,降噪效果有待提升;王普等所提函数特性最接近软阈值函数,较其他改进方法其降噪效果提升不明显;向北平等和吴艳等所提函数连续且接近硬阈值函数,降噪效果提升有效,但在阈值邻域内存在函数不可导、系数过渡不平滑的局限性;而本文改进阈值函数在参数约束域内较其他改进方法SNR值和PCC值较大,RMSE值较小,降噪效果最好,对单脉冲、周期脉冲局放超声波信号均具有良好的降噪适应性。 5.2.1 平台环境与小波分解预处理 高压电力设备在不同结构、不同区域处发生局部放电使绝缘缺陷类型多样化,其中沿面放电、针板放电是两种经典的局放类型[28]。基于高电压实验室搭建模拟这两类局部放电的试验场景,接线如图14所示,220 V 交流电源接入电源控制箱,控制变压器产生最高100 kV的高电压,有效满足高压放电的要求,放电模型一端加载高压,另一端通过地线接入大地,试验用超声波传感器置于金属支撑板完成信号捕捉,示波器用以传感器信号接入与观察。 图14 基于高电压实验室的局部放电模拟试验Fig.14 Partial discharge simulation experiment based on high voltage laboratory 本文高压局放试验中控制产生35 kV等级的高电压,并分别加载在针板放电和沿面放电模型上,传感器捕捉放电产生的超声波信号,整理后获得6 000个两类局放信号采样序列点,如图15(a)所示,人工加噪后的局放超声波信号如图15(b)所示。对于该类型试验信号,按照单脉冲局放仿真信号分解方法,选取db6作为小波基函数,信号分解层数设置为9层较为合适。 5.2.2 最优阈值估计试验 针对含噪局放试验超声波脉冲信号,表4列出了各种方法的阈值估计值。由表4可知,噪声最大样本熵法估计的偏小阈值为0.074 0,降噪最小样本熵法估计的偏大阈值为0.181 0,根据阈值范围选取原则(见2.3节),可设λ⊂[0.074 0,0.181 0]。基于本文非线性搜索法估计最优阈值,寻优过程如图16中矢量箭头所示,经过8次快速搜索后的综合熵曲率值如图16所示,得到最优估计阈值为0.151 0。 图15 局部放电超声波试验信号Fig.15 Partial discharge ultrasonic experimental signal 图16 基于综合熵的最优阈值估计(针对局放试验信号)Fig.16 Optimal threshold estimation based on comprehensive entropy (For partial discharge experimental signal) 以图15(a)所示信号为标准信号,采用多个阈值估计方法进行对比试验,结果见表4。由表4可知:基于噪声序列最大样本熵估计的阈值较为保守,降噪后信号的SNR值和PCC值相对最小,RMSE值相对最大,降噪效果相对最差;基于降噪序列最小样本熵估计法和经典统一阈值估计法得到的阈值存在偏大风险,降噪效果并非最优;而基于本文所提二分变步长非线性搜索法估计阈值相对最优,降噪后信号的SNR值和PCC值最大,RMSE值最小,降噪效果相对最优。 5.2.3 改进阈值函数降噪试验 为验证所提改进阈值函数对局放超声波信号降噪的工程应用性,仍然采用如图11所示的硬阈值函数、软阈值函数、向北平等、王普等、吴艳等所提阈值函数和本文阈值函数降噪方法进行对比,根据表4最优阈值λ取0.151 0。其中各阈值函数降噪方法的重构信号如图17所示,各阈值函数下降噪效果如表5所示。 表4 不同阈值估计方法下的超声波试验信号降噪Tab.4 Denoising of ultrasonic experimental signals under different threshold estimation methods 图17 局部放电超声波试验信号降噪Fig.17 Partial discharge ultrasonic experiment signal noise reduction 表5 不同阈值函数方法下的超声波试验信号降噪Tab.5 Denoising of ultrasonic experimental signals under different threshold function methods 由表5可知,在硬阈值函数降噪方法下由于降噪充分,重构信号的SNR值和PCC值最大,RMSE值最小,降噪效果相对最优。图17表明,该函数作用降噪重构信号保留了较为完整的脉冲波峰信息,但在5 300左右采样点处存在重构振荡现象,会对下一阶段的局放故障识别与处理造成信息干扰。而软阈值函数去噪能有效地抑制振荡现象,但由于对尺度系数的收缩处理,重构信号的脉冲幅值被消减,脉冲波峰信息完整性缺失,降噪效果不理想,同样会对故障识别与处理造成信息干扰。表5表明,向北平等、王普等和吴艳等改进方法的降噪效果并非最优,而本文改进阈值函数在抑制重构振荡的同时最接近硬阈值函数降噪品质,保留了较为清晰完整的故障信息,相较其他改进函数,本文所提改进函数具有良好的降噪充分性。 文中提出一种基于改进最优阈值估计和改进阈值函数的小波阈值降噪优化方法,并实现高压电力设备局部放电超声波信号降噪应用,通过仿真及试验验证,得出如下结论: (1) 在融合噪声序列和降噪序列样本熵信息基础上,建立综合熵模型,以综合熵曲率拐点对应的阈值为最优阈值,克服了单序列样本熵极值估计阈值存在局部解的情况。同时提出二分变步长非线性阈值搜索法,有效地协调了传统定步长阈值搜索存在搜索速度和精度的矛盾。试验结果表明,所提搜索方法较传统方法具有显著的搜索速度和精度优势。 (2) 提出了介于软、硬阈值函数之间的改进阈值函数,该函数具有全阈值的连续可导性,通过定义的平滑过渡数模型Ph和Ps实现函数参数快速选择,优化所提函数从软特性到硬特性的继承和过渡。 (3) 基于MATLAB实验室与高电压实验室分别将改进方法应用于单次局放与周期局放信号,针板局放与沿面局放信号降噪场景。结果表明,所提降噪方法有效地继承了软、硬阈值函数优势,在抑制重构振荡的同时具有降噪充分性,重构信号保留了较为完整的故障信息。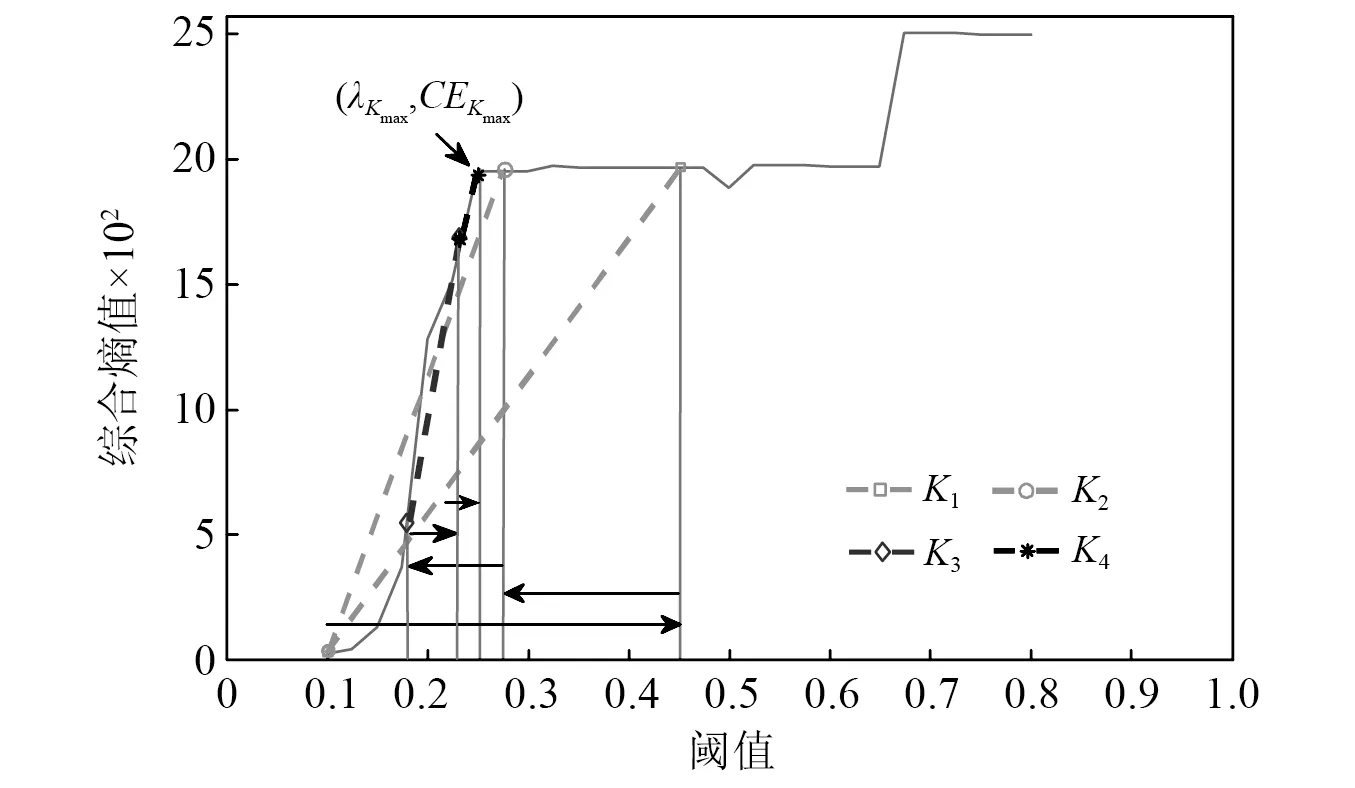


5.2 实例二:基于高电压实验室的局部放电超声波试验信号降噪应用




6 结 论
