基于ANSYS Workbench的锚链轮轻量化设计

王 杰，王 震，陈 超，骆书虎，邵振华

（1.江苏科技大学机械工程学院，江苏 镇江 212003；2.江苏政田重工股份有限公司，江苏 南通 226000）

0 引 言

当前船舶工业正朝着“绿色船舶”的方向发展，锚绞机作为船舶锚泊系统的重要配套设备，其在技术上也正朝着经济、节能、绿色环保的方向发展［1］。锚链轮作为锚绞机在起锚、抛锚、系泊和带缆时与锚链直接接触的部件，其结构设计的可靠性对保障锚机和船舶的安全运行有重要影响［2］。传统的锚链轮主要根据GB／T 3179—1996标准设计，往往依靠经验公式，采用较高的安全系数保证结构的安全性，缺少比较精确的强度计算，这使得锚链轮的体积庞大，结构笨重，机械传动效率不高，材料和能源浪费较多［3］。因此，对锚链轮轻量化技术进行研究，优化锚链轮结构，提高其传动效率，是锚绞机和其他甲板机械未来发展的必然趋势。

近年来，国内外已有很多学者对船用锚绞机各部件的轻量化设计进行研究，例如：李曦［4］对液压锚绞机墙架进行了有限元分析，确定了墙架的优化设计空间，运用Optistruct软件对墙架板厚进行了优化设计；李文钊［5］对锚绞机卷筒和制动机构进行了有限元计算，确认了结构的变形失效部位与实船故障部位的一致性，利用NX NASTRAN软件对失效部位进行了优化设计；WU等［6］对锚机底座进行了静力学分析和模态分析，得到了底座模型可优化的空间，利用ANSYS软件对底座结构进行了拓扑优化设计；王志明［7］对船用锚机的链轮轴进行了刚柔耦合仿真分析，得到了链轮轴在实际工况下的动应力历程，为链轮轴的优化设计提供了理论依据。本文以船用锚机的锚链轮为研究对象，利用ANSYS Workbench软件对其进行瞬态动力学分析和预应力模态分析，并基于多目标遗传算法（Multi-Objective Genetic Algorithm，MOGA）对锚链轮的尺寸进行优化，探寻对锚链轮进行轻量化设计的可行性和最终能达到的轻量化程度。

1 锚链轮有限元分析

本文以正多边形啮合的五齿锚链轮为研究对象，采用SolidWorks软件对其进行三维建模。为建立准确的三维实体模型，在创建锚链轮模型时要充分考虑其可能遇到的工况和安装要求。同时，为提高后期有限元网格划分的质量，提升有限元分析的精度和计算速度，根据圣维南原理［8］，对模型进行适当的简化，去掉对有限元计算影响不大的螺栓孔和倒角。锚链轮简化模型见图1。

图1 锚链轮简化模型

1.1 瞬态动力学分析

首先，为保证模型在导入软件过程中的完整性，避免元素丢失，将锚链轮三维实体模型以x_t格式导入ANSYS Workbench中；其次，定义锚链轮的材料属性，本文参照日本标准SC450（相当于国标ZG 230-450）选取锚链轮材料，其屈服强度为230 MPa，弹性模量为2.11×105MPa，泊松比为0.311，密度为7.83 g／cm3；最后，对锚链轮进行有限元网格划分，综合考虑计算量和计算精度，设置单元格大小为40 mm，采用自由网格划分的方式，划分的网格单元数为79 374个，节点数为137 654个。创建的锚链轮有限元网格模型见图2。

图2 锚链轮有限元网格模型

在锚机进行起锚操作过程中，锚链轮与锚链只有1～2个齿相啮合，这里为简化分析，只考虑1个齿与锚链相啮合的情况，锚链轮的受力区域为图3中的区域A。由于锚链轮的受力面为曲面，很难确定其受力方向，这里以曲面上所受压力代替锚链与锚链轮啮合时产生的啮合力。已知锚链轮过载时所受拉力F为858 kN，曲面面积A为0.029 4 m2，则曲面所受拉力P为

图3 锚链轮载荷添加

瞬态动力学分析以锚链轮过载时刻为中心，分析过载瞬间前后共计0.1 s时间内锚链轮所受应力的变化情况。首先，设置锚链轮瞬态分析初始时间载荷步为0.002 s，最短时间载荷步和最长时间载荷步分别为0.002 s和0.010 s，计算周期为0.100 s；其次，在锚链轮上添加一个转动副，并给定一个转速，使锚链轮的转速在前半个周期内迅速增加到1 rad／s，在后半个周期内保持不变；最后，将大小为29.18 MPa的压力载荷添加到啮合曲面上，方向为垂直于曲面（见图3），并确保载荷在0.050 s内迅速增大到最大值，在结束时刻减小到0。设置完成之后，开始进行分析计算，得到锚链轮在1个周期内的应力变化曲线，见图4。

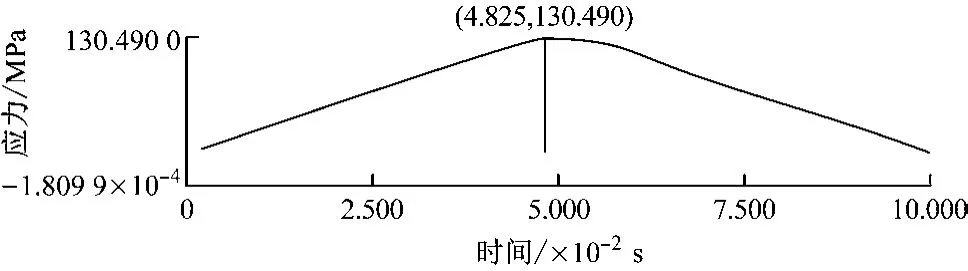
图4 0～0.100 s内锚链轮应力变化曲线

由图4可知，随着锚链轮所受压力的不断增大，其最大等效应力值也不断增大，并在0.048 25 s时达到最大，此时锚链轮等效应力云图和总变形位移云图分别见图5和图6。由图5和图6可知，锚链轮最大应力出现在链轮轴与锚链轮内壁连接处，最大等效应力值为130.49 MPa，远小于锚链轮材料的屈服强度，此时其侧壁的最大位移变形量为15.127 mm，满足轻量化设计需求。

图5 0.048 25 s时锚链轮等效应力云图

图6 0.048 25 s时锚链轮总变形位移云图

1.2 预应力模态分析

锚链轮在起锚过程中一直处于转动状态，不仅要满足强度要求，而且要满足振型和固有频率要求，避免与其他部件产生共振，因此要对其进行模态分析。

首先，将锚链轮实体模型以x_t格式导入ANSYS Workbench软件中；其次，在Workbench模态分析系统中定义锚链轮的材料属性、单元格大小和网格划分方式；接着，在锚链与锚链轮啮合处添加一个垂直于受力面的压力，同时在链轮内孔面添加圆柱约束，以约束锚链轮的径向运动和轴向运动，只让其有圆周方向的转动；最后，取模态阶数为6进行模态分析计算。锚链轮模型固有频率值和振型云图分别见表1和图7。

图7 锚链轮前6阶模态振型云图

表1 锚链轮固有频率值

从表1和图7中可看出：锚链轮的前3阶模态的固有频率值在173.65～183.61 Hz，是锚链轮的主要振动模态；锚链轮的后3阶模态的固有频率值都在186.30 Hz以上，是锚链轮的局部振动模态。锚链轮工作时，链轮轴转动和齿轮传动产生的激振频率都在100 Hz以下，远低于锚链轮的最低固有频率，因此锚链轮不会与其他部件产生共振，其动态特性满足设计要求。

2 锚链轮尺寸优化设计

由锚链轮的瞬态动力学分析和预应力模态分析结果可知，锚链轮的原结构模型仍具有一定的优化设计空间，而锚机工作时锚链与锚链轮的啮合面为曲面，且锚链轮齿形设计相对标准化，因此对锚链轮的齿形进行优化较为困难。这里在上述有限元分析的基础上，只针对锚链轮的轮毂和侧壁等应力较小的部位进行尺寸优化。

1）锚链轮的实体模型是由截面旋转拉伸得到的，优化锚链轮结构就是对截面尺寸进行调整。锚链轮旋转拉伸截面图见图8。

图8 锚链轮旋转拉伸截面图

这里以锚链轮轮毂的厚度d1、两侧壁的厚度d2和d3为设计变量，以锚链轮的最大应力为约束条件，以最小化质量和一阶固有频率为优化目标，要求锚链轮的质量M在允许的范围内尽可能地小，其1阶固有频率fn1在允许的范围内尽可能地高，构建2个目标函数，即：F1（X）＝min M（X）；F2（X）＝max fn1。

锚链轮尺寸优化数学模型为

式（2）中：d1为轮毂的厚度；d2为左侧壁的厚度；d3为右侧壁的厚度；F1（X）为最小化质量；F2（X）为最大应力。

2）根据建立的锚链轮尺寸优化模型，运用ANSYS Workbench软件的Design Explorer优化设计模块对锚链轮进行基于MOGA的尺寸优化，整个优化过程见图9。

图9 锚链轮结构参数优化流程

3）优化算例分析。

本算例利用ANSYS Workbench软件提供的MOGA进行计算分析。该算法是非支配排序遗传算法Ⅱ的变种算法，多用于对全局最小值和最大值进行求解［9-10］。优化算法具体参数设置：种群总数为100个；交叉概率和变异率分别为0.8和0.1；最大迭代次数为40次；最大候选点个数为3个。同时，使锚链轮质量函数最小化和一阶频率函数最大化，并约束最大应力，使其小于许用应力值。优化迭代过程以Pareto解集前沿分布80%的样本收敛，最终经过40次迭代之后得到1组Pareto最优解集，并生成3组最合理的优化设计结果。得到锚链轮初始结构和3种优化方案对比见表2。

表2 锚链轮初始结构和3种优化方案对比

4）优化结果。

从表2中可看出，3组优化方案的设计变量都在一定的区间内趋于稳定，为得到最优的优化结果，分别针对3组数据重新建模，并对得到的锚链轮模型进行瞬态分析，结果见图10。由图10可知，在0.1 s时间内，优化方案三的锚链轮的弹性变形量最小，最大弹性变形量为4.973 4×10－4mm，因此确定优化方案三为锚链轮的最佳优化方案。

图10 锚链轮3组优化方案弹性变形量对比

3 优化锚链轮验证分析

考虑后续机械加工的需求，对优化方案三的各尺寸作圆整化处理，即d1＝10 mm，d2＝36 mm，d3＝31 mm，得到最终的优化结构。添加与优化前相同的边界条件和载荷状况，分析验证优化后锚链轮的动态特性，结果见图11和图12。由图11和图12可知：优化后锚链轮的最大应力值由原来的130.49 MPa增加到了134.72 MPa，仍在材料的许用应力范围内；优化后锚链轮的最大位移变形量由原来的15.127 mm增加到了16.603 mm，对锚链轮刚度的影响较小。表3为优化后基座模型固有频率值。由表3可知，优化后锚链轮各阶固有频率均有所提高，其中1阶固有频率由原来的173.65 Hz增加到了184.45 Hz，较好地实现了1阶固有频率最大化的目标。

图11 优化后锚链轮等效应力云图

图12 优化后锚链轮最大位移变形云图

表3 锚链轮优化后基座模型固有频率值

表4为锚链轮优化前后各性能参数对比。由表4可知：优化后锚链轮的总质量减少了118.73 kg，减重率为3.25%；优化后锚链轮的最大等效应力和总位移变形量略有增大，对锚机整体结构的可靠性不会产生影响；优化后锚链轮的固有频率有所提高，远大于链轮轴自身转动和大小齿轮间传动产生的激振频率，对整体结构的稳定性不会产生影响。由此可知，基于MOGA对锚链轮进行轻量化设计能达到预期的效果，使锚链轮在满足整体结构强度和刚度要求的同时，达到减轻重量的目的，满足轻量化设计要求。

表4 锚链轮优化前后各性能参数对比

4 结 语

本文以正多边形啮合的五齿锚链轮为研究对象，通过对其轻量化设计的流程和方法进行研究，提出基于ANSYS Workbench软件对锚链轮的结构进行优化设计。根据锚链轮的瞬态动力学分析和预应力模态分析结果，确定锚链轮的可优化区域，为其轻量化设计提供科学的理论依据；基于锚链轮力学分析结果，确定利用轮毂的厚度d1、两侧壁厚度d2和d3等3个参数构建以锚链轮质量最小化和1阶固有频率最大化为目标的尺寸优化数学模型；利用MOGA对锚链轮的尺寸进行优化，确定这3个参数的最优解集，并通过瞬态分析确定锚链轮尺寸的最终结构。通过对优化前后锚链轮的结构进行对比分析得出：优化后锚链轮的总质量减小了3.25%，较好地实现了减重的目的；同时，锚链轮的强度、动态特性和抗振性能得到了提高，满足锚链轮设计的经济性和安全性要求，为其他船舶的机械辅助设备的轻量化设计提供了理论依据。