全驱动自主水下机器人回收路径跟踪模糊滑模控制

潘 伟，曾庆军，姚金艺，朱志宇，夏 楠，马洪潮

（江苏科技大学电子信息学院，江苏 镇江 212100）

0 引 言

近年来，海洋资源的大力开发和利用为各种海洋工程装备的设计和制造创造了有利条件［1］。自主式水下机器人（Autonomous Underwater Vehicle，AUV）是海洋开发领域的重要工具之一，具有机动性好和巡航范围大等优点，随着信息技术的不断发展，其在军事和科学研究领域的作用越来越重要。然而，受自身能源的限制，AUV的作业时间有限，这就需及时回收机器人，对其进行能源补给和维修［2］。路径跟踪对AUV精准执行使命、顺利完成回收等任务具有重要影响。

深水海域的油气资源比较丰富，为更好地开发油气资源，世界各国都在大力发展深水作业技术［3］，从一开始的试验型机器人，到能投入生产和应用的产业化机器人，研制出了多种具有不同结构和功能的水下机器人。国外比较著名的水下机器人研究机构［4］有美国MIT Sea Grant AUV实验室和日本东京大学水下机器人应用实验室（Underwater Robotics Application Laboratory）等；国内比较先进的水下机器人研究机构［5］有中国科学院沈阳自动化研究所、哈尔滨工程大学和中国海洋大学等。目前，已有很多学者围绕上述问题，针对AUV的三维路径跟踪开展研究。例如：王晓伟等［6］采用反步法设计了水平面跟踪控制器，利用微分器对未知状态和不确定项进行了估计；刘昌鑫等［7］采用非线性模型预测控制方法设计了AUV的约束路径跟踪控制律，以解决有约束路径跟踪控制问题。路径跟踪控制主要是将其解耦为水平面（横向）控制和垂直面（垂向）控制，本文以自主研发的“探海Ⅱ型”全驱动AUV为研究对象，对水平面控制方法进行研究，采用模糊滑模路径跟踪控制器增强AUV在回收过程中的抗干扰性能。

1 “探海Ⅱ型”全驱动AUV数学模型

1.1 回收控制系统概述

“探海Ⅱ型”全驱动AUV样机具有跟踪精度高和控制灵活等特点，其对接系统由对接坞系统和AUV系统2部分组成。AUV本体控制系统主要由导航模块、控制模块、推进模块、双目视觉处理单元和电源模块组成，其中导航模块主要包括全球定位系统（Global Positioning System，GPS）、光纤惯导、多普勒计程仪和深度计，在对接时，额外介入超短基线和双目视觉定位数据进行数据融合导航。该型AUV含有5台推进器，属于全驱动型AUV。

对接坞控制系统主要负责采集对接坞传感器的数据，并将其发送给干端监控台，同时可通过通信定位一体机向水下机器人发送信息和指令。对接坞控制系统主要由密封壳体、水密插座、电源模块、采集计算机、网络交换机和搭载的传感器组成，其中搭载的传感器包括GPS、深度传感器、姿态传感器、漏水传感器、标志灯、水下摄像头、通信定位一体机（安装在对接器上）和限位传感器（安装在对接器上）等。在对接阶段，AUV与对接坞通过超短基线的无线通信功能进行信息交互。图1为“探海Ⅱ型”全驱动AUV回收对接系统。

图1 “探海Ⅱ型”全驱动AUV回收对接系统

1.2 坐标系

水下机器人建模包含运动学建模和动力学建模2部分，通过运动学解释物体在运动过程中的位置、速度和加速度的几何关系，通过动力学分析机器人在加速运动过程中的动力变化。在讨论AUV运动模型时，通常要建立2个参考系，即大地坐标系（E－ξηζ）和运动坐标系（O－xyz）。图2为AUV运动坐标系和大地坐标系示意图，其中：大地坐标系的原点E在水平面上，ξ轴指向地理北向，η轴指向地理东向，ζ轴指向地心；运动坐标系的原点在AUV上，x轴、y轴和z轴分别指向AUV的艏部、右舷和底部。

图2 AUV运动坐标系和大地坐标系示意图

1.3 垂直面模型

本文所述数学模型主要来源于Timothy Prestero提出的REMUS型水下机器人的仿真模型，AUV的运动学方程以浮心作为运动坐标系原点，刚体六自由度空间运动方程为

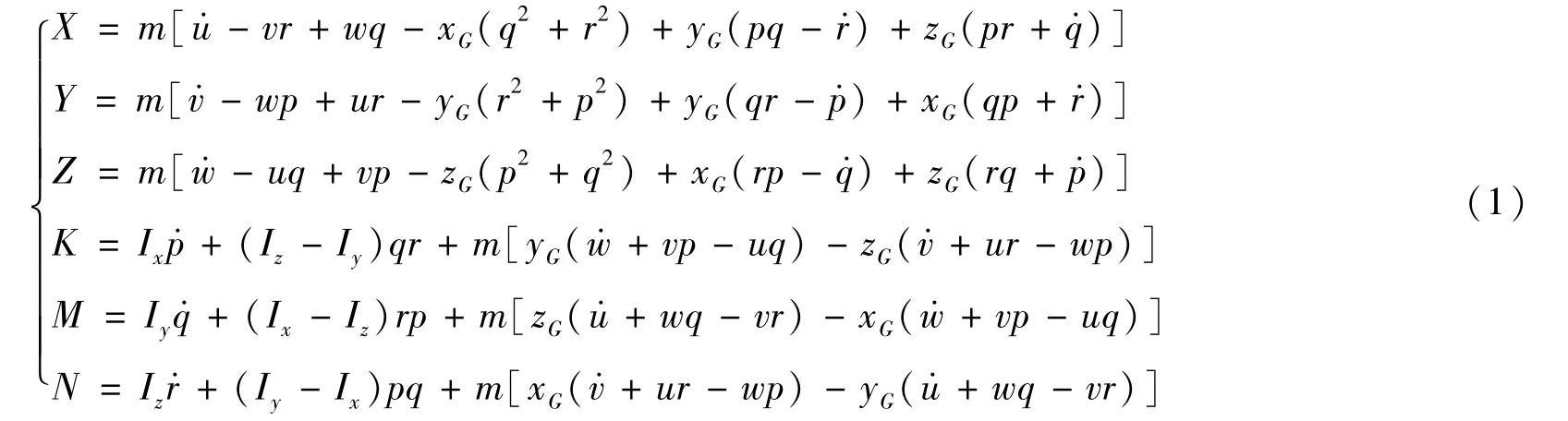
式（1）中：m为AUV本体的质量；xG、yG和zG分别为AUV的重心在3个坐标轴上的坐标；Ix、Iy和Iz分别为AUV在3个坐标轴上的转动惯量；u、v和w分别为AUV的速度在3个坐标轴上的分量；p、q和r分别为AUV的角速度在3个坐标轴上的分量。

基于AUV六自由度模型，可得到简化的AUV垂直面运动方程。

1）z轴方向的浮潜运动学方程为

2）y轴方向的纵倾运动学方程为

式（2）和式（3）中：Fi为高斯白噪声；Zw｜w｜、Zq｜q｜、Zuq、Zuw、Mw｜w｜、Mq｜q｜、Muq、Muw、Mw·、Mq·、Zw·和Zq·为水动力参数；Zg为z轴方向的受力；Mg为重力；Zprop和Mprop分别为z轴方向的推力和y轴方向的推力矩；xg和zg为重心坐标。

1.4 水平面模型

在w＝0，p＝0，q＝0的条件下，首先简化得到水平面AUV的运动学方程。

1）x轴方向的进退运动学方程为

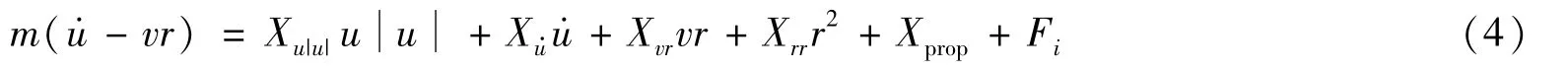
2）y轴方向的平移运动学方程为

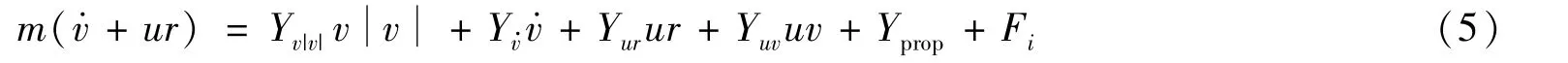
3）z轴方向的转艏运动学方程为

式（4）～式（6）中：Xu｜u｜、Xu·、Xvr、Xrr、Yv｜v｜、Yv·、Yvr、Yuv、Nv｜v｜、Nr｜r｜、Nr·、Nur和Nuv为水动力参数；Xprop、Yprop和Nprop为各自方向上的力和力矩。

1.5 环境干扰

通常情况下，干扰为风、浪、流，AUV在水下作业时的主要干扰来自流。水流只影响水动力作用的辐射力，若水流速度为U（ux，uy，uz），机器人速度为UAUV（u，v，w），水流对机器人的影响也可看作机器人相对水流反方向的运动，相对运动速度vr可表示为

一般不考虑垂向水流，可类似回复力对水平方向的水流进行求解。

2 基于模糊滑模的路径跟踪控制器设计

2.1 水平面控制器设计

AUV水平面控制有两大问题：一是非线性模型的不确定性；二是洋流波浪的随机性。滑模控制不仅能很好地解决AUV控制系统的不确定性问题，而且对外界干扰响应不灵敏，具有很强的鲁棒性，但其带来的抖振问题难以解决。

若给定AUV水平面期望值为

式（8）中，ψ为航向角。则跟踪误差e为

得到跟踪误差的一阶导数为

选取滑模面函数

选取滑模控制指数趋近律为

根据水平面控制模型，取

可得

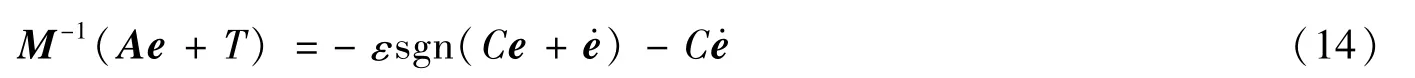
整理得到控制律

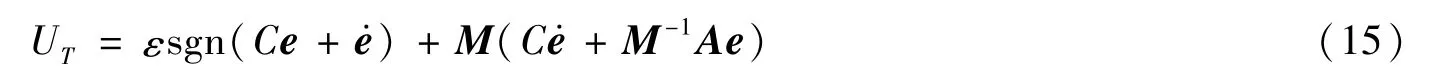
将滑模控制器中趋近律的符号函数用模糊控制的输出代替，以解决滑模控制带来的抖振问题，即

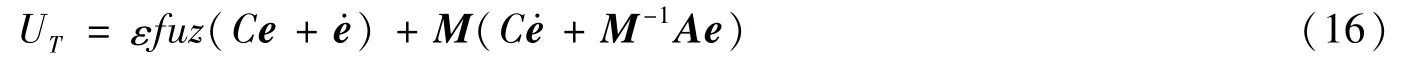
将滑模控制器中趋近律的符号函数用模糊控制的输出代替，该模糊控制为单输入单输出，输入为e，输出为fuz（s），因此定义的输入输出论域为

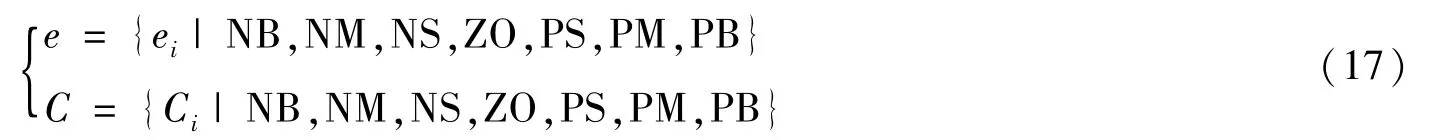
模糊语言变量为NB（负大）、NM（负中）、NS（负小）、ZO（零）、PS（正小）、PM（正中）和PB（正大）。选取的输入和输出的范围为［－3，3］。隶属度函数选取三角形隶属函数，解模糊策略选取重心法。

模糊规则如下：

1）If A＝NB，then B＝NB；

林徽因也恳求保住永定门，她声嘶力竭地痛斥：“你们现在拆了真古董，等有一天你们后悔了，只能盖个假古董了。”然而她的恳求无效，真古董最终还是被无情地拆除了。

2）If A＝NM，then B＝NM；

3）If A＝NS，then B＝NS；

4）If A＝ZO，then B＝ZO；

5）If A＝PS，then B＝PS；

6）If A＝PM，then B＝PM；

2.2 垂直面控制器设计

AUV垂直面控制采用S面控制方法。S面控制器的控制模型为

式（18）中：k1和k2为控制系数，可将其类比为PID（Proportional Integral Derivative）控制器中的PD系数；Δu为调整项，可将其看作一段时间内的固定干扰力或其他调整因素；e和为控制输入信息，e在AUV中看作深度和艏向角误差信息在AUV中看作深度和艏向角误差变化率；u为控制输出，在AUV中看作对应推进器的推力和转矩。

3 AUV三维路径跟踪控制仿真及湖试

3.1 三维路径跟踪控制仿真分析

分别设计模糊滑模控制器和PID控制器，并采用MATLAB对AUV进行水下六边形路径跟踪仿真。仿真采用的参数是“探海Ⅱ型”全驱动AUV水动力等模型参数。主推进器给定恒定推力，目标深度为3 m，定常洋流速度为0.1 m／s。AUV三维路径跟踪仿真结果见图3。AUV切换目标航线时会产生一定的超调，出现超调会使AUV的跟踪路线产生误差，从而导致这2种控制器的跟踪时间不一致；模糊滑模控制器在海流干扰下的三维路径跟踪性能优于PID控制器。表1为AUV六边形跟踪平均误差，给出了模糊滑模控制器和PID控制器跟踪六边形时每条边跟踪的平均误差。

图3 AUV三维路径跟踪仿真结果

表1 AUV六边形跟踪平均误差

3.2 湖试及结果分析

湖试在苏州某湖进行，试验环境良好，水质清澈且湖底平坦，水深范围为5～20 m，湖水流速约为2 kn。设计AUV的航速为0.8 kn，下潜深度为1 m，设置的GPS初始经纬度坐标为（120.560 356 1°E，31.892 150 88°N），返航目标经纬度坐标为（120.560 150 1°E，31.892 097 47°N），任务总时长为9 min。图4为湖试试验图；表2为AUV三维路径跟踪试验部分数据。

表2 AUV三维路径跟踪试验部分数据

图4 湖试试验图

图5为AUV三维路径跟踪曲线。从图5中可看出，AUV可按设定的轨迹由起始点A出发，下潜至点B开始自主导航，依次经过点C、点D和点E之后上浮并行进到回收坞所在的点F处完成对接。AUV转弯时，其主推进器始终处于运行状态，存在一定的惯性，因此在进行直角跟踪导航时需要一定的反应时间，从而回到预设的轨迹上。表3为深度、航向角和纵倾角误差分析结果。从表3中可看出，AUV的跟踪效果较好，纵倾角和航向角误差均值小于8°，深度误差均值小于0.1 m。

图5 AUV三维路径跟踪曲线

表3 深度、航向角和纵倾角误差分析结果

4 结 语

路径跟踪作为AUV的重要功能，一直是国内外学者研究的热点。本文介绍了“探海Ⅱ型”全驱动AUV的回收控制系统，针对其垂直面、水平面和环境干扰建立了数学模型。水平面艏向角控制采用滑模控制器；考虑到海流干扰和滑模控制带来的抖振问题，引入模糊控制取代滑模控制中趋近律的符号函数；垂直面采用S面控制。仿真分析和湖试结果表明，该AUV运行稳定，设计的控制器有效，能较好地完成三维路径跟踪任务，满足全驱动AUV的水下实际任务需求。