典范对应分析数据模拟物种丰度计算方法
2022-11-17刘志丽吴亚玲周铁军
刘志丽, 吴亚玲, 周铁军
(湖南农业大学信息与智能科学技术学院,长沙 410128)
1 引 言
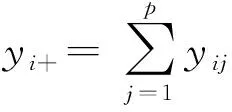
(1)
典范对应分析需要检验每个物种j在不同样地上的丰度标准值qij与这些样地上环境因子是否存在显著的线性关系.对检验方法的有效性分析需要由某种分布随机生成的环境因子的数据依据线性关系或无关系生成标准矩阵Q.现在的问题是,如何由矩阵Q确定绝对频率矩阵Y=[yij]n×p?正是因为这个问题的存在,使得参考文献[1]附录D在进行检验方法的有效性分析时没有提供检验发生第二类错误的仿真计算结果.因此解决由标准矩阵Q计算物种丰度矩阵Y问题具有理论意义.当然从式(1)可以知道,对于两组成比例的丰度数据,其标准矩阵Q是相同的,即由Q并不能唯一确定物种丰度矩阵Y,但我们希望能够确定其中一组丰度值.
2 等效的齐次线性方程组存在半正解问题
由式(1)得
(2)
对j求和得
于是有
(3)
类似地,由(2)对j求和还可得
(4)
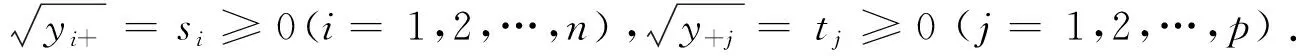
所以
(5)
从等式(3)-(5),问题化为要求满足下列条件的非负不全为0的si(i=1,2,…,n)和tj(j=1,2,…,p):
(6)
(7)
(8)
用矩阵表示为
QTs=0, Qt=0, sTs=tTt.
显然s=0, t=0能够满足上述方程(6)-(8),但没有实际意义.因此希望求方程组(6)-(8)的非负不全为0的解.确定了si与tj后,就可以根据下式计算yij,
(9)
注意到条件(8)可以通过将齐次方程(6)与(7)的非零解单位化后得到.所以问题的关键是如何求齐次方程(6)与(7)的非负非零解使yij≥0.齐次线性方程组的非负非零解一般称为半正解,如果解的全部分量均为正,则称为正解.
参考文献[2]获得了齐次线性方程组Ax=0有正解的充分必要条件,即这个方程组存在若干个减列方程组, 它们都是有正解的极小方程组,并且这些极小方程组全部列向量的并集的秩等于A的秩.但确定极小方程组及其正解不是一件简单的事.参考文献[3]对一类正线性方程组讨论了它的半正解的存在性,而参考文献[4]也从系数矩阵A出发给出了齐次线性方程组Ax=0有非负解的充分条件及必要条件.
通过以下方法求齐次方程(6)与(7)的半正解.显然容易求得齐次线性方程组(6)或(7)的基础解系,所以问题转化为如何用齐次线性方程组的一组基础解系表示出它的一个半正解.参考文献[5]对基础解系中自由未知量取标准单位向量且只有两个向量的条件下讨论了半正解的存在性.本文研究用齐次线性方程组的任一组基础解系(含两个或三个向量)表示出它的一个半正解的条件,并给出数值计算方法.
3 由基础解系表示半正解的条件
显然,如果基础解系只含一个非零向量,除非它的分量全部为正或全部为负,否则它不能表示出一个半正解.
3.1 基础解系至少含分量不全为正的两个向量
先考虑基础解系至少含分量不全为正的两个向量情形,即它们的分量中即有正分量也有负分量.这些正负分量在两个向量中的位置有三种情形,一是负分量个数少的向量其负分量所在位置和负分量个数多的相应位置上的分量都是负分量;二是负分量个数少的向量其负分量所在位置和负分量个数多的相应位置上的分量都是正分量;三是负分量个数少的向量其负分量所在位置和负分量个数多的相应位置上的分量有一部分是负分量,有一部分是正分量.设基础解系中向量α1中有k个负分量,向量α2中有l个负分量,不妨假设k≥l.
情形1 设基础解系中含有向量
α1=(-a11,…,-a1l,-a1,l+1,…,-a1k,a1,k+1,…,a1n),
α2=(-a21,…,-a2l,a2,l+1,…,a2k,a2,k+1,…,a2n),
其中aij≥0.记A={1,2,…,l},B={l+1,l+2,…,k},C={k+1,k+2,…,n}.如果k=l,则B=∅.
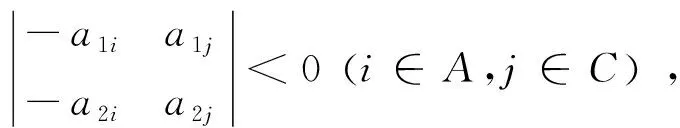
证向量α1与α2的线性组合可以表示为
c1α1+c2α2=(…,-c1a1i-c2a2i,…,-c1a1i1+c2a2i1,…,c1a1j+c2a2j,…).
如果a1j=0,必有c1<0,c2>0,使得
-c1a1i-c2a2i>0, -c1a1i1+c2a2i1>0,c1a1j+c2a2j>0.
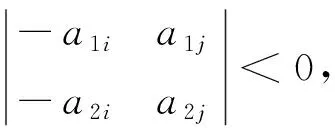

于是得到
-c1a1i-c2a2i>0, -c1a1i1+c2a2i1>0,c1a1j+c2a2j>0.
故得到
c1α1+c2α2>0.
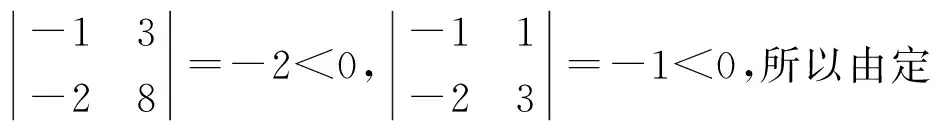
情形2 设基础解系中含有向量
α1=(-a11,…,-a1k,a1,k+1,…,a1,k+l,a1,k+l+1,…,a1n),
α2=(a21,…,a2k,-a2,k+1,…,-a2,k+l,a2,k+l+1,…,a2n),
其中aij≥0,n≥k+l.记A={1,2,…,k},B={k+1,k+2,…,k+l},C={k+l+1,k+l+2,…,n}.如果n=k+l,则C=∅.由于
-α2=(-a21,…,-a2k,a2,k+1,…,a2,k+l,-a2,k+l+1,…,-a2n),
于是-α2中负分量个数n-l大于等于α1中负分量个数k,即n-l≥k,且α1中负分量所在位置为A,-α2中负分量位置为A∪C⊃A,故就是情形1.因此得到定理2.

情形3 设α2中l个负分量只有s个位置与α1中负分量位置相同,其余负分量位于α1的正分量位置.不妨设基础解系中向量
α1=(-a11,…,-a1s,-a1,s+1,…,-a1k,a1,k+1,…,a1,k+l-s,a1,k+l-s+1,…,a1n),
α2=(-a21,…,-a2s,a2,s+1,…,a2k,-a2,k+1,…,-a2,k+l-s,a2,k+l-s+1,…,a2n),
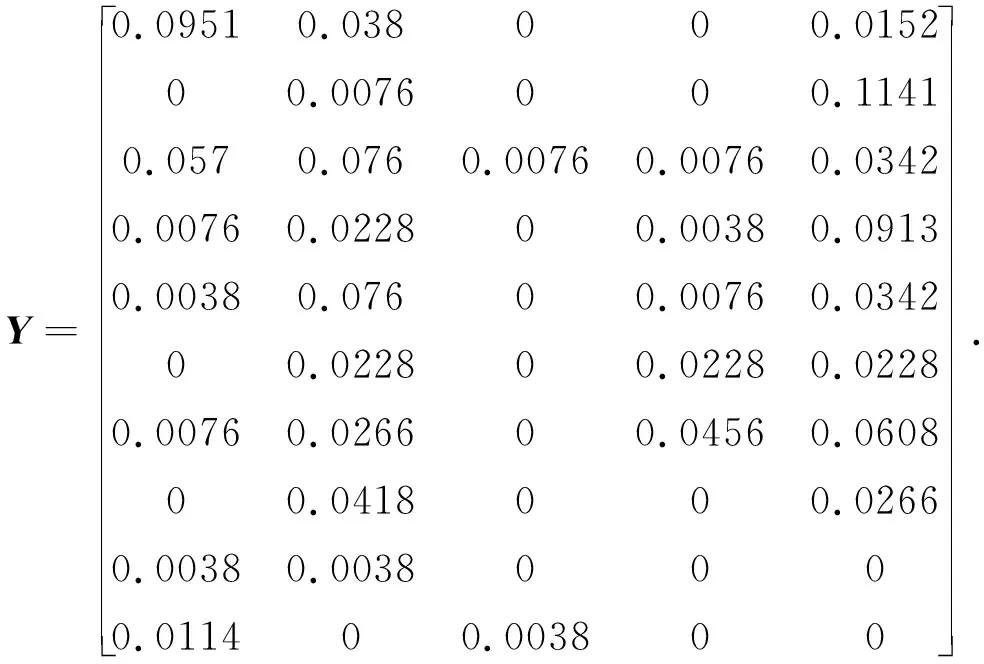
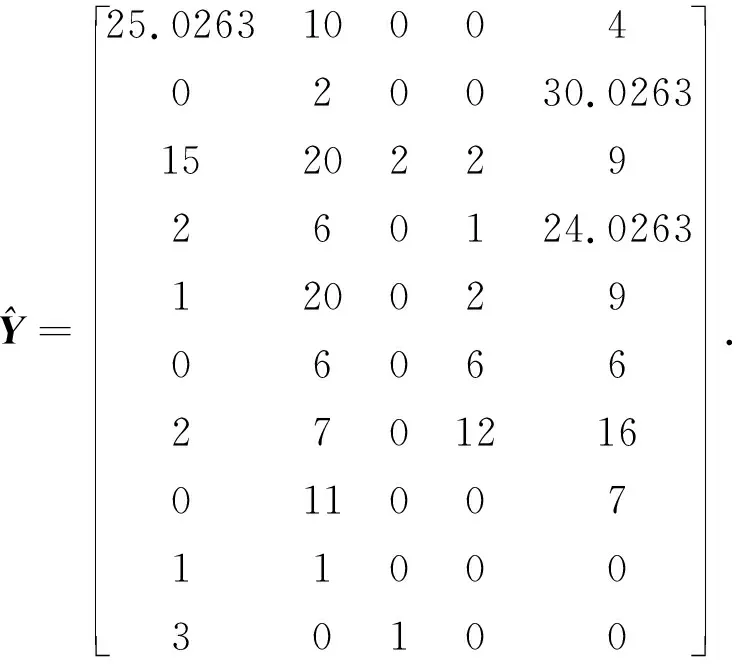
其中aij≥0,s α1=(-a11,…,-a1s,-a1,s+1,…,-a1k,a1,k+1,…,a1n), -α2=(a21,…,a2s,-a2,s+1,…,-a2k,a2,k+1,…,a2n). 下面考虑n>k+l-s,即D≠∅.假设存在常数c1与c2,使得 c1α1+c2α2=(…,-c1a1i-c2a2i,…,-c1a1i1+c2a2i1,…,c1a1j-c2a2j,…,c1a1j1+c2a2j1,…)>0. 其中i∈A,i1∈B,j∈C,j1∈D.因此有 c1a1i<-c2a2i,c1a1i1 如果c2>0,则由c1a1i<-c2a2i知c1<0,而由c1a1j>c2a2j知c1>0.如果c2<0,则由c1a1i1 只需考虑三个向量中任意两个的负分量位置不全部相同的情形.不妨设基础解系中有向量 α1=(-a11,…,-a1s,-a1,s+1,…,-a1k,a1,k+1,…,a1,k+l-s,a1,k+l-s+1,…,a1n), α2=(-a21,…,-a2s,a2,s+1,…,a2k,-a2,k+1,…,-a2,k+l-s,a2,k+l-s+1,…,a2n), 其中aij≥0,s 其中a3j≥0. 如果A-,A+,B-,B+,C-,C+,D-,D+都不是空集,则由c1α1+c2α2+c3α3>0可得 -c1a1i1-c2a2i1-c3a3i1>0,i1∈A-, (10) -c1a1i2-c2a2i2+c3a3i2>0,i2∈A+, (11) -c1a1i3+c2a2i3-c3a3i3>0,i3∈B-, (12) -c1a1i4+c2a2i4+c3a3i4>0,i4∈B+, (13) c1a1j1-c2a2j1-c3a3j1>0,j1∈C-, (14) c1a1j2-c2a2j2+c3a3j2>0,j2∈C+, (15) c1a1j3+c2a2j3-c3a3j3>0,j3∈D-, (16) c1a1j4+c2a2j4+c3a3j4>0,j4∈D+. (17) 如果c2>0,c3>0,则由(10)推出c1<0,而由(14)推出c1>0,相互矛盾. 如果c2<0,c3>0,则由(12)推出c1<0,而由(16)推出c1>0,相互矛盾. 如果c2>0,c3<0,则由(11)推出c1<0,而由(15)推出c1>0,相互矛盾. 如果c2<0,c3<0,则由(13)推出c1<0,而由(17)推出c1>0,相互矛盾. 因此,如果A-,A+,B-,B+,C-,C+,D-,D+都不是空集,即α3的正、负分量分别位于A,B,C,D中,则不能由α1,α2,α3线性组合生成一个非负非零的解向量.所以A-,A+,B-,B+,C-,C+,D-和D+至少有一个空集,可以只考虑A-,B-,C-,D-四个集合中至少有一个是空集的情形,因为如果A+,B+,C+,D+中至少有一个空集,则-α3的负分量位置A-,B-,C-,D-四个集合中至少有一个是空集.A-,B-,C-,D-四个集合中至少有一个是空集共有10种情形. a1i1x+a2i1y>a3i1,i1∈A-, (18) a1i2x+a2i2y>-a3i2,i2∈A+, (19) a1i3x-a2i3y>a3i3,i3∈B-, (20) a1i4x-a2i4y>-a3i4,i4∈B+, (21) a1j1x-a2j1y<-a3j1,j1∈C-, (22) a1j2x-a2j2y (23) a1j4x+a2j4y (24) 其中(19)是显然成立的.如果其它6个不等式有解,则可以由α1,α2,α3线性组合生成一个非负非零的解向量.记 于是 所以不等式(18),(23)成立.又 所以(20),(21),(22)和(24)成立.因此正实数x,y就是方程组(18),(20)-(24)的一组解.从而由基础解系必可以线性表示出一个半正解. 成立,其中i1∈A-,i3∈B-,i4∈B+,j1∈A-,j2∈B+,j4∈B+,则由基础解系必可以线性表示出一个半正解. 证由不等式(c)可以知道a1j2a2j1-a1j1a2j2>0.根据条件(d),必存在正实数x使得 所以得 且 从而有 与 所以(22)与(23)成立.又 所以 从而 所以(20),(21)成立.因此正实数x,y就是方程组(18),(20)-(24)的一组解.从而由基础解系必可以线性表示出一个半正解. 可以将用齐次线性方程组的一组基础解系表示出它的一个半正解归结为一个二次规划问题.具体计算步骤如下: 第一步,求齐次线性方程组(6)的基础解系ξ1,ξ2,…,ξn-k; 第二步,由基础解系ξ1,ξ2,…,ξn-k确定齐次方程(6)的一个半正解 s=c1ξ1+c2ξ2+… +cn-kξn-k, 其中系数ci是如下二次规划问题的最优解: 其中b是一个任意设定的正向量,lc是一个负向量,规定c=(c1,c2,…,cn-k)T的取值下限,uc是正向量,规定c的取值上限.fi是任意正数.这是一个二次规划问题,可以通过Matlab 函数quadprog计算得到c. s=null(Q′); r=size(s,2); H=eye(r); f=rand(r,1); lc=-5*ones(r,1); uc=-lc; b=0.01*rand(n,1); c=quadprog(H,f,-s,-b,[],[],lc,uc); s=s*c; 第三步,将半正解s单位化得si. 类似地可以通过上述步骤计算齐次线性方程组(7)的半正解t,单位化后得ti. 例2取矩阵 利用上述算法可以计算得方程(6)的一个半正解 与(7)的半正解 它们都是单位向量. 进一步根据计算得到的两个半正解s与t,由(9)式计算得物种丰度矩阵如下: (25) 利用(1)式,可以由上述矩阵Y计算得到矩阵Q,这验证了提出的由Q逆算Y的方法的准确性.例2中的Q是由参考文献[1]中的第1~4及第6种蜘蛛在前10个样地上数量经(1)转化成的标准矩阵.如果我们将矩阵Y乘以10000/38,则可以得到 不难发现,除了3个带小数的数外,其它数据和原始观察数据一致,而且这三个带小数部分的数据其整数部分也是与相应观察值一致的. 研究典范对应分析置换检验的有效性时需要随机生成大量数据,利用齐次线性方程组半正解存在性有效地解决了由生成数据转换为物种丰度的计算问题.在齐次线性方程组基础解系至少具有两个分量不全为负的解向量情形下,给出了由这两个解向量线性表示半正解的充分条件,在不能由含两个分量不全为负的解向量线性表示半正解时,又给出了一组含三个分量不全为负的解向量的基础解系线性表示半正解的充分条件. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.3.2 基础解系至少含分量不全为正的三个向量
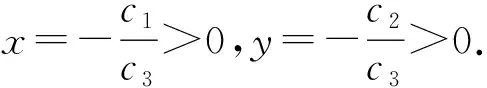
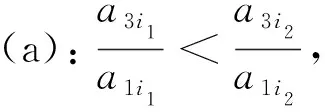


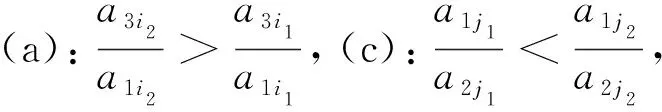
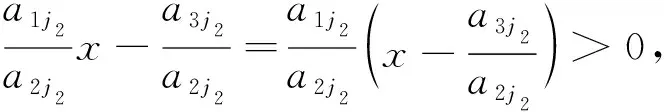
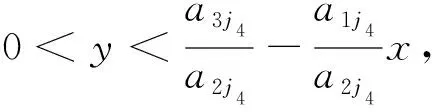
4 基础解系表示半正解的数值计算方法

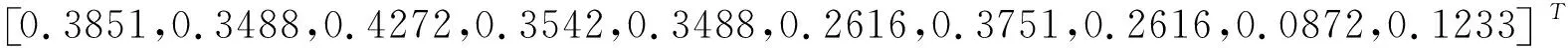
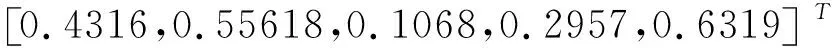
5 结 论
