非自治离散系统中的有界复杂性及等度连续性

张瑞丰， 朱姜慧

(合肥工业大学数学学院，合肥 230601)

1 引 言

动力系统的复杂性一直是动力系统研究中广受人们关注的领域，熵是刻画系统复杂性的重要不变量.一般认为熵为正的系统是比较复杂的，例如在作用下，已证明正熵系统是Li-Yorke混沌的[1].但对于某些简单的系统(如零熵系统等)，可以考虑系统复杂性函数本身，即系统中轨道的指数增长率.

最先提出这一想法的是参考文献[2]，他们研究了子转移的复杂性函数，并证明了此函数的有界性等价于系统的最终周期性.1980年，参考文献[3] 引入一个复杂性函数，这一函数是由与不变测度μ和误差ε相关的张成集的定义所扩展得到的.参考文献[4]研究了通过开覆盖定义的复杂性函数，并证明了复杂函数有界等价于该动力系统是等度连续的.随后参考文献[5]将Katok定义的复杂性函数进一步推广，对极大度量、平均度量和极大平均度量引入复杂性函数的概念，并研究了具有有界复杂性的系统的性质.

(自治)动力系统中的复杂性研究已经非常丰富了[6-7].与此相应的，非自治动力系统中的系统复杂性也主要由熵来刻画，早有学者将自治系统中经典拓扑熵，经典测度熵以及Bowen维数熵等概念拓展到非自治系统中，并研究了他们之间存在的变分关系[8-12].参考文献[8]在定义非自治系统中拓扑熵的同时，也定义了渐近拓扑熵，并称当渐近拓扑熵大于零时，系统是拓扑混沌的.同样的，非自治系统中也面临着当熵为零时系统的复杂性的刻画的问题.一个自然的问题就是，在非自治系统中如何合适的引入有界复杂性的概念，是否可以得到与参考文献[5]类似的结论.

本文将在非自治离散系统中给出等度连续和平均意义下的等度连续性的概念，并证明非自治离散系统关于极大度量(极大平均度量)具有有界复杂性等价于该系统是(平均意义下)等度连续的.

2 基础知识

本章主要介绍非自治系统的定义与它的基本动力学性质.

2.1 非自治系统及等度连续性

定义1设(X,d)是一个紧度量空间，φ∶[0,+∞)×X→X是连续映射，且对∀x∈X，都有φ(0,x)=x，则称(X,φ)是非自治动力系统.

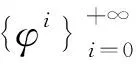
定义3设(X,Φ)是一个非自治离散动力系统，集合K⊂X称为是等度连续的，是指对∀ε>0，存在δ>0，使得当d(x,y)<δ的x,y∈X，都有d(φi(x),φi(y))<ε，i=0,1,2,….若K=X，则称(X,Φ)是等度连续的.

2.2 Hausdorff度量

定义4设K(X)是X的一个非空闭子集组成的集合，K(X)上的Hausdorff度量dH定义为

当(X,d)为紧度量空间时，(K(X),dH)也是紧的.设n∈，易见{A∈K(X)∶#(A)≤n}是K(X)的一个闭子集.

3 有有界拓扑复杂性的非自治离散动力系统

3.1 关于度量的拓扑复杂性

(X,Φ)是一个非自治离散动力系统，设n∈且x,y∈X，定义

对每个n∈，x,y,z∈X，容易验证：

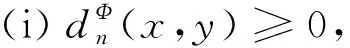
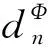
设K⊂X是一个紧集，n∈，ε>0.F⊂K称为K的(n,ε)张成集，若对任意x∈K都存在y∈F满足即

定义5用spanK(n,ε)表示K的具有最少元素的(n,ε)张成集中元素的个数，即

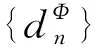
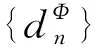
证⟸ 固定ε>0，由等度连续定义，对∀n∈+， ∀x,y∈K，存在δ>0使d(x,y)<δ时，都有d(φi(x),φi(y))<ε.又因为K是紧集，存在K的有限子集F，使则对∀n≥1，有故存在C=#(F)>0，使得

⟹ 相反，假设K不是等度连续的，即存在ε>0，对∀k≥1，存在xk,yk∈K,mk∈，使得d(xk,yk)<1/k时，有d(φmk(xk),φmk(yk))≥ε.不失一般性，假设k→∞时，xk→x0.则有x0∈K,故k→∞时有yk→x0.由三角不等式，对∀k∈，要么d(φmk(xk),φmk(x0))≥ε/2，要么d(φmk(yk),φmk(x0))≥ε/2.对∀k∈，总能找到x′∈{xk,yk}使d(φmk(x′),φmk(x0))≥ε/2，将x′记为xk，总可以假设d(φmk(xk),φmk(x0))≥ε/2，那么由定义，有

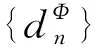
由Fn⊂K且K是紧的，则有F⊂K.又因为{A∈K(X)∶#A≤C}是闭集，#(F)≤C.对∀i∈， ∀x∈K，都存在zni∈Fni使得不失一般性的，可以假设i→∞时zni→z，故z∈F.

设

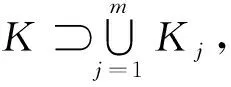
对于K中的序列{xk}，通过选取子列可以假设{xk}在某一个Kj中，又因为Kj是闭的，故x0∈Kj.注意到对

作为上述定理的推论，有下面的结论.

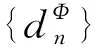
3.2 关于度量的拓扑复杂性

设(X,Φ)是一个非自治离散动力系统，设n∈且x,y∈X，定义

对每个n∈，x,y,z∈X，容易验证：

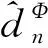
定义6设K⊂X是一个紧集，n∈，ε>0，定义

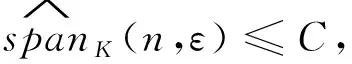
对任意n∈，x,y∈X，易知则若K关于有有界的拓扑复杂性，可得K关于也有有界的拓扑复杂性.

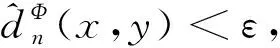
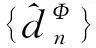
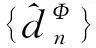
证⟸ 固定ε>0，由平均意义下等度连续定义，∀n∈+， ∀x,y∈K，存在δ>0使d(x,y)<δ时，都有由K的紧性，可找到K的有限子集F，使则对∀n≥1，由平均意义下等度连续，得故存在正整数C=#(F)>0，使得即K关于有有界拓扑复杂性.

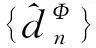
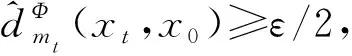
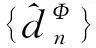
对任意i∈， ∀x∈K，都存在zni∈Fni使可假设i→∞时zni→z，故z∈F.

由定义可知，对∀u,v∈X，n∈，于是当nj≥ni时

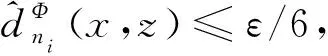
设

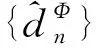
对于K中的序列{xk}，假设{xk}在同一个子序列Kj中，又因为Kj是闭的，x0∈Kj.注意到对

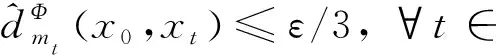
作为上述定理的推论，有以下结论.

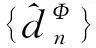
4 结 论

动力系统的复杂性是研究动力系统的重要组成部分，其中熵是非常重要的刻画系统复杂度的不变但.但在零熵系统中，一般的拓扑熵和测度熵就失去了它们的作用.本文从复杂度函数本身入手，证明了在极大度量和平均极大度量下，当非自治系统有有界复杂度时，它分别是等度连续和平均意义下等度连续的.由此，就可以研究熵为零时非自治系统的动力学性质.

致谢非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.