等距对应视角下的测地线

吴钰莹， 包图雅， 刘晓周

(内蒙古民族大学数理学院，内蒙古通辽 028000)

1 引 言

测地线是微分几何学中最基本的概念之一，也是几何学最基本的研究对象.曲面上的测地线在研究曲面中有着非常重要的地位，是曲面的一个重要指标.通过曲面上测地线的形状和性质，可以分析曲面的结构和性质.比如，球面上的测地线必在球面的大圆上[1].参考文献[2]通过给出一些特殊曲面上的测地线的几何特征，然后利用测地线的等距不变性，去分析螺面上测地线的大致分布情况.参考文献[3]通过研究椭球面与平面交线的几何性质，找到了椭球面上所有平面曲线类型的闭测地线.想了解测地线的形状和性质，求出测地线的方程也是一个有效途径.测地线的决定仅依赖于曲面的第一基本形式，当两个曲面成等距对应时，与测地线相对应的曲线也是测地线[4].本文是在两个曲面可以等距对应[5]的前提下，求出其中一个具有正交坐标网的曲面上的测地线方程，再通过等距对应求出了另一个曲面上的测地线方程.并利用数学软件画出了测地线的图像.

命题1[6]当曲面r=r(u,v)上的坐标网为正交网(F=0)时，刘维尔(Liouville)公式：

(1)

当kg=0时由刘维尔公式得到曲面上的测地线方程

(2)

其中θ表示曲线的切方向与ru的夹角，E,F,G是曲面r=r(u,v)的第一类基本量.

引理1[7]

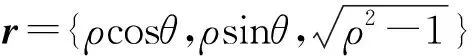
引理2[8]悬链面r={coshtcosθ,coshtsinθ,t}与正螺面r={ucosv,usinv,v}可建立等距对应u=sinht,v=θ.

引理3[9]抛物柱面r={2pu,2pu2,v}(p>0)与平面r={x,y,0}可建立等距对应.

2 主要结果

定理1螺旋面r={ucosv,usinv,u+v}上的测地线族方程为

其中c为非零常数.

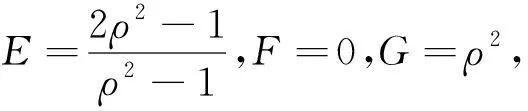
利用公式(2)求解旋转双曲面的测地线方程.由于

(3)

其中α(α∈[0,π])是曲线的切方向与rρ的夹角.

(4)

对(4)式第二式两边积分得

ln(sinα)=-lnρ+ln|c|(c为非零常数).

所以

因此由(4)式第一式可得

又因为当两个曲面成等距对应时，与测地线相对应的曲线也是测地线[4].所以螺旋面r={ucosv,usinv,u+v}上的测地线方程为

推论1当c=±1时，螺旋面r={ucosv,usinv,u+v}上的测地线方程为

其中ρ0是大于1的常数.

下面给出旋转双曲面与螺旋面上的测地线示意图(见图2).

图1 旋转双曲面，螺旋面上的测地线示意图

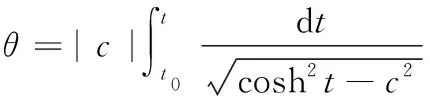
证正螺面的第一类基本量E=1,F=0,G=u2+1，所以曲面坐标网为正交坐标网.

利用公式(2)求解正螺面的测地线方程.由于

(5)

其中α(α∈[0,π])是曲线的切方向与ru的夹角.

因为当u=0时测地曲率为0，所以u=0这条曲线是测地线.

由于悬链面r={coshtcosθ, coshtsinθ,t}与正螺面r={ucosv,usinv,v}可建立等距对应u=sinht,v=θ[8].所以悬链面上的曲线方程为t=0.

又因为当两个曲面成等距对应时，与测地线相对应的曲线也是测地线[4]，所以悬链面r={coshtcosθ,coshtsinθ,t}上的测地线方程为t=0.

(6)

对(6)式第二式两边求积分，得

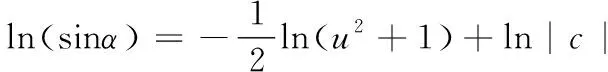
所以

因此由(6)式第一式可得

对上式两边分别求积分得正螺面r={ucosv,usinv,v}上的测地线方程为

由于悬链面r={coshtcosθ,coshtsinθ,t}与正螺面r={ucosv,usinv,v}可建立等距对应u=sinht,v=θ[8].所以悬链面上的曲线方程为

又因为当两个曲面成等距对应时，与测地线相对应的曲线也是测地线[4]，所以悬链面r={coshtcosθ,coshtsinθ,t}上的测地线方程为

推论2当c=±1时，悬链面r={coshtcosθ,coshtsinθ,t}上的测地线方程为

其中u0是常数.

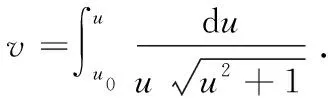
经过参数变换u=sinht,v=θ，得悬链面r={coshtcosθ,coshtsinθ,t}上的测地线方程为

下面给出正螺面与悬链面上的测地线示意图(见图2).

图2 正螺面，悬链面上的测地线示意图

定理3抛物柱面r={2pu,2pu2,v}(p>0)上的测地线族方程为

其中k,b为常数.

证设y=kx+b(k,b为常数)为平面上的一条直线，那么这条直线一定是平面上的测地线[6].

因为抛物柱面r={2pu,2pu2,v}(p>0)与平面r={x,y,0}可建立等距对应[9]

所以抛物柱面的曲线方程为

又因为当两个曲面成等距对应时，与测地线相对应的曲线也是测地线[4]，所以抛物柱面r={2pu,2pu2,v} (p>0)上的测地线方程为

下面给出平面与抛物柱面上的测地线示意图.

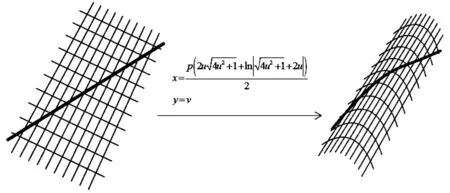
图3 平面、抛物柱面上测地线的示意图

3 结 论

本文利用曲面之间的等距对应求出了曲面上的测地线方程，并且为不具有正交坐标网的曲面求解测地线方程提供了新思路，计算方法简洁明了，容易理解.但是找到等距对应的曲面是不容易的，目前已知的是几个特例.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.