矩阵广义逆与方程的解

翟佩佩， 石欣侗， 魏俊潮

(扬州大学数学科学学院，江苏扬州 225002)

1 引 言

矩阵是代数学的一个主要研究对象,矩阵广义逆的概念最早由Fredholm于1903年提出[1],其在解线性方程组、矩阵方程组中有着广泛的应用.

Mn(C)表示复数域上全体n阶矩阵的集合.设A∈Mn(C),用AH表示矩阵A的共轭转置矩阵.

若A2=A,则称A为幂等矩阵[2].幂等矩阵的研究是矩阵理论中一个重要研究内容.

若存在复矩阵X,满足条件

AXA=A, XAX=X, AX=XA，

则称A是群可逆矩阵,并称X是A的群逆矩阵.并不是每个矩阵都是群可逆矩阵.一个复矩阵A是群可逆矩阵当且仅当rank(A)=rank(A2).若A是群可逆矩阵,则其群逆矩阵是唯一确定的,通常记为A#[3].

如果AHA=AAH,则称A是正规矩阵[4].众所周知，一个n阶复矩阵A可酉对角化当且仅当A是正规矩阵.

若AT=A,其中AT表示矩阵A的转置矩阵,则称A是对称矩阵[5].

由于矩阵广义逆有着广泛的应用,所以本文通过深入研究适当的矩阵方程,探讨所得矩阵方程在给定集合中解的存在性对矩阵广义逆性质的影响.在本文中以参考文献[6]的等价条件,参考文献[5]的XAX=A矩阵方程的解的讨论和参考文献[7]的矩阵方程AX=A+X的构造为灵感,并运用到上述基本概念,主要研究一些特殊矩阵方程解存在的条件，通过深入研究方程AX=A+X,对于参考文献[7]与本文重复的定理,本文给出了一种新的证法,并对该方程进行解析,在参考文献[7]的基础上进行推广研究,得到了更多好的定理,使矩阵方程AX=A+X的研究更加全面.

关于矩阵方程AX=A+X的推广研究在本文的讨论中还需要引申参考文献[7]中的结论.

引理1设A∈Mn(C),则矩阵方程AX=A+X有解当且仅当En-A为可逆方阵.此时X=En-(En-A)-1.

2 主要成果

定理1设A∈Mn(C),则下面的矩阵方程有幂等矩阵解当且仅当A为幂等矩阵且En-A为可逆矩阵

AX=A+X.

(1)

证必要性.假设矩阵方程(1)有幂等矩阵解,设解为X=B,则由引理1知En-A为可逆矩阵且 AB=A+B,右乘B,注意到B是幂等矩阵,故有AB=AB+B,因此B=O,从而

O=AB=A+B=A+O=A,

于是A是幂等矩阵.

充分性.由于En-A为可逆矩阵,故由引理1知方程(1)有解,设解为X=B, 则AB=A+B,由于A为幂等矩阵,故左乘A得AB=A+AB,从而A=O,于是B=AB-A=O,故B为幂等矩阵,即方程(1)有幂等矩阵解.

称形如KEn(0≠k≠1)的矩阵为真纯量矩阵.

定理2矩阵方程(1)有真纯量矩阵解当且仅当A为真纯量矩阵.

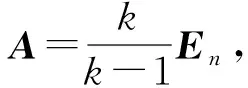
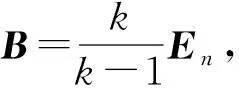
定理3矩阵方程(1)有幂零矩阵解当且仅当A为幂零方阵.

证必要性.假设矩阵方程(1)有幂零矩阵解X=B,即∃m∈,Bm=O.由引理1知(A-En)(B-En)=En,所以(B-En)(A-En)=En,因此

(A-En)(B-En)=(B-En)(A-En),

可得到AB=BA,由方程AB=A+B,知A=(A-En)B,于是

A2=(A-En)BA=(A-En)AB=(A-En)(A-En)BB=(A-En)2B2,

重复这个过程可得Am=(A-En)mBm=O.因此A为幂零方阵.

充分性.假设A为幂零方阵,则∃k∈,Ak=O,所以En-A为可逆矩阵,故由引理1知方程(1)有解,设解为X=B,则AB=A+B,则可知B=A(B-En),于是

B2=A(B-En)B=AB(B-En)=AA(B-En)(B-En)=A2(B-En)2,

重复上述过程可得Bk=Ak(B-En)k=O.因此矩阵方程(1)有幂零矩阵解.

定理4矩阵方程(1)有对称方阵解当且仅当A为对称方阵且En-A可逆.

证必要性.假设矩阵方程(1)有对称方阵解X=B,由引理1知En-A为可逆矩阵且AB=A+B,两边同时转置得BTAT=AT+BT,即BAT=AT+B,从而(B-En)(AT-En)=En,由引理1知(A-En)(B-En)=En,由于可逆矩阵的性质,逆矩阵是唯一的,所以AT-En=A-En,故A为对称方阵且En-A可逆.

充分性.假设A为对称方阵且En-A可逆,故由引理1,方程(1)有解,设解为X=B,则AB=A+B,两边同时转置得BTAT=AT+BT,即BTA=A+BT,从而(BT-En)(A-En)=En,由引理1知(A-En)(B-En)=En,由于可逆矩阵的性质,逆矩阵是唯一的,所以BT-En=B-En,因此矩阵方程(1)有对称方阵解.

定理5设C为n阶方阵,则矩阵方程(1)有与C可交换的矩阵解当且仅当A与C可交换且En-A可逆.

证必要性.假设矩阵方程(1)有与C可交换的矩阵解X=B,则由引理1知En-A为可逆矩阵且BC=CB,则

ACB=ABC=AC+BC,

所以AC(B-En)=BC,又

CAB=CA+CB=CA+BC,

所以CA(B-En)=BC,又因为(A-En)(B-En)=En，所以B-En可逆,则

AC=BC(B-En)-1=CA.

充分性.假设A与C可交换且En-A可逆,由于En-A可逆,故由引理1,方程(1)有解,设解为X=B,则AB=A+B,于是

CAB=ACB=CA+CB,

所以(A-En)CB=CA,故CB=(A-En)-1CA,又ABC=AC+BC,所以(A-En)BC=AC,故BC=(A-En)-1AC,由于AC=CA,故BC=CB,所以矩阵方程(1)有与C可交换的矩阵.

推论1若n阶方阵A,B满足AB=A+B,则(i) AB=BA； (ii) rank(A)=rank(B).

证(i)这是定理3的证明的一部分；

(ii) 因为AB=A+B,所以

rank(A)=rank(AB-B)=rank((A-En)B),

又因为由引理1知A-En可逆，所以rank((A-En)B)=rank(B),所以rank(A)=rank(B).

定理6矩阵方程(1)有群可逆矩阵解当且仅当A为群可逆矩阵且En-A可逆.

证必要性.设X=B为方程(1)的群可逆矩阵解,则由引理1知En-A可逆且AB=A+B,右乘B得AB2=AB+B2,从而(A-En)B2=AB,由于B为群可逆阵,则rank(B)=rank(B2),因为A-En可逆,则

rank(B2)=rank((A-En)B2)=rank(AB),

从而rank(B)=rank(AB),故由推论1知rank(A)=rank(AB),因为A2B=A2+AB,所以A2(B-En)=AB,因为B-En可逆,所以

rank(AB)=rank(A2(B-En))=rank(A2),

从而rank(A)=rank(A2),故A为群可逆矩阵.

充分性.由于En-A可逆,故由引理1,方程(1)有解X=B,即AB=A+B,从而En-B可逆且A2B=A2+AB,从而A2(B-En)=AB,从而rank(A2)=rank(AB),因为AB2=AB+B2,所以(A-En)B2=AB,所以

rank(B2)=rank((A-En)B2)=rank(AB)=rank(A2),

因为A是群可逆矩阵,则rank(A)=rank(A2),又由推论1,rank(A)=rank(B),因此rank(B)=rank(B2),从而B是群可逆矩阵.

定理7方程(1)有可对角化矩阵解当且仅当A可对角化且En-A可逆.

证必要性.设(1)有可对角化矩阵解X=B,则由引理1,En-A可逆,且AB=A+B,从而En-B可逆且(En-B)-1=En-A,设

则

所以

故

因此A可对角化且En-A可逆.

充分性.假设A可对角化,且En-A可逆,由引理1知,方程(1)有解.设X=B,

则

所以

故

因此方程(1)有可对角化矩阵解.

命题1设A,B为n阶可逆方阵，则下列条件等价:

(i) AB=A+B；

(ii) A-1+B-1=En；

(iii) A=En+AB-1；

(iv) B=En+A-1B.

证(i)⟹(ii).因为AB=A+B,等式两边同时左乘A-1,右乘B-1,则

A-1ABB-1=A-1(A+B)B-1,

可得到A-1+B-1=En,(ii)得证.

(ii)⟹(iii).因为A-1+B-1=En,等式两边同时左乘A,则

A(A-1+B-1)=AEn,

可得到A=En+AB-1,(iii)得证.

(iii)⟹(iv).因为A=En+AB-1,等式两边同时右乘B,则

AB=(En+AB-1)B=B+A,

可得到

B=EnB=(A-1A)B=A-1AB=A-1(A+B)=En+A-1B,

(iv)得证.

(iv)⟹(i).因为B=En+A-1B,等式两边同时左乘A,则

AB=A(En+A-1B)=A+B,

(i)得证.

命题2设A,B为整矩阵(即元素全为整数的矩阵)且AB=A+B,则|A|=|B|或|A|=-|B|.

证由于AB=A+B,故(A-En)(B-En)=En,因为A,B为整矩阵，故A-En,B-En也为整矩阵,从而|A-En|,|B-En|为整数,又

|A-En||B-En|=|(A-En)(B-En)|=|En|=1,

所以

|A-En|=|B-En|=1 或 |A-En|=|B-En|=-1,

因为

A=AB-B=(A-En)B, B=AB-A=A(B-En),

所以

|A|=|A-En||B|, |B|=|A||B-En|,

所以|A|=|B|或|A|=-|B|.

注1 从引理1可知,矩阵方程(1)有解时,解是唯一的,故有注2.

注2 矩阵方程(1)有反对称方阵解不能推出A是反对称矩阵，反之亦然，反例如下.

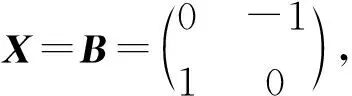
显然A不是反对称矩阵，反之亦然.

定理8矩阵方程(1)有正规矩阵解当且仅当A为正规矩阵且En-A可逆.

证必要性.假设AX=A+X有正规矩阵解,设为X=B,则AB=A+B,故

(En-A)(En-B)=En,

En-A可逆,因为B正规,所以BBH=BHB,由定理5知ABH=BHA,从而BAH=AHB,再由定理5知AAH=AHA,故A为正规矩阵.

充分性.由于En-A可逆,则AX=A+X有解X=B,即AB=A+B,从而BA=B+A,即矩阵方程BX=B+X有正规矩阵解,从而由必要性的证明知B为正规矩阵.

3 结 论

文中通过对矩阵方程AX=A+X的研究,不断纠错矩阵方程、修改矩阵方程、变形矩阵方程时矩阵所呈现出来的广义逆性质,得到了一系列存在特殊解的等价条件的相关定理,并在研究矩阵方程AX=A+X的过程中也发现了AB=A+B此等式的一些相关性质,使矩阵方程AX=A+X的研究更加全面,也为研究矩阵方程提供了思路.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.