关于正切函数的一个不等式的注记
2022-11-17李平
李 平
(中国科学技术大学数学科学学院,合肥 230026)
1 引 言
在绝大多数数学分析或微积分类的教材中(见参考文献[1-3]), 在函数极限部分为了证明
这个重要极限都应用了如下不等式:
(1)

图1

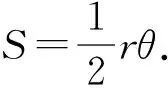
2 不等式的证明
首先是不等式
(2)

图2
这个不等式几何上反映的是圆中一段弧的长度大于所对应的弦的长度.
如图2所示, 在单位圆中,A为圆心.设B和C是圆周上两点, 圆心角∠BAC=2x, 因而圆弧的长为2x.过B和C的两条切线交于D点.分别连接A,D两点, 及B,C两点, 线段AD交BC于E点, 交圆弧BC于F点.则线段AD垂直于BC, 线段AB垂直于BD, 线段AC垂直于CD, 而且∠BAD=∠CAD=x, 因而线段BC长为2sinx.因为弧长大于对应的弦的长, 所以,2x>2sinx. 即sinx 再考虑不等式 (3) 如图2所示, 过F点作圆的切线, 交线段BD于G点, 交线段CD于H点.因BD=CD=tanx, 所以圆外切折线L1={B,D,C}的长为s1=2tanx.记圆外切折线L2={B,G,F,H,C} 的长度为s2.因为DG+DH>GH, 所以s1>s2.接着在扇形BAF和扇形CAF中考虑,按照同样的作法, 可以得到圆外切折线L3, 其长s3 图3 命题1光滑凸曲线段的起点A和终点B处的切线在曲线凸出的一侧相交于C点, 则直线段AC与BC的长度之和大于这条曲线段的长度. 证如图3所示在曲线AB的中点D处的切线交线段AC于E点,交线段BC于F点.因为曲线是凸的,所以E在A和C之间,F在B和C之间.因为CE+CF>EF,所以折线ACB的长s1大于折线AEDFB的长s2. 再在曲线段AD的中点G作曲线的切线,交AE于H,交EF于I,在曲线段BD的中点J作曲线的切线,交DF于K,交BF于L,则折线AEDFB的长s2大于折线AHGIDKJLB的长s3.继续这一过程,可得一列逼近曲线AB的折线,且这一列折线的长度是递减的.根据长度泛函具有下半连续性(见参考文献[4],Prop.2.3.4),可知折线ACB的长s1大于曲线AB的长.证毕. 根据命题1和弧长计算公式可以得到下面的结论: 命题2设f(x)在区间[0,a)上有二阶连续导数,满足f(0)=f′(0),且f″(x)>0 (0 从前面的讨论可知不等式sinx 本文从数量关系发现它所对应的几何意义,从几何的特性发现数量关系一个证明,并在几何上给予推广,又将推广的几何结论回到推广的数量关系上.这正是数与形的一种结合.在微积分等学科中很多分析上的结论都有其几何意义.把握好这些几何意义对于理解分析上的结论就很有帮助,也有利于从几何上阐发,从而进一步拓广分析的结论. 致谢感谢审稿人的仔细审稿以及给予的建议!3 几何上的推广

4 结 论
