基于图拉普拉斯的多标签类属特征选择

吴 君, 黄 睿

(上海大学通信与信息工程学院, 上海 200444)

在传统的单标签学习框架中, 每个样本只对应一种标签. 然而, 在现实生活中, 大部分对象都表现为多语义性[1-2], 即一个样本同时对应多种标签. 因此, 多标签学习模型更具实际应用价值, 已经在图像标注[3]、文本分类[4]、音乐情感分类[5]等领域获得应用.

与单标签学习一样, 多标签学习也会受到“维度灾难”的影响, 尤其在多标签分类问题中,大量冗余特征不仅会增加计算复杂度, 也会降低分类器的性能. 通过特征选择, 去除无关冗余特征, 基于特征子集进行分类是解决该问题的有效方法. 目前, 已有很多标签特征选择算法[6-12], 但多数算法忽略了标签与特征之间存在的内在联系, 只是基于相同的特征子集对所有标签进行分类. 事实上, 对于不同的标签, 存在一些最能体现该标签内在属性的特征, 这些特征对相应标签具有更强的判别能力, 被称为类属特征(label-specific features). 基于类属特征的多标签分类表现出了更好的性能, 如何构建类属特征已成为相关领域的研究热点之一[13-17].

Zhang 等[13]最早提出了基于类属特征的多标签学习(multi-label learning with labelspecific features, LIFT)算法, 该算法将数据的原始特征转换为数据与正负样本聚类中心的距离, 以此来构建类属特征. 文献[15-16]在LIFT 基础上引入标签相关性, 分别提出基于标签相关性的类属属性多标签分类算法(label-correlation based multi-label classification algorithm with label-specific features, CLLIFT)[15]和利用聚类集成的类属特征多标签学习(multi-label learning with label-specific features via clustering ensemble, LIFTACE)算法[16]. 上述算法采用特征变换的方式获得类属特征, 改变了特征属性的固有含义. Huang等[14]则提出了一种类属特征学习(learning label-specific features, LLSF)算法, 该算法通过优化具有稀疏正则项的线性分类器确定类属特征. 但LLSF 得到的类属特征子集规模较大, 特征间冗余较多. 文献[17]基于线性判别分析思想改进LLSF 的目标函数, 提出了联合特征选择和分类的多标签学习(joint feature selection and classification for multi-label learning, JFSC)算法[17].

LLSF 和JFSC 算法都假定数据与类别标签间存在线性关系, 直接对标签进行稀疏回归学习来确定系数矩阵. 但事实上, 大部分数据都不满足线性可分性, 因此该假设是不合理的. 本工作结合流形学习和稀疏回归, 认为具有较高判别性的特征应尽可能保持数据的低维结构特性[18], 由此提出一种基于图拉普拉斯的多标签类属特征选择(multi-label label-specific feature selection based on graph Laplacian, LSGL)算法. 首先利用图拉普拉斯获取数据的低维流形结构, 再对流形结构的稀疏回归计算系数矩阵, 确定类属特征.

1 LSGL 算法

1.1 构建低维嵌入

设由N个样本构成的数据集为X= [x1,x2,··· ,xN]∈RD×N, 标签集合为L={l1,l2,··· ,lC}, 数据集对应的逻辑型类别标签集为Y= [y1,y2,··· ,yN]T∈{0,1}N×C,C为类别标签个数.xn ∈RD对应的标签为yn= [yn1,yn2,··· ,ynC]∈{0,1}C, 1 表示样本与标签相关, 0 表示样本与标签无关.

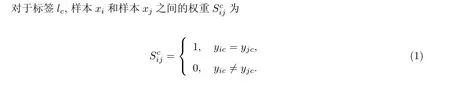
对于同一标签, 如果两个样本都是正样本或负样本, 那么它们之间的权重为1, 反之为0. 由此,可以得到对于标签lc的邻接矩阵Sc, 进而可以求得度矩阵Dc和拉普拉斯矩阵Lc[19],

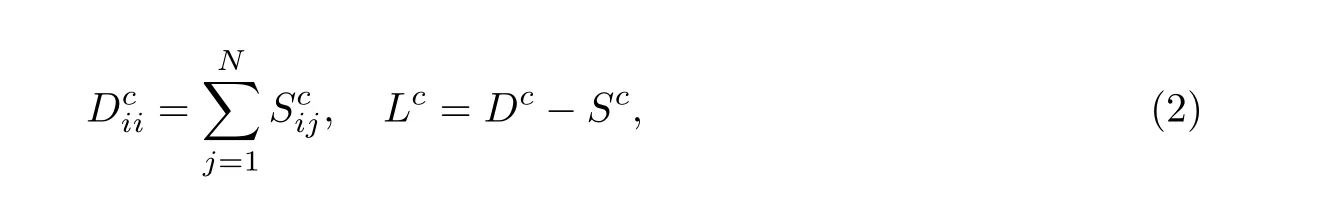
式中: 矩阵Dc为对角阵, 对角元素为Sc每列元素之和. 数据的低维流形可以通过求解以下广义特征值问题得到,

取前K个最小特征值对应的特征向量构成原始数据对于标签lc的低维嵌入[20],

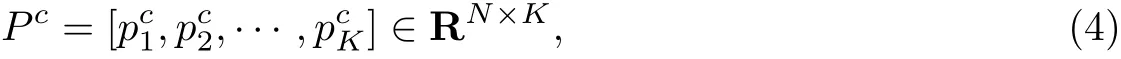
式中:K是低维嵌入的维数. 在文献[21]提出的非监督谱聚类算法中, 低维流形的维数设置为数据的聚类簇数. 在LSGL 算法中, 对于每个标签, 数据只可能具有该标签或不具有该标签,这是一个二分类问题, 可以认为数据由两个类簇组成, 由此将K设置为2.

1.2 稀疏特征选择

对于标签lc, 从数据空间到流形空间的投影矩阵Wc=[w1,w2]可通过优化以下目标函数获得,

式中:‖·‖2和‖·‖1分别表示向量的1 范数和2 范数;pck表示pc的第k列;wk为d维向量, 表示每个特征在相应维度上的权重, 而由于K= 2, 故低维嵌入实际上是一个二维空间,即k ∈{1,2}, 利用wk将原始数据映射到这个二维空间. 式(5)是一个典型的套索即最小绝对值收敛和选择算子(least absolute shrinkage and selection operator, LASSO)回归问题,l1正则化项保证了特征权重wk的稀疏性. 使用最小角回归(least angle regression, LARS)算法[22]获得wk.

投影矩阵Wc ∈Rd×2的每行表示对应特征在低维流形上的权重. 对于第d个特征, 定义重要度评分为

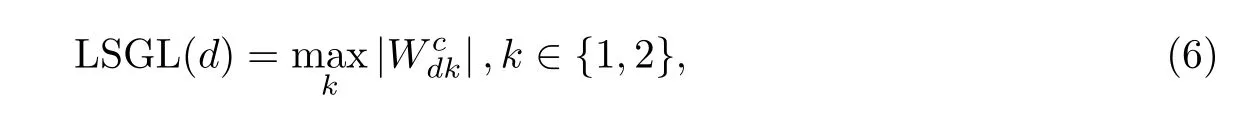
式中:Wcdk为Wc的第d行、第k列元素. 特征评分值越大, 表明该特征越重要.

对每个标签计算投影矩阵, 可获得相应的类属特征, 再利用类属特征对每个标签构建二分类器进行训练和预测. LSGL 算法的完整流程如表1 所示.

表1 LSGL 算法Table 1 LSGL algorithm

2 实 验

2.1 数据集

为了评估所提出算法的性能, 在5 个多标签数据集上进行特征选择和分类实验, 数据集均来自Mulan 数据库(http://mulan.sourceforge.net/datasets-mllc.html), 详细信息如表2 所示.

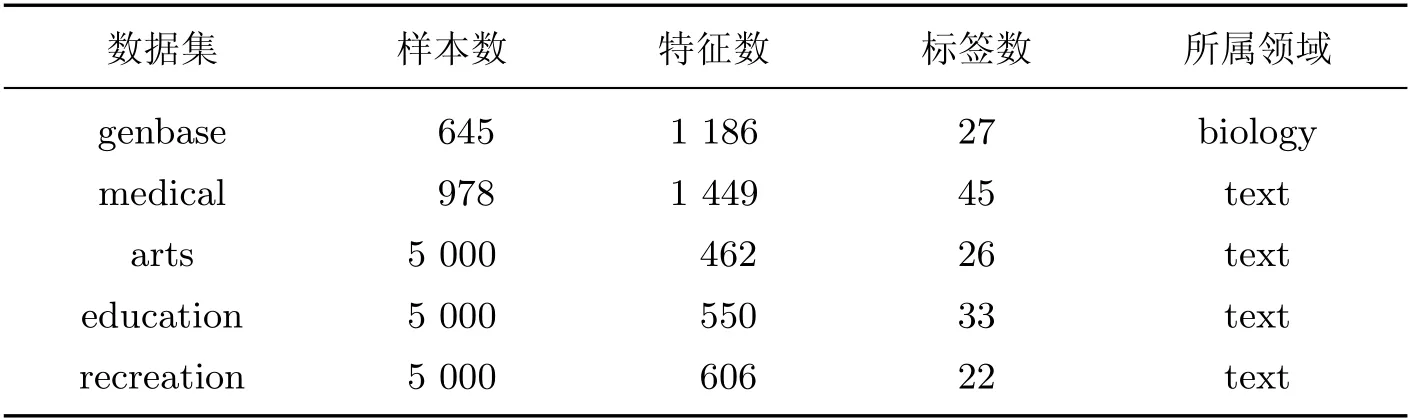
表2 数据集信息Table 2 Data information

2.2 实验设置

本工作选取7 个多标签学习算法作为对比算法, 并利用5 种评价指标衡量不同算法的性能.

2.2.1 对比算法

7 种多标签学习算法分别为二元关联法(binary relevance, BR)[23]、LIFT[13]、LLSF[14]、类属特征学习-二元支持向量机(learning label-specific features-binary support vector machine, LLSF-BSVM)[14]、LASSO[11]、鲁棒特征选择(robust feature selection, RFS)[12]和利用稀疏性的子特征发现(sub-feature uncovering with sparsity, SFUS)[8], 可划分为如下3 类.

(1) BR: 基于特征全集, 将多标签学习问题转换为多个二分类问题进行分类, 实验结果可作为比较基准.

(2) LIFT、LLSF、LLSF-BSVM 是基于类属特征的多标签学习算法, 其中LIFT 通过特征映射来构建类属特征; LLSF 和LLSF-BSVM 利用特征选择得到类属特征, 但前者直接基于权重矩阵使用线性回归模型进行类别预测, 后者则利用权重矩阵选择类属特征后, 再利用分类器进行训练和预测.

(3) LASSO、RFS、SFUS: 传统的多标签特征选择算法, 即对所有类别采用相同特征子集进行分类. LASSO 是基于l1正则化的特征选择方法; RFS 是通过最小化损失函数和正则化项的l2,1范数进行特征选择; SFUS 则融合了稀疏特征选择和计算共享特征子空间两种思想.

本工作所提算法LSGL 不需要设置参数, 7 种对比算法涉及的参数均使用相应文献中的建议参数. 此外, 除LLSF 算法外, 其余算法均使用二元支持向量机库(library for binary support vector machines, LIBSVM)[24]作为基分类器, 采用线性核, 参数C=1.

2.2.2 评价指标

本工作采用5 种广泛使用的多标签学习评价指标来衡量算法性能.

假设测试数据集T={(xi,Yi)|1 ≤i≤t},C个二分类模型(f1,f2,··· ,fC). 算法对数据xi预测的标签集合为Y′i, 则各评价指标的定义如下.

汉明损失(Hamming loss, HL): 考察样本的标签被误分类的情况.

式中: Δ 表示两个集合之间的对称差.

1-错误率(one-error, OE): 考察样本的预测标签中排名最靠前的标签不是相关标签的情况.

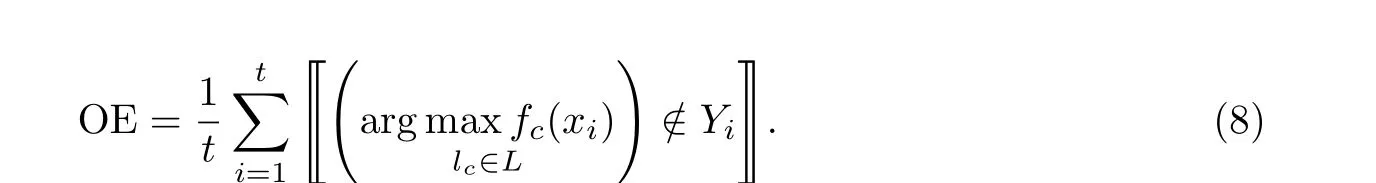
对于任意π, 当π成立时, 〚π〛取值为1; 当π不成立时, 〚π〛取值为0. 覆盖率(coverage, CV):考察在样本的预测标签排序中, 找到样本的所有相关标签所需步骤数.

式中:R(xi,lc)={lj|rank(xi,lj)≤rank(xi,lc),lj ∈Yi}.

以上5 种评价指标的取值范围均为0～1. 平均精度指标取值越大, 则分类性能越好; 而其余4 个评价指标则相反.

2.3 实验结果及分析

所有实验均采用5 折交叉验证, 取平均值作为每次实验的结果. 需要指出的是, LLSFBSVM 算法无法指定类属特征个数, 并且不同标签的类属特征个数也不同. 为方便比较, 本工作统计了LLSF-BSVM 算法在不同数据集上对不同类别标签选取的平均类属特征数, 将其作为LASSO、RFS、SFUS 这3 种传统特征选择算法的特征子集规模. 对于LSGL 算法,选择的类属特征个数与LLSF-BSVM 算法选择的平均类属特征个数保持一致. 表3 给出了LLSF-BSVM 算法在不同数据集上的平均类属特征个数.

表3 LLSF-BSVM 算法得到的平均类属特征个数Table 3 Average number of lable-specific features by LLSF-BSVM algorithm

表4～8 给出了包括本工作所提出算法在内的8 种算法分别在5 个数据集上的性能指标,其中↓(↑)表示该指标值越小(大), 分类性能越好, 指标值后括号中的数字表示每个算法在相应性能指标上的排名. 此外, “Rank”列表示算法在各评价指标上的平均排名, 值越小则性能越好.

表4 genbase 数据集的实验结果Table 4 Results on genbase data set

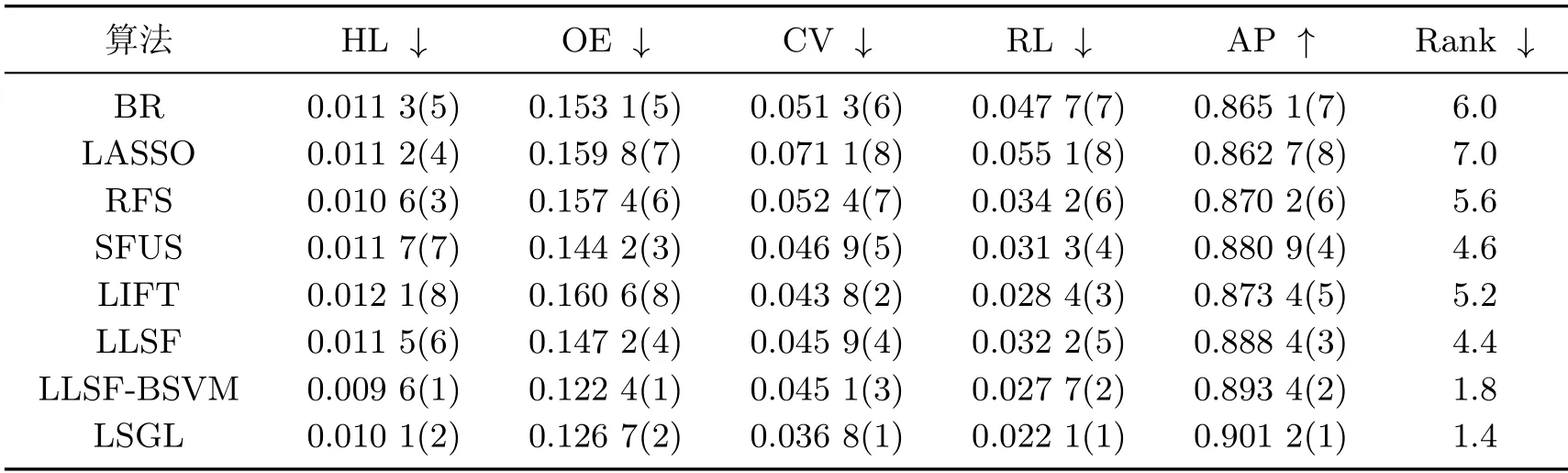
表5 medical 数据集的实验结果Table 5 Results on medical data set

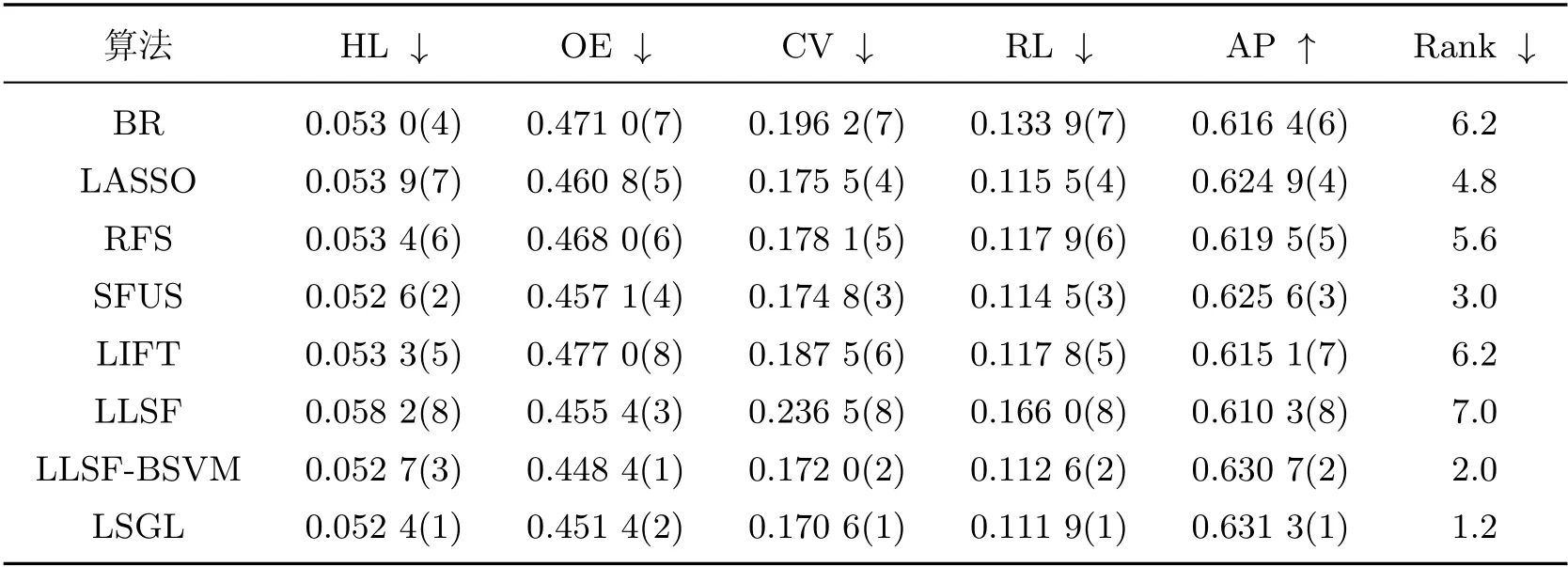
表6 arts 数据集的实验结果Table 6 Results on arts data set

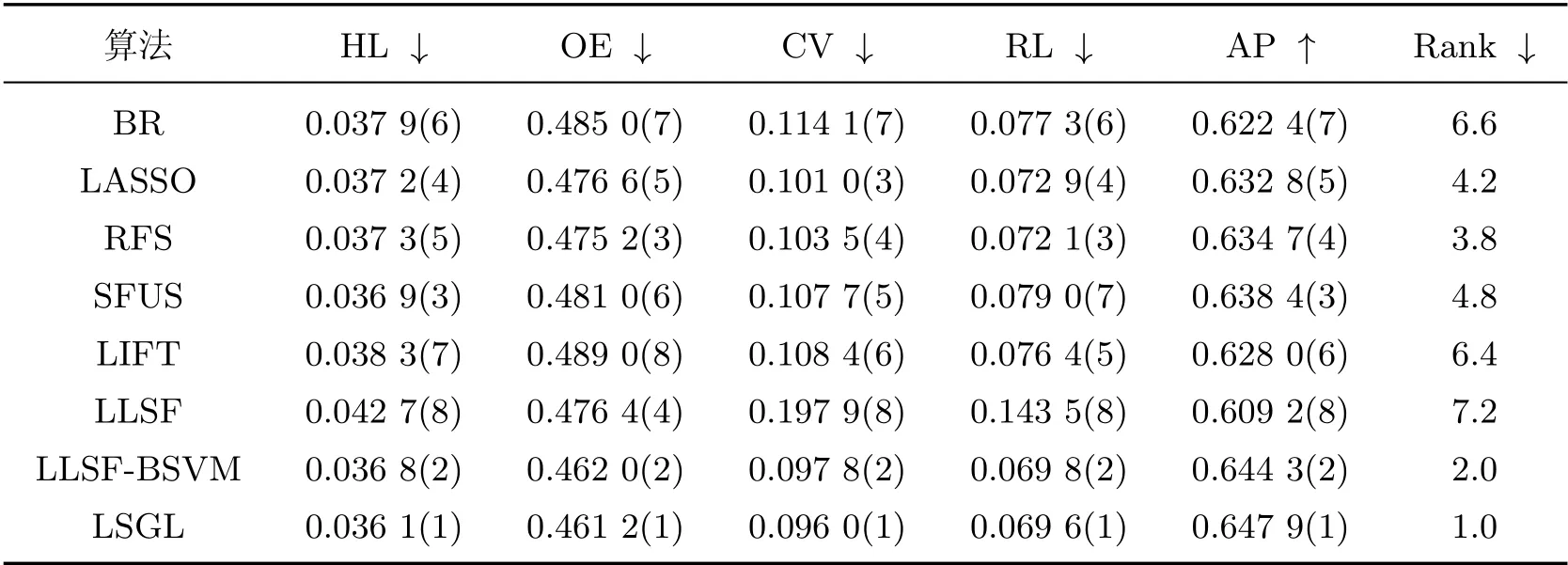
表7 education 数据集的实验结果Table 7 Results on education data set

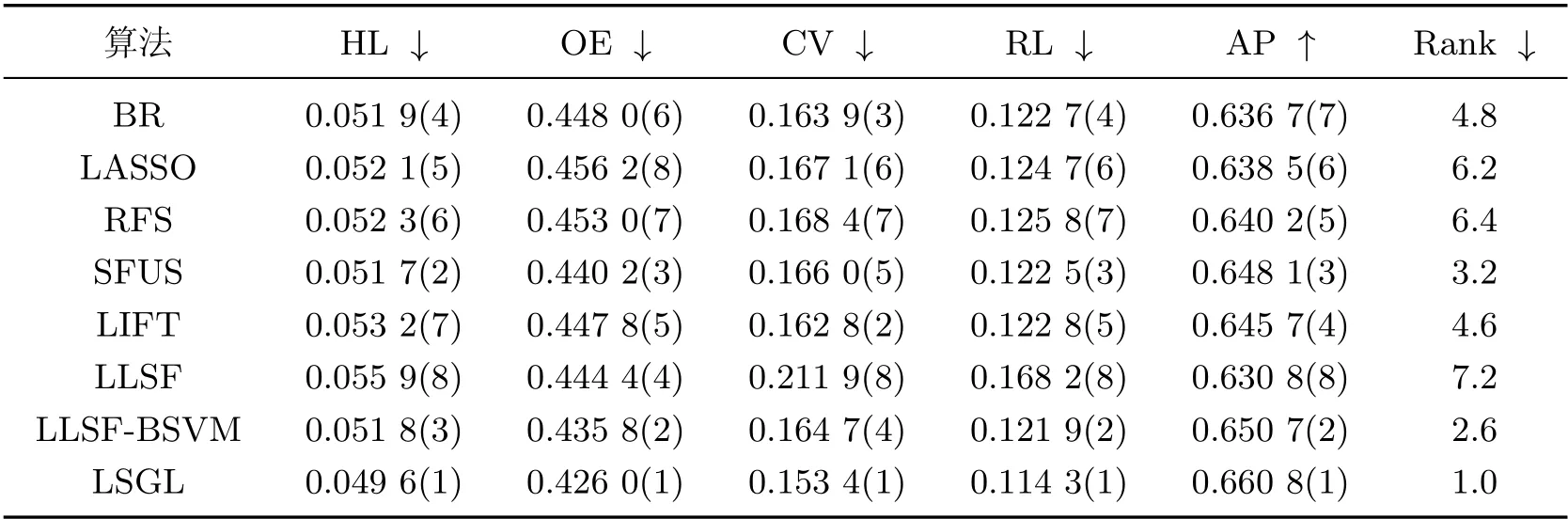
表8 recreation 数据集的实验结果Table 8 Results on recreation data set

从表4～8 的实验结果可以看出, 本工作所提算法LSGL 取得了较好的分类性能. 观察“Rank”列可以发现, LSGL 算法在所有数据集上取得了最高平均排名. 具体而言, 对于5 个数据集和5 种评价指标, 总共25 种情况下, LSGL 算法在其中的21 种情况排名第一, 4 种情况排名第二, 这充分说明了LSGL 算法在分类性能上的优越性. 根据不同数据集上的平均排名, 8 种算法的性能排序为LSGL＞LLSF-BSVM＞SFUS＞LIFT＞BR＞LLSF＞LASSO＞RFS.LIFT、LLSF-BSVM 和LSGL 使用了类属特征, 因此整体排名要高于没有使用类属特征的算法BR、LASSO、RFS 和SFUS, 这说明在多标签分类中引入类属特征的必要性. 值得一提的是, 虽然LLSF 算法使用了类属特征, 但分类性能较差, 原因可能是其他算法均使用SVM 作为基分类器, 而LLSF 算法直接使用线性回归模型进行预测, 影响了分类精度. 在LIFT、LLSF-BSVM 和LSGL 这3 种算法中, LIFT 算法的排名远低于另外两种算法, 原因可能在于LIFT 算法通过特征映射来构建类属特征, 从而损失了原始特征空间的一些有用信息.LLSF-BSVM 和LSGL 算法均是通过特征选择来获得类属特征, 但后者性能更优, 说明基于图拉普拉斯的特征评价准则能选择出更具有判别力的特征.

图1(a)～(e)以AP 指标为例, 给出了LSGL、LASSO、RFS 和SFUS 这4 种多标签特征选择算法的性能在不同特征子集规模下的变化情况, 其中BR 算法直接使用原始特征进行分类, 可作为比较基准. 表9 给出了各数据集的特征子集规模.

表9 选择特征的个数Table 9 Number of selected features

图1 在不同数据集上的特征选择结果Fig.1 Results of feature selection on different data sets

从图1(a)～(e)的实验结果可以发现, 在不同的特征子集规模下, LSGL 算法都优于对比算法, 表现出了更优异的性能. 在genbase 数据集上, 当选择10 个特征时, LSGL 算法的性能要明显优于其他算法, 并且超过了BR 基准算法. 随着选择特征数增多, 其他算法的性能逐渐接近甚至超过了LSGL 算法, 但整体差距很小. 在medical 数据集上, LSGL 算法的性能始终优于其他算法, 尤其是选择的特征数较少时差距较为明显, 且始终高于Baseline, 表明类属特征选择能够在选择较少特征的同时取得更优异的性能. 在arts、education 和recreation 这3 个数据集上, 算法性能随特征数变化的趋势比较类似, 因此一并进行分析. 可以看到, LSGL 算法的性能曲线始终位于最上方, 且与其他算法保持着一定的距离, 而随着特征数的增多, LSGL算法的性能也超越了Baseline.

3 结束语

与单标签学习一样, 多标签学习同样面临着“维数灾难”的问题, 使用特征选择可以有效消除冗余信息. 另一方面, 对于每个标签, 都具有最能反映其标签特性的特征, 即类属特征. 本工作提出的LSGL 算法, 通过对每个标签构建样本邻接矩阵, 用拉普拉斯特征映射方法得到数据的低维嵌入, 再优化带有稀疏正则项的目标函数, 求得从数据空间到嵌入空间的投影矩阵, 通过矩阵系数分析对特征重要度进行评分, 由此得到每个标签的类属特征. 在5 个公共多标签数据集上的特征选择和分类实验表明, 相比7 种对比算法, LSGL 算法的性能优势明显.

LSGL 算法在进行类属特征时没有考虑标签之间的相关性, 因此后续研究将关注如何在构建类属特征的同时引入标签相关性, 从而进一步提升分类性能.