电荷比特的超强藕合实现及量子态转移

俞 静, 周 沫, 黄堂友, 郝敏佳, 陈 玺

(上海大学理学院, 上海 200444)

量子计算领域始于19 世纪80 年代. 基于量子的相干叠加和纠缠特性, 量子计算被认为是有望延续摩尔定律[1], 克服经典计算能力瓶颈的新型计算模式[2]. 多年来, 实现量子计算的实验平台呈多样性发展, 如超导量子电路[3-7]、离子阱体系[8-9]、光学系统[9-11]等, 其中超导量子电路因其高集成性、可操控性和设计灵活性, 成为了实现量子计算的主流平台. 用于量子计算的超导电路系统可以分为两类: 一类是由约瑟夫森结(Josephson junction, JJ)构成的宏观电路[12-13], 具备高非谐性, 可以模拟原子系统的能谱, 构成量子计算的基本单元, 即量子比特; 另一类是由线性元件(电容器、电感器)组成的微波谐振子[14-16], 构成与量子比特相互作用的“光子源”.

超导量子电路平台的快速发展推动了电路量子电动力学(circuit quantum electrodynamics, cQED)领域的研究[7,17], 使得人们能够在宏观量子系统中研究量子光学和量子信息处理. 首先, 与腔量子电动力学(cavity quantum electrodynamics, CQED)中使用的三维微波腔[18]不同, cQED 平台中的谐振子是一维系统, 能够实现更强的电磁场真空涨落. 其次, 由于cQED 系统结构和参数的可塑性强, 人们可以设计人造原子, 从而实现比自然原子更大的原子电偶极矩和磁偶极矩[19-20]. 因此, 在cQED 系统中, 通过将人造原子与谐振子耦合, 可以实现在自然系统中无法达到的光与物质耦合强度, 如超强耦合(ultra-strong coupling, USC)区间[19-22]、深度强耦合(deep-strong coupling, DSC)区间[23-24]等. 此外, 随着光与物质耦合强度的不断突破, 关于“人造原子与微波谐振腔之间是否存在基本的耦合极限”这一问题也受到了广泛关注, 并迅速成为cQED 领域和量子光学领域的研究重点之一.

本工作围绕如何在超导量子电路中, 实现光与物质的USC 这一问题展开研究. 首先, 研究了单个电荷量子比特, 即库珀对盒子(Cooper-pair box, CPB)[3-4]与LC 谐振子耦合的超导电路, 并通过定义耦合比率来量化耦合强度与约瑟夫森能量和LC 谐振子阻抗的依赖关系. 其次, 通过优化目标函数, 给出了满足子系统共振、耦合强度到达USC 区间所需的电路元件参数, 其中所有参数取值皆在cQED 实验室的可行范围内. 再次, 在此基础上, 进一步研究了USC 的双比特模型, 并提出该系统可作为非相干中介, 实现两个Transmon 比特间的量子态转移(quantum-state transfer, QST), 且在考虑一定耗散和退相干的影响下, 通过求解Lindblad 方程验证了该QST 过程具有一定的抗噪性. 最后, 对研究结果进行了总结和展望.

1 模型与哈密顿量

图1 所示为单量子比特超导电路模型. 它由一个LC 谐振子(红色)通过电容器Cc(绿色)与CPB 系统(蓝色)耦合组成, 其中振荡电路(LC 谐振子)由电容器Cr与电感器Lr并联构成; CPB 包含了电容器CJ和约瑟夫森结EJ. 为了控制电路中的库珀对数目, 将电压源Vg通过门电容Cg与约瑟夫森结耦合. 此外,ΦJ、Φr和Φ1分别为描述CPB 系统、LC 谐振子和接地电容Cp的分支磁通量, 并得到系统的拉格朗日量为

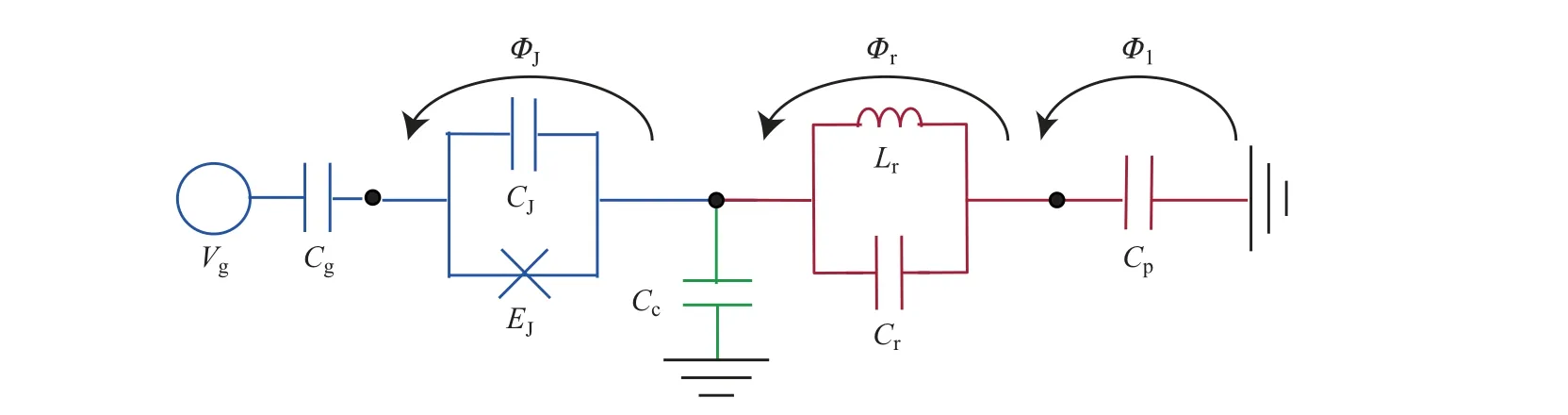
图1 LC 谐振子(红色)与单个CPB(蓝色)通过电容器Cc(绿色)耦合的单量子比特超导电路示意图Fig.1 Illustration for the one-qubit superconducting circuit where the LC resonator (red) coupled to the CPB (blue) through capacitor Cc (green)

式中,QJ和Qr分别表示CPB 系统与LC 谐振子的电荷量(QJ≡∂L1/∂˙ΦJ). 此外, 考虑CPB 系统的门电荷数ng= 0.5, 定义系统的有效约瑟夫森电容(～CJ)、谐振子电容(～Cr)、耦合电容(CJr)和门电容(CJg、Crg)分别为

本工作假定CPB 系统处于电荷区间, 且门电荷数ng= 0.5. 在这种情况下, CPB 系统低能级间的非谐性很高, 可以被有效近似为一个频率为ωq的二能级系统, 即电荷量子比特[3], 其中ωq=EJ仅依赖于约瑟夫森能量. 同时, CPB 系统的库珀对数算符可以表示为^nJ=(I+σx)/2, 其中I 是单位矩阵,σx为泡利矩阵. 在这种近似下, 式(9)的哈密顿量变为

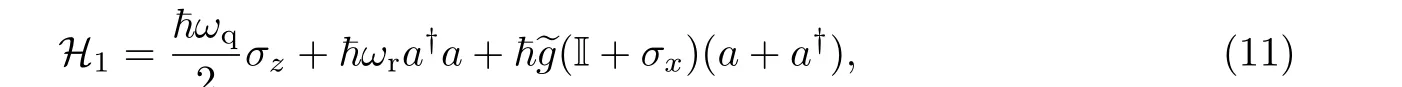
式中, ～g=g/2 为CPB 系统与LC 谐振子之间的有效耦合强度. 需注意, 当～g很小时, 耦合项I(a+a†)可以被绝热消除. 此时, CPB 和单模谐振子之间光与物质的相互作用由量子拉比模型描述, 即

然而, 随着耦合强度～g的增加, 耦合项I(a+a†)将改变系统的动力学. 如图2 所示: 当系统耦合强度～g/ωr∈[0,0.3]时, 系统处于微扰USC 区[27], 哈密顿量H1和HQRM的能谱高度重合; ～g/ωr∈[0.3,1]时, 系统处于非微扰USC 区间, 此时两种模型的能谱不再重叠, 哈密顿量H1和HQRM将描述不同的物理现象. 本工作将致力于探索光与物质的耦合强度上限, 并实现子系统相互作用的USC 以及DSC. 因此, 本工作用哈密顿量H1而非HQRM描述CPB 系统和单模谐振子之间的相互作用.

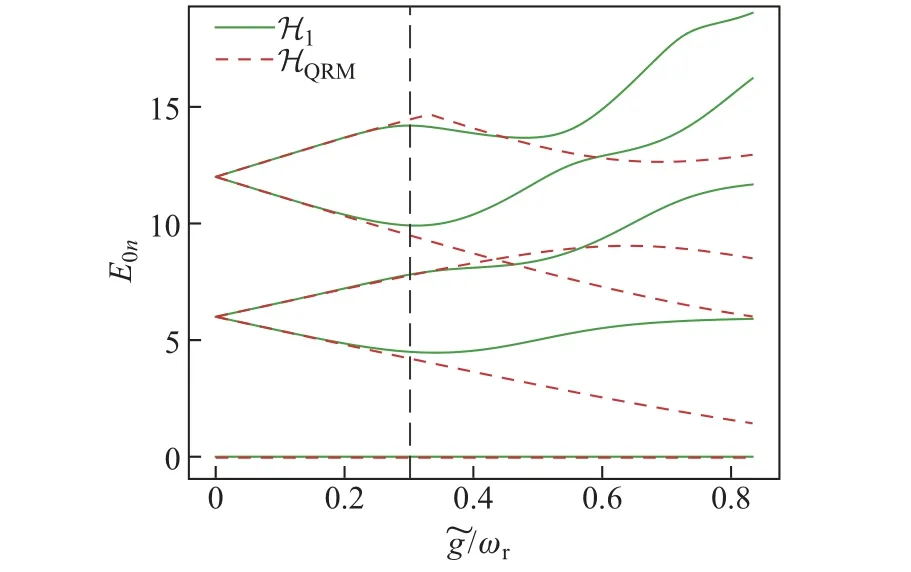
图2 哈密顿量H1 和HQRM 的能谱与耦合强度～g/ωr 的关系图Fig.2 Energy spectrum of Hamiltonian H1 and HQRM as a function of coupling strength ～g/ωr

1.1 耦合强度

为了进一步研究耦合强度～g与电路物理参数之间的依赖关系, 并描述子系统(CPB 和LC谐振子)之间的共振情况, 定义耦合比率R为

分析比值γ可知, 当Cg、Cp≫Cc、CJ时,γ近似为1. 此时, 式(14)中的耦合比率仅依赖于参数x, 即Rres≈x. 这意味着系统耦合比率将随谐振子阻抗～Zr的增长而持续增加[28].

综上所述, 在图1 所示的单量子比特超导电路中, 耦合强度不存在基本极限. 当选取合适的电路参数(EJ、～Zr)时, 系统的耦合强度可以到达USC 区间, 甚至是DSC 区间.

为进一步研究单量子比特超导电路中耦合比率R和电路元件取值的依赖关系, 并验证在上述计算中使用二能级近似的合理性, 本工作利用Python 语言的优化算法, 通过优化目标函数(objective function)来得到相应的优化数值解, 其中目标函数定义为

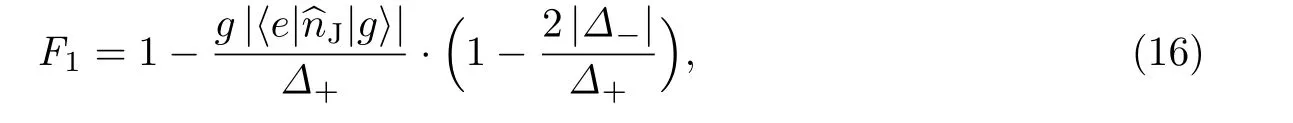
式中:ωq和〈e|^nJ|g〉是通过数值计算五能级CPB 系统获得的;|g〉和|e〉分别是CPB 系统的基态和第一激发态;Δ±=ωq±ωr. 该目标函数能在维持子系统共振的情况下, 使得R不断增长至最佳值. 同时在优化过程中对参数选取进行了限制, 以确保所得元件参数在目前cQED 实验室的可行范围内[29], 即电容C ∈[0.11,550]fF、电感L ∈[100,1000]nH、约瑟夫森结EJ∈2π[4,11]GHz.

基于上述优化程序可获得耦合比率R与比值EJ/EC的依赖关系, 如图3 所示, 其中蓝色散点是由优化算法得到的数值结果, 而橘色散点是通过解析式(13)所得. 在计算过程中, 固定了电路中所有的电容器与电感器取值, 仅改变了约瑟夫森能量EJ. 由图3 可见, 解析解和数值解之间具有高度一致性, 证实了本工作对CPB 系统施加二能级近似的合理性, 以及式(13)中耦合比值定义式的准确性. 此外, 由图3 还发现, 当CPB 系统向电荷区间趋近时, 耦合强度不断增加, 直至达到DSC 区间(R=2.92).

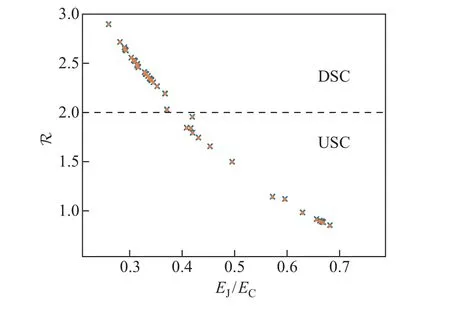
图3 耦合比值R 与EJ/EC 的关系Fig.3 Relationship of coupling ratio R as a function of EJ/EC

图4 在不同谐振子阻抗～Zr 下, 耦合比值R 与EJ/ħ 的关系Fig.4 Relationship of coupling ratio R as a function of EJ/ħ for different oscillator impedance

1.2 优化参数

通过最小化目标函数F1, 本工作获得了实现单量子比特超导电路中, 子系统USC 所需的电路元件参数, 并且在优化过程中, 始终将元件的取值约束在实验可行范围内[29,32]. 表1 总结了电路元件取值, 以及相应的哈密顿量中的物理参数和比值, 其中CPB 系统与谐振子满足共振条件ωr=ωq=2π×8.53 GHz, 且二者之间的耦合强度达到USC 区间. 需注意, 为了实现较大的耦合强度, 需要构造一个高阻抗谐振子, 但这会导致谐振子的电感非常大. 然而, 基于目前的超导技术, 通过构建一个约瑟夫森结链, 其有效电感可以达到L≤2.5 μH[32]. 这为本工作参数选取的合理性提供了理论支撑.

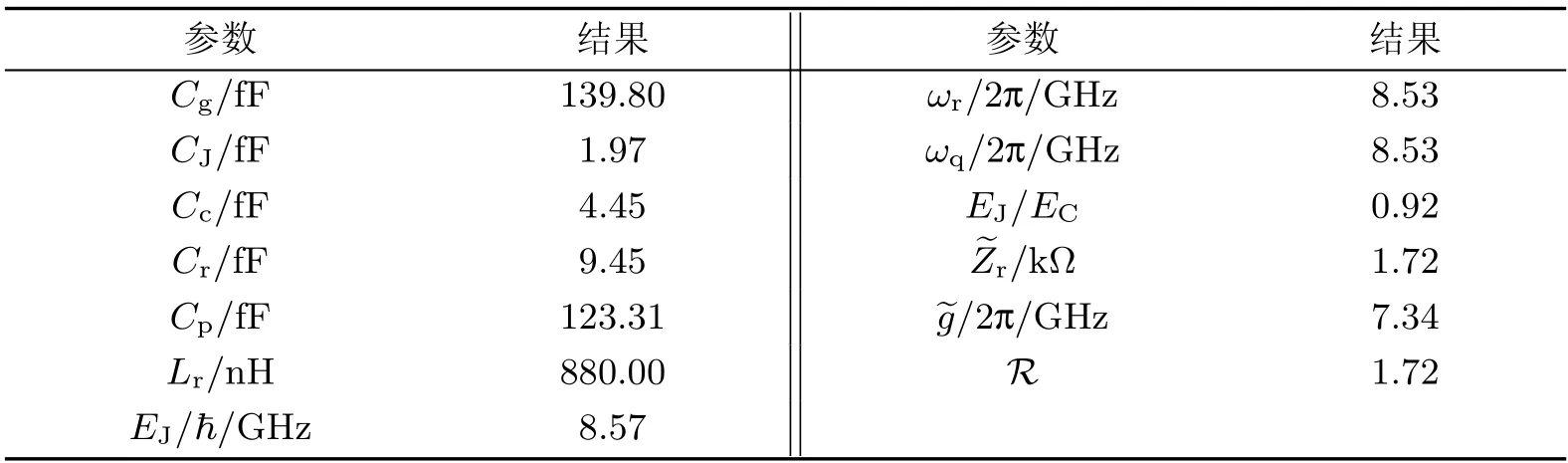
表1 单量子比特超导模型的电路参数以及相应的哈密顿量参数和比值Table 1 Circuit parameters and the Hamiltonian parameters/ratios of the one-qubit superconducting model

上述对于单量子比特超导电路模型的研究结果可以推广至如图5 所示(其中Φ0、Φr、ΦJ1和ΦJ2分别对应于通过电容器Cc0、LC 谐振子和2 个CPB 的磁通量)的双量子比特超导系统,其哈密顿量可以表示为

图5 LC 谐振子与2 个CPB 耦合的双量子比特超导电路示意图Fig.5 Schematic diagram of the two-qubit superconducting circuit where the LC resonator coupled to two CPB

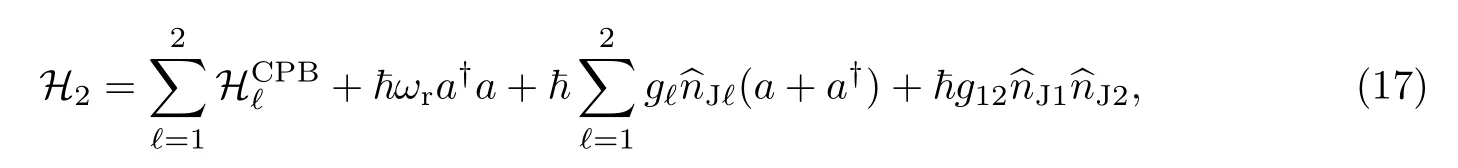
式中:gℓ是第ℓ个CPB 和LC 谐振子之间的耦合强度;g12是2 个CPB 之间的耦合强度. 本工作仅研究物质(CPB)与光(LC 谐振子)之间的耦合强度. 因此在探索双比特系统时, 对优化问题进行了限制, 以抑制量子比特之间的直接相互作用, 即考虑2 个比特之间的耦合强度

表2 双量子比特超导模型的电路参数以及相应的哈密顿量参数和比值Table 2 Circuit parameters and the Hamiltonian parameters/ratios of the two-qubit superconducting model

综上所述, 通过解析和数值计算, 本工作证明了在电荷量子比特与LC 谐振子耦合的电路中, 耦合强度不存在基本上限. 通过增大谐振子阻抗和减小约瑟夫森能量, 可以在子系统共振的情况下, 到达USC/DSC 区间.

2 量子态的转移

第1 节讨论了实现CPB 系统与LC 谐振子USC 和DSC 所需的物理条件. 第2 节将进一步分析图5 中双CPB 模型的能谱特性, 并将此构造块作为非相干中介(incoherent mediator)[33],以执行QST, 即将激发态从一个Transmon 系统, 通过非相干中介(双比特USC 模型)转移到另一个Transmon 系统上(见图6).

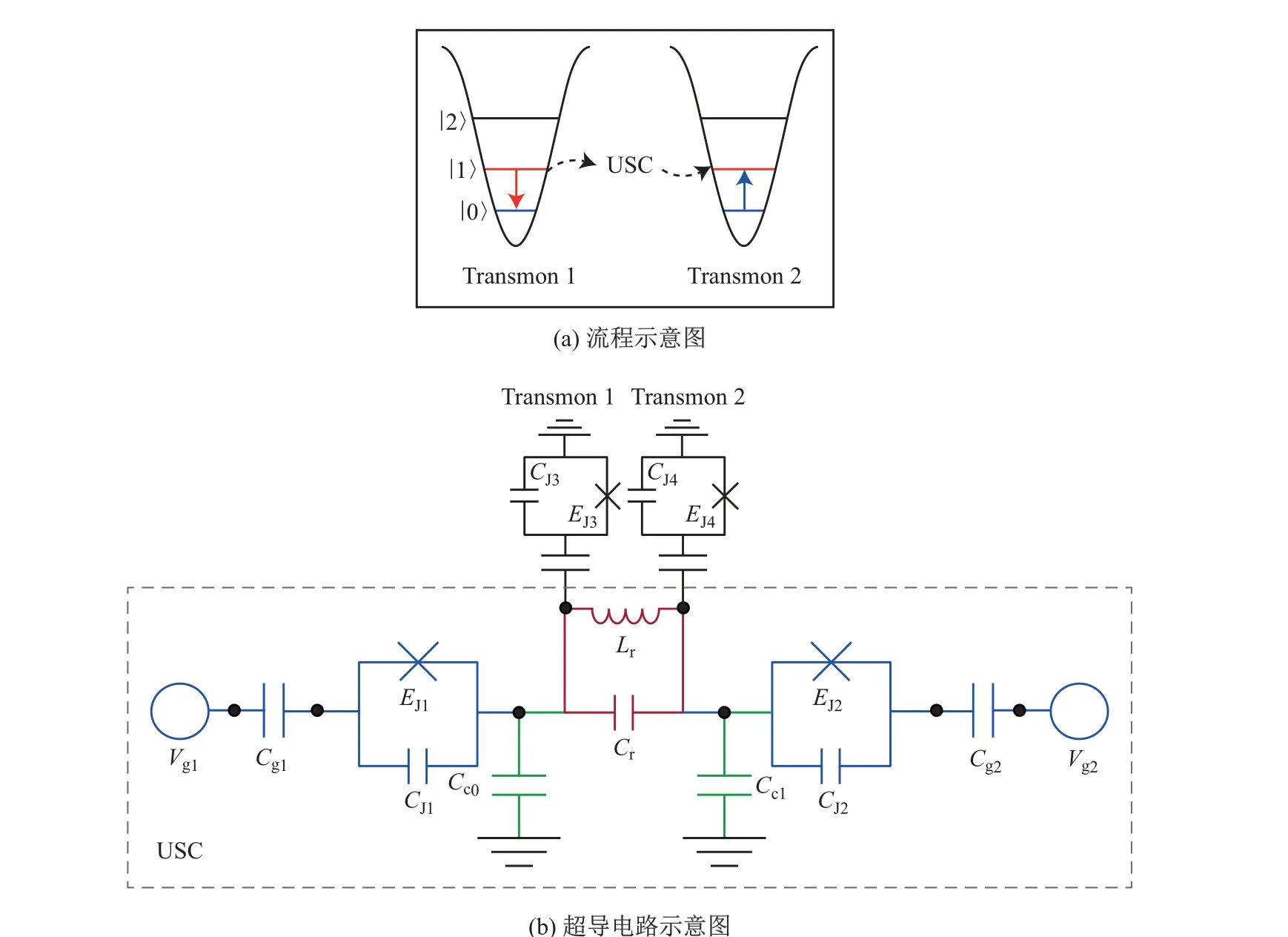
图6 实现QST 的示意图Fig.6 Illustration of the QST protocol

首先, 运用二能级近似, 将式(17)中的两个CPB 缩减为二能级系统, 得到中介系统的哈密顿量为

其次, 如图6 所示, 考虑两个Transmon 系统分别以耦合强度λ1和λ2与USC 中介通过电容器C2和C3耦合. 因此, QST 模型的总哈密顿量可以表示为

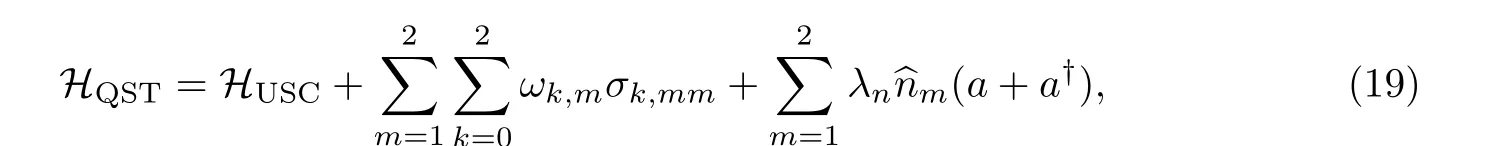
式中:ωk,m是第m个Transmon 系统的第k个能级的频率;σk,mm=|km〉〈km|和^nm分别是Transmon 系统的投影算符和库珀对数算符. 需注意, Transmon 系统的相对非谐性较低[34], 无法将其直接近似为一个二能级系统. 因此在哈密顿量HQST中, 会先考虑三能级Transmon 系统, 并假设系统的相对非谐性为αr,j= (ω12,m-ω01,m)/ω01,m=-0.096(ωαβ,m=ωβ,m-ωα,m).

最后, 本工作将对式(19)中的哈密顿量展开具体研究, 并分别分析在幺正演化(不考虑外部环境)和考虑外部损耗的情况下, 量子QST 协议的有效性.

2.1 幺正演化

首先, 假定QST 系统不受外部环境影响, 并将系统的演化过程视为严格的幺正演化. 在执行QST 协议时, 需要调节Transmon 系统的一阶跃迁能ω01,m, 使其与中介系统的禁戒跃迁能共振. 在此情况下, Transmon 系统的能量无法被中介吸收, 进而转移到另一个Transmon 系统上,实现了QST.分析式(19)可知,中介系统的禁戒跃迁能与耦和算符(a+a†)相关.因此,通过数值计算耦和算符的矩阵元素〈ψj|(a+a†)|ψk〉, 可得系统的禁戒跃迁信息, 其中|ψj〉是中介哈密顿量在缀饰态下的本征态. 通过计算发现, 当～gℓ/ωr=0.3 时, 矩阵元素〈ψ1|(a+a†)|ψ3〉=0.这意味着USC 系统在|ψ3〉 →|ψ1〉之间禁戒跃迁, 可得禁戒跃迁能为Δ13. 当系统处于非微扰USC 区(～gℓ/ωr=0.5)时, 系统|ψ4〉→|ψ1〉之间禁戒跃迁, 其禁戒跃迁能为Δ14.

基于上述两个在不同耦合强度下的USC 系统禁戒跃迁能级, 对QST 过程展开具体的数值计算. 将QST 系统初始化为量子态|0〉|ψ0〉|1〉 ∈HTransmon1⊗HUSC⊗HTransmon2, 并分别在耦合比率为～gℓ/ωr= 0.3 和0.5 时, 数值计算Transmon 系统的动力学演化过程. 如图7 所示, 当CPB 频率与禁戒跃迁能共振时, 量子态|0〉|ψ0〉|1〉和|1〉|ψ0〉|0〉之间的布居数反转, 验证了本工作所提出的QST 协议的可行性. 此外, 随着CPB 系统与LC 谐振子耦合强度～g的增大, Transmon 系统量子态反转所需的时间也同样增加, 即当～g= 0.3ωr时, 量子态反转需要t= 17.75 ns; 而当～g= 0.5ωr时,t= 245.31 ns. 与此同时还发现, 布居数大多处于Transmons 的两个最低量子态(|0〉、|1〉), 而第二激发态并没有对系统动力学造成影响. 因此, 在接下来的讨论中, 仅考虑二能级Transmon 系统, 式(19)中的哈密顿量可以改写为

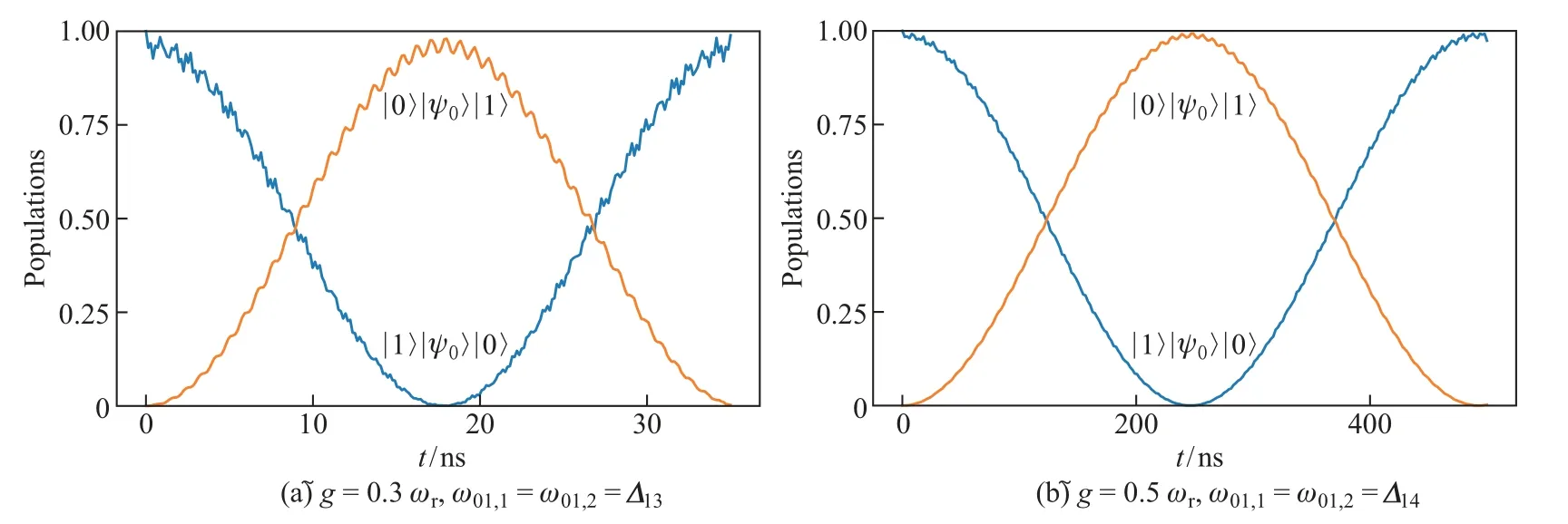
图7 量子态|1〉|ψ0〉|0〉和|0〉|ψ0〉|1〉的布居数(ωq,1 =ωq,2 =ωr =2π×6 GHz)Fig.7 Populations between the state |1〉|ψ0〉|0〉 and the state |0〉|ψ0〉|1〉 (ωq,1 =ωq,2 =ωr =2π×6 GHz)

2.2 系统损耗的影响

实际上, 量子系统并不完全孤立. 一方面, 需要利用与外部环境的耦合来控制量子系统;另一方面, 量子系统的某些自由度会与环境发生不可控的相互作用. 因此, 必须考虑QST 系统为开放量子系统, 并与一个热库弱耦合, 进而研究在损耗机制下QST 协议的鲁棒性. 需注意,当中介系统的耦合强度达到USC/DSC 区间时, 系统的耗散动力学很大程度上取决于子系统之间的相互作用, 因此, 早期量子光学中使用的标准主方程形式不再有效[35]. 在这种情况下,本工作遵循规范方法, 即在计算系统和环境相互作用时, 将USC 中介的哈密顿量对角化. 此时, 系统的衰减率取决于系统的跃迁能, 并且耦合算符σz在缀饰态中不再是对角化形式. 这意味着去极化噪声在引起退相位的同时, 会造成能量弛豫.

上述耗散物理现象都可以由主方程法描述, 它是研究开放量子系统的常用方法. 在推导主方程的过程中, 需要运用Markov 近似和Born 近似, 即考虑量子系统在t+dt时的量子态仅依赖于t时刻的量子态, 且量子系统不会影响环境的状态. 基于这两个近似, 可得Lindblad 主方程[35-37]为

式中,ωT=kBT/ħ 为热频率.

在上述计算过程中, 仅考虑了USC 中介的子系统(LC 谐振子、CPB)能量损失是由具有欧姆频谱密度的热库引起的[36], 而系统的量子相干性损失主要是由电荷噪声引起的[38].

因此, 基于式(21)中的QST 系统主方程, 在考虑损耗的情况下, 对QST 过程进行数值计算. 将系统初始化为量子态ρ1=|1〉〈1|⊗ρTh⊗|0〉〈0|. 这里中介系统的初态为热状态(thermal

图8 描述了当耦合强度～gℓ/ωr= 0.3 和0.5 时, Transmon 比特在损耗情况下的量子态布居数变化. 结果发现: 在t= 17.75 和245.31 ns 时, 量子态ρ1和量子态ρ2(ρ2=|0〉〈0|⊗ρTh⊗|1〉〈1|)之间的布居数反转; 当CPB 与LC 谐振子耦合强度较小时, 即～g= 0.3ωr时, 由于发生布居数反转所需的时间较短, 噪声并没有对Transmon 系统间的QST 造成太大影响.

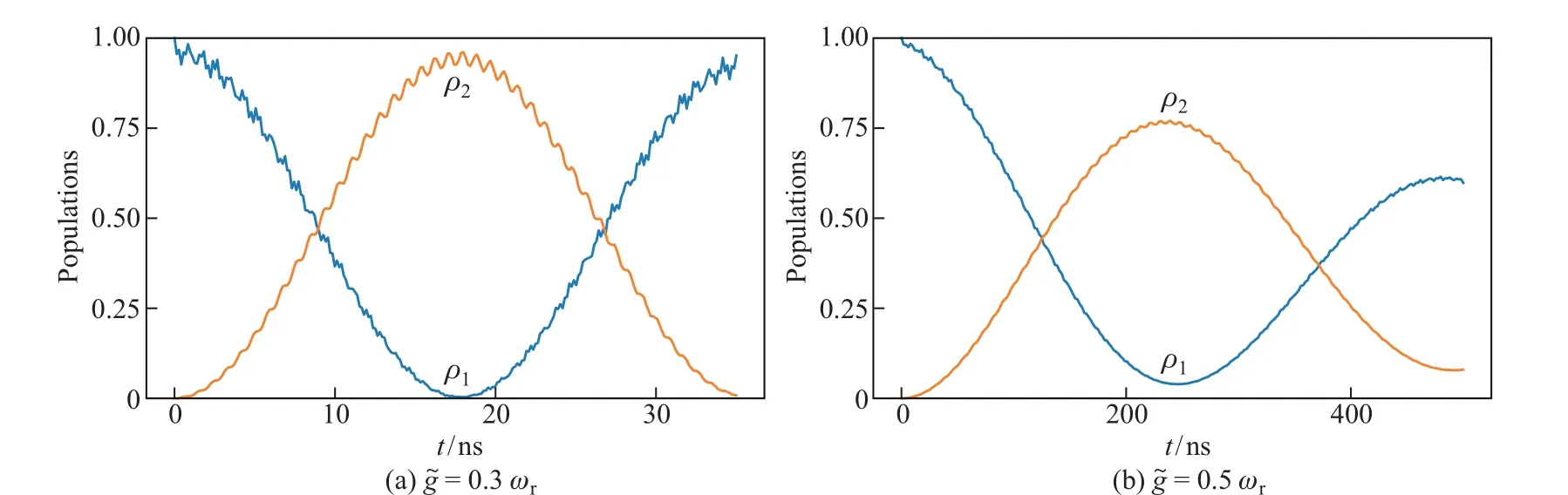
图8 在考虑系统损耗下, 量子态ρ1 =|1〉〈1|⊗ρTh ⊗|0〉〈0|和ρ2 =|0〉〈0|⊗ρTh ⊗|1〉〈1|之间的布居数(ωq,1(2) =ωr =2π×6 GHz, λ1(2) =0.02 ωr)Fig.8 Populations between the state ρ1 =|1〉〈1|⊗ρTh⊗|0〉〈0|and the state ρ2 =|0〉〈0|⊗ρTh⊗|1〉〈1|(ωq,1(2) =ωr =2π×6 GHz, λ1(2) =0.02 ωr) by considering dissipative system

为了进一步研究QST 协议的有效性, 本工作计算了QST 过程的保真度, 即FQST=tr(ρ(t)ρ2), 其中ρ(t)是式(21)中的主方程密度矩阵解. 如图9 所示: 当～g/ωr= 0.3 时, 系统的最大保真度为FQST= 0.980 3; 当～g/ωr= 0.5 时, 最大保真度为FQST= 0.878 3, 验证了本工作的推论.

图9 量子态ρ2 与ρ(t)之间的QST 过程保真度Fig.9 Fidelity of the QST process between the state ρ2 and the state ρ(t)

3 结束语

本工作基于CPB 系统与LC 谐振子耦合的超导电路模型研究了光与物质的相互作用. 结果表明, 通过减小约瑟夫森能量和增大谐振子阻抗, 耦合强度可以不断增加, 并且能够在子系统共振的同时, 到达USC/DSC 区间. 通过数值优化目标函数, 给出了在单量子比特系统与双量子比特系统中, 实现光与物质USC 所需的电路元件参数. 在此基础上, 利用所得的双量子比特系统作为非相干中介, 在考虑外部损耗的情况下, 实现了两个Transmon 比特间的QST,并验证了本方案在开放量子系统中具有一定的抗噪声能力. 本工作有望在多比特超导量子系统中实现USC, 并对多量子比特的制备、转移和抗噪声设计提供理论基础, 也为在光与物质USC 的超导量子系统中实现量子调控、模拟和量子信息处理提供了可选方案.