面向遥感图像的小样本目标检测改进算法研究

李成范 赵俊娟

( 1. 东华理工大学江西省数字国土重点实验室, 江西南昌 330013;2. 上海大学计算机工程与科学学院, 上海 200444)

随着星载传感器和小卫星技术的不断发展, 遥感技术已成为地球资源调查和生态环境监测的重要手段, 应用领域也越来越广泛[1-2]. 遥感图像中目标数量众多, 种类繁杂, 普遍存在小样本显著以及部分目标样本采集困难等现象. 如对于偏远地区或一些人类不易到达的地区, 不同类型的目标样本数量稀少、分布不均衡且目标尺度大小变化不一, 导致目标的可提取特征弱化. 早期的遥感图像目标检测主要是通过基于目视和像元解译实现, 目前已成为有效的遥感图像分析辅助手段[3]. 随后出现的面向对象的方法能够充分利用像元光谱和地物的空间与形状、纹理等特征, 尽管目标检测效果较好, 但是在对象分割过程中如何设定合理的分割窗口和分类特征则成为制约高精度应用的难点[4].

随着遥感数据量的激增, 传统的遥感图像分析方法已不能适应高精度遥感应用的需要,而新出现的一些遥感目标检测方法, 如神经网络、专家系统、支持向量机(support vector machine, SVM)等, 行业应用明显, 通常仅在某一领域中取得较好的效果, 普适性较差[5]. 深度神经网络是一种基于人工智能的分类算法, 该算法通过计算机来模拟人类学习过程, 使目标检测结果更趋于合理化和自动化, 具有较好的容错能力和强大的自适应性, 有效克服了传统遥感目标检测方法造成的模糊性和不确定性.K近邻(K-nearest neighbor, KNN)回归算法是一种基于统计的非参数模式识别分类算法, 其应用领域已由最初的时间序列预测逐渐扩展到多个领域的预测, 如文本分类预测、灾害监测、年平均降雨量预报等[6-8]. 然而, KNN 在学习过程中需要不断地存储已知的训练数据, 占用内存较大. VGG-16 模型包含卷积层、全连接层、池化层, 网络结构参数较少, 能够更加有效地学习到复杂的图像级特征[9-10]. 得益于强大的特征表示能力, 目前深度神经网络已经得到了深入关注和广泛应用[11-13].

小样本学习是从每类单个或少量样本中学习特定任务的信息. 早期尝试小样本问题的算法是基于稀疏表示的方法[14]. 随着基于贝叶斯理论的表示方法的提出, 先验知识被更好地引入和利用[15-16]. 但是, 这些早期的传统方法往往是针对具体问题设计的, 其模型通用性较差.随着深度学习的兴起, 小样本学习有了更广阔的研究空间, 吸引了越来越多研究人员的关注,且所提出的模型具有更好的通用性. 例如, 早期出现的孪生网络、匹配网络、原型网络、图神经网络、协方差度量网络等度量学习方法[17-20]能够有效地提升小样本学习的性能. 目前, 基于度量学习的小样本分类方法大多为上述网络的改进, 通过考虑样本局部信息, 尽可能地捕捉类内相似、差异和类间差异, 从而提高分类的准确性; 基于长短时记忆神经网络(long short-term memory network, LSTM)的元学习器模型、模型无关元学习、Reptile 元学习优化算法、基于元学习的训练网络、meta-transfer 算法等的深度学习模型, 通过梯度的反向传播解决了在训练样本不足的情况下梯度学习收敛问题[21-23]. 尽管基于深度学习的小样本分类算法取得了一些进展, 但是仍然存在一些问题, 如非常依赖于源域且很难应用到与源域差别较大的情形中[24], 小样本目标检测中源域有大量样本而目标域仅有少量标注的样本[25], 采用少量卷积层作为特征提取大多不能有效提取图像的特征[26], 算法通用性较弱, 难以适用于存在少量样本且缺少大量无标注样本问题等.

传统的小样本目标检测方法普遍存在目标类型判别不稳定、特征提取能力较弱, 而部分新兴算法网络复杂度较高, 迁移学习能力较弱等问题. 纵观众多基于遥感图像的小样本分类算法, 目前以深度学习算法最为有效. 其中, 深度神经网络具有强大的复杂网络模型学习能力, 可以满足高精度的遥感图像小样本分类需求. 本工作提出了通过利用KNN回归构建局部邻域, 同时分别利用卷积神经网络(convolutional neural network, CNN)卷积层和最大池化层进行特征提取与特征聚合, 提高局部特征的鲁棒性; 最后, 利用全连接层与缩放指数型线性单元(scaled expected linear unit, SELU)激活函数计算不同类别小样本目标的概率并进行分类. 实验结果表明, 基于改进的CNN 算法能够更有效地融合局部特征, 提高遥感图像小样本目标识别与检测精度, 保持信息的非局部扩散.

1 算法原理

1.1 VGG16 模型和KNN 回归模型

VGG16 网络通过堆叠多个小尺度的卷积核和引入多个非线性层操作, 一定程度上提高了网络学习复杂特征的能力, 减小了模型的优化参数, 模型泛化能力更强.

假定n维空间中任一个样本的最近邻均可用欧氏距离定义, 则对于任一样本x的特征向量x=(x1,x2,··· ,xi), 那么2 个样本xm和xn在2 维空间中的距离可以定义为

式中:xi为样本x的第i个特征值. 对于待分类样本xm而言,x1,x2,··· ,xk为训练集中与xm距离最近的k个最近邻样本.

1.2 改进CNN 算法

假设深度网络表示的函数为fθ, 每个样本及其对应标签记为(xi,yi),Sj表示为支撑集中类别为j的样本集合, 则每个类的原型为

给定一个距离度量d, 原型网络基于查询样本到其他原型之间距离和SELU 激活函数归一化而产生的类别的分布为

对于每幅图像, 经过CNN 提取特征后, 利用卷积层、池化层和激活函数层进一步进行特征嵌入, 生成一个局部特征, 进而得到融合局部特征的图像嵌入表示. 对每类支撑集中的样本的特征嵌入进行平均, 得到每类的原型. 此时查询样本取每类原型概率值的最大值作为查询样本属于该类别的概率. 但是在考虑局部特征时增加了网络复杂度, 在小样本条件下, 引入Triplet Loss 代价函数来增强特征的表达能力:

图1 为本工作提出的改进CNN 算法模型示意图, 图中卷积核大小为3×3, 池化层的步长为2. 该模型包含一个VGG16 结构、13 个卷积层、5 个池化层和3 个全连接层以及嵌入CNN中的KNN 结构.

图1 改进的CNN 模型结构Fig.1 Improved CNN model structure

在该模型中, 首先输入原始数据, 经过VGG-16 处理形成n×3 维的张量; 构建每个点的局部邻域得到3 个n×k维的特征图; 经过卷积操作形成64 个n×k维的特征图; 对于第3 次池化操作后生成一个1 024×1 维的特征向量, 通过全连接层进行分类; 最后采用SELU 激活函数将全连接层的输出转化为相对应的概率. SELU 能使CNN 每一层的输出自动归一化到均值接近0. 方差接近1 的高斯分布, 训练效果更佳, CNN 模型鲁棒性更强. 这里, 各类别对应的概率表达式为

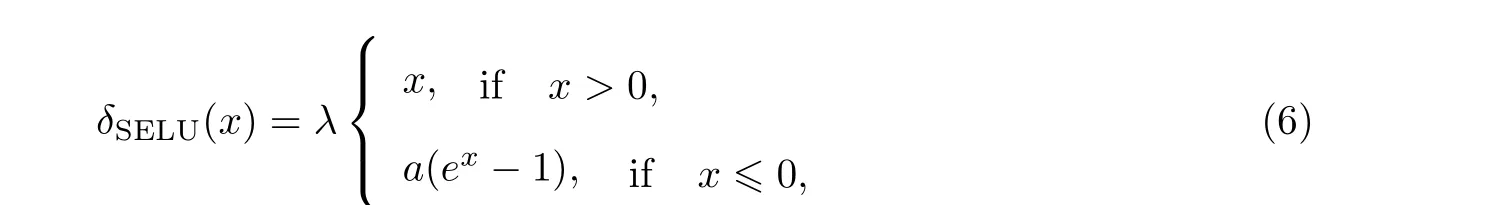
式中:λ为缩放因子,λ=1.05;α为常数,α=1.67.

2 实 验

2.1 数据集和预处理

本工作将采用超光谱成像(hyperspectral imager, HSI)仪高光谱遥感数据集验证所提算法的准确性. HSI 传感器搭载在中国首颗环境与减灾卫星(HJ-1A)上, 回归周期为4 d, 谱段范围为0.45～0.95 μm, 拥有115 个谱段数, 平均光谱分辨率为5 nm, 系统信噪比为50～100 dB. 本工作中获取的数据为HSI 的2 级产品. 本实验室拥有自建的HSI 高光谱数据集, 该数据集共包含6 类场景, 每类场景中都有300 幅500×500 像素的图像. 该数据集的选取标准之一就是同一地物类型内部之间差异大、不同地物类型之间相似度高, 更有利于测试算法的准有效性. 其中, 随机选取各类型地物目标的60%作为训练, 20%进行验证, 余下20%进行测试(下文中的全部试验结果都是基于ImageNet 数据集迁移学习而得到的).

在深度网络学习语义特征时, 由于缺少足够多的标注样本, 故往往会导致网络参数训练效果不理想. 在实验中, 首先在ImageNet 上预训练VGG16 的网络参数, 将图像级分类网络转换为像素级特征预测网络; 随后在KNN 回归构建局部邻域的基础上, 分别利用CNN 卷积层和最大池化层进行特征提取与特征聚合; 最后将通过训练好的网络参数迁移提取HSI 数据集中潜在的深层结构信息, 得到表征HSI 数据集空间分布的21 个特征结果(见图2).

图2 HSI 图像空间分布Fig.2 Spatial distribution in HSI image

图2 为HSI 图像空间分布图. 在图2 中, 不同的特征图分别对应神经网络预测层的若干神经元, 不同的目标在每个神经元能够产生相应的反应. 通过融合局部特征的深度神经网络能够更好地识别和检测出HSI 数据集中局部细节信息.

本实验采用自适应矩估计(adaptive moment estimation, Adam)优化器优化CNN 模型. 设置初始学习率为0.001 5, 动量设置为0.9, 批量规模(batch size)设置为32, 丢弃率(dropout)设置为0.5, 网络训练初始权重w初始化为高斯分布的随机数, 初始偏差b设置为0. 训练中通过对图像的曝光量、色调和饱和度等不断进行调整, 以此提高模型的泛化能力.

本实验是在Anaconda 平台上通过Python 3.7 实现,编程环境为Cuda-toolkit 8.0,深度学习框架为Tensorflow2.0, 所有的实验均在Intel Xeon E5-2620 v4 CPU,Nvidia Quadro M4000 GPU(内存为8 GB)的Linux Ubuntu 系统上完成的.

2.2 目标检测评价指标

在实验中, 本工作主要采用总体精度(overall accuracy, OA)和Kappa 系数等指标对提出的测算法进行性能评估. 此外, 为了得到较准确的评估结果, 本实验均采用50 次实验的平均分类结果进行统计.

本实验总精度的计算公式为

式中:N为所有真实参考的像元总数;xii为混淆矩阵对角线;r为不同的目标类型.

Kappa 系数的计算公式为

式中:i+为矩阵行元素; +i为矩阵列元素.

通常来说, Kappa 系数的计算结果范围为[-1, 1], 一致性程度按照Kappa 系数范围均匀地划分为轻微、一般、中度、大量和近似完全这5 个等级. Kappa 系数数值分布和一致性之间的关系如表1 所示.

表1 Kappa 数值分布与一致性的关系Table 1 Relationship between the Kappa numerical distribution and consistency

3 结果分析

3.1 不同K 值和样本数量变化

在利用KNN 回归构建局部邻域的过程中, 不同近邻点K值条件下的局部结构信息并不完全相同. 表2 展示了K值与改进算法精度的关系.

表2 K 值与改进CNN 算法精度的关系Table 2 Relationship between the K value and accuracy of the improved CNN approach

从表2 中可以看出, 随着邻近点K值的增大, 本算法的总体分类精度不断提高, 且增大的幅度随着K值的增大逐渐减小, 表明在构建局部邻域时局部邻域内必须包含一定数量的特征,避免局部特征数量较少对识别分类结果产生的影响. 但是,K值的增大在一定程度上会引起构建的局部邻域增大, 训练耗时增加.

图3 展示了本算法与CNN、CRNN、LSTM 等常用算法之间分类精度与训练样本数量的关系.

图3 不同算法分类精度与训练样本数量的关系Fig.3 Relationship between different approaches and training samples

从图3 中可以看出, 在小样本条件下, 尤其是在训练样本数量为0～200 时, 本算法的分类精度要明显的优于其他3 种方法, 且随着训练样本数量的增加, 不同算法的分类精度也呈现逐渐增高的趋势. 本算法在训练样本数量为200 时达到了最优的分类精度(约为97%); LSTM 算法变化趋势与本算法一致, 但是其总体分类精度要低于本算法; CNN 和CRNN 算法达到最高分类精度所需要的训练样本数量要多于LSTM 算法和本算法. 当样本数量达到500 时, 不同算法的分类精度逐渐趋于稳定. 此后, 随着样本量的持续增加, 不同方法的分类精度并未出现明显增高, 这在一定程度上体现出本算法在小样本条件下的适用性和准确性.

3.2 算法精度和时间复杂度

表3 分别展示了CNN、CRNN、LSTM 和本算法的训练情况与测试精度.

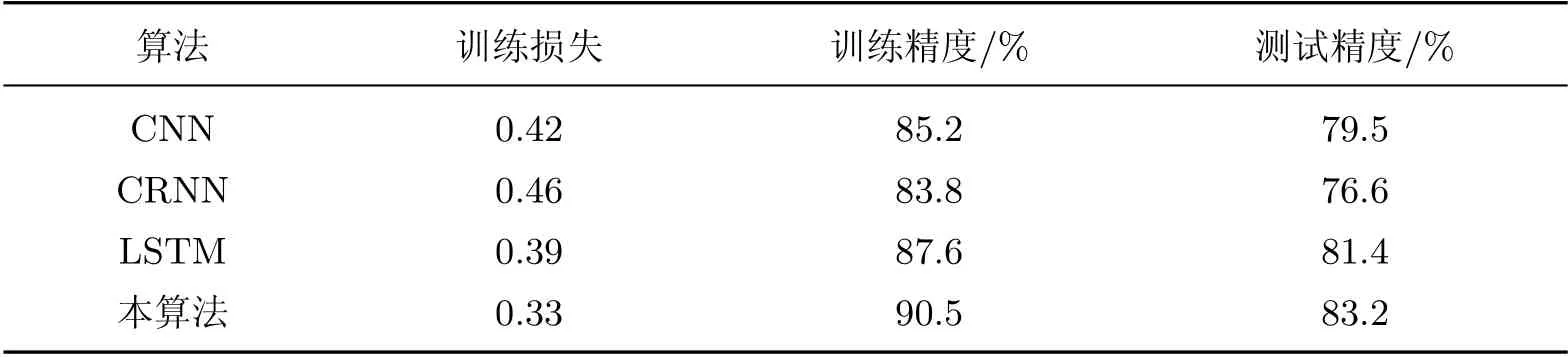
表3 训练情况和测试精度Table 3 Training and testing accuracy

从表3 中看出, 本算法在训练集上的精度达到90.5%, 损失为0.33, 都要优于传统的CNN、CRNN 和LSTM 方法. 相应地, 在测试集上, 本算法的精度达到83.2%, 也优于上述3种方法的测试精度, 表明本算法能够有效地从HSI 图像中检测出小样本目标.

图4 和表4 分别展示了本算法和CNN、CRNN、LSTM 算法在相同HSI 数据集中的小样本目标检测结果.

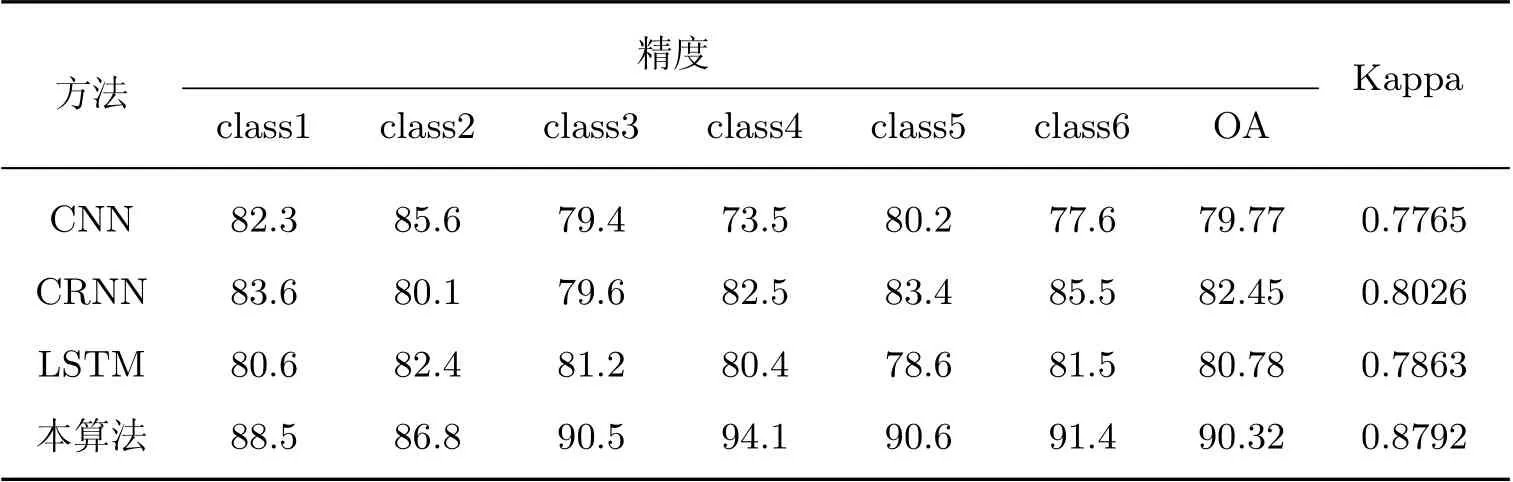
表4 不同方法分类对比结果Table 4 Comparison results of different methods

从图4 中看出, 由于本算法能够通过融合局部特征更有效地获取图像的全局特征, 故在一定程度上加强了小样本目标的边界定位特征, 使其在分辨率较低的遥感图像应用中的表现更为突出.

图4 HSI 遥感图像检测结果Fig.4 Detection results of HSI remote sensing images

从表4 可以发现, 在整体检测类型方面, 本算法在HSI 数据集上的分类精度达到90.32%,Kappa 系数达到0.879 2. 与其他3 种算法相比, 本算法的检测精度优势明显, 这也在图4 中得到了验证, 本算法的检测图像目视效果最好. 另外, 在单一检测类型方面, 本算法获取的单类别目标信息的精度普遍优于其他算法的效果. 其中, 纵观不同类型检测信息, class4 和class5的检测结果混淆程度最大, 而其他类别混淆程度相对较小. 据分析, 这主要是由于class4 和class5 的地物目标光谱特征较为接近, 在检测过程中极易引起错误识别, 这也与图4(b)和(c)的检测结果相一致. 尽管class4 和class5 的混淆较为严重, 但是本算法得益于局部特征融合, 在完成高检测精度的同时仍能确保较好的空间一致性.

表5 展示了不同算法在相同HSI 数据集上的平均运行时间对比. 为了获得公平稳定的时间对比, 实验中将在不同样本数量情况下分别统计50 次运行的时间均值作为该算法的运算时间.

表5 不同算法平均运行时间对比Table 5 Comparison of operation time of different approaches

在表5 中, 与传统的CNN、CRNN 和LSTM 算法相比, 本算法需要较多的运行时间. 据分析, 这主要是由于本算法中的最优邻域窗口半径较小, 在小样本条件下大量重复计算的劣势逐渐凸显出来, 计算复杂度急剧增大. 尤其是当各类样本数量低于400 时, 这种现象更加明显.尽管本算法具有较高的时间复杂度, 但是随着样本量的增加, 运行时间并未出现急剧性增加,在通常情况下这些差距被认为在可接受范围内.

4 结束语

针对遥感图像目标检测研究中面临的小样本以及每类地物目标样本随机分布等问题, 本工作提出了一种面向遥感图像的小样本目标检测改进算法. 通过KNN 回归和CNN 网络卷积层提取了特征构建局部邻域, 进而聚合所有局部特征来表示全局特征, 从而提高小样本目标检测精度. 本算法在HSI 高光谱遥感数据集上得到验证. 实验结果表明, 与传统的CNN、CRNN、LSTM 算法相比, 本算法在小样本条件下构建局部邻域时通过包含一定数量的局部特征, 显著提高了目标的检测精度, 同时又保持整体信息的非局部扩散. 尽管如此, 本算法在处理极少样本情况下的数据时, 目标检测耗时较长, 后续的改进可从如下2 个方面着手:①对模型参数和K值的选择进行优化, 构建合理的参数选择机制; ②基于本算法模型层数相对较浅难以提取更深层次的特征, 制定与模型计算量和计算复杂度相适应的模型层数.