Λc(2880)+ 2D 波激发态的强衰变

李 阳, 张爱林

(上海大学理学院, 上海 200444)

目前对于重味重子内部是否存在双夸克(diquark)[4,6,8], 即2 个轻夸克结合形成1 个双夸克结构, 还没有确切的证据. 对激发态Λc粲味重子强衰变的研究, 有助于提供更多关于重味重子内部结构的有用数据, 并为确定双夸克结构是否存在提供更多信息.

1 Λc 粲味重子的标记方式

重子属于三体系统, 为了方便研究, 本工作利用ρ模和λ模描写重子的坐标, 即2 个轻夸克间的相对位置用ρ坐标表示, 2 个轻夸克系统和重夸克之间的相对位置用λ坐标表示(见图1).ρ坐标和λ坐标的定义参考文献[9-10].

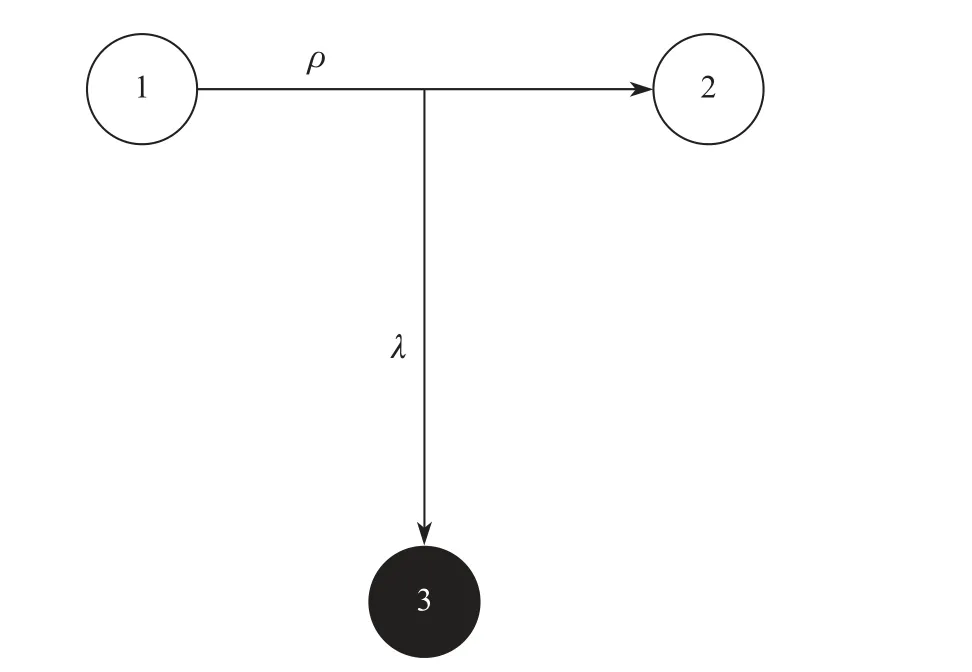
图1 重子内部坐标构造Fig.1 Inner coordinates of baryons

本工作用lρ表示2 个轻夸克间的相对轨道角动量,lλ表示2 个轻夸克系统与重夸克之间的相对轨道角动量. 夸克1 和夸克2 的总自旋为Sρ=s1+s2; 总轨道角动量为L=lρ+lλ、JL=L+Sρ; 总角动量为J=JL+s3.

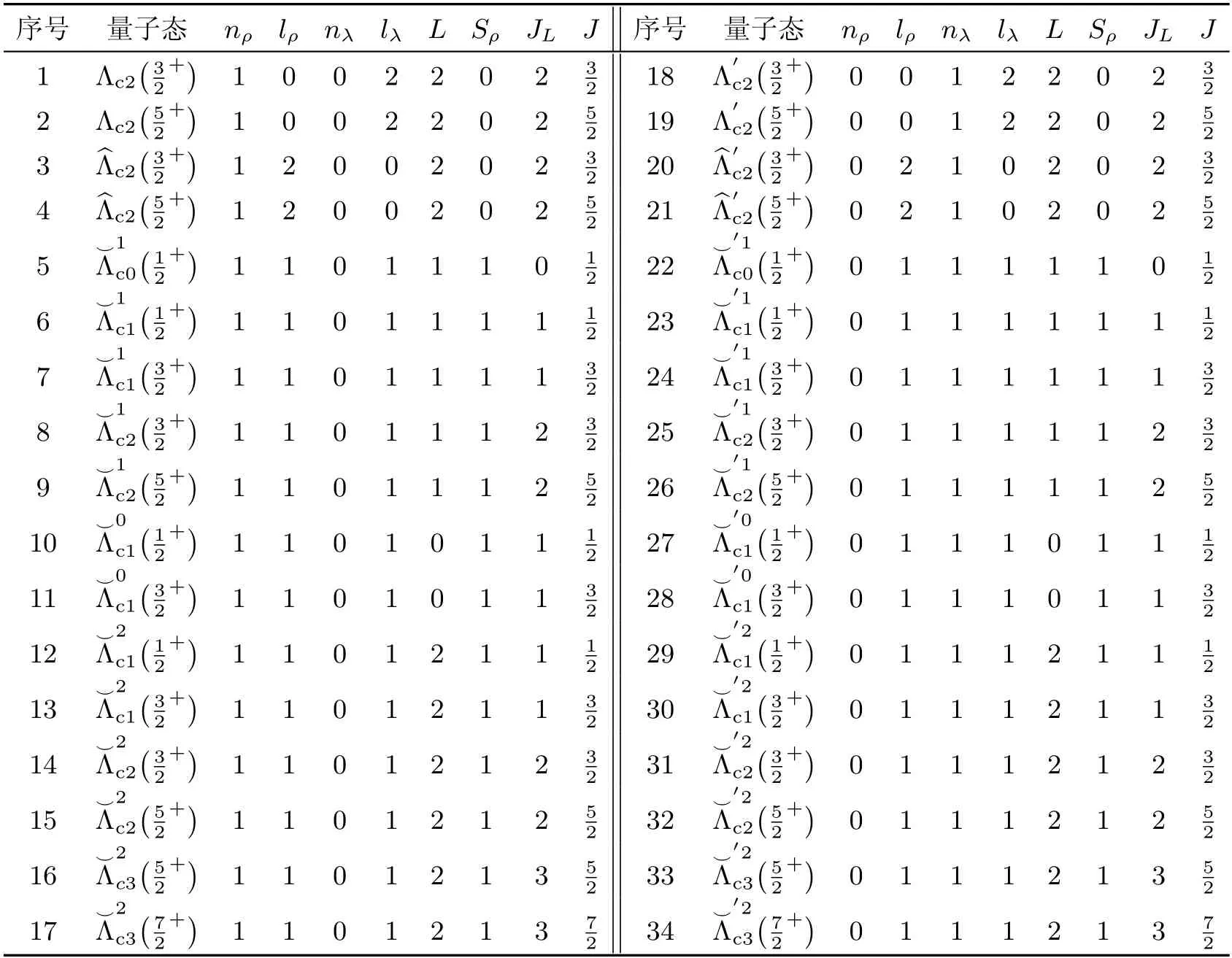
表1 2D 激发Λc 的量子数和符号标记Table 1 Notations and quantum numbers for 2D-wave Λc

表2 末态重子的量子数Table 2 Quantum numbers of baryons in the final states

2 重子在3P0 模型中的衰变

2.1 3P0 模型简介

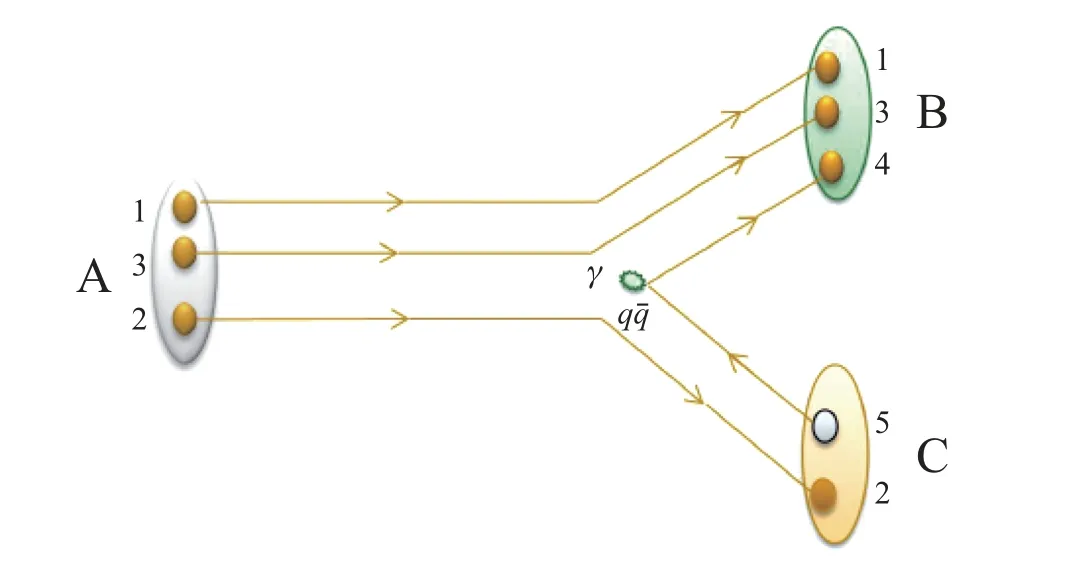
图2 3P0 模型框架下重子的衰变过程A→B+CFig.2 Baryons decay process A→B+C in the 3P0 model

3P0模型主要用来研究OZI(Okubo-Zweig-Iizuka)规则下的强子强衰变. 在3P0模型框架下, 真空中产生的夸克对的量子数为JPC= 0++. 按照真空扰动理论的要求, 新产生的夸克对的颜色和味道必须是单态, 具有正的宇称, 且总角动量J= 0. 在标准模型下, 夸克对的宇称P= (-1)L+1, 电荷共轭C= (-1)L+S. 当真空扰动条件全部满足时, 真空中产生的夸克对的量子态为2S+1LJ=3P0. 这就是3P0模型名称的由来.

除3P0模型外, 目前已经有包括量子色动力学(quantum chromodynamics, QCD)求和规则和手征夸克模型在内的多种模型被用来研究重味重子的强衰变[5,19-23].

2.2 3P0 模型框架下衰变宽度的计算

按照3P0模型理论, 重子的强衰变通过夸克重组的方式发生, 即真空中产生的正反夸克对和初始重子中的3 个夸克重新组合成末态重子和介子. 粲味重子的强衰变有3 种夸克重组方式[11], 即

式中:mA和JA分别为重子A 的质量和总角动量量子数;MJ为磁量子数;MMJAMJBMJC为螺旋度振幅(衰变振幅). 在衰变宽度计算过程中, 选取初态重子A 的质心系作为参照系,p是在此参照系中末态重子B 的动量, 具体表达式为

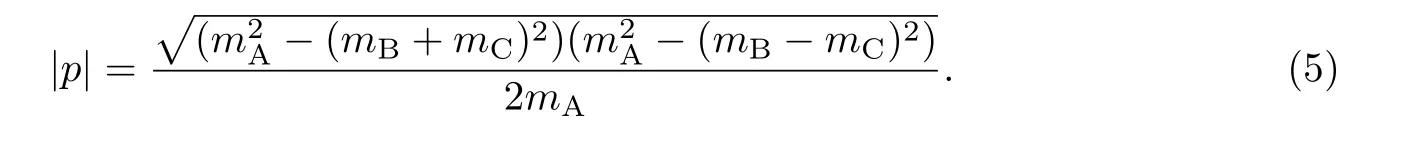
在初态重子A 的质心参照系下,pA=0,pB=-pC=p.

当激发态粲味重子衰变成一个粲味重子和一个轻介子, 即式(1)和(2)表示的重组过程时,以式(2)表示的夸克重组方式为例, 总衰变振幅[11,18,24]为

在3P0模型中, 采用简谐振子波(simple harmonic oscillator, SHO)函数作为强子的空间波函数. 重子由3 个夸克构成, 属于三体系统, 为了计算方便引入Jacobi 坐标. 在Jacobi 坐标下, 重子空间波函数为ρ分量和λ分量的乘积[18,25-27], 即

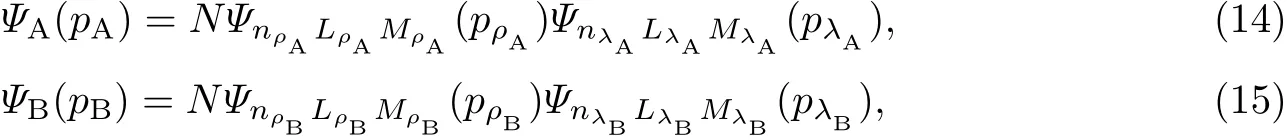
式中:n、L、ML分别为径向量子数、轨道角动量量子数和磁量子数;LL+1/2n(p2/β2)为拉盖尔多项式函数;YLML(Ωp)为球谐函数. 立体谐振子多项式YLM(p)和球谐函数的关系为YLM(p)=|p|LYLML(Ωp). 在Jacobi 坐标系中, 重子的ρ分量和λ分量的相对动量分别为

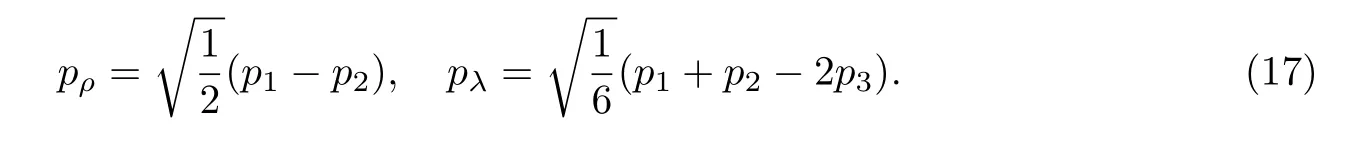
重子在3P0模型框架下强衰变的更多细节可参考文献[10,11,18,24,28-30].

3P0模型除了具有自身内在的不确定性外, 还存在以下几类不确定性: 真空中夸克对产生强度γ、非相对论近似, 以及将SHO 函数作为强子空间波函数和β的取值. 这些不确定性会使在3P0模型框架下计算得到的衰变宽度与实验数据存在2～3 倍的偏差[11], 但对分支比的影响不是很大.

3 数值结果

3.1 参数的选取

对不同的轨道激发模式, 取不同的谐振子参数βρ和βλ. 当初态粒子Λc(2880)+处于:①轨道λ激发模式, 即lλ= 2 激发时, 取βρA= 600 MeV、βλA= 400 MeV; ②轨道ρ激发模式, 即lρ= 2 激发时, 取βρA= 500 MeV、βλA= 450 MeV; ③轨道lρ=lλ= 1 激发模式时,取βρA=560 MeV、βλA=430 MeV.

对末态Σc重子, 取βρ=600 MeV,βλ=430 MeV; 对p质子(或n中子), 取βρ=450 MeV,βλ=470 MeV; 对D介子, 取β=450 MeV; 对π介子, 取β=500 MeV. 本工作取真空中夸克对的产生强度γ=13.4[11,18,31],γ被视为3P0模型中的一个普适常数. 谐振子参数β的取值主要参考文献[11,18].

本工作根据粒子数据库(particle data group, PDG)给出衰变宽度计算过程中涉及的重子和介子的质量, 如表3 所示.

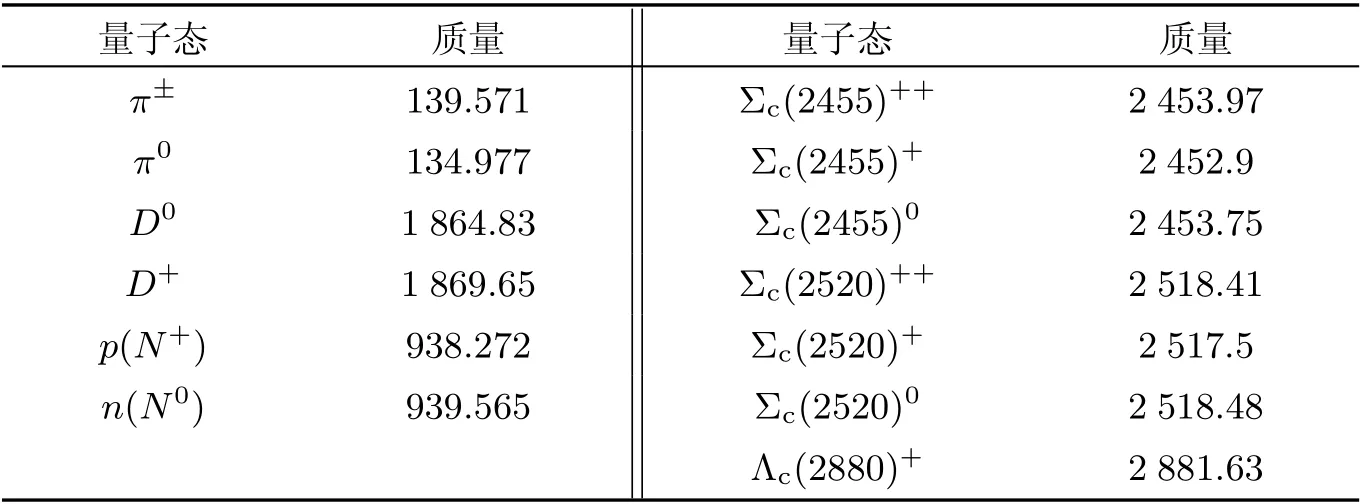
表3 衰变过程涉及的重子和介子的质量Table 3 Masses of involved mesons and baryons in the decays MeV

3.2 Λc(2880)+2D 激发态的强衰变

目前, 理论预测的2D 波Λc重子的质量如表4 所示. 可以看出: 这些数据在理论计算过程中, 认为Λc重子中的2 个轻夸克处于基态, 即只考虑了3 个重夸克和2 个轻夸克整体之间的轨道和径向激发. Kim等[34]在非相对论势模型下计算了Λc/b和Ξc/b的质量谱. 结果显示, 当采用不同方法取参数时, 理论得出的Λc重子质量会有明显差异, 且随着激发态能级的升高, 这种差别会更大. 由此可以看出, 从质量角度考虑无法完全排除Λc(2880)+为2D 激发态的可能. 但若不考虑质量, 仅从衰变性质上考虑, 则Λc(2880)+有可能是2D 激发态.

表4 理论预测2D 波Λc 重子的质量Table 4 Predicted masses of Λc baryons as 2D wave MeV

关于Λc(2880)+2D 激发态衰变宽度的详细计算结果如表5 所示. 表中也给出了DN 道的分支比B=Γ(Λc(2880)+→DN)/Γtotal和分支比比值R=Γ(Λc(2880)+→Σc(2520)π)/Γ(Λc(2880)+→Σc(2455)π).

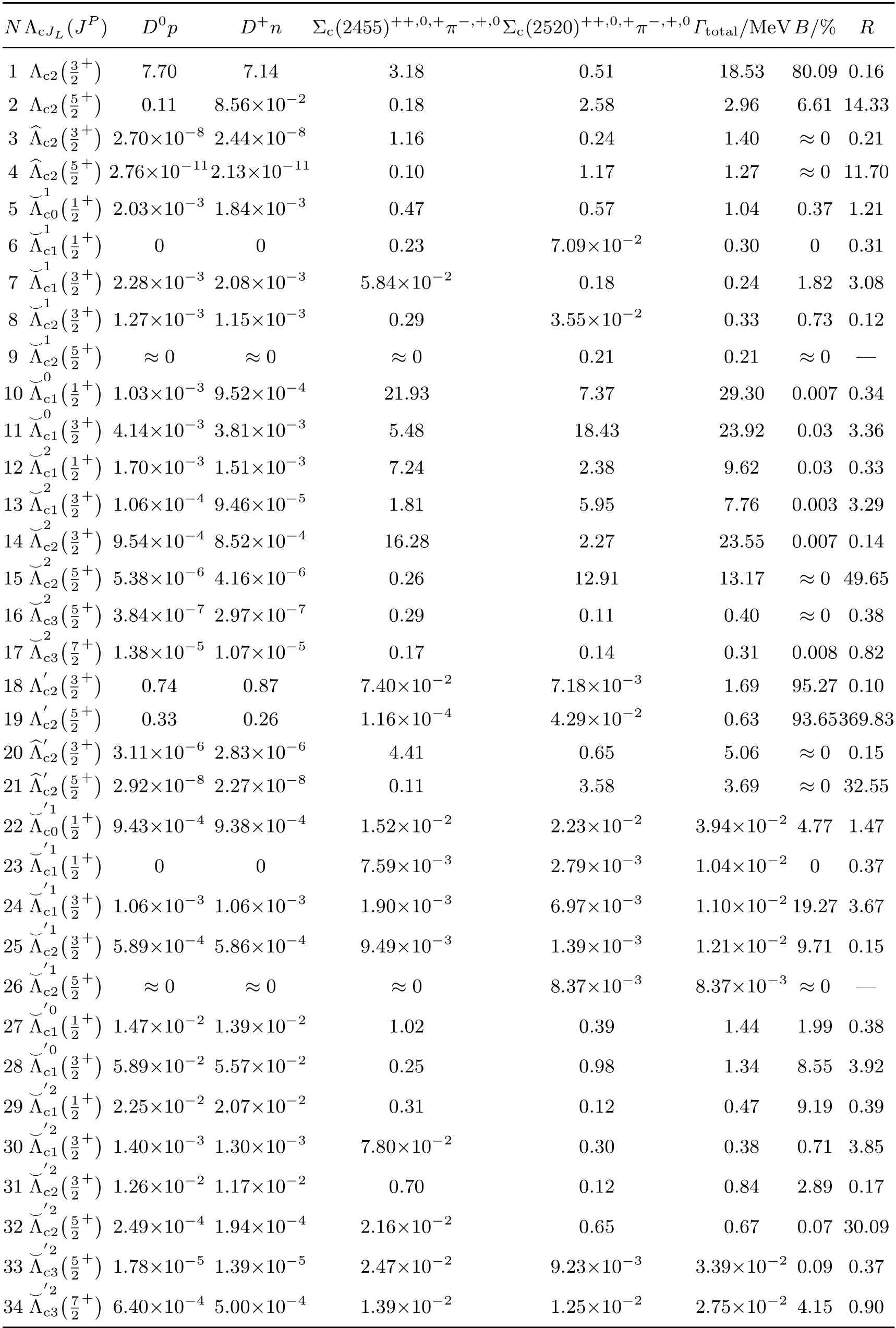
表5 Λc(2880)+2D 激发态的衰变宽度Table 5 Decay width of Λc(2880)+ as 2D-wave excitations

4 结束语

本工作计算得出Λc(2880)+的2 个可能的量子态都为lρ= 0、Sρ= 0, 且DN 道都是其主要衰变道. Λc(2880)+作为2D 激发的重子, 其内部2 个轻夸克的自旋和角动量都为0, 即2 个轻夸克之间没有轨道激发(lρ= 0), 只有径向激发(nρ= 1). 这2 个轻夸克可能形成了两夸克对, 并在衰变过程中保持了两夸克对, 因而DN 道成了主要的衰变道.

理论上还需要在更多模型内进行Λc(2880)+的强衰变研究, 以便进行交叉验证. 实验上也需要更精确的分支比测量数据和JP量子数的直接测定.