回声信号处理综合实验设计及实现

栗学丽

(山东大学 微电子学院， 济南 250101)

卷积和相关是“数字信号处理”课程中非常重要但容易混淆的知识点，它们的物理含义截然不同，但由于它们的公式非常接近，造成许多学生将它们混为一谈，不知如何实际运用这两个概念[1]。下面设计了一个回声信号处理的综合实验，将卷积和相关的理论应用到实际，帮助学生厘清概念并能运用理论解决实际问题。

LabVIEW采用图形化编程，具备强大的信号处理、数据分析等功能，可以方便快捷建立用户界面，使得学生将更多的精力放在实验数据的分析上[2-3]，所以实验采用LabVIEW编程实现。

1 卷积与相关的概念

卷积与相关都分线性卷积和圆周卷积、线性相关和圆周相关，圆周操作是对线性操作进行周期延拓求和得到，是线性操作的一种快速求解方法[4]，所以只讨论它们的线性操作，下文中的卷积和相关都是指线性卷积和线性相关。

卷积和相关有类似的数学公式[5]，设x(n)、y(n)分别表示两个实数能量信号，则

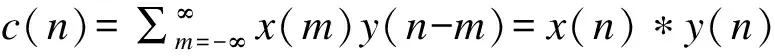
(1)

(2)

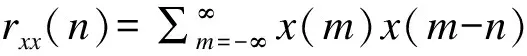
(3)

式(2)还可写为

(4)

进一步若y(n)为实偶信号，则y(-n)=y(n)，这时相关与卷积的公式形式上完全一样，学生就会误认为这两个概念是一样的，就连许多深度卷积神经网络研究人员也对这两个概念一头雾水。深度卷积神经网络最初起源于卷积网络[6]，由于图像处理中许多核函数是对称的，反折后与它本身相同，就省去反折操作，演变成现在的信号与核函数的操作形式是求相关，造成初学者认为卷积与相关是一个概念。

其实卷积与相关的物理概念、实现方法、性质、应用都不同。卷积用于已知输入信号和系统单位冲激响应，求系统的输出信号。根据式(4)相关是第二个信号反折后与第一个信号求卷积，卷积本身还有一个求反折的过程，所以第二个信号两次反折后就是原信号本身，也就是第二个信号直接移位，与第一个信号对应项进行运算，是比较两个信号的相似程度。

回声是一种常见生活现象，它是原声音信号经过一系列反射之后，又被发音者听到，造成听觉混淆。可以对这一现象运用卷积和相关理论分析和解决问题。如果已知原始语音和回声产生系统的单位冲激响应，就可以用卷积得到回声信号。再如，已知原始语音和回声信号，可以通过互相关它们的相似程度，进而推算出原信号与障碍物之间的距离，这也是声源定位[7]所依据的原理。

下面就设计了一个回声信号处理的综合实验，包括回声产生、回声特性分析、回声消除三部分，分别运用卷积、自相关及互相关、卷积(逆滤波)的理论并用LabVIEW编程实现，通过实例将卷积和相关的理论应用到实际，帮助学生理解运用。

2 回声信号处理综合实验设计及LabVIEW实现

2.1 回声产生

回声产生的差分方程表示为：

c(n)=x(n)+αx(n-D)+βx(n-2D)+γx(n-3D)+…

(5)

x(n)为原始语音，c(n)为生成的回声，D为回声的延迟量，α、β、γ等为多次回声的衰减系数，一般0<…<γ<β<α<1。令β=γ=…=0，可以得到一次回声产生的简化模型：

c(n)=x(n)+αx(n-D)

(6)

相应的系统单位冲激响应表示为

h(n)=δ(n)+αδ(n-D)

(7)

故回声信号还可表示为原始语音与回声产生系统单位冲激响应的卷积，即

c(n)=x(n)*h(n)

(8)

实验要求根据式(8)进行LabVIEW编程，产生回声延迟量和衰减系数都可调的回声信号并试听效果，得出人耳能听出回声效果的最小延迟量。原始语音让学生录制自己的声音，增加趣味性。

实验用户交互界面如图1所示，图中给出的是原始语音“山东大学”(采样频率为8000 Hz)、回声(延迟量为1000个点，衰减系数为0.5)、回声产生系统单位冲激响应的波形图。卷积通过调用LabVIEW的Convolution.vi节点实现。

通过这个实验，学生掌握了回声信号产生的卷积方法，通过调节回声延迟量和衰减系数，从视觉、听觉感受到卷积带来的不同效果，趣味性强，学生印象深刻。

图1 回声产生界面

2.2 回声特性分析

1)基音周期估计及清浊判断

语音信号是短时平稳信号，一般取20 ms左右为一帧信号，分帧处理。根据发音时声带是否振动，相应的是否产生准周期信号，将语音分为清音和浊音。清音没有周期性，其周期为0。浊音呈现准周期性，其周期是语音识别和合成的重要参数。自相关法为清浊音判断的一种方法[8]。浊音自相关函数具有与原信号相同的准周期性，且它的准周期性更明显、好判断，故实验采用自相关法。

实验要求学生给出任意一帧回声信号的波形图、自相关图，求出其周期，判断清浊性。图2(a)和(b)分别给出起始点在800点的一帧清音信号、起始点在3000点的一帧浊音信号以及它们自相关函数的图形。图3给出一帧信号清浊判断的关键程序，自相关函数通过调用LabVIEW的AutoCorrelation.vi节点得到，周期值主要通过Peak Detector.vi节点运算得到，用户可以在图形界面上用鼠标调节蓝线阈值，得到主次极大值的间隔为周期值，根据周期值范围判断清浊性。

通过这个实验，学生知道了自相关是比较信号及其延迟信号的相似性，对于准周期信号还可以用此法求它的周期。

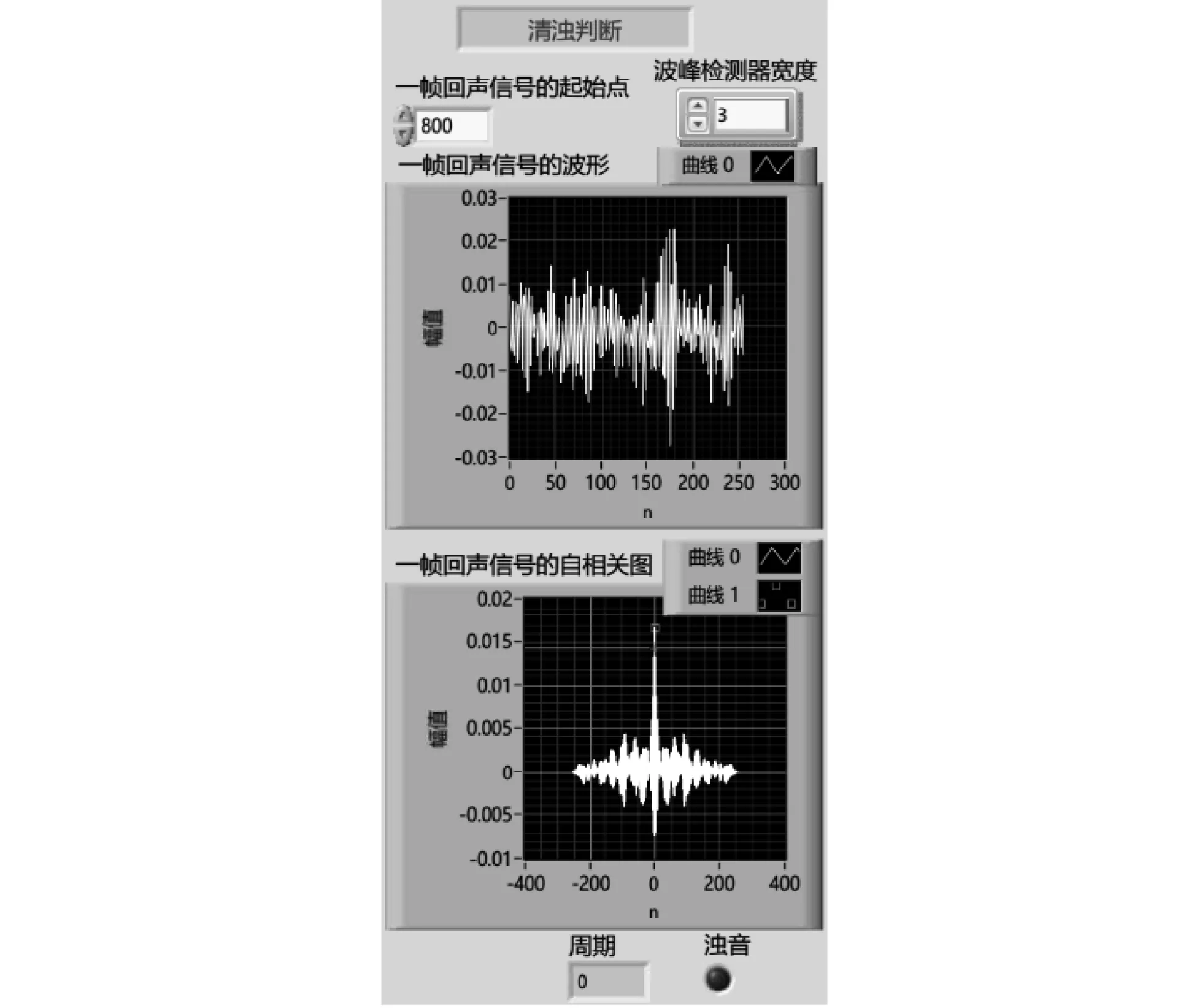
(a)清音

(b)浊音图2 一帧回声信号及其自相关函数的波形

图3 一帧回声信号清浊判断的关键程序框图

2)延迟量估计

实验要求分别用自相关法和互相关法求出回声延迟量，并进行比较，理解相关的性质。其一，自相关法。根据回声是原始语音经过一段时间延迟后叠加得到的，将回声延迟同样的时间求它的自相关会出现一个极大值，从而估计出回声的延迟量。实验结果如图4的回声自相关图和延迟量所示，编程方法与图3相似。

图4 回声参量估计

其二，互相关法。同样根据回声是原始语音经过一段时间延迟后叠加得到的，这时求回声和原始语音的互相关，在延迟时刻就会出现一个极大值，从而估计出回声的延迟量。实验结果如图4回声、原声互相关图和延迟量2所示，互相关函数通过调用LabVIEW的CrossCorrelation.vi节点得到。

通过这个实验，学生就会发现自相关法和互相关法都能正确求出回声的延迟量参数，但自相关图形是偶对称的，互相关不具备对称性；自相关法只需要一个回声信号，互相关法除了回声信号，还需要知道原始信号。从而学生能进一步理解自相关和互相关的性质。

3)衰减系数估计

实验要求估计出回声的衰减系数，并与真实值比较，分析误差原因。

根据式(3)和式(6)可得

rcc(n)=(1+α2)rxx(n)+αrxx(n-D)+αrxx(n+D)

(9)

考虑到自相关函数衰减性，忽略掉rxx(D)和rxx(2D)，得

(10)

rcc(0)和rcc(D)可以通过上述自相关法得到，则衰减系数α通过求解式(10)一元二次方程的根得到，在LabVIEW中调用Polynomial Roots.vi节点实现，因为0<α<1，舍弃不符合此条件的根值，得到衰减系数估计值。此实例α的真实值为0.5，图4估计出的值为0.45，有误差，是因为式(10)是简化运算得到的。

通过这个实验，将理论运用到实际，能锻炼学生解决实际问题能力。

2.3 回声消除

回声消除就是要求从回声中恢复出原始信号，尽量减小失真。

由于回声是由式(8)得到的，所以

x(n)=c(n)*h-1(n)

(11)

h-1(n)是回声产生的逆系统——回声消除系统的单位冲激响应，记g(n)=h-1(n)，得

h(n)*g(n)=δ(n)

(12)

进行z变换，得

H(z)G(z)=1

(13)

(14)

(15)

在LabVIEW里可以通过调用MathScript节点impzd函数得到回声消除系统的单位冲激响应，再调用卷积Convolution.vi节点得到回声消除后的语音。

通过这个实验，学生再次体会到卷积的作用，将卷积与相关彻底分清楚。学生开始做实验时，用impzd(b,a)求得g(n)，b、a分别对应式(14)分子、分母系数。细心的学生发现消除回声效果不是太好，是衰减系数的误差引起的吗？将真实值代入衰减系数，发现还有个别音效果不好，这是什么原因呢？观察回声消除系统的单位冲激响应波形图，发现它只给出前两个非零值，而由式(15)可知g(n)是无限长的，省略后面非零项还是很有影响的。将它改为impzd(b, a, 5*l)，l=D+1，求出前5个非零项，仅是对后面接近零的极小项进行舍弃，这时再听消除效果就很好。

图5给出回声消除LabVIEW关键程序框图。回声消除后的语音是用式(11)卷积实现的，理想的回声消除后的语音是用衰减系数真实值，通过无限长冲激响应滤波器IIR Filter.vi逆滤波实现的，以此作为参考。滤波器逆滤波是通过差分方程递推计算实现的，它避免了卷积无限长单位冲激响应需要截断引起的误差。虽然它也会有小的累计误差，但它运算量小，速度快，精度高。

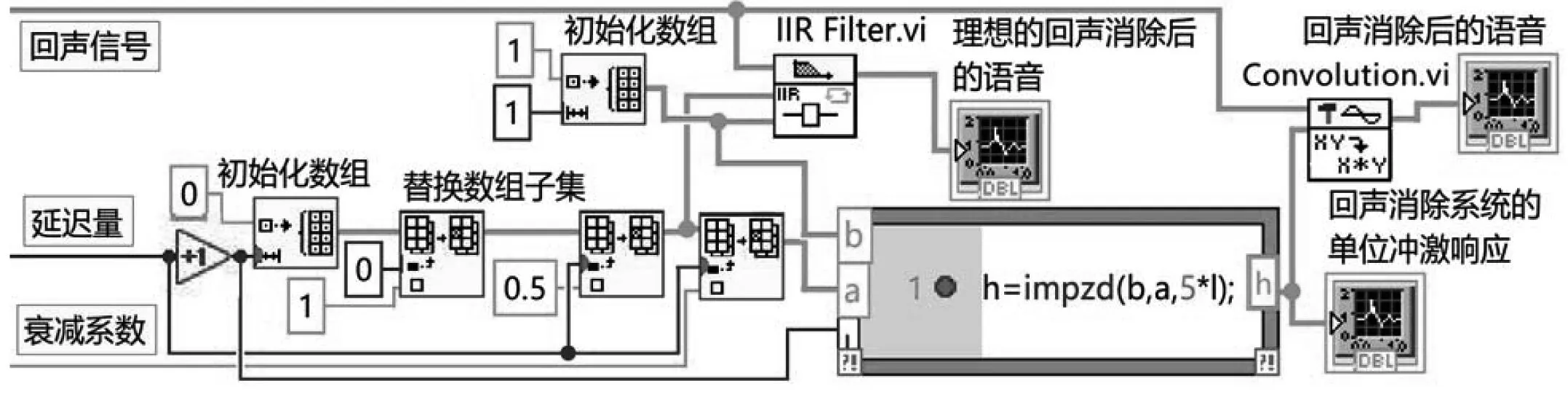
图5 回声消除的关键程序框图

通过这个实验，学生不但更深一步理解了卷积，而且通过发现问题、解决问题，明白滤波也是一种输入到输出的操作。输出可以通过用输入卷积系统单位冲激响应得到，也可以利用差分方程递推计算得到。

2.4 实验讨论

实验最后，要求学生总结卷积与相关的不同，进行实验拓展——如对于多次回声，如何实现；对于回声参数估计、回声消除，还有何种方法。引导学生举一反三进行推广向学有余力的学生推荐关于广义互相关、自适应回声消除等方面的文献，拓展学生的知识面，提高学生的创新能力和综合素质。

3 结语

针对学生对卷积和相关概念不清的问题，结合生活现象，设计了回声产生、回声特性分析、回声消除的综合实验，将难以理解的卷积、自相关、互相关等概念有机地串在一起。实验要求设计交互性好、便于比较的用户界面，文中给出LabVIEW实现的关键程序和界面。实践表明，理论和实验相辅相成，帮助学生理解和运用。学生在做与生活密切联系的实验时，兴趣更高，愿意进一步探索，能真正将理论知识得以内化，学以致用，教学效果好。