对《电磁波衰减系数特性分析》结果的猜想
2017-10-14钟乙源张岩陈兴生李爽
钟乙源,张岩,陈兴生,李爽
(中南大学地球科学与信息物理学院,湖南 长沙 410083)
对《电磁波衰减系数特性分析》结果的猜想
钟乙源,张岩,陈兴生,李爽
(中南大学地球科学与信息物理学院,湖南 长沙 410083)
对陈清礼等提出的“利用超过阈值频率的电磁波进行大深度勘探”的观点进行了深入分析,并提出质疑。主要对陈清礼等观察到的衰减系数高频振荡现象进行了模拟,然后对该现象进行分析,将该现象解释为数值误差造成的假象。给出了一种数值稳定的计算方法,用变换后的方法计算电磁波衰减系数,结果显示电磁波的衰减系数随频率始终递增,并在高频段趋向于稳定值,表明陈清礼等计算的高频衰减现象实际是由数值误差的放大造成的假象;最后,在数学上严格证明了衰减系数的极限随频率增加而收敛于一个正数。
电磁波;衰减系数;数值误差;电磁波勘探
陈清礼等在《电磁波衰减系数特性分析》[1]一文中计算了在1Hz到1015Hz范围内电磁波衰减系数的频率响应。所得结果显示,衰减系数先随频率增大而增大,当频率达到一定程度时衰减系数缓慢增加,接着出现阈值,继续增大频率后曲线发生振荡,继而衰减为零。文献[2]做了定性分析,认为电磁波在超过某一阈值的高频段会出现不衰减现象,并希望通过高频电磁波解决勘探深度和分辨率的矛盾。笔者对该观点存在质疑,提出了不同的看法。
由于电磁波的分辨率和勘探深度往往是不相容的,若有一种方法能兼顾分辨率和勘探深度,那该方法应该经过严格的理论证明。为此,笔者对电磁波衰减系数的高频振荡衰减现象重新模拟并分析,观察到高频段的振荡是跳跃的、不连续的,与计算公式的连续性不符,因此提出猜想:高频的振荡是计算机数值误差引起的。接着分析产生数值误差的因素,对公式进行适当变换以消除误差来源,再用变换后的公式与原公式分别计算在同等参数下衰减系数的频率响应曲线。结果显示:变换公式后计算的衰减系数与原公式计算结果在低频部分(未发生振荡区域)完全重合;而在发生振荡区域,变换后的公式得到的曲线在高频段是平滑稳定的数值,没有出现振荡和衰减,结果与预期一致,证明数值误差的猜想是成立的。为了进一步说明衰减系数在高频时不会产生振荡,对衰减系数求极限,得到当频率趋向于无穷时,衰减系数的极限收敛于一个极限值,该极限值与频率无关。
1 基本理论
已知谐变电场传播的亥姆霍兹方程[2]为:
(1)
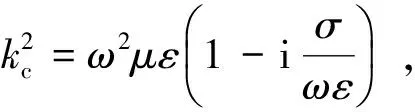
(2)
令kc=k1-ik2,则:
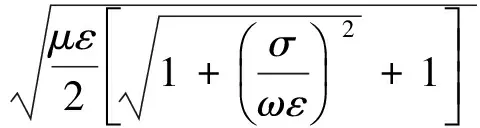
(3)
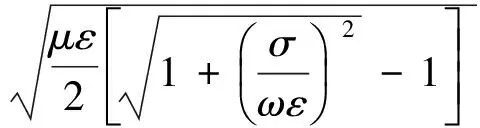
(4)
取Z轴垂直地面向下,X轴、Y轴指向水平方向。不妨令极化方向沿X。在均匀平面波条件下,解得:
(5)
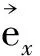
2 振荡原因分析和算法变换
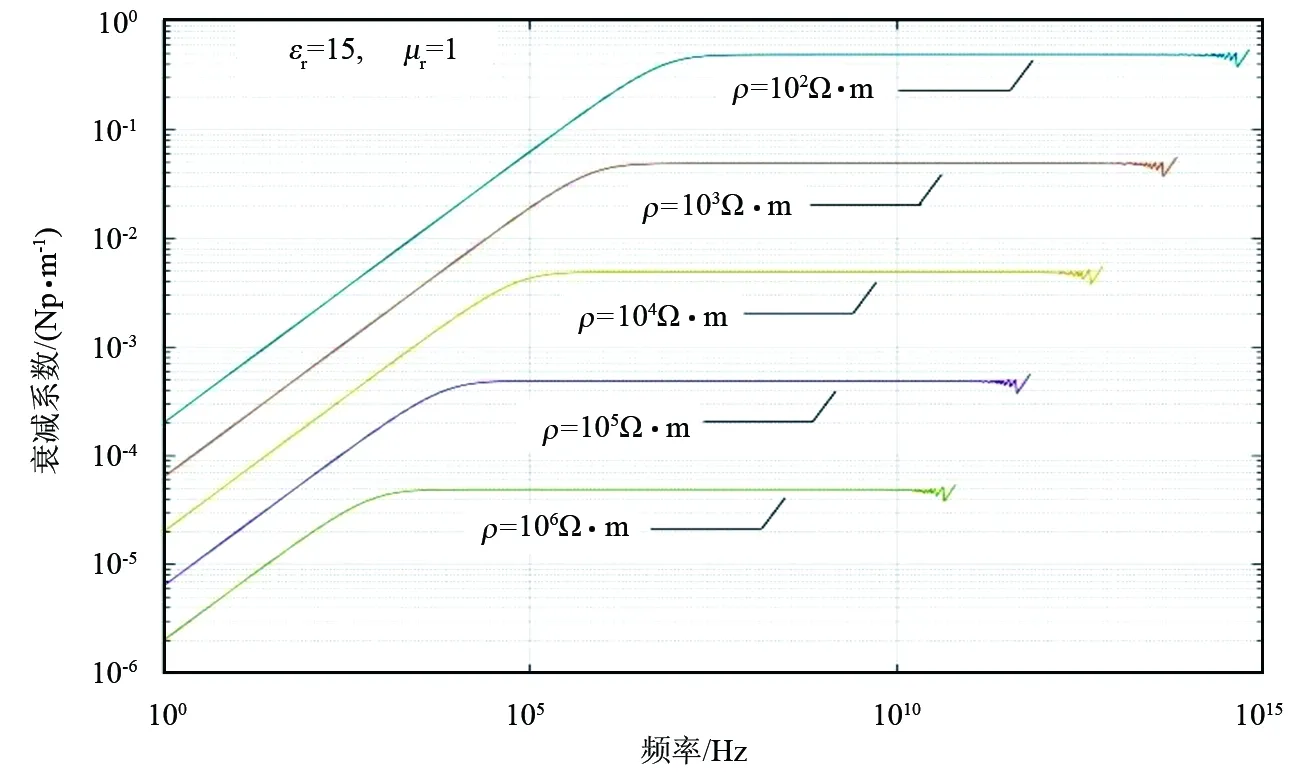
图1 公式(4)计算的衰减系数频率响应曲线
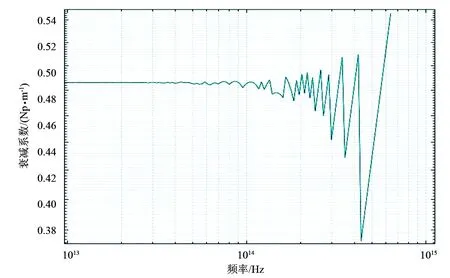
图2 在图1中的ρ=102Ω·m的衰减系数频率响应高频段
先用式(4)计算衰减系数,重现文献[1]中衰减系数在高频段的振荡现象。
选择102、103、104、105、106Ω·m共6组电阻率,给定相对磁导率μr=1,相对介电常数εr=15,根据式计算衰减系数,所得频率响应如图1所示。可以看到,在每一条曲线尾部都出现了振荡,因为振荡部分后面的计算值为0,所以在双对数坐标下不显示。将图1中的ρ=102Ω·m对应的衰减系数频率响应的高频振荡部分放大后观察,如图2所示。
理论上,衰减系数的计算公式是关于ω的连续函数,且在ω≠0处并没有奇点。但是,频率很高时根据式计算的值是0。从图2可以看到,高频时衰减系数是跳变的、不连续的,该种跳变与公式的连续性不符,表明高频时公式的计算值不一定是该式的真实结果,可能存在大的数值误差。
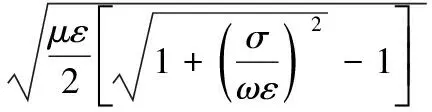
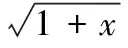
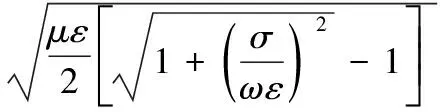
(6)
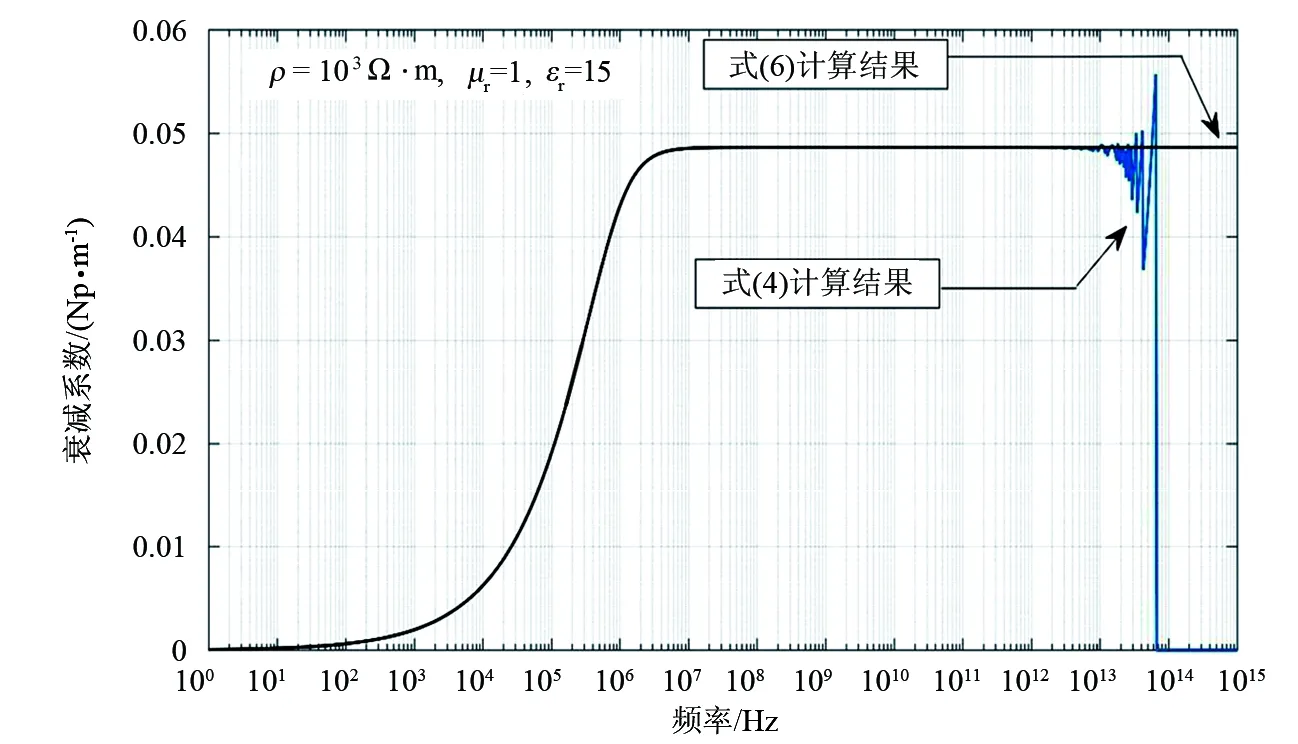
图3 变换后公式与原公式计算的衰减系数频率响应曲线对比
分别用式(4)和变换后的式(6)计算衰减系数的频率响应,取电阻率ρ=103Ω·m,μr=1,εr=15,对比结果显示在半对数坐标中,如图3所示。
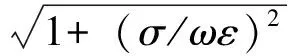
3 衰减系数的极限
上述结果只是在程序计算上给出了一个直观的结果,而没有证明当频率很大时衰减系数是否收敛于非零的极限值。对式(4)取极限:

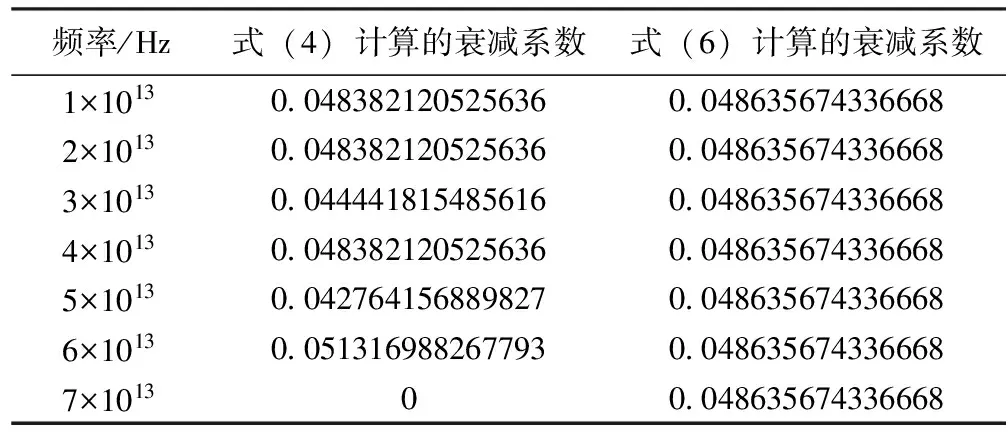
表1 式(4)与式(6)计算的7个频点的衰减系数对比
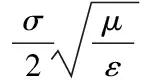
对式(6)取极限也能得到同样的结果。该极限值是一个大于0的数,它与电导率、磁导率、介电常数有关,和频率没有关系。说明当ω增大时,衰减系数会趋向于稳定的值。利用式(4)和式(6)对7个高频率点进行计算,计算结果如表1所示。
4 结论
1)电磁波的衰减系数受频率影响,随着频率增加衰减系数先增大后变平缓,最终达到阈值。
2)文献[1]中计算得到的曲线在高频段产生振荡,是因为原公式中包含两个很接近的数相减,会造成误差的放大。编程计算时应该先对计算公式做变换,避免误差。笔者将两数相减变换成两数相加,可以很好地减小误差。
3)由于文献[1]中衰减系数呈现的“频率超过阈值后衰减”的现象是由于数值误差产生的假象,所以高频时衰减系数依然是一个较大的值,因此文献[1]中“利用大于阈值的电磁波解决勘探深度与分辨率的矛盾”的想法是缺乏理论依据的。
4)衰减系数的极限是一个只与电导率、磁导率、介电常数有关的正数。
[1]陈清礼,肖希,蒋晓斌,等.电磁波衰减系数特性分析[J].石油天然气学报(江汉石油学院学报),2014,36(8):43~51.
[2]杨儒贵.电磁场与电磁波[M].第2版.北京:高等教育出版社,2010:205~208.
[3]李祺.物探数值方法导论[M].北京:地质出版社,1991:12~14.
[编辑] 龚丹
P631.325
A
1673-1409(2017)19-0046-04
2016-06-16
钟乙源(1995-),男,现主要从事电磁勘探方面的学习,18390999216@163.com。
[引著格式]钟乙源,张岩,陈兴生,等.对《电磁波衰减系数特性分析》结果的猜想[J].长江大学学报(自科版), 2017,14(19):46~49.
