基于稀疏系统辨识的改进的零吸引LMS算法*
2022-12-30辛龙坤易胜宏
辛龙坤,孟 金,易胜宏,刘 挺
(重庆邮电大学 a.通信与信息工程学院;b.光电工程学院,重庆 400065)
0 引 言
近些年,自适应滤波算法已广泛应用于通信信号处理[1]、声回波信号抑制处理[2]和自适应降噪处理[3]等。Widrow[4]提出的最小均方(Least Mean Square,LMS)算法,因其结构简单、稳定度高和易于实现,被广泛应用于系统辨识、回波抵消和自适应预测等。学者们研究发现,许多信道具有稀疏性[5-6],其稀疏性指信道的大部分冲激响应为零或接近零,少部分冲激响应为有效值。常规的LMS算法并没有结合这种稀疏特性,导致其稳态均方差(Mean Square Deviation,MSD)和收敛速度并不好。因此,Chen等人[5]提出了将l1-norm惩罚引入LMS构成零吸引LMS(Zero-attracting LMS,ZA-LMS)和重新加权零吸引LMS(Reweighting Zero-attracting LMS,RZA-LMS)算法,使算法在估计零冲激响应时,滤波器所估计的值更加接近稀疏信道的冲激响应值。但ZA-LMS算法没有分辨信道冲激响应值的大小,对所有的信道冲激响应都采用同样大小的零吸引权重,导致其MSD只比常规的LMS算法略好;RZALMS算法在估计信道中较小冲激响应时,其零吸引函数的权重值较大且不易调整,导致其MSD并未达到系统的最佳值。因此,Gu等人[6]提出将l0-norm惩罚与LMS算法结合构成l0-LMS算法。该算法只对较小的冲激响应进行一个向零吸引的处理,在每一次迭代更新中滤波器的零系数与信道的零冲激响应的差值都较小,使其误差信号值较小,从而对信道的较大冲激响应的估计更为合理。但该算法并没有对较大的冲激响应进行适宜的处理,导致其收敛速度有待进一步提升。随后,学者们提出了一种lp-LMS算法[7-9],该算法引入了lp-norm惩罚,通过调节参数p获得了比l0-norm和l1-norm算法更好的MSD值,但是该算法存在有实时的除法、指数和指数幂运算[7],导致其复杂度相较于l0-norm和l1-norm算法成几何增长,故该类型算法不在本文中考虑。
本文提出将一种先将RZA-LMS与l0-LMS算法相结合再进行改进的IZA-LMS(Improving ZA-LMS)算法。该算法先保留了RZA-LMS算法对较大冲激响应处理的零吸引函数,以保留较快的收敛速度;再对l0-LMS算法对零冲激响应处理的零吸引函数进行改进,使所提算法比l0-LMS算法具有更快的收敛速度和更低的MSD。
1 系统辨识模型
本文的研究基于图1给出的系统辨识模型[10],该模型指由一组已知的输入信号X(n)经过与稀疏信道的冲激响应H(n)=[h0h1…hL-1]T(L为信道的阶数)相乘,再加上环境噪声信号n0(n),得到期望信号d(n);输入信号X(n)与一个自适应滤波器的系数W(n)=[w0w1…wL-1]T相乘得到输出信号y(n),再将期望信号d(n)与输出信号y(n)作差得到误差信号e(n),将根据该值对自适应滤波器的系数W(n)进行迭代更新,使滤波器的系数W(n)无限的逼近稀疏信道的冲激响应H(n)。
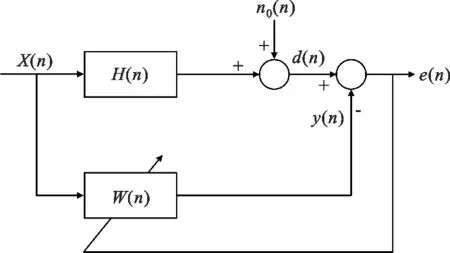
图1 系统辨识模型
2 现存的稀疏LMS算法
2.1 ZA-LMS与RZA-LMS算法
稀疏自适应滤波算法的差异主要是迭代更新公式中的零吸引函数不同。由此,ZA-LMS算法的迭代更新公式如下:
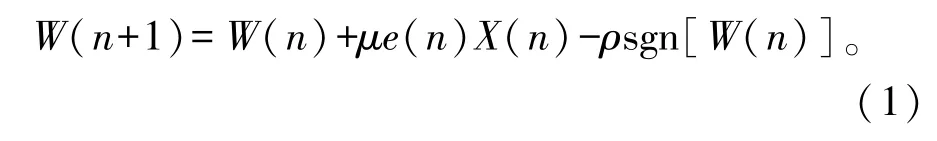
式中:μ为步长因子,以调整每一次迭代更新的值;ρ为零吸引子权重,以调节零吸引函数值的大小;sgn[W(n)]为
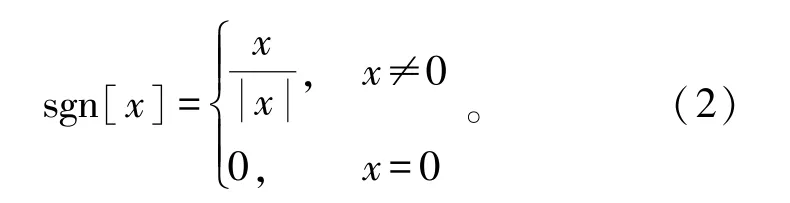
虽然ZA-LMS算法的MSD值比LMS算法更低,但是它的零吸引函数对所有的冲激响应都采用了同样大小的零吸引权重值,导致MSD并未达到系统的最佳值。因此,RZA-LMS算法被提出,其迭代更新公式如下:
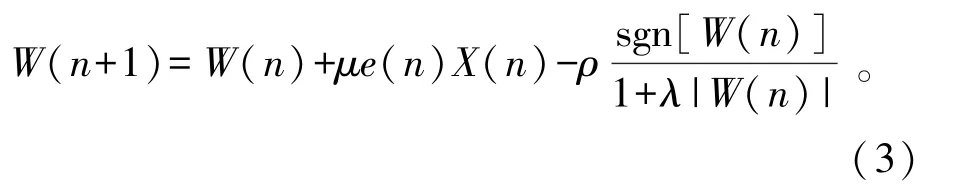
式中:ρ为零吸引子权重;λ为区分参数,以区分不同大小的冲激响应,使零吸引函数采用不同大小的零吸引权重值,得到比ZA-LMS算法更低的MSD值。但该算法估计较小的冲激响应时,其零吸引强度较小,导致滤波器估计的较小系数值与对应信道冲激响应的差值较大。
2.2 l0-LMS算法描述
l0-LMS算法的零吸引函数只对较小的冲激响应进行零吸引处理,其迭代更新公式为
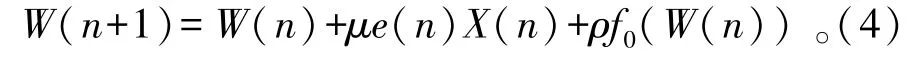
式中:ρ为零吸引子权重;f0(W(n))为f0(W(n))=[f0(W0(n))f0(W1(n)) …f0(WL-1(n))]T;f0(Wi(n))为
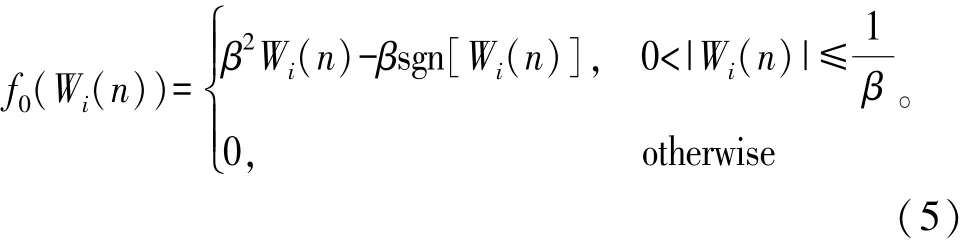
式中:β为调谐参数,以调整零吸引函数的值。该算法虽然对较小的冲激响应处理较为优秀,获得了比RZA-LMS算法更低的MSD值,但该算法并未对较大的冲激响应做任何处理,导致其收敛速度不及RZA-LMS算法。
3 所提的IZA-LMS算法
3.1 IZA-LMS算法的描述
本文提出将RZA-LMS与l0-LMS算法结合的IZA-LMS算法,该算法集成了RZA-LMS算法的快速收敛速度和比l0-LMS算法更低的MSD值。所提算法的迭代更新公式为

式中:μ为步长因子;f1(W(n))为f1(W(n))=[f1(W0(n))f1(W1(n)) …f1(WL-1(n))]T;f1(Wi(n))为
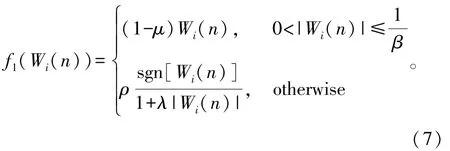
式中:ρ为零吸引权重;β为调谐参数,以调整零吸引函数的值;λ为区分参数,以区分不同大小的冲激响应后,使零吸引函数采用不同大小的零吸引权重值。
图2所示,ZA-LMS的零吸引函数对所有的冲激响应都采用同样大小的零吸引强度,导致MSD的性能不好;RZA-LMS的零吸引函数在对较小的冲激响应处理的零吸引强度较小,导致滤波器的估计系数与稀疏信道的较小冲激响应的差值较大;l0-LMS算法只对较小的冲激响应采取较大的零吸引强度,但是并未对较大的冲激响应进行处理,导致其收敛速度不足。而本文所提出的IZA-LMS算法对估计较大的冲激响应时采取较小的零吸引强度,以获取较快的收敛速度;针对较小的冲激响应时采取较大的零吸引强度,以得到滤波器估计的系数与稀疏信道的冲激响应较小的差值。

图2 几种算法的零吸引函数
3.2 IZA-LMS算法的稳态分析
图1所示,考虑一个稀疏系统辨识模型,其期望信号d(n)为

输出信号y(n)为

期望信号d(n)与输出信号y(n)的差值误差信号e(n)为
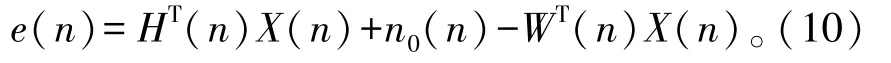
假设稀疏信道的冲激响应与估计滤波器的系数误差为
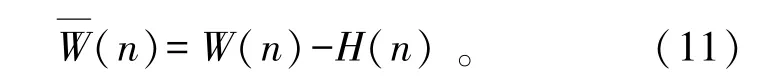
由此,稳态均方差MSD的计量准则如下:

式中:Tr(·)表示矩阵的迹。由此,稳态均方差MSD的计算如下

将式(6)、(7)、(10)代入式(11),其滤波器的系数与稀疏信道冲激响应的误差迭代更新为
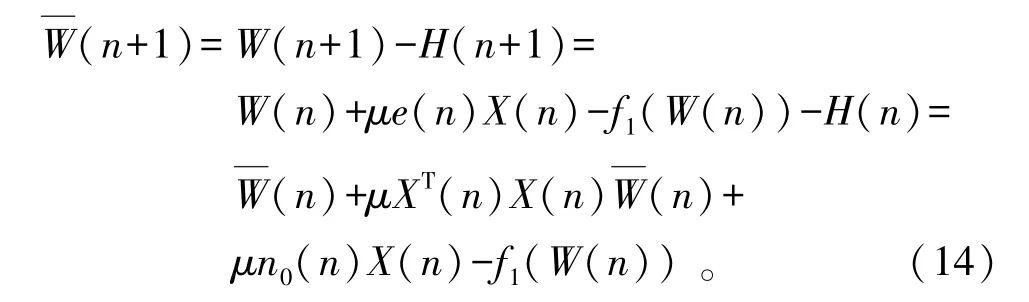
由此,将式(14)代入式(13)可得稳态均方差为
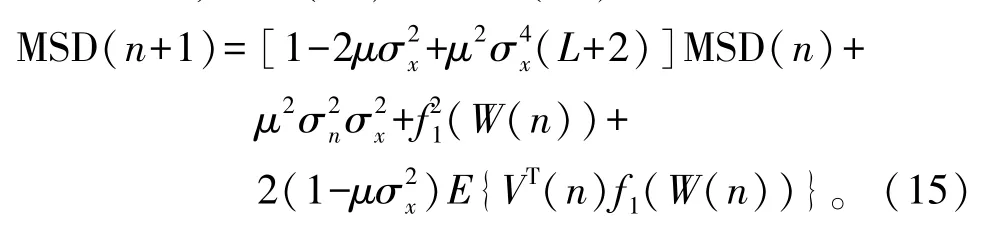
式中:为输入信号X(n)的功率;为噪声信号n0(n)的功率;L为信道的阶数。IZA-LMS算法的MSD由步长因子、输入信号功率、噪声功率以及稀疏信道的冲激响应值所共同决定。根据式(15),当稳态均方差趋于稳定时,步长因子因满足
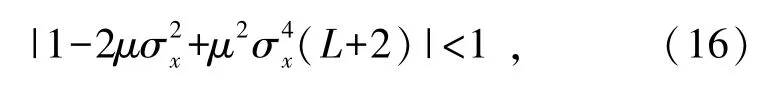
即步长因子μ的取值范围为

因此,当IZA-LMS算法的步长因子选取在上述范围,算法可稳定运行。
4 仿真分析
本文仿真主要基于图1的稀疏系统辨识模型。为了便于对比上述算法的性能,设置功率为=1的高斯信号为输入信号X(n),设置所有算法的步长因子μ=0.005,λ=10,信道的阶数L=128,信噪比20 dB。由此,先确定了系统环境参数,再进行算法的参数对比选择。
4.1 算法参数的确定
上述算法的仿真参数如表1所示。

表1 算法的参数选择
主要对表1中零吸引权重ρ和调谐参数β的最佳参数进行仿真,其具体的稳态MSD仿真结果如图3和图4所示。
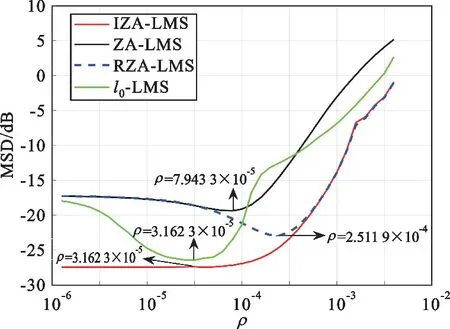
图3 算法不同零吸引权重ρ的MSD曲线图

图4 算法不同调谐参数β的MSD曲线图
由图3可知,IZA-LMS算法的零吸引权重ρ的有效范围远比其他算法更广且MSD值更低,ZALMS、RZA-LMS、l0-LMS和IZA-LMS算法的最佳零吸引权重分别为ρ=7.943 3×10-5、ρ=2.511 9×10-4、ρ=3.162 3×10-5和ρ=3.162 3×10-5。
由图4可知,当调谐参数β值过大时,所提IZALMS算法的MSD性能都比基础的LMS更好,而现存的l0-LMS的MSD性能比基础的LMS都差,即所提出的IZA-LMS算法的调谐参数β的适用范围比l0-LMS算法更广和更具有吸引力。在后续仿真中,设置最佳的调谐参数为β=100。
4.2 步长因子的仿真对比
为了进一步确定算法的步长因子对算法性能的影响,采用4.1节中得到的各个算法的最佳零吸引权重值,并设置调谐参数β=100。图5给出了上述参数的MSD仿真对比。
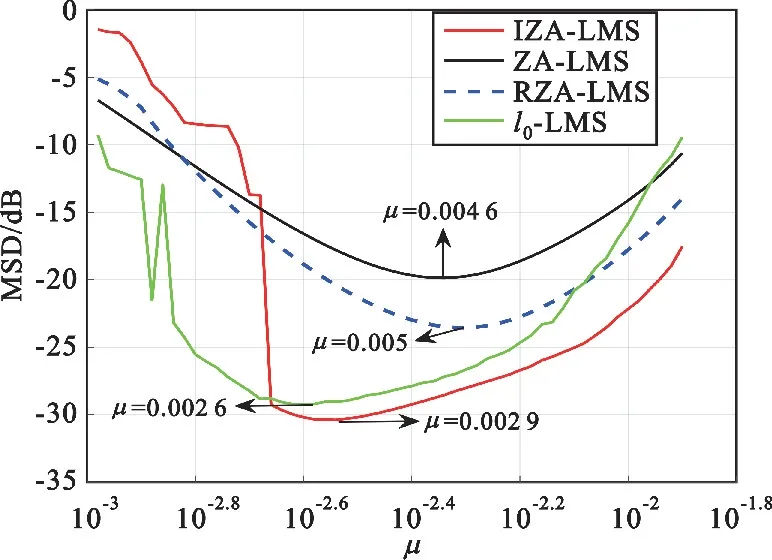
图5 算法不同步长因子μ的MSD曲线图
如图5所示,当步长因子μ较小时,所有算法的MSD都并没有达到最佳值,ZA-LMS、RZA-LMS、l0-LMS和IZA-LMS算法的最佳步长因子分别为μ=0.004 6、μ=0.005、μ=0.002 6和μ=0.002 9。
4.3 稀疏信道下的仿真对比
采用4.1节和4.2节中各个算法的最佳参数,假设非零冲激响应有P个,仿真稀疏信道的非零冲激响应个数分别设置为4、8、16,与图6的稀疏信道进行仿真对比。稳态MSD的仿真如图7所示,图7的每个数据点都经过了100次蒙特卡洛模拟。
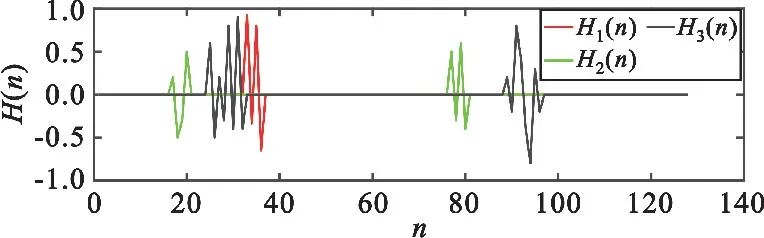
图6 多种稀疏信道的冲激响应
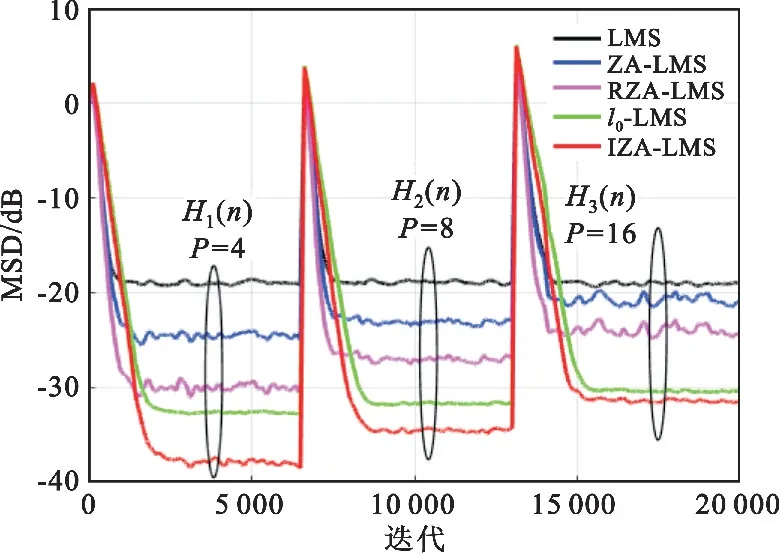
图7 算法的MSD曲线仿真图
由图7可知,三种稀疏信道下,所提的IZA-LMS算法都保持着最低的稳态MSD。当稀疏信道越稀疏时,IZA-LMS算法的稳态MSD表现得越低,比现存的l0-LMS算法的MSD低5 dB。在辨识稀疏信道时,所提的IZA-LMS算法比ZA-LMS、RZA-LMS和l0-LMS算法更具有优势。
5 结 论
本文提出了一种RZA-LMS算法和l0-norm类型相结合的IZA-LMS算法,对该算法进行了理论稳态MSD的分析,并给出了步长因子、零吸引权重和调谐参数的选择。仿真结果证明了该算法不仅具有RZA-LMS算法的快速收敛特性,而且其稳态MSD还比l0-LMS算法更低。
