运动中人体信道数学模型研究

王紫阳 廖薇

摘 要：人体周围传感器共同组成的体域网（BAN）可实时观察并记录人体运动、休息等正常活动时生理参数的变化。对人体运动带来的信道特性变化进行分析是扩展体域网络应用的重要工作。采用两步法构建运动人体信道数学模型。通过电磁仿真得到人体跑步中连续9个动作模型数据，然后通过统计学拟合得到人体连续动作的累积分布模型。实验结果表明，人体跑步动作会改变路径增益，但不会影响信道稳定性。运动中信道增益遵循正态分布，可将衍射等效应认为是乘以变化的统计随机量。而峰值路径的出现时间总体呈逆高斯分布，为直射基频分量与高频分量叠加的结果，实务中须对此加以考虑。

关键词：人体通信;时域有限差分;冲激响应;电容耦合;无线体域网

DOI：10. 11907/rjdk. 201235                                                                  开放科学（资源服务）标识码（OSID）：

中图分类号：TP303   文献标识码：A                 文章編号：1672-7800（2020）011-0075-04

Mathematical Model of HBC Channel in Motion

WANG Zi-yang，LIAO Wei

（School of Electronics and Electrical Engeering，Shanghai University of Engineering Science， Shanghai 201620，China）

Abstract： The body area network （BAN） which is composed of sensors around the human body can observe and record the changes of physiological indexes during normal activities such as human movement and rest in real time. For the network widely used in body area， the analysis in human motion characteristic change is more important. In this paper， the mathematical model of human channel in motion is obtained by two-steps method. Through electromagnetic simulation， the data of nine continuous motion models in human running are obtained， and then the cumulative distribution model of human continuous motion is obtained by statistical fitting. The results show that human running motion can change the amplitude， but does not affect the channel stability. The channel gain in motion follows the normal distribution， and the diffraction and other effects can be considered as multiplying the variation of statistical random quantity. However， the occurrence time of peak path is inverse Gaussian distribution which is the result of superposition of direct fundamental frequency component and high frequency component， and this should be considered in real life.

Key Words： human body communication; finite difference time domain; impulse response; capacitive coupling; body area network

0 引言

随着体域传感器网络与体表智能实时监测微系统的不断发展，人体通信技术成为医工结合的崭新研究领域，智能假肢、康复训练机器人等技术对人体区域通信技术提出了更高要求。保证体域网发展及人体区域内通信网络的稳定及高速率传输成为该技术得以实际应用的关键[1]。人体通信技术使用人体作为通信媒介，将信号耦合到体表，可实现低功耗、高速率传输，因其频率的特殊性不会对人体自身安全产生明显影响。

由于人体介质的复杂介电特性、人体肢体及各种器官的存在及人体表面形状的复杂性，造成电磁波在人体表面存在绕射、散射等特性。对于人体通信频段，电磁波在人体周围主要以表面波形式传播[2];文献[3]阐述UWB频段体表传感器传播特性，以表面波的方式研究电磁波在人体表面皮肤的传播机理;文献[4]通过仿真建立人体通信的电路模型，得出人体等效电路具体结构及详细参数;文献[5]研究手臂及发射极处于不同位置下的传播信道;文献[6]研究人体摆臂动作，并对该动作的变化单独建立模型。上述研究对于可穿戴设备的实际应用及体域网实时信息交互还远远不够。为考量人体活动的不规律性对信道的可能影响以及进一步应用人体通信设备，需要对生活中人体的整个动作进行研究分析。本文通过两步法构建运动中的人体模型，通过电磁仿真得到人体连续跑步动作的仿真模型，采用统计学拟合构造运动中人体信道模型。

1 人体介电特性

人体组织介电特性会随着频段的不同产生不同的生物特性。通过分析人体组织在介电谱中的色散现象，本文基于介电特性与频率之间的关系构建模型。采用CST软件构建仿真环境，背景材料设置为与空气中电磁环境相同的开放环境，人体模型参数采用最接近实际情况的一阶德拜公式（Debye），模拟人体电磁特性如下：

εr（ω）=ε∞+χ（ω）+σ0jωε0     （1）

式（1）中第一项为频率趋于无限大时人体的相对介电常数，后两项用于描述人体组织介电谱中的色散现象，用于人体介电常数建模。

采用包含51种人体组织模型，该模型基于亚洲成年人身体尺寸统计数据库构建，各组织相对介电常数及电导率来自文献[7]，空间分辨率为2mm。采用计算机工具构造人体模型的身体姿势及移动姿势，人体的奔跑動作主要集中于双手摆臂及双腿大幅度运动过程中，故模型设置中保持腰部及头部姿势不变，减少不同关节表面散射及折射的干扰。将所设发射极置于心脏前端，与已有人体通信ECG检测设备相结合[8]。为了贴近实际，发射极与接收极定义为3cm×3cm的两片电极片，电极片间隔5cm，信号采用二阶高斯脉冲。为便于观察，将所有端口的输入输出信号归一化到50Ω以模拟实际电极片情况。连续人体运动模型如图1所示。

2 连续动作模型仿真

在人体周围的移动通信系统中，发射极信号会通过多种方式和路径到达接收端，即多径效应。由身体活动带来的体表多径效应，往往集中于直射电磁波产生的短暂遮挡效应过程，故而引起接收信号的幅值及相位发生波动，导致不同程度的路径延迟。

h（t）=F-1{H（f）}=F-1{Fvr（t）Fvt（t）}     （2）

公式（2）所示为仿真信号处理过程。对于时域脉冲信号，将输入、输出电压进行傅里叶变换，在频域范围内得到信号的延迟效应，再进行反傅里叶变换将信号转换到时域，得到时域范围内的冲激响应曲线。接收器放置在右胸、左腰、右腰及双耳，形成5条通信传输链路，这5条链路不会随着跑步姿势的变化产生距离上及空间位置的变化，同时这5条典型链路可以代表体表上所有直射链路。5条链路具有完全不同的传输路径，左胸—右胸链路传输链路为直线路径，而左胸—腰部链路，则包含多种路径叠加，双耳链路还会存在空气链路叠加，图2、图3为跑步动作得到的左胸—右胸链路及左胸—右腰链路的归一化S参数曲线。

图2、图3所示4个动作为图中前4个奔跑动作的归一化S参数特性曲线，动作模型中手臂活动程度不同，5条链路表现出相似的波动特性。动作1相较于其它动作路径损耗最低，姿势为跑步中摆臂最大的动作。S参数在频率18MHz达到峰值。随着频率逐渐增加，信道衰减趋势减弱。曲线中信道曲线变化不超过3dB，表明在人体通信频段信道传输稳定，在人体活动及频率波动时传输信道没有明显波动。同一动作下右胸链路幅值高于右腰链路3dB左右，右胸链路在人体表面距离大于后者，表现出较高的路径损耗。4个连续动作中，手臂逐渐落下时路径损耗逐渐增大，手臂组织对于发射信号的反射与原直线路径信道信号进行叠加，使整体路径增益有所上升。

3 电磁与统计模型

为建立完整的数学模型，将人体连续行动中的仿真数据进行统计分析，将上述每一单独动作中的冲激响应幅值以及路径到达时间列出累计分布函数，采取最佳数学模型以描述特定参数的数学特性。对于路径增益上的变化，有可能成为概率分布模型候选方案，包括正态分布（Normal Distribution）、Log-Logistic分布、瑞利（Rayleigh）分布、威布尔（Weibull）分布等。通过MATLAB中的累积分布（CDF）拟合工具，选择最接近原曲线的几种数学模型，具体拟合参数结果见表1。

与文献[9]一样，为选出最佳分布函数，对于拟合数据采取经典的二阶赤池信息量准则（Akaike Information Criterion，AIC），对拟合结果按照从最好到最差顺序排序，通过AIC衡量统计模型优劣，以数据形式给出模型实际信息损失的相对度量如下：

AICc=-2loge（l（θdata））+2K+2K（K+1）（n-K-1） （3）

式（3）的第一项可通过数据的最大似然估计获得。最大似然估计反映模型对数据的整体拟合效果，模型越好AIC值越低。公式的后一项是用最少的参数对样本进行最优拟合。模型间的AIC值对比可反映出拟合优劣性，同时作为一种模型优于另一种模型的有力证据，采取如下两组公式以更清晰观察这种特性：

Δi=AICc，i-Min（AICc）     （4）

ωi=exp（-Δi2）Rr=1exp（-Δr2）        （5）

式（4）、式（5）中，Δ是每个拟合模型的AIC值，模型中的最佳拟合AIC值为0，AIC小于2时表明具备较好的拟合效果，ω为模型优劣性度量，是每个模型在所有模型中为最佳的概率。

表2为路径增益的几种拟合模型对比，AIC参数表明正态分布具有最佳拟合效果，图4为正态分布拟合效果。通过拟合得出功率增益幅值均值出现在90.83dB左右，功率增益遵循正态分布的物理意义也符合预期。电磁波在人体表面传播中，人体本身的反射及衍射效应可认为是一种乘性影响，所乘系数按统计变化的随机量[10]确定。

为建立统计模型，除了幅值拟合，还需对各路径到达时间进行拟合以构造模型。由于路径中每一径直线距离不同，路径到达时间自然不尽相同，但在整个信道中峰值路径的出现表现出统一的规律性。将一些可能成为概率分布模型候选方案的函数如正态分布、伽玛（Gamma）分布、逆高斯（Inverse Gaussian）分布、Rayleigh分布等考慮在内，具体拟合参数如表3所示。

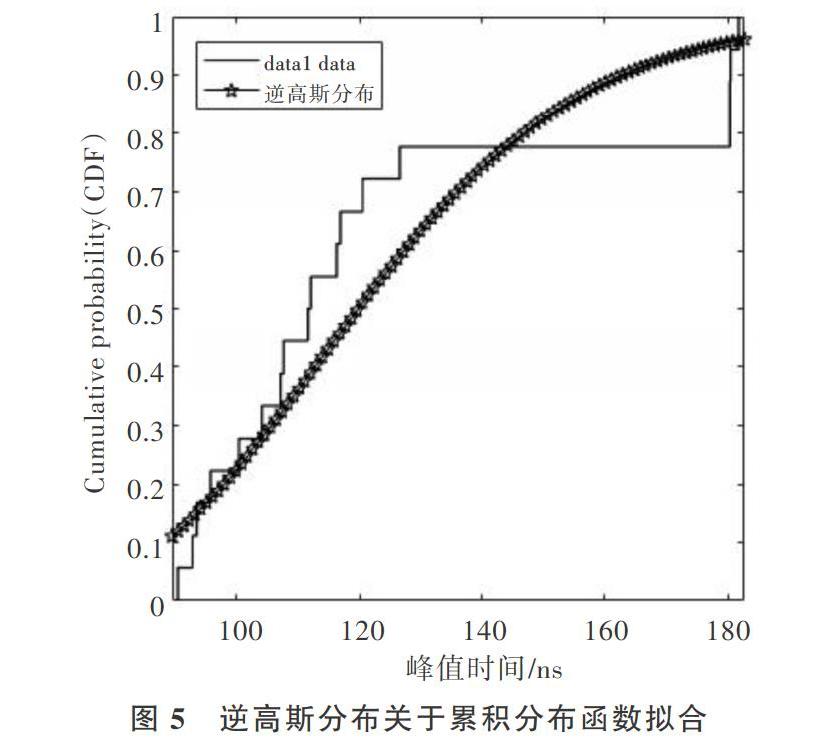
表4中，AIC参数进一步说明逆高斯分布具有最佳拟合效果，拟合峰值到达时间出现在123.278ns左右。图4中逆高斯分布标准差也是几种模型中的最小值，间接验证其是峰值到达时间最优拟合模型的结论。

传播链路在人体表面的距离约为0.5m左右，对于直线路径而言，第一路径到达时间在1.67ns左右，峰值拟合时间均值在123.278ns左右。由此可知，峰值出现是由于高频分量不断叠加的结果，包括发射极与接收极间的多径分量在不同幅值及相位上的相互叠加。实际应用中须对高频分量进行滤波处理，否则可能损坏人体通信设备。

4 结语

本文通过两步法得出人体奔跑动作的统计学特性。首先采用电磁仿真人体奔跑中连续的9个动作模型，随后通过统计学分析人体动作特性，得到人体活动统计模型。实验结果表明，人体简单动作会使信道稳定性波动在3dB以内，对信道稳定性不会产生明显影响。跑步动作中路径增益遵循正态分布，平均幅值约90.83dB，即信道在人体表面的衍射及反射效应是一种乘性影响，所乘系数为统计变化的随机量。逆高斯分布对于峰值路径出现时间具有最好的拟合效果，均值约在123.78ns左右，峰值为基频分量与高频分量叠加的结果，实际应用中须对此加以考虑。

参考文献：

[1] 韩世鹏， OLATUNJI， MUMINI， et al. 关于穿戴式人体传感器网络的研究思考 [J].  中国科学院院刊， 2017，16（12）：115-121.

[2] BAE J， CHO H， SONG K， et al. The signal transmission mechanism on the surface of human body for body channel communication[J].  IEEE Transactions on Microwave Theory & Techniques，2012，60（3）：582-593.

[3] ZHANG Q，SARRAZIN J，CASALETTI M，et al. Assessment of on-body skin-confined propagation for body area network[J].  IEEE Antennas and Wireless Propagation Letters，2017（9）：1-10.

[4] ZHU X Q，GUO Y X，WU W.  Investigation and modeling of capacitive human body communication[J].  IEEE Transactions on Biomedical Circuits and Systems， 2017， 11（2）：474-482.

[5] KANG T，OH K I，HWANG J H，et al. Measurement and analysis of electric signal transmission using human body as medium for WBAN applications[J].  IEEE Transactions on Instrumentation and Measurement， 2018（34）：1-11.

[6] ATTARD S，ZAMMIT S.  Effect of human movement on the body coupled communications channel in body area networks[C]. IEEE EUROCON， 2013：335-339.

[7] GIFIC.Dielectric properties of body tissues[EB/OL]. https：//www.fcc.gov/general/body-tissue-dielectric-parameters：niremf.ifac.cnr.it/tissprop/.

[8] WANG J， FUJIWARA T， KATO T， et al. Wearable ECG based on impulse radio type human body communication. [J].  IEEE Transactions on Biomedical Engineering， 2016， 63（9）：1887-1894.

[9] FORT A， DESSET C， DONCKER P D， et al. An ultra-wideband body area propagation channel model-from statistics to implementation[J].  IEEE Transactions on Microwave Theory & Techniques， 2006， 54（4）：1820-1826.

[10] WANG Q， TAYAMACHI T， KIMURA I， et al. An on-body channel model for UWB body area communications for various postures[J].  IEEE Transactions on Antennas & Propagation， 2009， 57（4）：991-998.

[11] XU R， ZHU H，YUAN J.  Electric-field intrabody communication channel modeling with finite-element method[J].  IEEE Transactions on Biomedical Engineering， 2011， 58（3）：705-712.

[12] KOSHIJI F，URUSHIDATE R，KOSHIJI K. Biomedical signal transmission using human body communication[C]. IEEE International Performance Computing & Communications Conference. IEEE Computer Society， 2017：1-2.

[13] 康雯， 鄭史烈， 章献民.  人体通信模型与信道特性研究[J].  微波学报， 2010， 26（4）：92-96.

[14] 夏萌， 曾以成， 聂泽东，等. 可穿戴设备中基于人体通信的身份识别方法研究[J].  计算机应用研究， 2017， 34（4）：1141-1144.

[15] 人体通信的信号传输机制与特性研究[J].  计算机工程， 2013， 39（8）：103-106.

[16] WANG J， NISHIKAWA Y， SHIBATA T. Analysis of on-body transmission mechanism and characteristic based on an electromagnetic field approach[J].  IEEE Transactions on Microwave Theory & Techniques， 2009， 57（10）：2464-2470.

[17] SHIMIZU Y，ANZAI D，CHAVEZ-SANTIAGO R，et al. Performance evaluation of an ultra-wideband transmit diversity in a living animal experiment[J].  IEEE Transactions on Microwave Theory and Techniques， 2017，874（52）：1-11.

[18] CHRIST A，DOUGLAS M G，ROMAN J M，et al. Evaluation of wireless resonant power transfer systems with human electromagnetic exposure limits[J].  IEEE Transactions on Electromagnetic Compatibility， 2013， 55（2）：265-274.

（责任编辑：杜能钢）