钢管混凝土组合框架抗连续倒塌鲁棒性初步分析
2022-11-07史艳莉王景玄
史艳莉, 王 雪, 王景玄
(兰州理工大学 土木工程学院, 甘肃 兰州 730050)
结构的鲁棒性是指在意外荷载作用下,结构不应产生与其原因不相称的垮塌,从而造成不可接受的重大人员伤亡和财产损失[1].英国结构安全常设委员会将结构鲁棒性定义为“抵御不成比例倒塌的能力”[2].目前,研究者们已经对结构的易损性进行了较多研究.黄冀卓等[3]通过计算各构件的重要性系数,得到结构的最不利初始损伤模型及构件的承载能力冗余度和稳定承载能力冗余度,最后取各冗余度指标的最小值作为结构的鲁棒性指标;罗文文等[4]分析了4种常用的倒塌判定准则判断结构倒塌的合理性,分析了各倒塌判定准则对确定RC框架结构抗倒塌能力的影响;施炜等[5]提出基于单自由度体系的多层钢筋混凝土框架倒塌易损性预测方法,计算量小且能够对多层钢筋混凝土框架的抗倒塌能力做出保守估计;于晓辉等[6]基于结构系统可靠度理论,提出了一种基于结构典型失效模式的地震侧向倒塌易损性分析方法;梁仁杰等[7]为研究结构抗横向倒塌能力,提出基于单自由度的等效模型,该方法计算过程简单且能够快速得到结构的抗倒塌强度;Li等[8]提出了一种评估钢筋混凝土框架结构抗连续倒塌能力的倒塌概率指标,基于该指标建立的易损性曲线可用来评价结构抗连续倒塌的冗余度;Li等[9]引入了一种新的基于承载力的指标来量化钢框架的鲁棒性,结果表明,对于柱失效引起的连续倒塌,减震对鲁棒性的影响大于材料应变率的影响;Weng等[10]提出了一种易于实施的针对钢筋混凝土框架的倒塌分析方法,试验表明,所提出的损伤评估标准对于RC框架的抗连续倒塌分析是有效和可靠的;Lin等[11]以六层钢筋混凝土框架为研究对象,通过易损性曲线分析两种设计的相互作用,分析结果表明,单独考虑不同危害的设计方法不适合于建筑结构的多重危害防治.
已有的易损性研究主要针对钢框架、钢筋混凝土框架展开,对钢管混凝凝土框架结构的易损性研究较少,本文借助有限元软件ABAQUS建立多层多跨钢管混凝土框架,利用两种基于构件重要性的方法分析各底层柱分别拆除后剩余结构的易损性,对比分析各底层柱对结构鲁棒性的影响.
1 构件重要性指标
1.1 基于承载力的构件重要性指标
杜永峰等[12]在黄靓等[13]提出的基于构件承载力的易损性系数的基础上,提出了简化后的构件易损性系数:
(1)
式中:φi为轴向荷载作用下构件i的易损性系数;Ni和Ni0分别为构件i的正截面所受轴力和正截面承载力.
由于
Ni=Aiσ,Ni0=Ai[σ]
(2)
可知
(3)
式中:σ为构件i正截面压应力;[σ]为材料容许压应力;Ai为构件i正截面面积.
由上式可知,0≤φi≤1,当φi=0时,表示构件i未承受任何荷载,易损性为0;当φi=1时,表示构件i达到了其极限承载力,若继续加载,则构件i失效.
构件重要性系数是评价构件易损性的基础,它体现了结构在受到外来荷载下各构件在抵抗荷载时的重要程度.
黄靓等[13]在文献[14]的基础上提出简化后的构件重要性系数:
γi=(R0-Ri)/R0=1-Ri/R0
(4)
式中:γi为失效构件的重要性系数;R0、Ri分别为原结构的极限承载力和构件i失效后剩余结构的极限承载力.
1.2 基于广义结构刚度的构件重要性指标
叶列平等[15]提出以构件失效后所引起的结构广义刚度损失比率I作为衡量构件重要性系数的指标,如式(5)所示:
(5)
式中:Kstru,0为原结构的广义结构刚度;Kstru,f为拆除构件后的广义结构刚度[16].
由广义结构刚度的定义式(5)可化简为式(6),即用结构的变形能表示的构件重要性评价指标:
(6)
式中:U′为拆除构件后结构的变形能,由于I的取值范围为[0,1],所以其物理意义为该构件对广义结构刚度的贡献.
2 构件鲁棒性系数
结构鲁棒性综合考虑构件易损性与构件重要性.基于该思想,杜永峰等[17]提出综合考虑外荷载和构件重要性影响的结构鲁棒性系数,但随着构件易损性与构件重要性的变化,结构鲁棒性系数变动过大,不利于比较分析.文献[17]中还提出了改进后的表达式:
(7)
式中:φi和γi分别是构件i的构件易损性系数和构件重要性系数;R为结构整体的鲁棒性系数.
由上式分析可知,结构鲁棒性系数随着易损性系数和构件重要性系数的减小而增大.
3 有限元模型的建立
3.1 模型设计
本文利用有限元软件ABAQUS分析了一个8层4×4跨钢管混凝土柱钢梁框架,层高3 m,钢梁尺寸为450 mm×300 mm×11 mm×18 mm,圆钢管混凝土柱核心区混凝土采用C40,钢管直径450 mm,厚度12 mm,外环板宽度100 mm,厚度20 mm,柱钢管及钢梁均采用Q345,混凝土密度2 400 kg/m3,钢材密度7 800 kg/m3.屋面与楼面恒载均为5.0 kN/m2,活载均为2.0 kN/m2,场地类别为Ⅱ类,地面粗糙度c类,抗震设防烈度为8度,设计基本加速度为0.2g,设计地震分组为第一组,抗震等级一级.结构标准层布置图如图1所示,图1中将角柱设为构件1,边柱设为构件2,中柱设为构件3,将构件1失效设为工况1,构件2失效设为工况2,构件3失效设为工况3.

图1 结构标准层布置图及失效柱位置
3.2 单元类型及边界条件
对钢管混凝土框架进行ABAQUS建模,如图2所示.针对钢管混凝土柱核心区混凝土,本文采用8结点六面体线性完全积分C3D8R单元,钢管和钢梁采用S4壳体单元.钢管与核心区混凝土采用面-面接触,节点处钢管与钢梁接触采用Tie(绑定)接触.
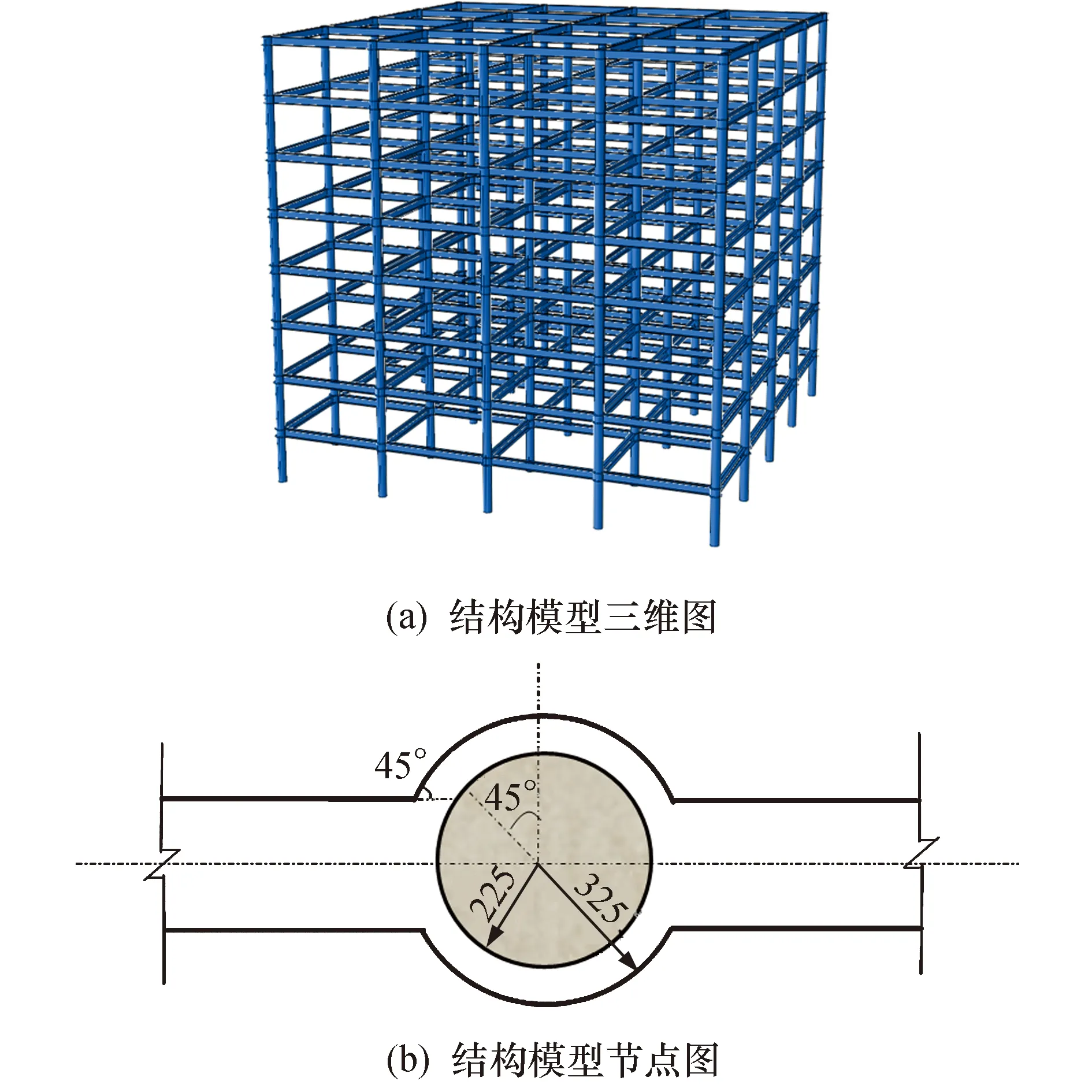
图2 结构模型三维视图及节点示意(mm)
边界条件的设定如下:为模拟柱端始终是固端约束,柱端采用U1=U2=U3=0;考虑失效柱时,采用杀死单元(model change)方法将失效柱移除.考虑失效柱时,在未失效柱柱顶采用线性加载方式施加竖向位移.
3.3 材料的本构关系
核心区混凝土的本构采用文献[18]中提到的核心区混凝土本构关系,表达式见式(8):
(8)

钢材的本构模型采用Esmaeily提出的钢材受拉、受压骨架线模型[19],如下式:
(9)
式中:Es为钢材的弹性模量;fy为钢材的屈服强度;εy为屈服应变;k1表示钢材强化段的起点应变与其屈服应变的比值;k2表示钢材的峰值应变与屈服应变的比值;k3表示钢材的峰值应力与屈服强度的比值.
4 计算结果与分析
4.1 基于承载力的鲁棒性分析方法
4.1.1构件易损性系数
本文将每层楼板所受面荷载转化为各层梁上的线荷载,荷载组合根据GSA中规定的F0=2(FD+0.25FL),FD为恒荷载,FL为活荷载,2为考虑构件瞬时失效时的动力放大系数,GSA假设某竖向承重构件失效,其影响范围为该构件周围,所以只需在与被拆除构件上部相邻开间的梁上作用2(FD+0.25FL)的等效荷载即可.为研究荷载对结构鲁棒性的影响,在其它条件均相同的前提下,以0.9 N/m为增量对各层梁施加逐级递增荷载,即0.9、1.8、2.7、3.6、4.5 N/m共五个荷载等级,分别定义为L1、L2、L3、L4和L5,分级荷载的取值只需保证结构在弹性工作状态即可.根据规范[20]中钢管混凝土轴压构件的正截面承载力公式可得本文模型中钢管混凝土柱的正截面承载力为16.261 MN,由式(1)可计算出三个分析柱的易损性系数,如表1所示.

表1 易损性系数
由表1可以看出,构件的易损性系数随着荷载的增大而增大,而影响荷载的因素有内部和外部因素,所以结构所承受的外荷载越大,构件的易损性系数就越大,构件的安全性就随之降低;还可看出,角柱的易损性系数相较边柱和中柱较小,中柱的易损性系数较角柱和边柱较大,即在外荷载确定的情况下,角柱失效时结构发生倒塌的概率较大,中柱失效时结构发生倒塌的概率相对较小.
4.1.2构件重要性系数
对原结构及三种工况分别进行非线性静力分析,对各柱柱顶进行位移加载,得到结构失效时各底层柱的内力和,即为结构失效时的极限承载力,依据式(4)计算出三个分析柱的构件重要性系数,如表2所示.

表2 构件重要性系数
由表2可知,角柱的重要性系数最大,边柱次之,中柱最小,即角柱相对于结构安全较为重要,边柱次之.为分析其中原因,图3给出了原结构及各工况下结构整体及失效柱相邻钢梁的应力云图.
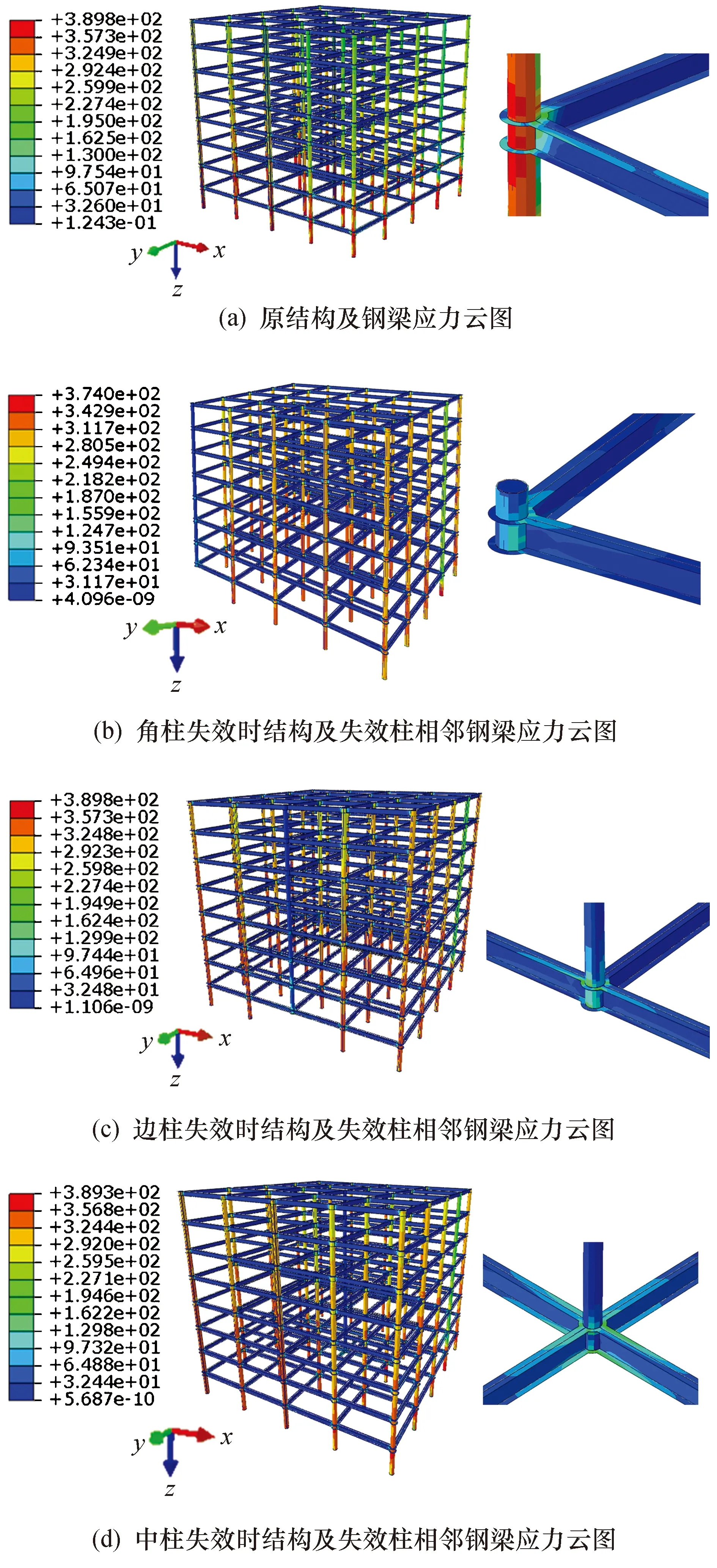
图3 各工况下结构及失效柱相邻钢梁应力云图(MPa)
由图3可以看出,当底层角柱失效时,与失效柱相邻的钢梁未达到屈服,钢梁发挥其梁机制作用,无法提供承载力较大的悬链线作用,所以仅有梁机制能够将上部荷载进行分散和传递,导致传递到相邻柱的荷载相对增大,容易引起相邻柱发生破坏,随着荷载增大最终导致结构发生连续倒塌,所以角柱相对于钢管混凝土框架较为重要;当边柱失效时,与失效柱相连的钢梁未达到屈服,失效柱节点处钢梁触发了单向悬链线机制,增大了该部分钢梁分散的上部荷载,所以边柱的重要性相对角柱较小;当中柱失效时,与失效柱相邻的钢梁均未达到屈服,容易得知,与之相连的钢梁可触发双向悬链线机制,钢梁分散的上部荷载明显增加,所以中柱相对于钢管混凝土框架的重要性相对较低.
4.2 基于广义结构刚度的鲁棒性分析方法
结构的弹性应变能是指结构在外荷载作用下由于发生变形而储存在结构内的能量,即结构变形越大,其应变能就相应提高.提取原结构及三个工况下结构的弹性应变能,如图4所示.

图4 各工况下结构的应变能
由式(6)计算出构件重要性系数如表3所示.

表3 构件重要性系数
由表3可以看出,工况1对应的结构应变能最大,工况3对应的结构应变能最小,也就是当角柱失效时,结构的变形相较工况2和工况3较大,当中柱失效时,结构的变形较小;与第一种方法所计算的构件重要性系数变化趋势相同,第二种方法计算出的构件重要性系数也是角柱最为重要,边柱次之,中柱的重要性相对较低.
4.3 结构鲁棒性系数
由式(7)可计算出两种构件重要性系数计算方法下结构鲁棒性系数,方法一为基于承载力的构件重要性系数计算方法,方法二为基于广义结构刚度的构件重要性系数计算方法,鲁棒性系数计算结果如表4.

表4 结构鲁棒性系数
结构鲁棒性系数越小,结构发生连续倒塌的概率就越大,由表4可以看出,两种方法计算出的结构鲁棒性系数变化规律相同,即结构的鲁棒性系数与外荷载呈负相关,也就是结构所承受的荷载越大,其发生倒塌的概率越大.所以,对于荷载确定的情况,可将构件重要性系数较大的构件进行加固或增加其传力路径,以此降低这些构件的重要性,可有效防止结构发生连续性倒塌.
4.4 双柱失效工况下结构鲁棒性分析
将构件1、2失效设定为工况4,构件1、3失效设定为工况5,构件2、3失效设定为工况6,在外荷载L1确定的前提下计算各工况下结构的极限承载力,进而得到结构的鲁棒性系数,如表5所示.

表5 结构鲁棒性系数
采用应变能的方法计算的构件重要性系数如表6所示.
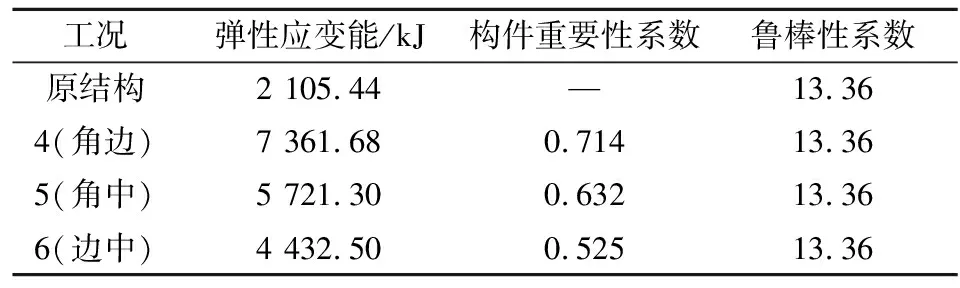
表6 构件重要性系数
由表5、表6可以看出,与单柱失效相比,双柱失效工况下失效构件的重要性系数明显较大,且结构鲁棒性系数明显减小,即双柱失效时结构发生倒塌的概率增大,符合常规认知;还可看出,工况4构件重要性系数最大,工况5次之,工况6最小,说明双柱失效时,双失效柱重要性由大到小排序为角柱和边柱、角柱和中柱、边柱和中柱,即角柱与边柱同时失效时,结构发生倒塌的概率最大,所以加固角柱和边柱,可有效降低结构发生倒塌的概率.
5 结论
1)钢管混凝土框架结构的鲁棒性系数取决于外部荷载的大小与构件重要性系数,结构的鲁棒性系数与外荷载的增加呈负相关,若外荷载确定,构件鲁棒性由构件重要性所决定.
2)两种计算构件重要性的方法计算结果相似,基于构件承载力的构件重要性系数计算方法物理意义较为清晰,而基于广义结构刚度的构件重要性系数计算过程较为简单.
3)对于钢管混凝土框架结构,角柱的重要性最大,边柱次之,中柱最小,实际中可采用备用荷载路径法对结构进行抗连续倒塌设计,即对重要性系数相对大的构件周围增加备用传力路径,以此防止结构在某一构件破坏的情况下发生连续性倒塌.
4)当双柱同时失效时,相较角、中柱失效和中、边柱失效,角柱和边柱同时失效会明显提高结构发生倒塌的概率.
