基于深度Q网络的飞行器增益调参技术研究

白文艳 张家铭 黄万伟 张 远,2

1.北京航天自动控制研究所，北京 100854 2.宇航智能控制技术国家级重点实验室，北京 100854

0 引言

高超声速飞行器(Hypersonic Vehicle)一般是指飞行马赫数大于5的飞行器。由于其飞行高度和马赫数跨度大、飞行环境复杂，气动和气热特性变化剧烈，使得飞行器存在非线性强和不确定性大的特点[1-2]。传统控制参数设计如增益预置法，是在选定特征点处对飞行器非线性模型进行小扰动线性化，随后根据调度变量进行插值，是一种成熟的控制方法，易于工程实现，方法简单，但是该方法需要大量的增益调节，还要满足变量慢变的假设，在非线性特性变化剧烈时性能较差。后来在增益预置法的基础上，发展了线性变参数(LPV)方法，该方法降低了调参工作量，并可保证较好的稳定性，具有工程实现性良好，设计相对简单的优点[3-6]。但是，随着飞行包线范围扩大，系统时变参数范围随之扩大，导致控制性能受到严重影响，难以满足动态特性变化下的姿态控制。针对上述问题，研究在复杂环境下高超声速飞行器的姿态控制参数自适应调节至关重要。

智能控制尤其是以强化学习、神经网络为主的控制方法是目前研究的热点之一。在航空航天控制领域，智能控制已逐渐成为未来发展方向[7-8]。强化学习(Reinforcement Learning)的特点是是智能体(Agent)与环境状态交互，通过不断试错的方式学习得到最优策略，使累计回报期望最大，这一过程称为马尔科夫决策过程(Markov Decision Process，MDP)[9]。国内外诸多学者研究应用强化学习于飞行器控制系统。文献[10]使用了强化学习算法设计了运载火箭姿态控制器参数；文献[11]针对再入飞行器姿态控制问题,应用单网络积分型强化学习(SNIRL)算法设计了姿态控制器。

本文提出采用基于深度 Q 网络(Deep Q network, DQN)的强化学习算法实现飞行器动静态增益自适应调节。利用强化学习与环境交互的优点，充分利用飞行状态等实时信息，在选定的特征点处，自动对控制增益调参，寻优效率更高。

1 问题描述

本文所研究对象为高超声速滑翔飞行器[12]，采用乘波体造型，尾舵采用正常式气动布局，颌下进气采取超燃冲压发动机。俯仰通道控制输入为升降舵偏δφ，输出为短周期模态下的攻角和俯仰角速率，其纵向运动模型为：

(1)

其中，V为飞行器的速度，θ为航迹角，ωz为俯仰角速率，α为攻角，H为飞行高度，x为飞行距离，m为飞行器的质量，g为重力加速度，Jz为飞行器绕弹体系z轴的转动惯量，T为发动机推力；L、D分别为飞行器所受升力和阻力，Mz为俯仰力矩，且有：

(2)

式中，CL、CD、Cm分别为升力系数、阻力系数和俯仰力矩系数，均为攻角、侧滑角、马赫数及俯仰舵偏的函数组合；ρ为该垂直高度下的大气密度，S为飞行器的横截面积，bA为飞行器平均气动弦长，S和bA可以认为是常数。

对高超声速飞行器纵向模型进行小扰动线性化后得到：

(3)

式中，a1、a2、α3、b1、b2均为动力学系数。

此时俯仰、偏航、滚转三通道之间的耦合作用影响较小，可以忽略，并考虑攻角作为输出量，不考虑各通道间的交连项，选取纵向短周期状态空间模型如下：

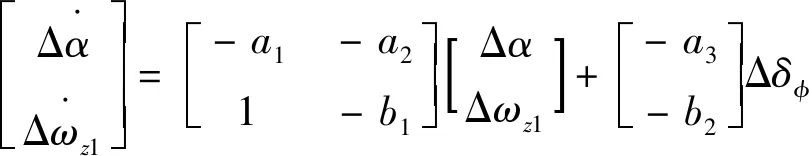
(4)

图1所示为俯仰通道姿态控制系统结构框图：

图1 俯仰通道姿态控制结构

其中，Wφ为校正网络传递函数，Wsf为空气舵伺服动态特性，kα和kω分别为攻角反馈系数和角速度反馈系数。

简化后俯仰通道控制方程为：

δφ=kαΔα+kωΔωz1

(5)

传统增益设计为人工离线调参，工程师依据经验在选定的弹道特征点处进行线性化并设计动静态增益，选取合适的调度变量形成插值表，缺点是线性化使模型产生误差，插值表也会造成特征点间的状态误差，且人工调试费时费力。

本文采取离散动作输出的强化学习算法——深度Q网络将飞行器作为智能体，与环境反馈并根据实时回报的机制调节增益。

2 基于深度 Q 网络算法的增益调参方法

2.1 深度 Q 网络算法原理

深度 Q 网络算法(Deep Q Network, DQN)是Q学习的升级，也是基于值函数的强化学习算法的典型代表，主要应用于无模型的离散动作控制的场景[13]。

首先介绍经典的Q学习算法，Q表是一张二维的表格，可以比较某个状态下不同动作的价值，用Q值表示，通过训练迭代更新，智能体选择最大的Q值代表最优策略。

Q表使用贝尔曼方程并采用两个输入：状态和动作，即可得到表中单元格的Q值：

Qπ(s,a)=E[rt+1+γrt+2+γ2rt+3+…|
st=s,at=a]

(6)

随后，进行 Q值更新：

Q(st,at)=(1-αQ)Q(st,at)+
αQ[rt+1+γmaxQ(st+1,at+1)]

(7)

其中，αQ为学习率，决定目标函数在合适的时间收敛到局部最小值；γ为折扣率，介于0～1之间，越接近1代表智能体更看重未来奖励;r为回报函数，即为执行动作后给予的奖励；Q(st,at)为当前时刻Q值，Q(st+1,at+1)为下一时刻Q值。

Q学习通过Q表的大小和形式决定了其只能应用于离散输出的场景，而且状态和动作空间不能过大，否则Q表面临数据量过大的问题。

DQN将 Q学习中 Q表更新的过程用神经网络拟合，解决了Q表维数限制。状态和动作作为神经网络的输入，Q值作为输出，通过神经网络计算当前状态和未来状态的Q值，不仅学习当前状态下的经验，也学习到了历史经验。即用一个函数Q(s,a,w)来表示Q(s,a)，即用深度神经网络进行拟合，其中w为函数的参数。

Q(s,a)=Q(s,a,w)

(8)

DQN中存在2个结构完全相同但是参数却不同的网络：Q估计网络和Q目标网络， Q估计网络使用的是最新的参数，而Q目标网络参数使用的却是很久之前的，Q(s,a,k)表示当前网络的输出，用来评估当前状态动作对的值函数；Q(s,a,k-1)表示目标网络的输出，因此当agent对环境采取动作a时，可以根据上述公式计算出Q，并根据LossFunction更新当前网络参数，每经过一定次数的迭代，就将当前网络的参数复制给目标网络。这样就完成了一次学习过程。

表1 给出了DQN算法的伪代码

2.2 马尔科夫决策模型设计

一个完整的马尔科夫决策过程包含(S,A,P,r,γ)，S为状态集合，A为动作集合，P为状态转移概率，r为回报函数，γ为折扣因子。

2.2.1 环境状态

环境状态S主要选取飞行状态量如高度、马赫、动压，攻角偏差量，俯仰角速度偏差量等信息，为了充分利用可观测的先验历史信息，提出多拍历史信息量作输入，更能体现出一段时间飞行器姿态控制的变化情况，从而映射到控制器参数的变化情况。选择控制周期为步长的5倍，即连续5拍的信息量作为环境状态集合∶

(9)

则环境状态空间为40维。

2.2.2 动作选择

姿态控制器的待调节参数向量为kp和kd2个调节参数。DQN算法为离散动作输出的形式，以一定的调整变化值增减这2个参数，调整步长为0.1。

2.2.3 回报函数-

强化学习通过试错来探索最优策略，获取最大奖励。

回报函数体现了智能体在训练过程中所选策略的效果，针对飞行器姿控系统，设计回报函数与状态偏差、控制量有关。

(10)

其中，x=[ΔαΔωz1]，u=δφ，Q为对称半正定矩阵，R为对称正定矩阵。

xTQx表征系统的控制效果，uTRu表征系统在控制过程中消耗的控制能量。

2.3 控制器设计

如图2所示，将2.2设计的马尔科夫模型加入到俯仰通道控制器中，根据DQN算法设计得到增益调参控制器。

图2 DQN境益调参流程图

综上，具体设计步骤如下∶

1)建立带有预设多种复杂非线性因素的飞行器姿态控制模型与姿态控制器结构;

选取N个平衡点。设飞行器姿态控制系统仿真试验运行时间为T。

2)针对每一次飞行器姿态控制仿真实验结果，设计交互学习的马尔科夫模型。

环境状态S"选取连续5拍状态数据及变化率，更好地体现一段时间内姿态控制参数随环境状态信息变化的情况。

姿态控制器共2个待调节参数，以0.1的步长调整2个参数的增减。

回报函数设置状态偏差为主要影响项，主要影响攻角偏差和俯仰角速率偏差。

3)根据每一次飞行器姿态控制仿真实验结果对应的交互学习环境状态、参数调整动作、回报函数以及历史学习经验 Q值更新学习经验 Q值;

学习经验Q值记为Q(s,a,k)，为环境状态s、参数调整行动a、第k次的飞行器姿态控制仿真实验时对应的学习经验Q值;在第k次的飞行器姿态控制仿真试验结束时，已知第k-1次仿真试验下所采取的参数调整动作为a(k-1)，所对应的环境状态为s(k-1)，学习经验Q值为Q(s,a,k-1);根据步骤2，获得第k次环境状态s(k)与第k次学习奖励r(k);更新学习经验Q值∶

Q(s,a,k)=(1-αQ)Q(s,a,k-1)+
αQ[r(k)+γmaxQ(st+1,at+1,k-1)]

(11)

4)利用每一次飞行器仿真实验后更新的学习经验 Q值，选择相应参数调节动作a，并获得优先行动集合∶

Ωa(k)={argmaxQ(s,a,k)}

(12)

argmax(f(x))是使得f(x)取得最大值所对应的变量点x(或x的集合)，即得到最大Q值所对应的参数调节下的控制增益。

5)根据步骤4)选择的参数调节动作，执行飞行器姿态控制仿真实验;若实验结果达成结束条件，则输出控制器参数，否则，跳转至步骤3，更新学习经验Q值。

3 训练及仿真结果分析

根据第2章内容进行智能体的训练，采取3隐层的BP神经网络，激活函数为Relu,其他具体训练参数配置如表2所示。

表2 训练参数配置

式(10)的累积回报经过1000次训练迭代，回报函数值逐渐增大。随着训练的进行，控制增益逐渐收敛；图3为随着神经网络的更新，训练集的拟合误差。可以看出误差范围收敛在0.04左右；图4所示第k次更新神经网络的训练误差值，具有线性递减趋势，表示随着神经网络的更新训练误差逐渐减小。

取回报函数值最大的一组控制增益，将其注入俯仰通道姿态控制系统，进行仿真验证，得到攻角及俯仰角速率的时域和频域特性曲线，其中式(4)中气动参数a1=0.5709，a2=-0.9638，α3=0.062，b1=0.9552，b2=9.0689

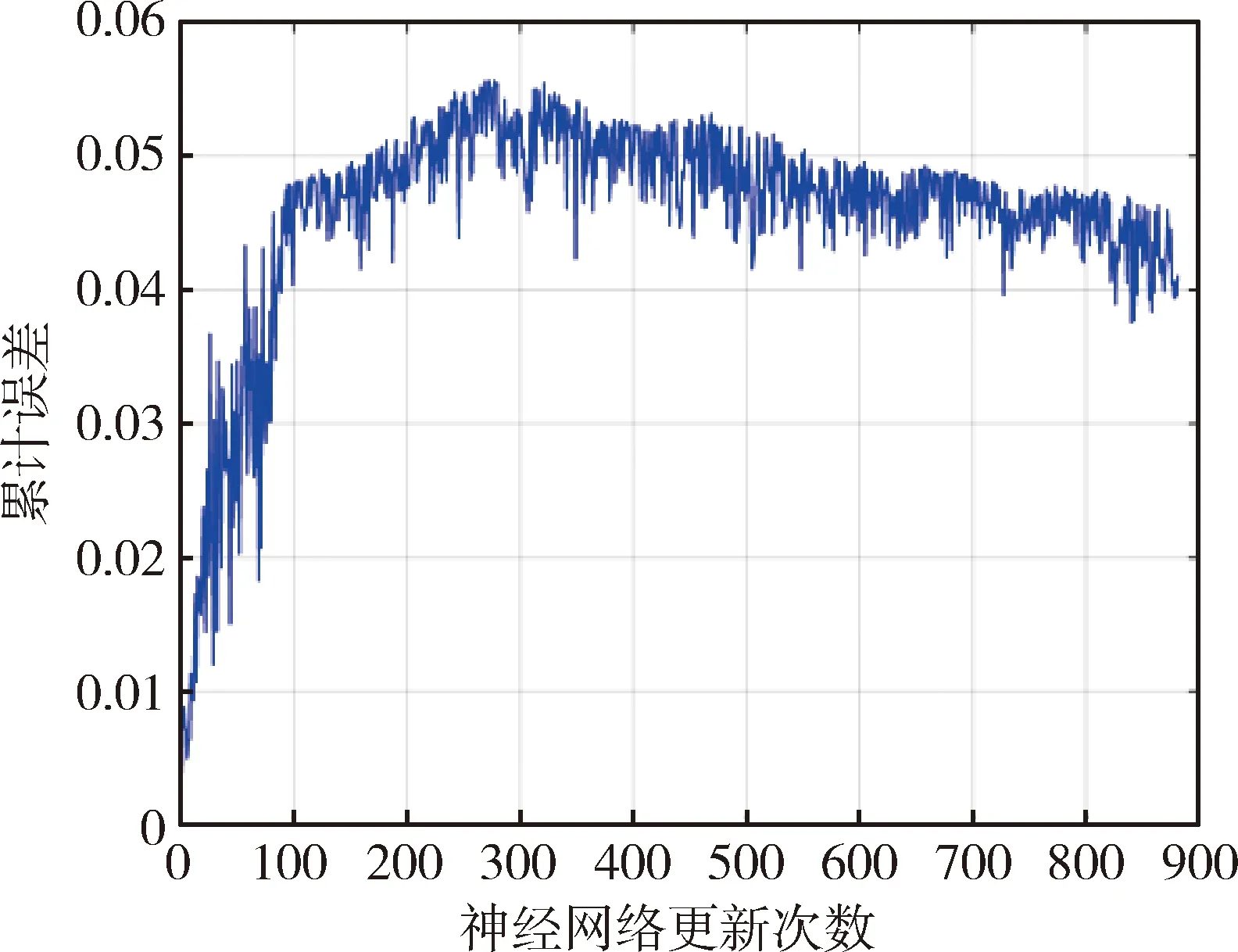
图3 训练集拟合误差

图4 第k次更新训练误差

图5 攻角响应曲线

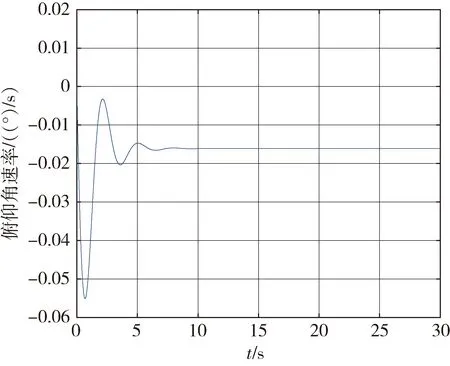
图6 俯仰角速率响应曲线

图5～6为采用强化学习训练的模型攻角及俯仰角速率的响应变化曲线、bode图。可以看出时域频域效果良好，经过强化学习训练后的增益使控制器在5s左右快速而平稳达到期望值，符合指标要求。

4 结论

采用深度Q网络的强化学习方法应用于飞行器俯仰通道姿态控制回路中，根据每一次飞行器姿态控制仿真实验结果对应的交互学习环境状态、参数调整动作、学习奖励以及历史学习经验Q值，更新学习经验Q值，选择参数调节动作，实现飞行器姿态控制增益自动调节。针对传统增益调度的缺点，强化学习算法能够有效减小人工经验调参产生的偏差，获得了良好的稳态和动态性能，具有一定的工程意义。