基座对弹道落点偏差影响机理研究

金 斌

中国人民解放军92981部队，北京 100161

0 引言

近年来，我国航天事业飞速发展，滑模控制[1]、机器学习[2-3]，智能规划[4-5]等领域不断取得突破，飞行器的综合性能也不断提升。精度[6]是评估飞行器性能的重要技术指标，在飞行器方案设计、试验、定型和使用等阶段都具有重要价值。导弹等弹道式飞行器落点精度分析的关键是制导系统设计的重要环节，包括影响落点偏差的误差源分析、落点偏差计算和精度指标分配等[7]。

对于采用惯性制导的弹道式飞行器而言，导致落点偏差的主要因素是初始定位定向误差和工具误差。目前，这两类误差源已得到学者们的关注和较为深入的研究：文献[8]考虑几何项、初值项和引力项，得到定位定向误差影响分析的完整解析解，并利用主动段状态空间摄动方程推导了定位定向误差的线性化传播模型。文献[9]提出了通过标准弹道估算定位定向误差对显式制导精度影响的解析方法。文献[10]提出了基于试验数据的潜射飞行器初始定位定向误差折合模型和基于模拟打靶的落点偏差折合方法。文献[11]提出了利用遗传算法确定最佳主成分子集的方法，工具误差分离结果的预测能力增强。文献[12]针对制导工具误差分离的线性模型，提出了基于稀疏约束的正则化模型。文献[13]针对海基动基座问题提出了试验数据、误差模型和弹道仿真相结合的精度分析样本生成方法。除此之外，方法误差和发射基座的运动状态等因素也对弹道式飞行器落点偏差产生影响。其中方法误差与计算机字长、数值计算方法、关机延时误差等密切相关，随着计算机硬件的发展和制导、计算方法的改进，方法误差对落点偏差的影响已得到了较好的控制。动基座发射平台发射弹道式飞行器时带来牵连运动，这种运动具有多自由度的特点，比如舰艇等动基座发射平台的运动具有6个自由度，即3个方向的摇摆运动和3个方向的线运动[14]。且相对而言，摇摆运动具有较大的随机性，飞行器起飞前就具备了此种牵连运动，由此引起飞行器出水时刻的运动状态必然会影响飞行器的落点偏差，目前对于该因素导致的落点偏差业内鲜有研究，本文将对此问题从误差影响机理和计算分析等方面进行研究与探讨，以期为该问题的研究提供参考与支撑。

针对以上研究的不足，提出了一种基于数学解析的弹道落点偏差分析方法，采用理论分析与计算推导相结合的方法，分别研究了基座水平速度、升沉速度、纵摇、横摇和偏航摇对落点偏差的影响，并通过算例分析的方式，分析不同误差因素对落点偏差的影响程度。主要工作如下：

1)分析了弹道落点偏差的产生机理，研究了基座水平速度、升沉速度、纵摇、横摇和偏航摇对落点偏差的影响；

2)建立了基座运动状态对飞行器落点的误差传播计算模型；

3)通过仿真试验验证了基于数学解析的弹道落点偏差分析方法的有效性，并分析了不同误差因素对落点误差的影响程度，为实际应用中减小落点偏差、提高基座性能提供了指导意见。

1 舰艇误差对落点偏差的影响原理

舰艇初始速度误差使得弹上制导计算的初值存在偏差，导致制导时采用的真速度与实际不符，从而影响导弹的制导、姿控和关机时间，进而造成落点的偏差。

1.1 坐标系定义及转换

为了描述舰艇的运动，定义艇体坐标系os-xsyszs，下面给出艇体坐标系与其它坐标系的关系。

1)艇体坐标系与北天东大地坐标系的变换

艇体坐标系os-xsyszs与北天东大地坐标系os-NRE之间的转换矩阵为：

Ns=M2(As)M3(-φs)M1(-γs)

(1)

其中，As为航向角，从当地北开始度量，顺时针为正；φs为俯仰角，向上为正；γs为滚动角，沿艇体轴向顺时针为正。

2)北天东坐标系与发射(惯性)坐标系的变换

发射瞬时，北天东坐标系os-NRE到发射(惯性)坐标系oa-xayaza之间的转换矩阵为：

Gs=M2(-AT)

(2)

其中，AT为发射方位角。

1.2 舰艇测速误差影响的分析方法

设舰艇惯导测得在艇体坐标系内的速度为Vs=(Vsx,Vsy,Vsz)T，转换到发射惯性系为：

VAs=M2(As-AT)M3(-φs)M1(-γs)Vs

(3)

VAs作为制导计算的速度初值偏差量，进行落点偏差影响分析时可利用偏导数法或弹道求差法[15]计算。

2 落点偏差机理分析

根据动基座运动的特点，可将基座运动3个方向的线运动和3个方向的摇摆运动分为水平面内的运动(水平速度)、垂直方向的运动(升沉速度)、纵摇、横摇、偏航摇5个分运动。

2.1 水平速度测量误差引起的落点偏差

动基座发射时飞行器具有和基座一致的水平运动，而动基座发射平台的水平速度通常由惯性导航系统给出，因此，可以通过坐标变换将该速度传递给飞行器制导系统，引入导航参数的计算。由于惯性导航系统测定的速度与动基座发射平台相对大地实际速度之间存在差异，因此，水平速度误差将引起飞行器的落点偏差。

弹道式飞行器(一般采用火箭助推)落点的纵向偏差ΔL和横向偏差ΔH可表示为[15]：

(4)

式中,Vk和rk分别表示标准弹道关机点速度与位置矢量，ΔVk和Δrk分别表示关机点速度偏差与位置偏差，其中的偏导数可采用求差法进行计算。

动基座发射平台水平速度测量误差最终将导致飞行器关机点速度及位置的误差，根据动基座发射平台航向与发射坐标系的关系，结合式(4)，可得水平速度误差引起的落点纵向偏差ΔLhs和横向偏差ΔHhs：

(5)

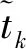
2.2 升沉速度引起的落点偏差

动基座发射平台的升沉速度难以精确操控，因此给飞行器制导带来误差，最终将导致飞行器关机点速度及位置的误差，结合式(4)，可得升沉速度误差引起的落点纵向偏差ΔLss：

(6)

式中，vss为动基座发射平台升沉速度，vky为发射系中关机点Y方向速度分量，yk为发射系中关机点Y方向位置分量。

2.3 纵摇引起的落点偏差

飞行器距离动基座发射平台摇摆中心的位置如图1所示，下标s、1分别表示动基座发射平台坐标系与飞行器体坐标系，发射坐标系则无下标。

图1 纵摇时飞行器位置关系

(7)

结合式(4)，可得纵摇引起的落点偏差ΔLzy：

(8)

2.4 横摇引起的飞行器落点偏差

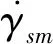
(9)

结合公式(4)，可得横摇引起的落点纵向偏差ΔLhy和横向偏差ΔHhy，如式(10)所示。

另一方面，动基座发射平台横摇角度将导致飞行器质心位置的变化，相对于飞行器数千公里的射程而言，这种变化可以忽略不计，但是过大的初始横摇角度将导致飞行器初始大姿态，易出现姿态失稳。

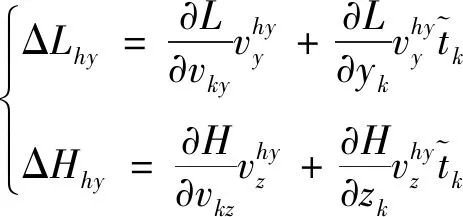
(10)

图2 横摇时飞行器位置关系

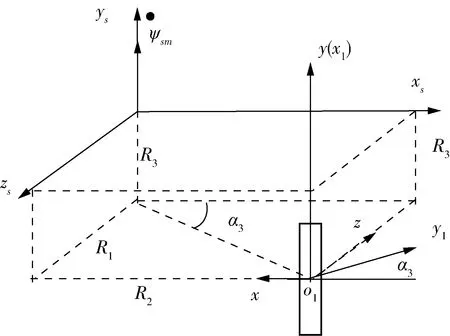
图3 偏航摇时飞行器位置关系

2.5 偏航摇引起的飞行器落点偏差

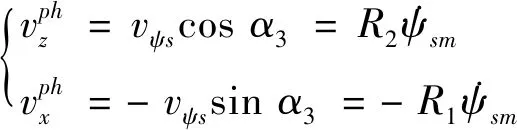
(11)

同理可得偏航摇引起的落点纵向偏差ΔLpy和横向偏差ΔHpy：

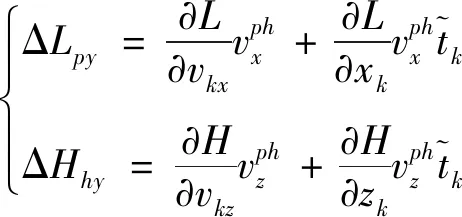
(12)

显然，动基座发射平台偏航角度将导致飞行器质心位置的变化，相对于大射程而言，这种变化可以忽略不计；但是过大的偏航角度将影响弹上惯性平台初始对准精度，限于篇幅，本文不对这一问题展开研究。

3 计算分析

3.1 算例

为分析动基座发射平台对飞行器落点偏差的影响，以某火箭为算例，相关参数如表1所示。

动基座发射平台的相关参数设置如表2所示。

由式(4)～(12)，结合上述给定的相关参数，计算结果如表3。

3.2 分析

由上述算例可以看出：

1)发射时动基座发射平台水平速度测量误差对于飞行器落点纵向和横向偏差均有影响，且对纵向偏差的影响尤为明显：这主要是由于弹道飞行器关机点射程导数∂L/∂vkx较大而导致的。

表1 算例火箭参数

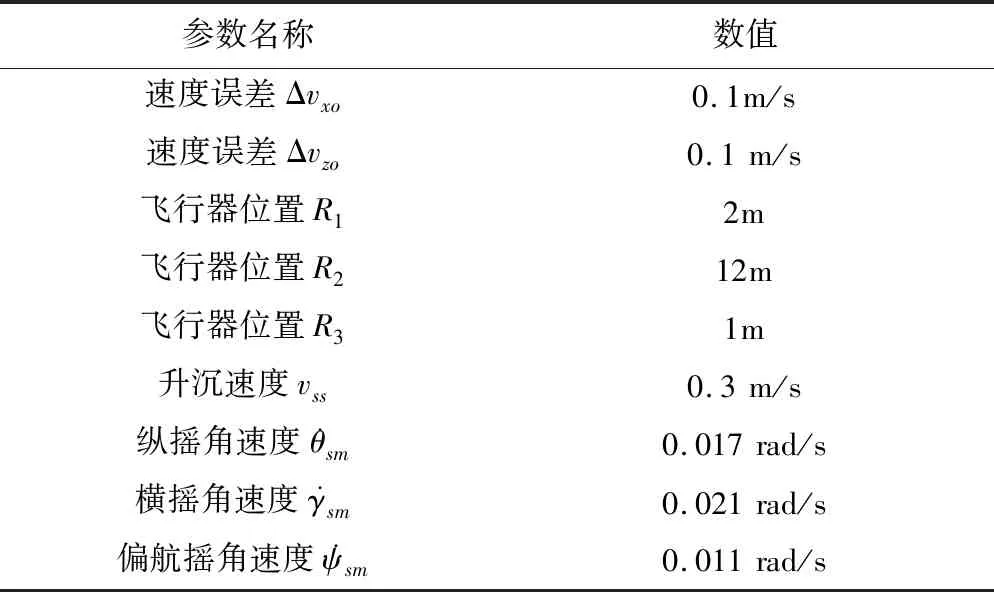
表2 算例动基座发射平台参数

表3 算例结果

2)发射时动基座发射平台的升沉和纵摇运动仅导致较大的纵向落点偏差。

3)发射时动基座发射平台的横摇和偏航摇均会导致飞行器落点纵向和横向偏差，但二者对于落点偏差的影响不如纵摇显著。

显然，为了提高飞行器的落点精度，应该提高动基座发射平台水平速度测量精度；同时，在飞行器飞行制导中对动基座发射平台水平速度、升沉速度、纵摇、横摇及偏航摇进行补偿。具体的补偿计算方法则可参考本文所述原理。

4 结论

受气流、洋流等现场环境因素影响，舰艇、飞机等动基座发射平台的运动属于典型的六自由度范畴，探讨动基座发射平台运动对于弹道式飞行器落点偏差的影响是提高精度的重要环节。本文从动基座发射平台平移运动和摇摆运动2个方面，基于弹道式飞行器落点偏差产生的物理与数学原理，通过理论分析与推导，分别研究了动基座发射平台水平速度、升沉速度、纵摇、横摇和偏航摇对于飞行器落点偏差的传播机理，建立了计算模型。并在此研究基础上，通过算例分析了上述几种因素对于飞行器落点偏差的影响程度，给出了提高落点精度的相应建议与方法。