大道至简 返朴归真——2022年新高考数学I卷第22题试题分析

广东省广州市第二中学(510000) 黄广兵

1 试题的基本描述

题目(2022年新高考I卷第22 题)已知函数f(x)=ex-ax和g(x)=ax-lnx有相同的最小值.

(1)求a;

(2)证明: 存在直线y=b, 其与两条曲线y=f(x)和y=g(x)共有三个不同的交点,并且从左到右的三个交点的横坐标成等差数列.

本题考查的知识点主要有导数、极值、最值、零点存在性定理,试题简洁明了,由几个常见的问题综合起来,要求学生有序地、分层次地解决即可得到最后的结果,有别于往年令人眼花缭乱的证明不等式或求参数范围问题.充分体现了“高考命题已经从能力立意转变为价值引领,素养导向,能力为重,知识为基”[2].事实上,本题是非常通透的,恰如其分地考查了学生直观感知,但最后的落脚点必须是理性证明.“通过考生的答题过程判断考生是否真正理解数学概念、是否真正掌握数学思维方法”[3].

2 答题情况

2.1 主要解法归纳

同理,可得x0是函数g(x)-b在(0,1)的唯一零点.ex0是函数g(x)-b在(1,+∞)的唯一零点,因此直线y=b与两条曲线y=f(x)和y=g(x)从左到右共有三个不同的交点(lnx0,b),(x0,b),(ex0,b),因为ex0+lnx0=2x0,所以这三个交点的横坐标成等差数列.

第(2)问解法2 由(1)知,当x趋于无穷时,f(x),g(x)均趋于正无穷.并且f(x)=ex-x在(-∞,0)上严格单调递减,在(0,+∞)上严格单调递增,g(x)=x-lnx在(0,1)上严格单调递减,在(1,+∞)上严格单调递增,从而y=b与它们最多有4 个交点.若b≤1 时,y=b与两条曲线y=f(x)及y=g(x)至多有两个公共点,不合题意,从而b ＞1.此时且f(x)在(0,1)上严格单调递增,g(x)在(0,1)上严格单调递减,因此y=f(x)与y=g(x)在(0,1)上有唯一交点,即存在x0∈(0,1), 使得f(x0)=g(x0), 取b=f(x0)=g(x0),满足题意,即

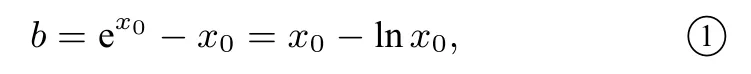
使得直线y=b与曲线y=f(x)及y=g(x)共有三个公共点,其横坐标从小到大记为x1,x0,x2,则x1＜0＜x0＜1＜x2, 满足f(x1)=f(x0)=g(x0)=g(x2)=b, 注意到f(lnx)=g(x), 所以有f(x1)=g(x0)=f(lnx0), 而由x1＜0,lnx0＜0,f(x)在(-∞,0)上单调递减知

同理可得

因此由①②③得x1+x2=lnx0+ex0=2x0,所以存在直线y=b,其与两条曲线y=f(x)和y=g(x)共有三个不同的交点,并且从左到右的三个交点的横坐标成等差数列.

2.2 典型错误

第(1)问典型错误及所占比例

1.规范性不足(所占比例: 9.60%)

求函数最小值时, 缺少单调性的论述.如: 直接令f′(x)=0 得x=lna, 接着默认f(x)的最小值为f(x)min=f(lna).而论述单调区间时候, 部分考生并没有把x的范围求出来.如: 当a ＜ex时,f(x)在(-∞,ex)单调递减.

2.极值与极值点的概念混淆(所占比例: 5.67%)

3.论证不够严密(所占比例: 14.00%)

由方程a-alna=1+lna,直接得到a=1,缺乏对方程解的唯一性的论述.

4.不会解指数方程(所占比例: 4.93%)

令f′(x)=ex-a=0 得x=x1,后续运算带着x1,最终无法解决问题.

5.逻辑错误(所占比例: 3.67%)

令a=1,直接展开做题.

6.缺乏分类意识,直接默认a ＞0 展开解题(所占比例:92.6%)

第(2)问典型错误及所占比例

1.依赖几何直观,缺乏代数运算(所占比例: 48.39%)

学生直观得到f(x)与g(x)有交点x0,缺乏对x0的存在性和唯一性的严格论证.

2.缺乏解题目标, 做无用的代数变形(所占比例:28.23%)

由b=ex1-x1=ex0-x0=x0-lnx0=x2-lnx2,反复移项最后得到x1+x2=2x0.事实上,若没有x1=lnx0,x2=ex0则无法推出结论,即学生省略了不可或缺的推理步骤.

3.逻辑欠严密(所占比例: 29.23%)

由f(x1)=f(lnx0)直接得到x1=lnx0,缺乏对f(x)的单调性进行论述或讨论方程f(x)=b解的情况.

2.3 得分情况

得分分布表

由上表得分及对应比例可以看出此题入口宽,但是难以准确论证,对于良好和中等的学生区分度不明显.

3 题源及变式

本题主要是源于互为反函数的函数图像关于直线y=x对称.水平直线y=b与f(x)=ex-x,g(x)=x-lnx的图像有四个交点A,B,C,D,如图1 所示.

图1

从而有b=ex-x,b=x-lnx,即ex=x+b,lnx=x-b,转化为如下情形,如图2 所示,直线y=x+b与f(x)=ex图像交 于 点A(x1,ex1)、C(x3,ex3), 直线y=x - b与g(x)=lnx图像交于点B(x2,lnx2)、D(x4,lnx4).因为A、B两点关于直线y=x对称, 所以x1=lnx2, 因为C、D两点关于直线y=x对称, 所以x4=ex3, 从而x1+x4=lnx2+ex3=x2-b+x3+b=x2+x3.

图2

基于此原理,可以命制如下的变式题:

变式一已知函数f(x)=ex -x,g(x)=x-lnx,证明: 存在直线y=b, 其与两条曲线y=f(x)和y=g(x)共有四个不同的交点, 从左到右的四个交点的横坐标分别为x1,x2,x3,x4,且x1+x4=x2+x3.(若x2=x3,即成为2022年新高考I卷第22 题.)

考虑运行策略和投资主体利益的电转气容量双层优化配置//许志恒,张勇军,陈泽兴,林晓明,陈伯达//(13):76

注意到y=x+b与y=x-b也互为反函数,进一步理解这类问题是由两组互为反函数的函数来命制的,于是把直线方程替换为与y=bx,考虑如下情形:

图3

则x2,x4是关于x的方程lnx=bx的两根, 因为A、B两点关于直线y=x对称, 所以x1=lnx2, 因为C、D两点关于直线y=x对称, 所以x4=ex3, 从而x1x4=(lnx2)(ex3)=(bx2)

基于此原理,可以命制如下的变式:

变式二已知函数,证明: 存在直线y=b,其与两条曲线y=f(x)和y=g(x)共有四个不同的交点,从左到右的四个交点的横坐标为x1,x2,x3,x4,且x1x4=x2x3.

4 教学及备考建议

首先,教师在日常教学和备考中要主动理解试题的内容属性,明确考查目标中的必备知识、关键能力、学科素养以及核心价值[4].因为在国家教育题库2.0 的支撑下,两个创新研究尤其突出: 高考命题从任务导向到过程导向的新管理模式创新; 围绕题库系统梳理考试全流程的数据生态体系创新.重塑考试业态,并在大数据和信息技术辅助下,形成命题相关的新工作和分析方法[5].从这个角度看2022年新高考I卷第22 题就有豁然开朗的感觉.此压轴题非常平实,又清新脱俗,焕发一种不同以往的风格.第一问是常规的求最小值问题,且所给函数也非常简洁,考查了必备知识.不过也设置了一点梯度,需要学生直观探索超越方程a-alna=1+lna的根,然后再构造函数来说明根的唯一性,考查了关键能力.第二问证明f(x),g(x)两者图像有唯一交点,也需要构造函数,根据零点的存在性定理来说明,突出了学科素养.客观来说,在六道解答题中,此题难度并非最大,为何处于最后压轴位置? 众所周知,现在各种解题模式泛滥,甚至高一高二的教学都脱离课本最基本的定义和定理,教学和解题都异化为套路,学生得其形而不得其神,与国家的育人选材理念背道而驰.这道压轴题无疑是一种重要的价值导向: 数学要重视回归到的最基本的演绎说理.

其次,“现在没有,将来也不会有任何事情具有像数学这样的体系结构......,尽管教师可能依赖所教数学能直接被应用的程度往数学中掺杂更多东西,仍存在着一种倾向: 把数学作为一种特别的体系结构来教授”[6].我们高三教学更要注重帮助学生形成各种小的或大的结构,有利于学生更好地存取知识并能快速同化所遇到的问题.例如“利用导数研究函数的性质”这个结构应该至少包含如下线索:

(1)利用导数研究函数的性质的核心问题是研究方程f′(x)=0 的实根的情况;

(2)如果方程f′(x)=0 无实根,那么函数f(x)单调;如果方程f′(x)=0 有实根,则进入“求根”环节;

(3)如果方程f′(x)=0 的实根可以通过因式分解或者求根公式得到,那就可以进一步分析单调性、极值、最值;

(4)如果方程f′(x)=0 的实根不可以通过因式分解或者求根公式得到, 但是可以通过观察、猜测得到, 那就进一步求f(x)的二阶导数, 据此判断所观察、猜测的方程f′(x)=0 的实根是否唯一,然后进一步分析单调性、极值、最值;

(5)如果方程f′(x)=0 的实根既不可以通过因式分解或者求根公式得到,也不可以通过观察、猜测得到,那可以先把方程f′(x)=0 是否有实根转化为两个函数图像是否有交点直观感知,例如对于函数

再次,注重学生表述的准确性和教师教学规范性.学生表述的准确性是其关键能力和学科素养的外显,在阅卷过程中,评卷员在评分细则指导下,有可能会对某些表述的准确性进行模糊化处理,从而在分数的角度无法体现出来,实际上这还有很大的提升空间.从学生答题情况来看,我们日常教学中,教师面对不同的生源,在函数与导数的教学中要求的尺度差异非常大,为了教学上的简便,简化甚至删减了部分内容,尽管这可以理解为分层教学,然而“教师或其他人对学生的能力认识是造成学生数学成绩水平差异的主要原因”[7],对于含有一个参数的简单的函数,最基本的求导,分析单调性,求极值和最值,绝大部分学生都应该掌握,这都有基本的教学规范.除此之外,适当的纵深教学是必须的,繁难内容通过精心组织,合理呈现,完全可以提高学生的吸收和转化水平.事实上,中学数学教育最重要的一个任务是保持学生对数学的兴趣和热情,这必须源于对数学的深刻理解并有一种恍然大悟的喜悦和成就感, 而且知识之间具有隐性关联,教师人为剔除或者弱化某些知识难点, 这种不规范的做法,获得了教学上的便利,却付出了学生不及预期的代价.

5 结语

细细品味2022年新高考数学I卷,既在意料之外,又在情理之中,而第22 题那种静水流深的感觉反衬了聒噪的教学和备考百态.尽管资源日益丰富,教研更加繁荣,关于高考备考的各种思考和追求,归根结底还是要回归到日常的、平实的、有理解深度的教学中,我们必须保持勤奋、谦虚、好学和时代的敏感性,与国家、社会共同进步.