2022年新高考I卷第17题的探究与教学启示

广东省佛山市乐从中学(528315) 林国红

一、题目呈现

二、解法探究

2.1 问题(1)的解答

把上述式子相乘,得

把上述式子相乘,得

2.2 问题(2)的解答

评注①问题(1)实际上是对数列的前n项和Sn与通项an的关系式的考查,这是数列的常见且重要题型,4 种解法借助a1=S1,an=Sn -Sn-1(n ＞1)从不同的角度进行转化,再利用累乘法或构造法解答.

②问题(2)考查裂项相消法求和, 属于数列求和的常见、简单的内容.

③解法3 与解法4 还可以构造常数列的方法进行解答.以解法3 为例: 因为, 所以数列是首项为的常数列, 则

三、试题的推广

经探究,上文的高考题可推广如下:

评注显然在推广试题中,当k=3 时,就是高考题的情形.

四、试题的命题背景与拓展

4.1 试题的命题背景

从上述推导过程,发现数列{an}的前n项和Sn隐含着杨辉三角的一个美妙且重要的性质:

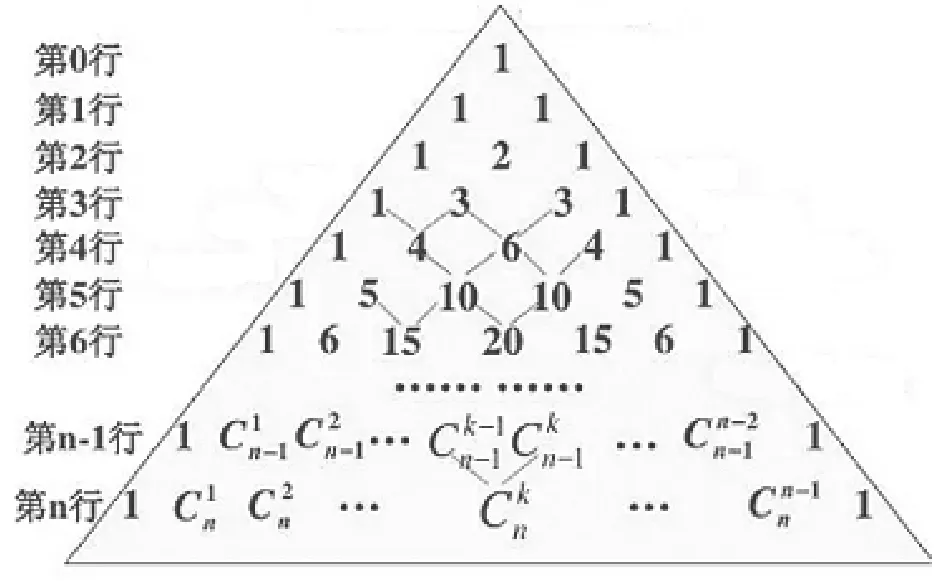
在杨辉三角中(如图),从第二行起,每个数字等于上一行的左右两个数字之和,也就是第n+1 行的第i个数等于第n行的第i-1 个数与第i个数之和,即Cin+1=Cin+Ci-1n.这个性质是杨辉三角的最基本性质(也是二项式系数和组合数的性质),用此性质可以写出整个杨辉三角,它也是研究杨辉三角其他性质的基础.

可见,杨辉三角的有关性质与组合数的性质正是试题的命题背景.

4.2 试题的拓展

由上述性质,可以命制相关的题目.例如:

拓展试题2记Sn是数列{an}的前n项和, 已知是公差为的等差数列.

(1)求数列{an}的通项公式;

五、试题的变式

数学的魅力在于“变化”,有“变”才能“活”.恰当的“变式”能使学生多角度、全方位地理解知识,思维能力得到拓宽和加强,会起到强化解题思想方法的积极作用.所以数学教学不仅要解决问题,还要注重问题的变式拓展,引导学生积极探索一题多变、一题多用,达到了举一反三,触类旁通的目的.对于本题,可以进行如下变式训练:

变式1已知正项数列{an}的前n项和Sn满足:Sn=2an-2,(n ∈N+).

(1)求数列{an}的通项公式;

六、教学启示

1.教学应以课程标准为基准,夯实基础

高考对数列内容的考查,虽然试题千变万化,但都以基础知识、基本能力、基本思想、基本活动经验为基础.所以在教学中要以课程标准为轴,围绕教材,对重点内容强化复习,夯实基础知识.

2.认真研究考题,把握高考命题方向

把脉高考命题方向是每位教师在进行备考前的一项重要工作,从近几年高考对数列考查内容和方向来分析,变化不大,保持较高的稳定性.主要考查数列的基本概念,等差、等比数列相关概念和性质,通项公式,前n项和等方面的知识.

(1)掌握求数列通项公式的常用方法高考数列试题常以等差、等比数列的基础知识及综合运用为主.要会用“基本量思想”求解等差、等比数列的通项公式;能由特定的递推关系式求解通项公式(如累加法、累乘法等),并会通过“构造新数列”(如取倒数等)研究数列的通项公式;会用an与Sn的关系求通项公式.同时还应掌握一些基本方法(如因式分解、配方法等).

(2)掌握求数列前n 项和的常用方法要熟练掌握公式法、分组求和、错位相减、裂项相消、奇偶分析和并项求和等方法研究数列前n项和.在教学中要重视对公式方法的推导,并借助相应的练习巩固对方法的认知.

(3)做好近年高考题的归类整理备考选题以全国卷为主,分类分组训练,避免类型“盲区”,并领会题目所蕴含的数学思想与方法.

3.促成学生转化应用能力

近年数列试题的命制, 其考查内容离不开定义和性质,但考查的形式和角度不再单一,而呈多样化的趋势.有时把数列知识渗透在数学文化中,考查学生分析问题和解决问题的能力,以及理论联系实际能力;有时会给出新定义和新情景,要求考生在新定义和新情景中明晰数列知识的角色参与;有时会与其它内容交汇,考查数列知识的综合应用.这些试题的考查目的是促使学生理解好数列的本质内涵,熟悉数列知识的背景,灵活利用已知解决未知,实现知识间的相互转化.

(1)加强数学阅读理解能力的训练,提升数学抽象和教学建模素养高考试题信息量有变大趋势,需要学生能快速的在繁杂的信息中抽象出数量关系和建立模型.

(2)重视逻辑推理素养的达成解题教学是逻辑推理素养达成的主要途径之一,在教学中,要重视学生解题活动的高参与度,引导学生通过解题活动加强对基础知识的巩固与系统掌握,通过对条件与结论的分析,探索论证的思路,选择合适的论证方法,提升辑推理能力.

(3)精细化创设问题情境,提高学生的创新意识在教学中,要以现实生活为背景创设情境,为培养学生创新意识搭建平台,便于他们深入理解、诠释、反思、探究,更好地掌握数列的核心概念和数学思想方法, 提高学生的数学思维品质,促进创新能力的提升.