2022年北京高考导数题的多角度解析和学习建议

北京大学附属中学(100190) 桑胜景

首都师范大学附属中学(100048) 李 洋 姚 璐

一、原题解读

题目(2022年高考北京卷第20 题)己知函数f(x)=exln(1+x).

(I)求曲线y=f(x)在点(0,f(0))处的切线方程;

(II)设g(x)=f′(x),讨论函数g(x)在[0,+∞)上的单调性;

(III)证明: 对任意的s,t ∈(0,+∞), 有f(s+t)＞f(s)+f(t).

解读该题考查的函数为指数函数与对数型函数的乘积,不含参数.其中第一问求函数的图像(曲线)在给定点(在曲线上)处的切线方程,方法明确,过程简单,需要用到乘法求导和复合函数求导法则.第二问考查导数在给定区间内的单调性,需要在第一问求出导数的基础上,对导数再求导(即二次求导),同时判断二次导数的符号,据此得到结论,方法常规,但计算稍显复杂,判断二次导数正负需要观察其结构,具有一定技巧性.第三问在给定区间内证明含有双变量的不等式恒成立,常规的参变分离方法、消元方法难以处理.要求学生结合前两问在抓住原始函数性质的基础上,灵活运用相关知识解题,难度较大.

解(I)由题知所以f′(0)=1, 又因为f(0)=0, 所以曲线y=f(x)在点(0,f(0))处的切线方程为:y=x.

(II)结合(I)可得:

当x ∈[0,+∞)时,ex ＞0,ln(1+x)≥0,所以＞0,从而有g′(x)＞0,所以函数g(x)在[0,+∞)上的单调递增.

二、第三问多角度探究

解法1(主元法)令h(x)=f(x+t)- f(x)- f(t),x ∈[0,+∞)其中t为参数,t ∈(0,+∞), 则有h′(x)=f′(x+t)-f′(x).由(II)知,函数f′(x)=g(x)在[0,+∞)上单调递增,结合t ∈(0,+∞)可得x+t ＞x≥0,从而有h′(x)=f′(x+t)-f′(x)＞0,所以h(x)在[0,+∞)上单调递增,从而有当s ∈(0,+∞)时,

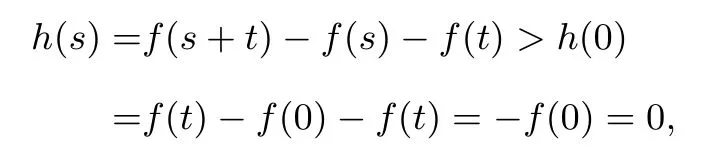
即有f(s+t)＞f(s)+f(t).

注该方法的本质是将待证不等式作差后固定双变量中的一者t,构造关于另一个变量s的函数,确定主元,将双变量问题转化为单变量问题进行研究.

解法2(根据自变量之差构造新函数)因为f(0)=0,所以f(s+t)＞f(s)+f(t)⇔f(s+t)-f(t)＞f(s)-f(0).令F(x)=f(s+x)-f(x),则有f(s+t)-f(t)＞f(s)-f(0)⇔F(t)＞F(0), 所以只需证明F(x)在[0,+∞)上单调递增.F′(x)=f′(s+x)- f′(x)=g(s+x)- g(x).因为对任意的x ＞0,s+x ＞ x ＞0, 所以由(II)可得g(s+x)＞ g(x), 所 以F′(x)＞0, 从 而F(x)在区间[0,+∞)上单调递增.所以对任意的t ＞0,F(t)＞F(0),即f(s+t)- f(t)＞f(s)- f(0)=f(s), 即对任意的s,t ∈(0,+∞),有f(s+t)＞f(s)+f(t).

注该方法与解法1 形式相像, 但其出发点不同.这里是利用f(0)=0, 将待证不等式进行变形, 使其左右两边变为同一个函数在不同自变量处的取值, 继而构造函数并利用其单调性证明.根据变形后不等式的不同, 该题还可以通过变形为f(s+t)+f(0)＞f(s)+f(t), 构造函数y=f(x)+f(s+t-x)并研究其单调性证明.

解法3(利用函数图像上的点与原点连线的斜率变化处理)令,x ∈(0,+∞),则有

注该方法主要是利用了函数在(0,+∞)上的单调性处理,此处用到了函数f(x)的具体形式,但实际上, 相关单调性还可以直接利用前两问的结论形式化证明,而不需要代入函数f(x)的表达式,具体如下:

令H(x)=xf′(x)-f(x),x ∈[0,+∞),则有H′(x)=xf′′(x)+f′(x)-f′(x)=xf′′(x)≥0,又因为等号不在任何区间内同时取到,所以函数H(x)在[0,+∞)上单调递增,所以当x ∈(0,+∞)时,H(x)＞H(0)=0,即有h′(x)＞0,从而有h(x)单调递增.

解法4(转化为平均变化率关系(拉格朗日中值定理))由拉格朗日中值定理可得,存在x1∈(0,t),x2∈(t,s+t)满足:

由(II)知,函数f′(x)=g(x)在[0,+∞)上的单调递增,所以f′(x2)＞f′(x1),从而有

结合f(0)=0 可得f(s+t)＞f(s)+f(t).

注解法3 和解法4 在本质上是一样的,都是用到了函数图像上两点连线的斜率变化规律,解法3 用的是中学数学的方法,可以在中学推广;解法4 用到了数学分析的内容,形式简单,感兴趣的同学可以了解.

解法5(定积分方法)由定积分定义可得:

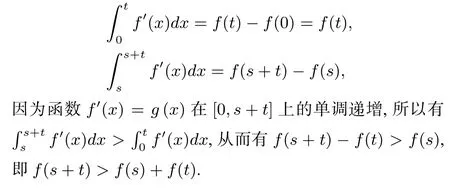
注解法4 和解法5 用到了高等数学的部分知识,其在本质上是一致的,都是通过建立导函数的单调性与原函数的联系来解题,不同之处在于解法5 用到的是一个区间内的性质,而解法4 是利用中值定理转化成对应两个导数值之间的大小关系比较.

解法6(结合下凸函数性质处理(超线性))

如图1,对于函数F(x),若其图像上任意两个不同点连线之间的线段(不含端点)都在函数图像的上方,则称F(x)为下凸函数(从图像上可以形象的理解下凸函数的图像是向下凸出的),仿照解法3 和解法4 的证明,很容易得到对于在某个区间二阶可导的非常值函数F(x),F(x)在该区间为下凸函数等价于F′′(x)≥0 在该区间恒成立(但不在任何区间内恒取等号).

图1

用符号语言表述下凸函数的性质即为: 对于在区间D内的下凸函数F(x),图像上的两个互异点x1,x2∈D有:F(λx1+(1-λ)x2)＜λF(x1)+(1-λ)F(x2), λ ∈(0,1).①在上式中取x1=s+t,x2=0 并依次取和便可得到下面两个的式子:

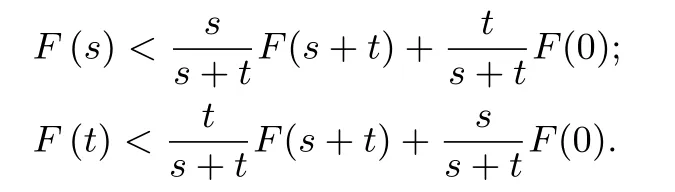
两式相加便有F(s)+F(t)＜F(s+t)+F(0),具体到原题中的函数f(x)便有f(s+t)＞f(s)+f(t)-f(0)=f(s)+f(t).

注如果对①式进行变形, 便可推出上凸函数的等价性质:F(λx1+(1-λ)x2)＞λF(x1)+(1-λ)F(x2),其中λ ∈(-∞,0)∪(1,+∞)且λx1+(1-λ)x2∈D.

上式从图像上理解便是函数图像上任意两点所连线段的延长线都在函数图像的下方,即函数F(x)在区间D上因变量和自变量满足超线性关系.另外关于函数在凹凸性视角下的研究可以查看文献[1].

解法7(二元函数处理(偏微分))令h(x,y)=f(x+y)- f(x)- f(y),x,y ∈[0,+∞), 结合第二问中函数g(x)=f′(x)的单调性可得:(x+y)-f′(y)≥0,且两个等号均不在任何开集内恒成立,进而有当s,t ∈(0,+∞)时h(s,t)＞h(0,0)=0,即有f(s+t)＞f(s)+f(t).

注解法7 与解法1 的方法类似,不同之处在于构造的函数一个是单变量的,一个是双变量的,相比之下解法7 的方法适用性更强,但需要大学知识的应用.

三、拓展

原题中虽然出现了两个变量s,t,但该题本质上是探索关于四个函数值f(s),f(t),f(s+t)以及f(0)的大小关系的问题.仿照前述证明,可以将原题的结论推广到一般的上凸函数和下凸函数得到以下拓展内容:

已知定义在区间D上的函数f(x)(如y=ex,y=x2等),以及a,b,c,d ∈D,且a ＜b ＜c ＜d,a+d=b+c.

拓展1若函数f(x)在区间D上为上凸函数, 则有f(a)+f(d)＜f(b)+f(c).

拓展2若函数f(x)在区间D上为下凸函数, 则有f(a)+f(d)＞f(b)+f(c).

四、学习建议

若将原题第三问改为以下表述: “证明: 对任意的a,x ∈(0,+∞), 有f(x+a)＞f(x)+f(a).”学生便较容易想到将x作为变量,a作为参数作差构造函数处理(类似于法1),其原因在于学生往往对题目中不同字母的身份有较为刻板的印象.这就要求在导数相关的学习中能从模式化的解题套路中跳出来,真正把导数当做工具,结合函数的图像和性质抓住问题的本质,更加灵活地处理相关问题,同时关注不同思考角度的出发点和思路分析、总结.