2022年全国乙卷理科导数题的解法探究与拓展

2022-11-03湖南省长沙市雷锋学校410217童继稀曾文乐

中学数学研究(广东) 2022年19期

关键词：切线零点个数

湖南省长沙市雷锋学校(410217)童继稀曾文乐

一、试题分析与反思

题目1(2022年高考全国乙卷理科第21 题)已知函数f(x)=ln(1+x)+axe-x.

(1)当a=1 时,求曲线y=f(x)在点(0,f(0))处的切线方程;

(2)若f(x)在区间(-1,0),(0,+∞)各恰有一个零点,求a的取值范围.

分析本题以求曲线的切线方程判断函数的零点个数为设问,考查逻辑推理与数学运算等核心素养.第(1)问所求切线方程为y=2x,过程略.第(2)问可直接对参数a分类讨论,并对自变量x分段研究,利用导数判断函数的单调性,借助零点存在性定理判断求解.

解法1(分类讨论)易知f(x)的定义域为(-1,+∞),且

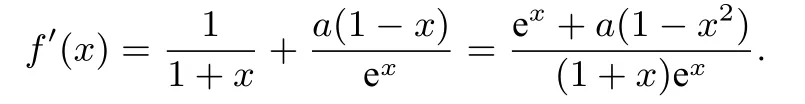
(2)设g(x)=ex+a(1-x2),x ＞-1,则g(0)=a+1,且g′(x)=ex-2ax.

若a ＞0,当x ∈(-1,0)时,g(x)＞0,即f′(x)＞0,可得f(x)在(-1,0)上单调递增,有f(x)＜f(0)=0,则f(x)在(-1,0)上没有零点,不合题意.

若-1 ≤a≤0, 当x ∈(0,+∞)时,g′(x)＞0, 可得g(x)在(0,+∞)上单调递增,有g(x)＞g(0)=1+a≥0,即f′(x)＞0,从而f(x)在(0,+∞)上单调递增,有f(x)＞f(0)=0,故f(x)在(0,+∞)上没有零点,不合题意.

以下考虑a ＜-1 的情形.

①当x ∈(0,+∞)时,g′(x)＞0, 则g(x)在(0,+∞)上单调递增, 而g(0)=1+a ＜0,g(1)=e＞0,存在m ∈(0,1),使得g(m)=0,即f′(m)=0.

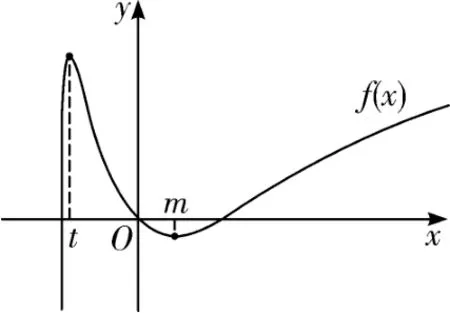
图1

当x ∈(0,m)时,f′(x)＜0, 则f(x)单调递减, 有f(x)＜f(0)=0, 即f(x)没有零点; 当x ∈(m,+∞)时,f′(x)＞0,则f(x)单调递增,且x →+∞时,f(x)→+∞,可知f(x)在(m,+∞)上有唯一零点.从而可得f(x)在(0,+∞)上有唯一零点.

②当x ∈(-1,0)时,设h(x)=g′(x)=ex -2ax,则h′(x)=ex -2a ＞0, 可得g′(x)在(-1,0)单调递增.而g′(-1)=+2a ＜0,g′(0)=1＞0,存在n ∈(-1,0),使得g′(n)=0.

当x ∈(-1,n)时,g′(x)＜0, 则g(x)单调递减; 当x ∈(n,0)时,g′(x)＞0,则g(x)单调递增,有g(x)＜g(0)=1+a ＜0.又g(-1)=＞0, 存在t ∈(-1,n), 使得g(t)=0,即f′(t)=0.

当x ∈(-1,t)时,f(x)单调递增;当x ∈(t,0)时,f(x)单调递减,有f(x)＞f(0)=0.又x →-1 时,f(x)→-∞,则f(x)在(-1,t)上有唯一零点,而(t,0)上无零点,即f(x)在(-1,0)上有唯一零点.

综上,可知a的取值范围为(-∞,-1).

这是一道探究参数对函数零点个数影响的问题,求解关键是对a的范围进行合理分类.在参数a的不同取值范围情况下,解答过程并未对函数f(x)在(-1,0)与(0,+∞)两个区间段中的零点个数进行全面的分析,从而产生以下问题.

问题1当a ＞0 时,f(x)在(0,+∞)上的零点情况如何?

问题2当-1 ≤a≤0 时,f(x)在(-1,0)上的零点情况如何?

先对问题1 进行探讨.

当x ∈(0,1]时,g(x)＞0, 则f(x)单调递增, 可得f(x)＞f(0)=0,即f(x)在(0,1]上无零点.以下讨论f(x)在(1,+∞)上的零点个数.

当x ∈(1,x1)时,g′(x)＜0, 则g(x)单调递减; 当x ∈(x1,+∞)时,g′(x)＞0, 则g(x)单调递增, 有gmin=g(x1)=ex1+a(1)=2ax1+a(1)=a(1+2x1).

当x ∈(1,x2)时,f′(x)＞0,则f(x)单调递增;当x ∈(x2,x3)时,f′(x)＜0, 则f(x)单调递减; 当x ∈(x3,+∞)时,f′(x)＞0,则f(x)单调递增,易知f(x)在(1,x2]上无零点.又则f(x)在(x2,+∞)上无零点, 即f(x)在(1,+∞)上无零点.

综上可知,当a ＞0 时,f(x)在(0,+∞)上无零点.

以上对问题1 的探究用的是分类讨论思想,但用同样的方法探究问题2 时,却很繁杂,无法根据参数a的不同范围得到结果,从而引出另一问题.

问题3例1 有没有别的解法,可以减少或规避对参数a的分类讨论?

问题4对于这类含单参数零点问题的导数题,解法是否具备常规性?

二、其它解法的探究

针对这类含单参数零点问题的导数题,我们一般可以将参数a分离,利用导数研究具体的不含参函数的图象,再讨论它与直线y=a的交点情况(见解法2);还可将该函数零点问题转化为两函数图象的交点问题,利用数形结合来解决(见解法3),以下给出详细解析.

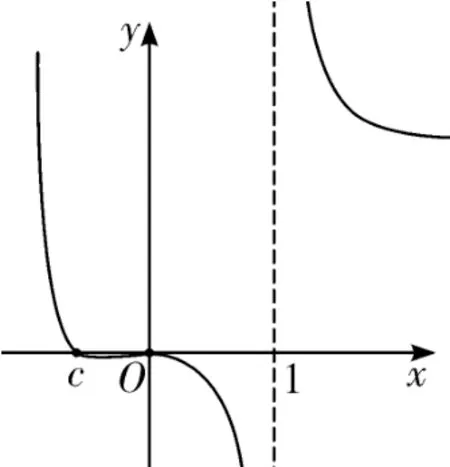
图2

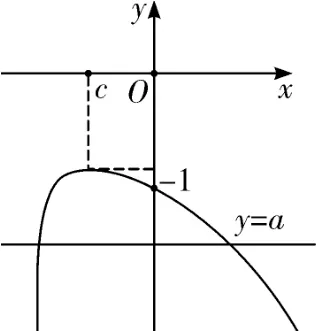
图3

解法3(数形结合)将f(x)=ln(1+x)+axe-x=0,变形为ax=-ex ·ln(1+x), 则问题转化为曲线y=-ex ·ln(1+x)与直线y=ax的交点个数问题, 其中参数a表示直线的斜率.

直线y=ax为过原点的直线,如图4 所示,当直线斜率小于曲线在原点处的切线的斜率,即在l1位置时,满足题意.又F′(0)=-1, 则a ＜-1.

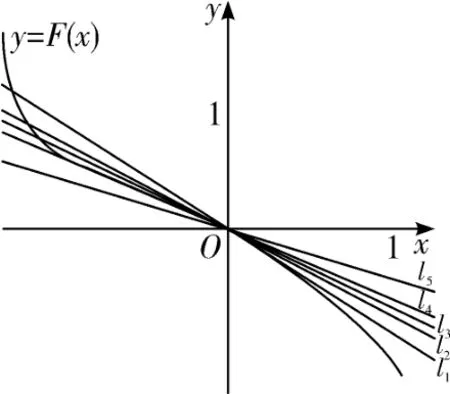
图4

分类讨论思想是高中数学重要的数学思想,特别是对函数单调性的分类讨论是历年高考的必考点,也是我们高考备考中不能回避的问题,思路简单,使用范围广,但有点繁杂;参数分离,可构造不含参数的函数,解题思路清晰,但求导时复杂,而且要用到极限思想;借助参数的几何意义,数形结合求解形象直观,但对函数曲线作图要求很高.以上解法2 与解法3,对于我们来说非常熟悉,不但解决了问题3,而且问题2 与问题1 都迎刃而解,具体过程如下:

由解法2 中函数G(x)的图象(如图3),

问题1 与问题2 也可由解法3 中函数F(x)的图象与过原点的直线y=ax的交点情况来讨论,通过图4 便可得出结论,详细过程留给读者完成.

三、方法拓展

题目1 的求解需对参数a分类讨论,同时也需对自变量x分段讨论,两种讨论的结合对考生的运算与推理能力要求很高,而且经常出现在历年高考导数题中,比如:

题目2(2015年全国I卷理科第21 题)已知函数

(1)当a为何值时,x轴为曲线y=f(x)的切线;

(2)用min{m,n}表示m,n中的最小值,设函数h(x)=min{f(x),g(x)}(x ＞0),讨论h(x)零点的个数.

分析第(1)问从略.第(2)中涉及最值函数, 分类与分段讨论是解决最值函数问题的一个方向.不难发现, 当x ∈(1,+∞)时,g(x)＜0, 则h(x)=min{f(x),g(x)}≤g(x)＜0,即h(x)在(1,+∞)无零点;当x=1 时,g(x)=0,需要结合f(1)的符号讨论;当x ∈(0,1)时,g(x)＞0,则问题转化为讨论f(x)在(0,1)的零点个数.